基于LS-SVM的煤炭建设项目投资估算模型研究

宁 晖

(中煤能源研究院有限责任公司，陕西 西安 710054)

投资估算是在项目决策阶段，以方案设计为依据，按照规定的程序和方法，对拟建项目所需总投资及其构成进行的预测和估计。估算投资作为论证拟建项目的重要经济指标，既是建设项目技术经济评价的基础，又是该项目在实施阶段投资控制的目标值[1-2]。因此，全面准确快速地对建设项目投资进行估算，是科学、客观、有效地进行项目决策的关键。投资估算方法较多，各有其适用的条件和范围，一般可采用的估算方法有简单匡算法和分类详细估算法[1-2]。简单匡算法计算简单、速度快，但估算误差往往较大；分类详细估算需要以详细的工程资料为基础，估算精度高，但涉及专业多，工作量大，耗费时间较多。在项目前期决策阶段，尤其是投资机会研究和初步可行性研究阶段，往往获取的项目信息较少、设计深度不足、工程资料欠缺、时间要求紧迫，无法直接采用详细指标法进行分类估算，但这一阶段的投资估算对企业决策影响较大。为了在项目前期工作中，能够快速、准确估算项目的建设投资，在收集大量投资数据的基础上，本文提出了采用数据挖掘的方法和技术，建立起基于最小二乘支持向量机的投资估算模型。

1 基于最小二乘支持向量机的投资估算模型构建

支持向量机(support vector machine，SVM)是建立在统计学习理论基础之上的新型机器学习方法，专门针对小样本学习问题，以结构风险最小化为原则，在很大程度上克服了传统机器学习方法中的过学习、 非线性、 维数灾难以及局部极小值等问题， 有很强的非线性处理能力和良好的泛化性能，在社会经济的多个领域都获得越来越广泛的研究和应用[3-5]。

1.1 最小二乘支持向量机基本原理

最小二乘支持向量机(least squares support vector machine，LS-SVM)作为SVM的改进和推广，采用误差项的平方，将不等式约束改成等式约束，最终求解线性方程组即可，避免了求解二次规划问题，提高了求解问题的速度和收敛精度[5]。

最小二乘支持向量回归机可表述为式(1)和式(2)优化问题。

(1)

s.t.yi=(w×φ(xi))+b+ξi,i=1,…,l

(2)

式中：w为权向量；b为偏置；ξi为误差项；C>0为正则化参数。为求解上述优化问题，引入Lagrange函数，见式(3)。

(3)

式中，α=(α1,α2,…,αl)T为拉格朗日乘子向量。

根据KKT条件，有式(4)～式(7)。

(4)

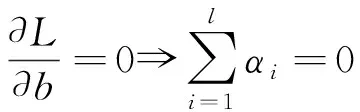
(5)

(6)

(7)

消去变量w和ξi,可得线性方程组，见式(8)。

(8)

式中：1e=[1,1,…,1]T，y=(y1,y2,…yl)T；Il为l×l单位矩阵；K为核矩阵，见式(9)。

(9)

式中：k(xi,xj)=(φ(xi)×φ(xj))；i,j=1,2,…,l。

通过求解方程组，得到最优解α*和b*，进而可以得到最小二乘支持向量机的回归函数，见式(10)。

(10)

在支持向量机算法中，选择合适的核函数是关键的一步，核函数的种类较多，常用的有以下几种。

线性核函数，见式(11)。

k(x,x′)=(x,x′)

(11)

多项式核函数，见式(12)。

k(x,x′)=((x,x′)+1)d

(12)

径向基核函数(radial basis function，RBF)，见式(13)。

k(x,x′)=exp(-σ‖x-x′‖2)

(13)

1.2 算法流程设计

基于回归预测的基本思想，应用最小二乘支持向量机进行项目投资估算的算法包括数据预处理、选择最优参数、训练模型及拟合预测四个步骤，流程如图1所示。

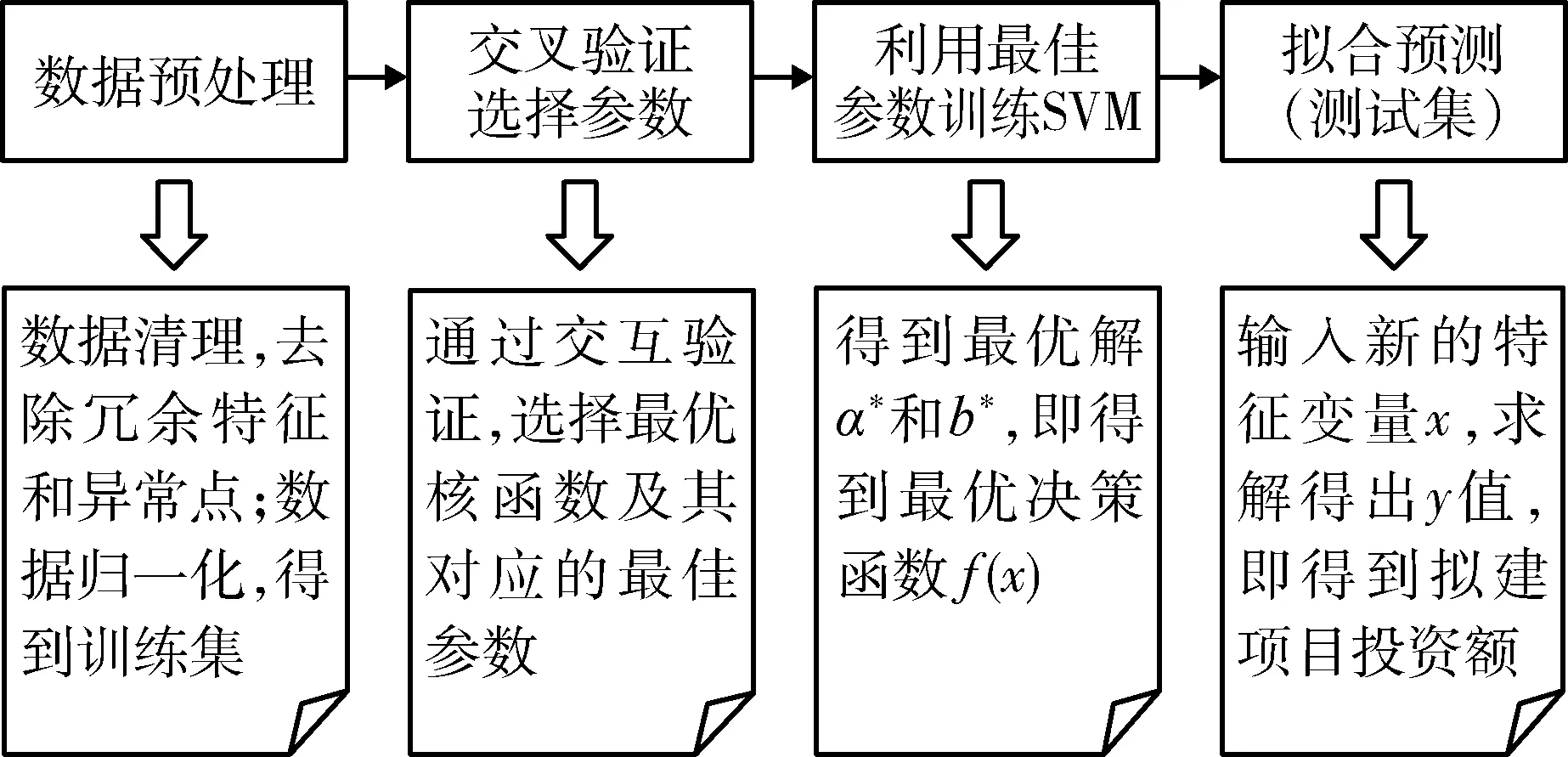
图1 基于LS-SVM的投资估算流程图Fig.1 Flowchart of investment estimationbased on LS-SVM

基于LS-SVM的投资估算算法详细描述如下所述。

第一步：数据预处理。对输入样本集W={(X1,Y1),(X2,Y2),…,(Xm,Ym)}进行数据清洗、数据规约等，消除噪声数据如离群值或重复值等异常点、删除不相关及冗余变量，并对数据进行[0,1]区间归一化，得到数据集D={(x1,y1),(x2,y2),…,(xn,yn)}。

第二步：交叉验证选择参数。将数据集D随机地分成包含l个样本点的训练集Train和包含k个样本点的测试集Test,且l+k=n。

选取线性核或径向基(RBF)核，学习最优的惩罚参数C与RBF核参数σ。

1) forC=2-10,2-9.5,2-9,…,29.5,210；

2) forσ=2-10,2-9.5,2-9,…,29.5,210(注：线性核无此参数循环)；

3) fori=1,…,10；

4) 将训练集Train随机分成10份，以其中9份合在一起建立模型，用剩余一份作为测试，计算出均方根误差等评价指标；

5) End；

6) 计算10组实验均方根误差的平均值；

7) End；

8) End。

比较C和σ所有组赋值下的均方根误差，选择最小值对应的C和σ为最优参数。

为了衡量算法的学习性能，常见的评价回归算法性能的指标有均方根误差(root mean squared error，RMSE)和决定性系数(R2)。 定义见式(14)和式(15)。

(14)

(15)

2 项目样本特征选取

煤炭建设项目的投资受矿山地质条件(资源赋存深度、煤层结构及厚度、顶底板岩性等)、矿井技术条件(采煤方法、开拓方式、采掘工作机械化程度等)、项目厂址条件(交通、供水、供电、原材料供应等)、政策环境条件及价格市场条件等因素的影响[6-7]。不同条件下，投资水平的差异较大。以井工矿为主要研究对象，本文设置的主要特征包括项目地点、项目设计时间、设计生产能力、建设工期、设计阶段、开拓方式、井筒施工方法、采煤方法(工艺)、采煤工作面、瓦斯等级、水文地质类型、煤层埋深、煤层倾角、是否为软岩等主要信息。详细见表1。本文提取特征主要从地质赋存和工艺设计等方面考虑了与投资关联度较高的条件及因素，并且全部信息可以从项目设计文件中提取。在实际预测中，需要做进一步的数值分析，去除无关及冗余特征。

表1 井工矿主要特征表Table 1 Main features of coal mine

续表1

3 数据实验

本文研究的建设投资中剔除了矿权价款、预备费及某些项目特有的费用等，并且矿井配套的铁路专用线、矿井水深度处理或其他特殊工程的投资等均不包含在本次分析范围之内。本文数据实验所有程序在Matlab中编码实现。

3.1 样本收集

本次建模使用的矿井样本数据主要来源于设计文件，包括可行性研究报告及初步设计等，共计45个，其中可研数据31个，初设数据14个。项目所在地区涵盖了陕西省(榆林市、府谷县、咸阳市)、山西省(晋中市、晋城市、太原市)、内蒙古自治区(鄂尔多斯市)、新疆维吾尔自治区(哈密市、塔城市、伊犁哈萨克自治州)、甘肃省、贵州省、云南省、青海省等主要产煤地区；项目设计生产规模主要集中在1.2～15.0 Mt/a范围内；开拓方式以立井和斜井开拓为主。样本具有较强的代表性和较好的学习价值。

3.2 数据预处理

首先，在对所有字符性变量进行数值化处理的基础上，分别绘制了设计生产能力、开拓方式、设计时间和项目地点四个变量与吨煤投资的关系箱体图[8]，如图2所示。由图2可知，不同维度下的投资分布特征，通过观察和对比，初步判断第35个样本点为异常点。其次，对所有变量进行了关联分析，计算了两两变量间的Pearson相关系数[8]，见表2。由表2可知，设计生产能力与吨煤投资关联度最大，为负相关关系；而设计阶段、水文地质类型与建设投资的相关系数均小于0.3，表示关系极弱，认为不相关。最后，对数据进行[0,1]区间归一化，转换函数，见式(16)[9]。

表2 变量相关系数表Table 2 Variable correlation coefficient

图2 主要变量与吨煤投资的关系箱体图Fig.2 Box diagram of the relationship between main variables and tons of coal investment

(16)

3.3 模型建立与预测结果

按照交互验证的方法选择最优参数，将训练样本集合随机分成10份，其中9份合在一起建立模型，用剩余1份作为测试。这样，最小二乘支持向量机在10组不同的训练集和测试集上进行实验，取10次实验的平均结果作为预测结果。

由表3可知，采用线性核函数和RBF核函数的最小二乘支持向量回归机所得的确定性系数R2都超过了0.9，MSE值分别为0.005 0和0.003 3，预测结果良好。但相比较，采用RBF核函数的最小二乘支持向量回归机在井工矿吨煤投资估算上获得了更优的预测精度。

表3 模型最优参数与评价指标结果表Table 3 Model optimal parameters and evaluationindex results

最优参数选定后，利用两种核函数在35个训练样本集上分别进行模型训练，得到各自的最优决策函数，再通过最优决策函数分别对8个测试样本点进行预测，预测结果见表4、图3和图4。

表4 井工矿吨煤投资预测结果Table 4 Forecast results of coal mine investment 单位：元/t

由表4可知，使用RBF核函数的最小二乘支持向量回归机在测试集上预测的最大相对误差为24.43%，不超过投资机会研究阶段投资估算的允许误差率30%[7]；预测相对误差介于10%～20%之间的有两个样本点，分别为17.79%和19.98%，低于初步可行性研究(项目建议书)阶段投资估算的允许误差率20%[7]；其余5个测试样本点的预测相对误差全部小于可行性研究阶段投资估算的允许误差率10%[7]，最小相对误差为1.83%；预测的相对误差平均值为10.95%。

由图3和图4也可以看出，该模型具有较高的预测精度和较强的泛化性能。但相比较，采用RBF核函数的最小二乘支持向量回归机的预测值和真实值具有更好的吻合效果。

图3 线性核函数预测结果Fig.3 Prediction results using linear kernel function

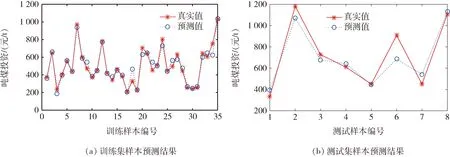
图4 RBF核函数预测结果Fig.4 Prediction results using RBF kernel function

4 实例分析

除了随机数据实验，本文选取了山西省某矿井(2011年9月可研，斜井)、陕西省某矿井(2017年12月可研，斜井)、内蒙古自治区某一矿井(2018年3月初设，立井)、云南省某矿井(2015年9月初设，立井)、内蒙古自治区某二矿井(2012年3月初设，立井)等项目作为拟建项目，假设投资未知，分别用两种核函数的最小二乘支持向量机算法和简单匡算法中的生成能力指数法进行投资预测，结果见表5和图5。

图5 实际项目投资预测对比图Fig.5 Comparison chart of actual project investment forecast

由表5可知，生产能力指数法预测误差较大，对所有项目的投资预测精度均低于最小二乘支持向量回归机算法。 而最小二乘支持向量回归机算法除了对陕西某矿井的投资预测相对误差高于10%以外，对其他项目采用两种核函数预测的相对误差全部小于10%，其中RBF核函数的整体性能优于线性核函数。

表5 实际项目投资预测结果对比表Table 5 Prediction results of actual project investment 单位：元/t

造成以上结果差异的主要原因在于两种方法的预测原理存在本质区别：生产能力指数法预测项目投资时，只与搜寻到的目标项目有关，合适的目标项目是否存在以及其投资是否合理直接影响预测结果的准确性，另外，计算公式中的指数和综合系数的确定受主观经验影响较大；支持向量机算法在去除数据集中异常数据点后，每次预测都会学习数据集中所有样本的特征和投资之间的隐含关系，综合了全部样本信息，另外，模型中的参数以网格搜索的方式寻找最优，强调的是模型的泛化性能。

5 结 论

1) 本文模型技术特征提取简单方便、迅速快捷，避免了分类指标估算时，技术人员详细设计各单体工程技术参数与具体工程量的过程，节省了估算时间，提高了工作效率。

2) 本文模型训练过程科学合理、准确高效，综合了数据集中所有样本数据(去除异常点)的全部信息，避免了依据类似项目进行投资估算时的主观性和偏差性，降低了估算误差。

3) 本文模型具有动态学习的优势，随着新的样本数据不断加入，可以不断优化模型、更新估算投资，进一步提高预测精度。