基于面向对象模糊Petri网的信息物理系统能耗模型

余嘉伟，胡海洋

(杭州电子科技大学 计算机学院，浙江 杭州 310018)

信息物理系统(Cyber-Physical System，CPS)在运行的过程中，计算过程的推进与物理环境的变化形成了多种事件，包括环境感知、指令生成、行为调控等，从而组成一个闭环结构。因此，CPS具备较强的事件驱动性，其连续的物理进程与离散的计算进程之间构成了多种复杂的交互事件[1]。具体地，可将CPS分为三大组件：传感器、控制器、执行器[2]。其中，传感器负责感知并简单处理环境中的信息；控制器负责根据获得的信息拟定和发送指令；执行器负责执行收到的指令，从而改变物理环境。

虚拟世界和现实世界的紧密联系赋予了CPS独特的优越性，使其成为一个实现高度智能化的复杂嵌入式系统，但其能耗分析却成为了瓶颈。CPS的能耗分析是其设计与维护中的关键挑战之一，因为这要求设计者必须考虑到CPS的各个异构组件和它们之间的紧密交互，以及组件内部活动所产生能耗的不确定性。

现阶段，在CPS的能耗分析方面，国内外学者也进行了一些研究。文献[3]通过开发和求解基于随机活动网络的随机模型，分析了铁路道岔加热器CPS系统的可靠性和能耗指标。文献[4]提出了一种基于统计模型检查的环境感知能耗评估框架，该框架中使用随机混合自动机对影响CPS能耗的各种环境因素进行建模。文献[5]扩展了基于微体系结构的时序分析方法，在准确地说明保持设备处于活动状态的执行时间的基础上，提出了用于分析CPS最坏能耗的全系统分析框架。文献[6]提出了一种基于时间状态转换矩阵的CPS软件能耗建模方法，并设计了基于有界模型检验技术的多属性约束能耗分析方法。文献[7]提出了一种基于体系结构能耗建模的CPS软件可信性评估方法，该方法基于能耗时间Petri网建立CPS的能耗模型，并分析了影响CPS软件可信性的能耗问题。文献[8]将CPS软件解构为构件、接口、连接件，随后使用能耗随机Petri网对这些模块进行了建模与能耗预测。

上述研究工作从不同角度提出了对CPS进行能耗分析的各种方法，但还存在着不足之处，主要体现在两方面：(1)多数研究着重点在于CPS的软件构件部分，但缺少对整个CPS(传感器、控制器、执行器)的能耗建模；(2)未考虑CPS在运行过程中各活动能耗的不确定性，这导致分析结果虽较为正确，但却都缺乏一定的精准性，从而无法完全反映CPS的实际能耗。并且，在逐渐普及应用CPS的智能制造领域，目前的应用文献十分缺乏。

基于这些问题，本文构建了一种面向对象模糊Petri网(Object-Oriented Fuzzy Petri Net，OFPN)能耗模型。该模型以面向对象的技术建模CPS的模块化结构，并使用三角模糊数及其α截集的方法表征能耗的不确定性。最后提出了一种CPS组件能耗分析算法，结合输入的变迁模糊能耗值与OFPN的可达标识图，输出一系列解模糊的能耗数值，提高了结果的准确性。

1 OFPN能耗模型

Petri网[9]最早由Carl Adam Petri于1962年提出，它是对离散并行系统的数学表示，并通过资源(托肯)的流动来表示系统的动态变化。Petri网具有严格的数学表达方式与直观的图形表达方式，被广泛应用于建模和分析并发、异步、分布式的系统。在各种建模方法中，Petri网因其兼具的静态与动态特性，已成为制造系统建模与分析的成熟工具[10-11]。Petri网良好的可扩展性使其既能分析制造系统的生产率和设备利用率等性能指标，又可以检查与防止资源冲突和堆栈溢出等消极行为。

然而，传统Petri网存在着诸多不足，例如无法建模CPS中的异构组件之间的交互行为，且无法描述CPS不确定的能耗属性。因此，本文将传统Petri网扩展为面向对象模糊Petri网，作为一种新的CPS能耗分析模型。

1.1 三角模糊数及其α截集

诸如CPS的复杂系统的设计与分析往往涉及到不确定性。在CPS中，这些不确定性主要表现为随机性和模糊性。虽然描述与建模不确定性的主流方法是基于概率的随机模型(例如随机Petri网[12]等)，但这些模型不适用于描述所有的不确定性，只适用于随机性。类似于CPS能耗这种属性的不精确性是由于测量精度有限而导致的，本质上不是统计数据，不能用概率来描述[13]。因此，使用模糊集理论[14]中的模糊数来量化能耗的一维数，是一种可行的解决方案。

三角模糊数[15-16]是最常见的模糊数，与LR型模糊数[17]相比，它的用法较为简便，使用范围更广。

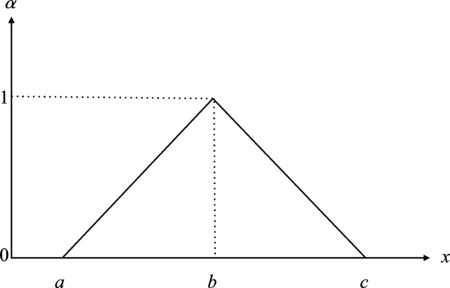
图1 三角模糊数的几何表示

在Petri网中引入三角模糊数的做法，即用三角模糊数量化Petri网中变迁能耗属性的一维数，再将其表示为对应的α截集。由于三角模糊数的α截集并非实数形式的数值结果，因此利用三角模糊数的运算法则[18]得到最终能耗计算结果的模糊值时，需将其进行解模糊。具体方法是，求得模糊能耗值即α截集后，由于三角模糊数在α=1处的截集取得唯一值(最可能值)；在α=0处的截集取得两个边界值(最小、最大值)。因此，以0、1分别代入一个三角模糊数的α截集，即可解模糊得到该模糊数的最小值、最大值和最可能值。

1.2 OFPN网系统

为了阐述基于OFPN的CPS能耗建模过程，下面首先给出OFPN网系统的正式定义。

OFPN网系统定义为一个二元组ONS=。其中，Ob是系统中的对象集合，R是系统中对象之间的消息传递关系的集合，二者的详细定义如下。

信息发送者对象Obi至信息接收者对象Obj之间的消息传递关系Rij∈R定义为一个七元组Rij={OMi,gij,IMj,Iij,Oij,Cij}。其中，OMi是对象Obi的输出信息库所的有限集合；gij是Obi到Obj的信息传递的门变迁的有限集合；IMj是对象Obj的输入信息库所的有限集合；Iij(OMi,gij)是从输出信息库所OMi到门gij的输入映射(函数)；Oij(gij,IMj)是从门gij到输入信息库所IMj的输出映射(函数)；Cij={C(IMj),C(OMi)}是输入、输出信息库所中托肯的色彩集合，且有Cij∈C。

OFPN网系统是一个两层结构模型，如图2所示。其中，系统层描述了CPS的整体结构与组件间的交互，由消息传递关系R定义；组件层描述了CPS传感器、控制器、执行器的内部活动，由对象的OFPN模型Ob定义。

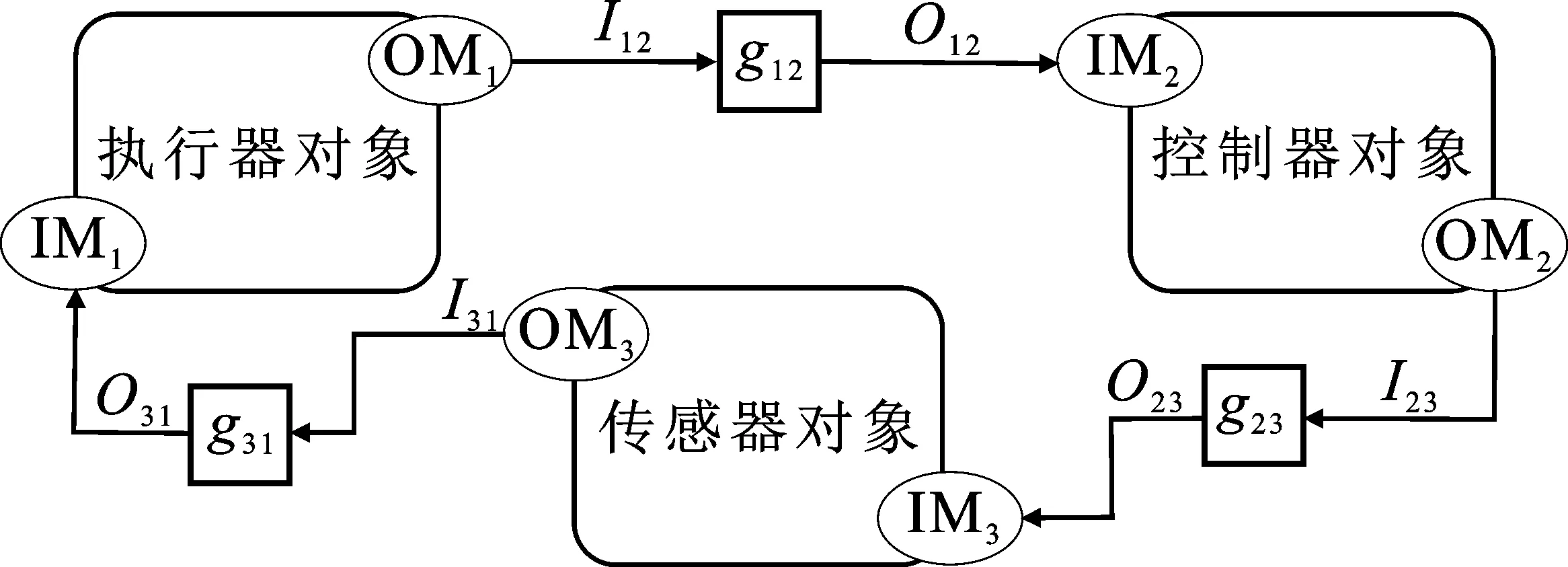
图2 OFPN网系统

为了定义OFPN的发生规则，使其的动态行为符合CPS的特性，可将OFPN网系统中的所有弧Fij关联一个表达式EXPij∈EXP，且有EXP=EXPI∪EXPO，EXPI∩EXPO=Ø。其中，EXPI表示库所到变迁的弧的表达式，EXPO表示变迁到库所的弧的表达式。则OFPN的发生规则可由式(1)～式(4)给出。

(1)

(2)

(3)

(4)

其中，式(1)表示输入库所为Pi的变迁Tj的发生条件，是当且仅当Pi中托肯的颜色与C(Pi)相同且为资源类托肯时，才满足弧Fij的表达式，从而托肯方可通过Fij流动至Tj将其变为使能(可发生)状态。式(2)为输入库所是信息库所时的特殊情况。式(3)表示Tj发生完成后，托肯被修改为资源类且其色彩被修改为C(Pi)，随后通过Fij流动至输出库所Pj。类似地，式(4)为输出库所是信息库所时的特殊情况。

基于CPS的结构以及OFPN的相关定义，使用OFPN建模CPS及其能耗的过程可分为3步：(1)将CPS中的所有设备归类至传感器、控制器、执行器三大组件；(2)根据组件对象具体数量建立如图2所示的OFPN网系统；(3)根据OFPN中对象的定义与CPS的实际情境，扩展网系统中的对象。

2 CPS的能耗分析

基于OPFN的可达标识图，可进行CPS的能耗分析。OFPN的标识定义为一个一维向量S，且有|S|=|P|+|IM|+|OM|，其中的每个元素是一个表示对应库所中的托肯数目的自然数。S0为初始标识，表示初始状态下的托肯分布情况。由OFPN的发生规则(式(1)～式(4))可知，变迁的发生会导致标识的变化，所以从初始标识开始，可将两个标识之间用以变迁标注的有向箭头连接，得到OFPN的可达标识图。

可达标识图给出了OFPN的全部可能所处的状态以及它们之间的联系(变迁)，使用Petri网分析软件(如PIPE)进行仿真后可得到OFPN的可达标识图。在此基础上，可进行如下所示的组件能耗分析算法。该算法统计分析CPS中各组件产生的能耗的模糊值并进行解模糊，然后将它们的最小值与最大值作为输出。

步骤1为了统计CPS的各组件能耗，需得到OFPN的所有可能执行轨迹，即在OFPN可达图G中找出所有以S0为起(终)点的环路，并存储为σ；

步骤2对σ中的每一个环σi，以S0为起点，将造成标识改变的当前变迁T的能耗模糊值(即α截集e(α))根据其类别(传感器ES(α)、控制器EC(α)、执行器EA(α))累加到当前环σi对应的能耗Ei中，直到再次回到S0；

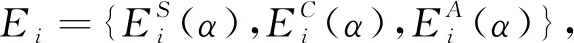
3 实例建模与分析

以杭州西奥电梯有限公司(www.xiolift.com)的智能厚板生产线为例，说明本文所提出方法的详细执行步骤。该CPS包括以下组件：(1)传感器，包括一个测长度传感器，一台工业相机；(2)控制器，包括3个西门子S7-300型号的可编程逻辑控制器(Programmable Logic Controller，PLC)和1个OPC(OLE for Process Control)服务器；(3)执行器，包括一台村田机械M2048TS型号的冲床以及配合工作的机器人(型号为ABB的IRB-6700)、两台LVD折弯机(型号分别为PPEB-220T和PPEC-220T)以及配合工作的机器人(型号为ABB的IRB-6700)、一个码垛机器人(型号为ABB的IRB-6700)。其中部分设备如图3所示。

图3 厚板生产线部分设备

智能厚板生产线生产线负责加工成套的XOA4040KZD999型板(以下简称A型板)和XOA4288BBT989型板(以下简称B型板)，该CPS的具体工作过程如下：

步骤1冲床与其机器人将A型板打孔，同时PPEB-220T折弯机与其机器人折弯B型板；

步骤2B型板折弯完成后，PPEB-220T折弯机与其机器人开始折弯A型板。同时，测长度传感器和工业相机将分别测量折弯完成的B型板的长度和角度，并将检测数据发送至OPC服务器。如果角度不在符合质量要求的正确范围内，则服务器将操作命令发送到PPEC-220T折弯机与其机器人的PLC来根据偏差进行角度校准，否则进行下一步；

步骤3码垛机器人将折弯完成的一块A型板和一块B型板码垛为一组成品。然后，该生产线将从第一步开始重复迭代，以加工后续板材。

在建立了图2所示的OFPN顶层模型后，根据每个组件对象的任务和工作过程，可以将厚板生产线的OFPN网系统模型扩展为如图4所示架构，模型中库所与变迁的详细含义在表1中给出。

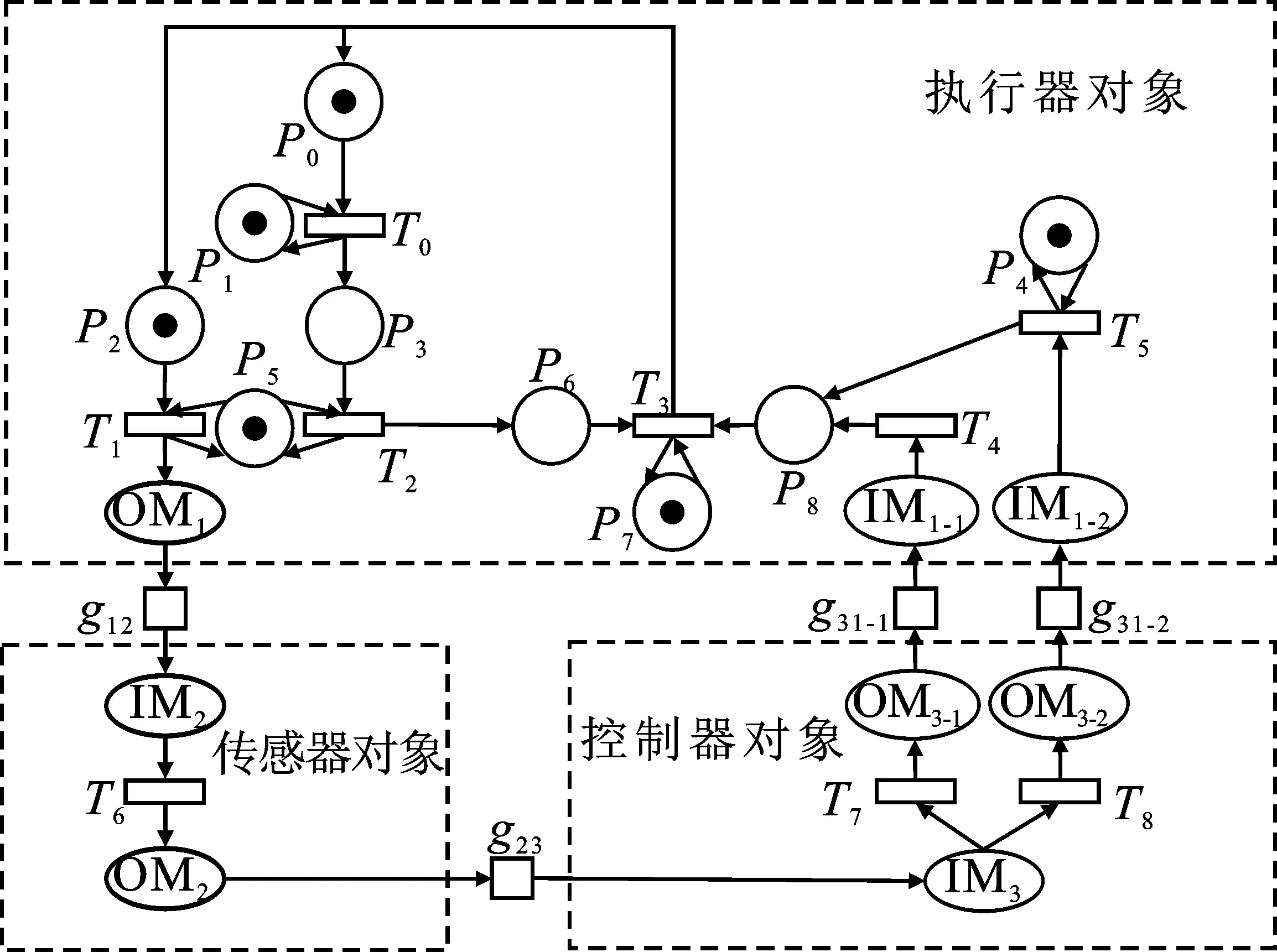
图4 厚板生产线的OFPN网系统模型

在查阅了西奥电梯有限公司的生产数据，并对智能厚板生产线中设备的能耗进行了一系列的实地测量，以及对控制器软件的能耗进行测量[19]后，可得到各步骤能耗的平均值及其波动范围，作为三角模糊数的最可能值以及模糊系数δ的取值依据。然后，根据三角模糊数的α截集方法，将厚板生产线中活动的能耗平均值进行模糊化，作为OFPN中变迁的能耗属性值。最后根据变迁的所属对象进行能耗分类，得到的结果如表2所示。其中，执行器能耗的单位为千瓦时(kW·h)，传感器能耗的单位为焦(J)，控制器能耗的单位为毫焦(mJ，1 mJ=0.001 J)。

本文需要注意OFPN模型中的变迁T4作为逻辑变迁存在，表示“B型板准备码垛”，而非某耗能活动，故其能耗不参与计算。表2中的各变迁的模糊数及其α截集表示形式可由e={0.074,0.663,0.221,0.008,0.116,25.600,0.700,0.700}及δ={0.025,0.087,0.029,0.001,0.018,1.800,0.010,0.010}导出。

对于CPS的能耗分析，根据图4所示的智能厚板生产线的OFPN模型，利用Petri网分析软件PIPE对其进行测试后，发现此OFPN是有界、安全且无死锁的，接着生成其对应的可达图，如图5所示。其中，每一个状态S代表此OFPN的一个标识，以矩形表示S0为初始状态(标识)，以椭圆表示的为中间状态(标识)。

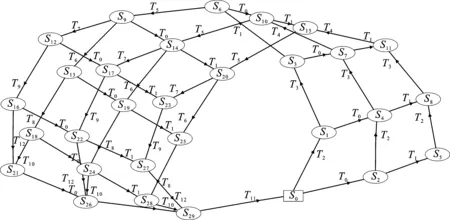
图5 OFPN的可达图

根据本文提出的基于标识的分组件能耗算法，可分别计算出传感器、控制器、执行器能耗的最小、最大以及最可能值，得到的结果如图6和图7所示。

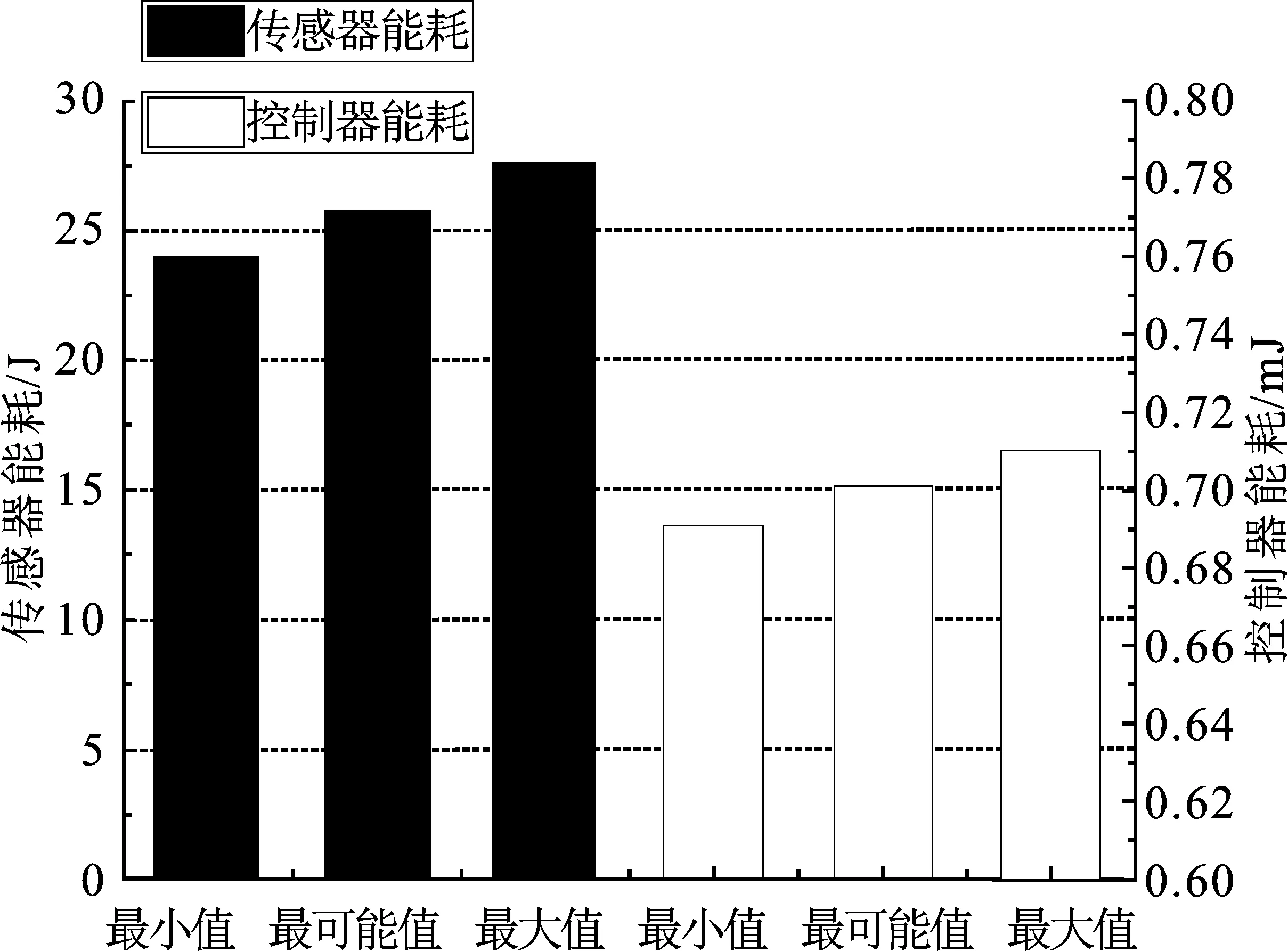
图6 传感器、控制器能耗

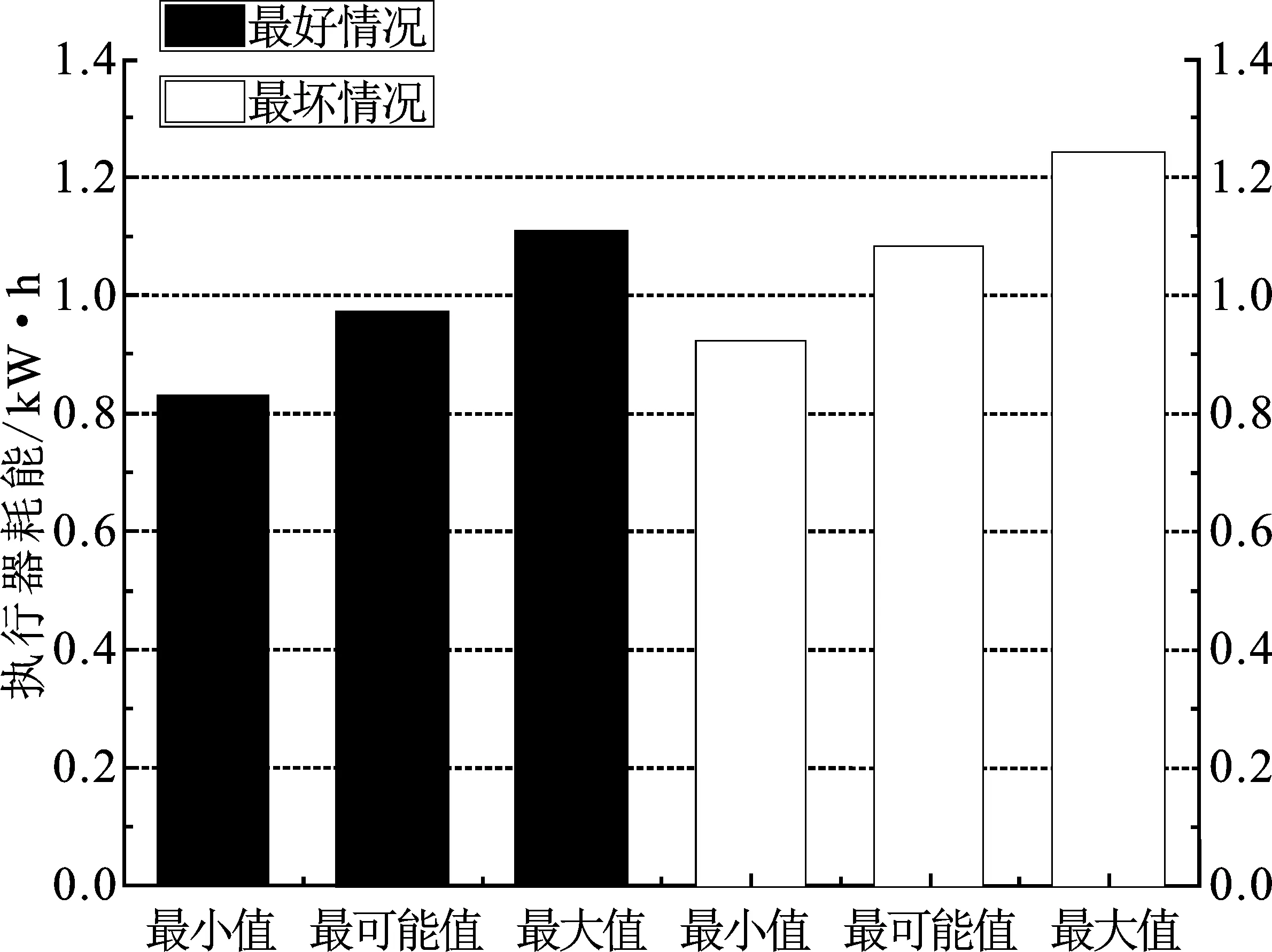
图7 执行器能耗

从图6中可以发现，传感器、控制器的能耗虽存在小幅波动范围，但相对较为稳定。而图7中执行器的能耗分为最好情况和最坏情况，两种情况分别又存在小幅度的波动范围。其原因是B型板在加工过程的中途折弯后，可能会被检测为角度不合格板材，这时就产生了PPEC-220T折弯机和机器人对其进行角度校准的额外能耗。

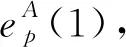
4 结束语

针对CPS组件化的特点，本文提出了一种新的CPS能耗模型面向对象模糊Petri网。在此模型中，CPS的各组件以及组件间的交互被建模为若干个对象以及对象间的通信，而CPS中能耗的不确定性则由模糊数学相关理论予以解决。得到能耗的模糊值并解模糊后，计算结果符合实际情况，进一步验证了本文所提出的模型的有效性，为系统的长期运行与结构调整、流程优化提供了基础。为了提高OFPN的精确度与实用性，在后续的研究中，应当考虑CPS中设备的故障和其他外界因素对能耗的影响，在时间等属性上扩展模型，并在其他领域的CPS进行应用。