循环荷载下CFRP-混凝土界面黏结-滑移模型研究进展

王富羚，王玉田，姜乐乐

(青岛理工大学 土木工程学院，青岛 266033)

提高混凝土结构工程的服役寿命是最有效的节能减排，对混凝土结构进行加固则是延长结构服役寿命的一种方式.近年来，通过碳纤维增强复合材料(Carbon Fiber Reinforced Polymer，简称CFRP)来加固混凝土结构在加固领域得到广泛应用.CFRP加固技术是通过界面黏结应力来实现混凝土与CFRP之间荷载的传递，从而提高混凝土结构的承载能力，界面的黏结性能直接影响CFRP与混凝土之间应力传递的有效性.

一个正常的钢筋混凝土桥面在120年的寿命中可能经历大约7×108次循环荷载[1]，在其服役期间，加固结构破坏形式通常是沿界面发生剥离破坏，破坏前无明显征兆，且循环荷载下的界面破坏时的荷载往往低于静载下的极限荷载.国内外许多学者对循环荷载下CFRP-混凝土界面性能展开了研究，这些研究提高了对CFRP与混凝土界面破坏机理的认识与理解，为今后开展此方面的研究和完善相关理论提供参考.

1 静载下的CFRP-混凝土界面黏结-滑移关系

为了更好地了解界面的黏结机理，许多研究人员对静载作用下CFRP与混凝土界面的黏结-滑移性能进行了系统的研究，包括力学试验、解析分析和数值分析，建立了在高温、干湿循环、冻融循环等不同工况下的CFRP-混凝土界面静载下的黏结-滑移模型.

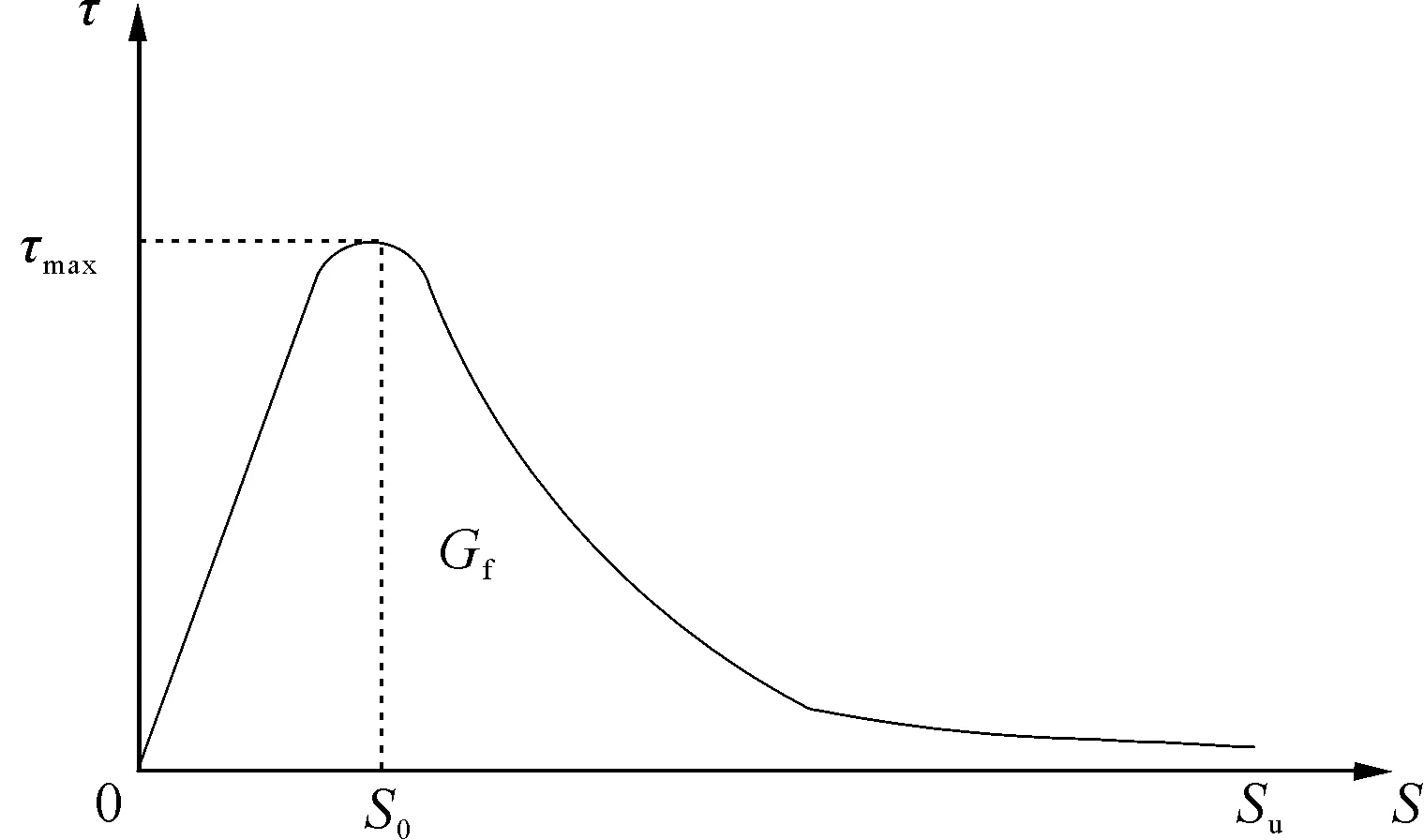
图1 静载下CFRP-混凝土界面黏结-滑移本构模型

然而，以上模型[4-7]只考虑了静载下的影响因素，不能很好地预测循环荷载下黏结-滑移模型的疲劳退化行为.因此，不少研究人员对循环荷载下的黏结-滑移关系展开了一系列研究.

2 循环荷载下的CFRP-混凝土界面黏结-滑移关系

HARAJLI[10]关于钢筋与混凝土界面黏结-滑移模型的研究表明，循环荷载作用下钢筋混凝土黏结-滑移的外部包络曲线与静力加载下的黏结-滑移曲线相近，MORITA等[11]的试验结果说明在不考虑包络曲线的疲劳退化时，循环荷载下的包络线可以近似地看作是静力加载下的黏结-滑移曲线，由此许多研究人员在研究循环荷载下CFRP-混凝土界面黏结-滑移关系时，都是基于静载下的黏结-滑移关系曲线为包络线展开的.

2.1 基于Popovics模型的循环荷载下黏结-滑移关系

图2为KO等[12]提出的以式(1)所示的Popovics模型为包络曲线的循环荷载作用下CFRP片材与混凝土界面的黏结-滑移模型，该模型虽考虑了7个经验参数：最大黏结剪应力τmax及其对应的局部滑移S0、界面断裂能Gf、曲线特征常数a、摩擦应力τfp、负摩擦应力τfn和卸载刚度ki，但没有考虑循环次数对界面损伤的影响，导致模型计算的部分结果与试验结果有差距.

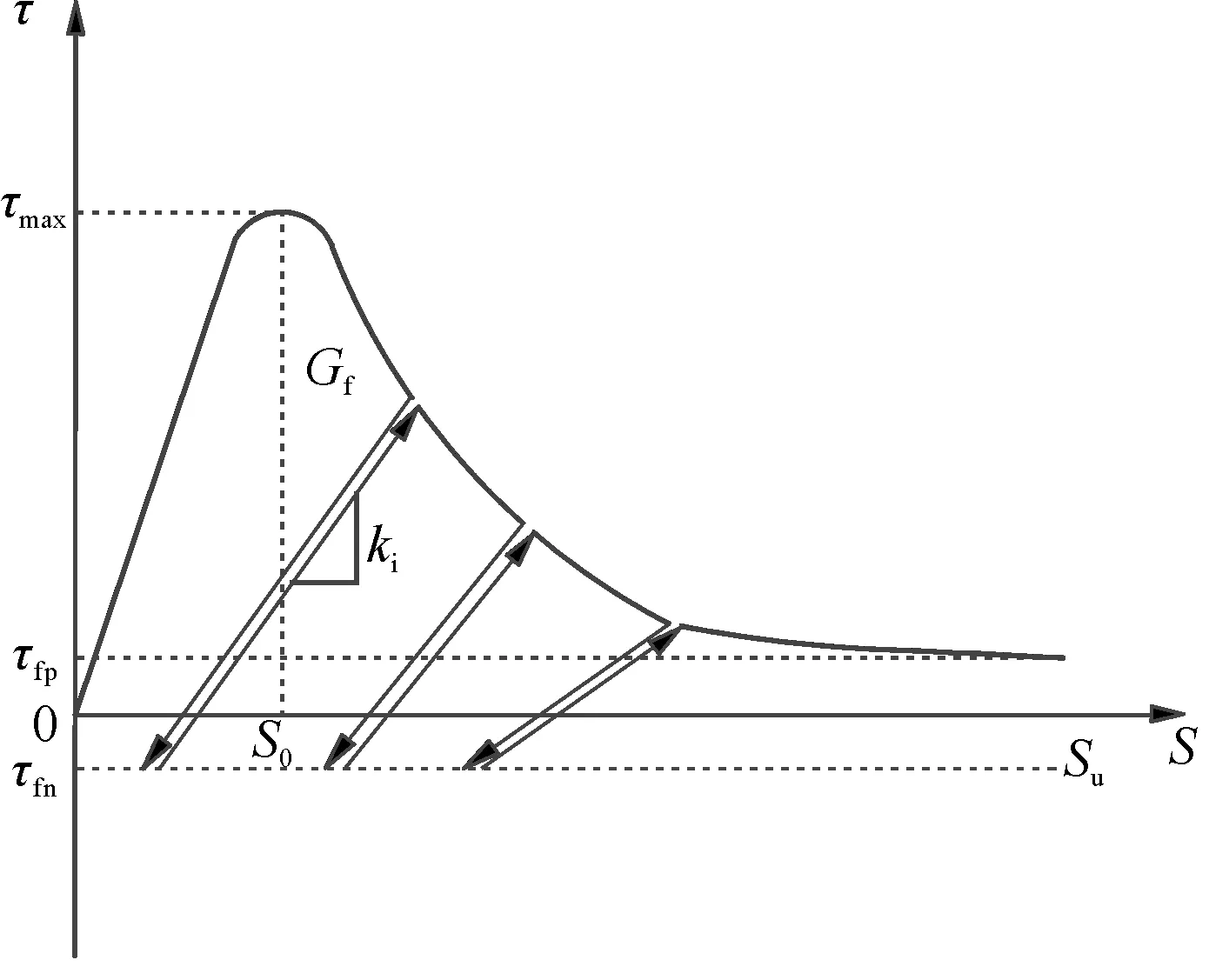
图2 黏结-滑移关系的循环滞后模型

(1)

ZHANG[13]在式(1)的基础上推导出了残余滑移公式，来探究循环荷载下的黏结-滑移关系.式(2)、式(3)表示的模型由经验参数卸载刚度ki定义.疲劳载荷下的局部黏结应力-滑移关系可以用包络曲线上的某一点和卸载刚度来表征，但其未考虑循环荷载的应力比和应力水平对界面损伤退化的影响.

S=0.046e0.26lgN

(2)

(3)

式中：k1为第1次循环的卸载刚度；ki为第i次循环的卸载刚度；N为疲劳循环次数.

2.2 基于双线性模型的循环荷载下黏结-滑移关系

LOO等[14]基于YUN[15]和DAI[16]等的试验数据，以双线性模型为包络线，获得了图3所示的循环荷载下的黏结-滑移本构关系退化模型，模型在循环次数为Nf时失效.式(4)、式(5)中参数通过大量试验数据拟合获得，从而建立了循环荷载下有效黏结-滑移本构关系.

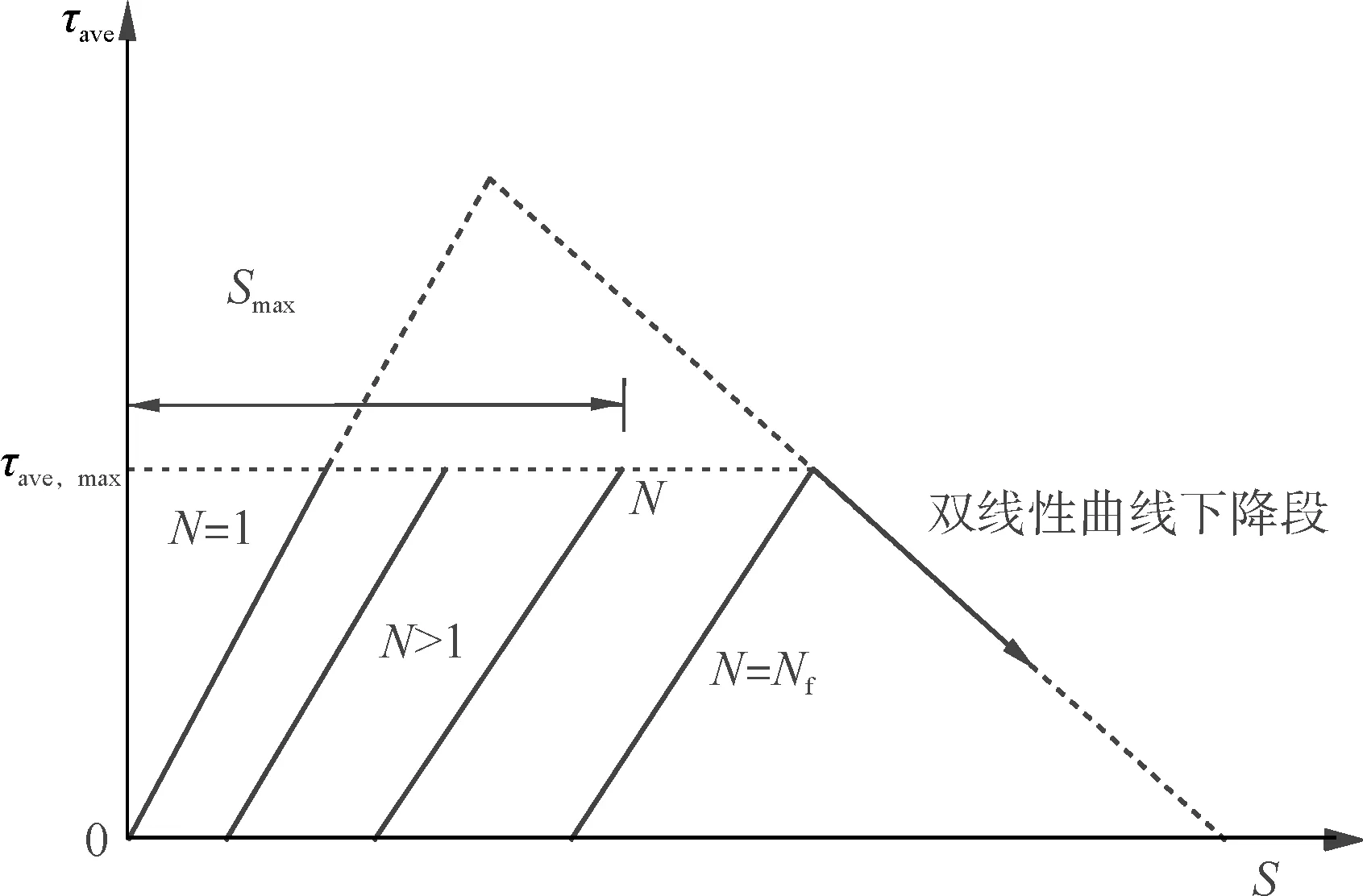
图3 循环荷载下双线性简化黏结-滑移模型

(4)

(5)

式中：Smax为τave,max对应的滑移量；τave,max为静载下失效时平均黏结应力；Eb0为第1次循环的系数；Eb为第N次循环的系数；Δτave为平均黏结应力范围；Δτave，f为失效时平均黏结应力范围；a,b,c,α,β,γ均为利用试验数据回归分析拟合得到的参数.

ZHU等[17]基于式(6)的陆新征双线性模型[18]，建立了循环荷载作用下考虑混凝土强度和疲劳荷载幅值影响的CFRP-混凝土界面非线性黏结-滑移模型，见式(7)—(9).在对疲劳试验结果进行回归分析的基础上，推导出计算疲劳荷载作用下CFRP-混凝土界面最大剪应力的公式，由于该模型是基于有限的试验数据提出的，其准确性有待进一步研究.

(6)

(7)

(8)

(9)

式中：γ为混凝土强度修正系数；T为荷载幅值(Pmax-Pmin)与静载极限承载力Pu之比；Su为黏结剪应力降为零时的局部滑移；βw为宽度修正系数；bf，bc分别为CFRP片材宽度和混凝土试块宽度.

式(10)、式(11)为LI等[19]在陆新征双线性模型基础上建立循环荷载作用下CFRP-混凝土界面黏结-滑移的双线性模型，最大剪应力是准确表达CFRP-混凝土界面剪应力与滑移关系的关键因素，所以通过考虑循环荷载水平Sc、混凝土强度fcu及CFRP片材与混凝土宽度比bf/bc对最大剪应力τft的影响，得出黏结-滑移曲线上升段的斜率kft随循环次数N的退化规律：在循环荷载作用下，黏结-滑移曲线上升段的斜率随循环荷载水平、CFRP片材与混凝土宽度比的增大而增大，随混凝土强度的增大而减小.

τft=kftS0

(10)

(11)

式中：τft为最大剪应力，随荷载循环次数而变化；kft为随循环次数N变化的黏结-滑移曲线上升段的斜率；S0为最大剪应力对应的滑移值；k0为初始加载时黏结-滑移曲线上升段的斜率；c,b为参数，可由Sc，fcu，bf/bc计算得出.

2.3 基于断裂力学的循环荷载下黏结-滑移关系

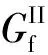
(12)

式中：kE为黏结-滑移曲线上升段的切向黏结刚度；Se=τ0/kE，表示弹性滑移值；τ0为剪切强度；β为黏结-滑移曲线下降段指数参数.

韩强[21]采用静载下界面黏结-滑移曲线代替循环荷载下黏结-滑移曲线的外部包络线，并通过试验获得的退化规律，给出了式(13)界面黏结刚度损伤模型.

(13)

式中：DB为界面黏结刚度损伤变量；ad为黏结退化系数，由试验数据拟合得到；ΔS为剥离前残余滑移量与循环次数的比值.

CARRARA等[22]提出2个损伤变量分别控制界面的强度损失Dτ和刚度损失DK.该模型只需要计算4个独立参数，即3个定义静载II型界面规律的参数和1个定义疲劳行为的独立参数，但模型十分复杂，模型中的参数难以确定.

2.4 基于ABAQUS的循环荷载下黏结-滑移关系

DAUD等[23]利用ABAQUS建立了CFRP-混凝土的有限元模型，模拟了CFRP-混凝土在单剪拉拔试验中的受力性能.利用验证后的模型进行了参数研究，考察了FRP刚度、黏结宽度比和混凝土抗压强度对黏结效果(剥离应变εfe和有效黏结长度le)的影响，并提出了式(14)、式(15)所示的预测CFRP板单剪剥离应变的简单模型.

(14)

(15)

式中：C1—C8为使用Wolfram Mathematica 7软件进行非线性回归计算得到的系数；Ef，tf分别为CFRP片材的弹性模量和厚度.

将结果用于评估各种现有的预测FRP-混凝土黏结性能的设计规范方法，结果表明现有的设计规范都存在明显的差异，缺少统一的设计规范.

3 CFRP-混凝土界面破坏演化过程

图4为黄昆泓[24]基于循环荷载下CFRP-混凝土界面黏结-滑移关系曲线的演化规律，总结出的循环荷载下界面黏结-滑移本构模型的滞回规律：

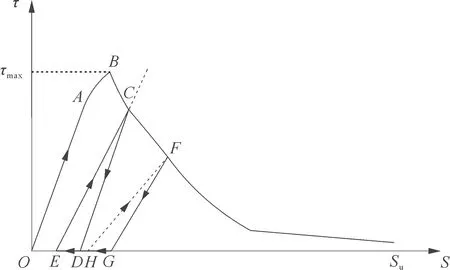
图4 理想状态下循环荷载下黏结-滑移本构模型

1) 在界面黏结剪应力没有达到最大剪应力τmax之前，黏结-滑移曲线上升段接近于直线，加载和卸载路径均与静载下黏结-滑移曲线的上升段(初始刚度)近似；

2) 在界面滑移量超过S0后，OABC为加载路径，CDE为卸载路径，此时已经有疲劳损伤，所以界面此时有OE段的残余滑移量；

3)ECF为下一次循环的加载路线，FGH为卸载路线，EH为此次循环的残余滑移量，则OH为界面总滑移量；

4) 在经历N次循环加载以后，当界面总滑移量大于Su时，界面则发生剥离破坏.

4 结束语

近年来，国内外关于循环荷载下CFRP-混凝土界面黏结-滑移模型的研究得到了长足发展，成果丰硕，但由于CFRP-混凝土界面疲劳试验没有统一的标准，同时各个研究人员处理试验结果方式也不同，导致不同学者之间的试验结果可比性差，结合现有黏结-滑移模型研究进展来看，以下方面有待进一步深入研究：

1) 制定统一的界面疲劳试验标准，准确揭示循环荷载作用下CFRP-混凝土界面黏结-滑移机理；

2) 探明循环荷载的应力比以及应力水平对界面退化的影响规律，建立准确适用的界面刚度损伤退化模型；

3) 提出循环荷载下CFRP加固混凝土的破坏准则，建立统一的疲劳设计方法.