某型直升机机载发射架梁体断裂疲劳分析

刘 越，余文成

(1.北京机电工程研究所，北京 100074；2.北京特种机械研究所，北京 100143)

0 引言

直升机机载发射架(装置)用于武器的悬挂和发射。因直升机挂载能力及飞行任务需求，设计中对发射架尺寸、重量均有严格的要求。发射架多采用铝合金材料作为发射架本体及导轨基材，以实现轻量化设计。但设计中的载荷预估不准确、细节设计不合理等情况，会导致应用的铝合金等轻质材料出现强度及疲劳问题。

1 问题由来

发射架在载机上的带飞疲劳寿命、可靠性指标等研制要求，均在地面环境试验中进行考核。在长时间振动试验中，如果产品结构不尽合理，被考核产品在寿命期内会发生提前断裂现象。本型发射架在进行直升机条件的垂向耐久振动挂载弹体状态试验时，梁体便出现了疲劳断裂问题，如图1。

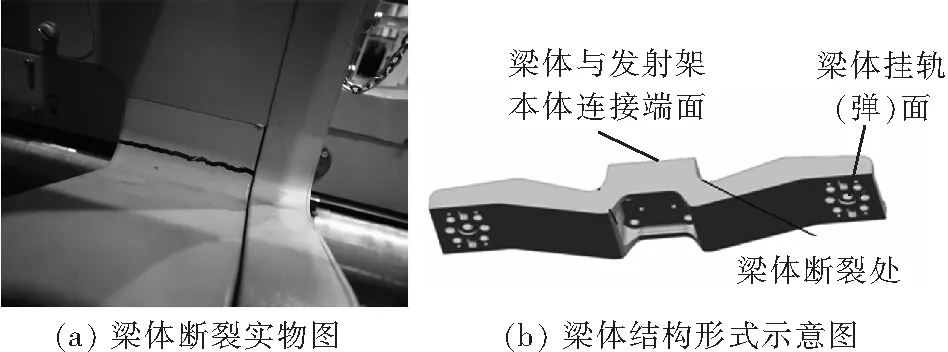
图1 梁体断裂图

对断裂的梁体进行了断口金属金相分析。如图2所示，500倍断口图晶界未见粗化，也没有见到复熔三角现象，无过热过烧现象；100倍断口形貌可见明显撕裂岭存在；50倍断口可见到韧窝存在，是典型的韧性断裂特征，依此判定为疲劳断裂情形。

图2 梁体断口金属金相放大图片

2 机理及分析方法

2.1 疲劳断裂原因

在振动试验中，影响装备结构寿命的主要因素有材料、材料缺陷、振动产生的循环载荷、振动时间的长短等。材料在振动中应力幅或者应力范围是影响结构疲劳的决定因素，振动时间对应的应力循环周期数不断累加也对结构疲劳寿命产生直接影响。

铝合金、高强度钢之类不存在应变时效硬化的材料，理论上没有疲劳极限，随着疲劳循环数逐渐增加，材料的应力幅

σ

连续降低。预计当达到一定循环周时，铝合金材料将出现结构到寿现象，即发生疲劳断裂。

疲劳大概率出现于结构应力集中点、载荷循环交变频繁处、两刚性结构振动接触点等位置。结合本次问题，应力集中点和载荷循环交变频繁导致的疲劳问题不能排除。

2.2 疲劳评定方法综述及选取

2.2.1 评定方法综述

随机载荷疲劳分析方法主要有3种：第一种是基于统计计数的应力时域分析方法；第二种是基于功率谱密度的频域分析方法；第三种是基于有限元的功率谱分析方法。应力时域分析方法首先通过结构分析或实际测量得到结构危险点的应力(应变随时间的变化关系)；采用适当的计数方法，得出不同应力(应变)水平的幅值和均值的分布情况；然后选择适用的损伤累计准则及破坏判据，进行疲劳分析寿命估算。频域分析方法是通过有限元分析或实际测量得到结构危险点的应力功率谱密度，然后利用统计原理获得相应功率谱的相关统计参数，结合应力幅值的概率密度函数，选取适用的损伤累积准则及破坏判据，进行疲劳及寿命预估。基于有限元的功率谱密度分析方法是对装备实体进行有限元建模，在模型中获得结构模态，对振动输入点加载振动试验(随机或正弦激励)条件，获得结构的动力学应力等参数，与材料性能对比，判定结构疲劳的裕度。

2.2.2 评定方法选取

在早前的专项分析中，以有限元功率谱密度分析结构疲劳。虽然模型体现了结构的模态振型等相关参数，在结构振动输入点加载了随机振动密度谱，但由于直升机振动条件固有的随机+正弦耦合振动条件，有限元功率谱分析无法实现耦合振动条件设置，获得的结果只是随机或正弦振动条件下的结构疲劳结果。以文献[3]为代表的机载导轨疲劳寿命预估中，多采用频域分析方法对产品寿命进行预估。但分析中要求随机振动是稳定的，随机振动激励基本符合高斯分布，结构响应也是稳定的随机过程。对于直升机机载发射架振动试验，由于试验条件必须耦合主桨频率(正弦激励)、主桨倍频及叠加随机振动，发射架结构在正弦频域区出现明显响应和功率谱密度幅值，如图3。针对本文研究对象，在设定模型计算条件时，随机叠加正弦振动条件中难以在均匀区间内设定功率谱密度。另外，在发射架悬挂约束点进行功率谱输入，在考虑结构间非线性接触等实际工况、结构阻尼、危险点功率谱密度实值以及确定相关疲劳参数时，模型参数设置存在不确定性或较宽限的选取范围，危险点的疲劳寿命估算可能存在一定偏差。

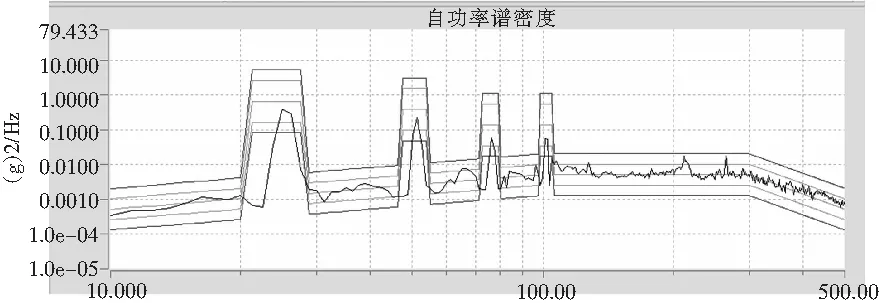
图3 随机加正弦振动条件发射架典型结构测点响应功率谱密度图

应力时域法通过试验获得振动载荷产生的结构应力交变，提取结构的单轴应力参数，等代为结构的时域载荷谱。采用时域载荷中交变中雨流计数获得应力范围和平均应力，以确认载荷循环交变密度及循环次数；使用单轴应力S-N曲线计算疲劳损伤，计算累积损伤获得预估寿命等结果。对于本次发射架寿命预估问题，在实现了导轨结构体振动条件中载荷的测量，记录信号的雨流循环计数可统计后，回归到应力循环损伤累计法开展研究工作，可更准确、直接地得到随机+正弦耦合振动导致的累积结构损伤，从而获得较精确的疲劳预估结果。

3 评定结果

3.1 梁体结构静强度分析

梁体原材料为铝板2024-T351，抗拉强度应为390MPa。经测试硬度，硬度值为HB110～120，对应的抗拉强度约为380～400MPa。

对发射架整体及梁体局部进行静力分析，应力云图如图4、图5所示。经分析，最大应力115MPa，位于梁体下面的5mm薄壁立面处；而在梁体圆弧面交界断裂处应力为53MPa ～60MPa，应力并不大。按静强度理论，铝2024的屈服强度为265MPa，安全系数

n

=265/115=2.3，梁体静强度满足直升机飞行的过载条件。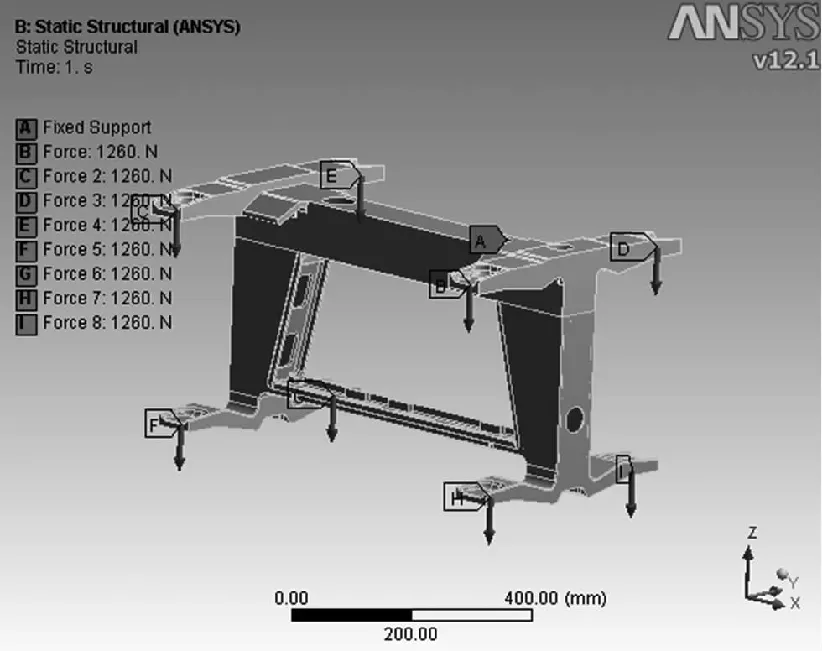

图4 发射架整体静力分析

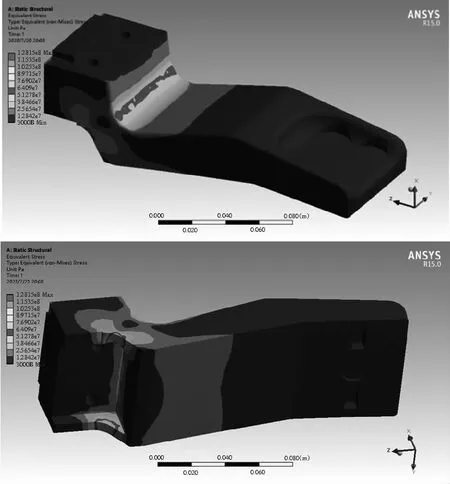
图5 发射架梁体(对称本体)局部静力分析

3.2 疲劳分析

3.2.1 应变测量

按2.2.2节提出的应力时域法，开展本次问题的分析工作，以明析梁体疲劳问题的机理，验证应力时域法应用的有效性。

选用试验室应变测量设备开展结构应变测量。应变测量在结构受迫振动中随载荷变化产生结构应变幅值。参考文献[4]确定，低应变范围内，6系列(常规)铝合金为不敏感的材料，应变率对6系列(常规)铝合金材料力学性能影响不大，可以通过应变采样等代为应力幅值，同时认为对于延性金属的铝合金弹性应变与应力载荷是线性对应的。依此，铝合金2024-T351采用应变测量获得应力幅值是合理的。

试验准备中，在梁体圆弧交界位置侧壁结构上粘贴应变传感器，以测量振动条件中结构的垂向应变。在试验第一步，对梁体进行静载条件的应变标校，以确定梁体应变片对应位置的立壁应变幅值与所受载荷的对应关系。在振动试验开始时，按试验时间记录应变数据，采样频率1000Hz。

3.2.2 振动试验条件

试验台振动采用平均控制方式，振动方向为垂向，宽带随机+正弦。输入综合均方根1.845g加载振动量级。发射架前后挂点处的传感器控制试验振动量级。

试验中，振动的正弦条件按照直升机要求的主桨频率(正弦激励)及主桨倍频正弦条件设置，随机振动范围为10Hz ～500Hz。

3.2.3 试验时间

疲劳分析中，载荷循环交变视为单位时间条件，因此每个振动条件测量进行1min采样，作用一个单位时间的载荷谱记录。

3.2.4 试验测量及载荷等代

试验测量了梁体立壁处的垂向应变时域值，如图6。

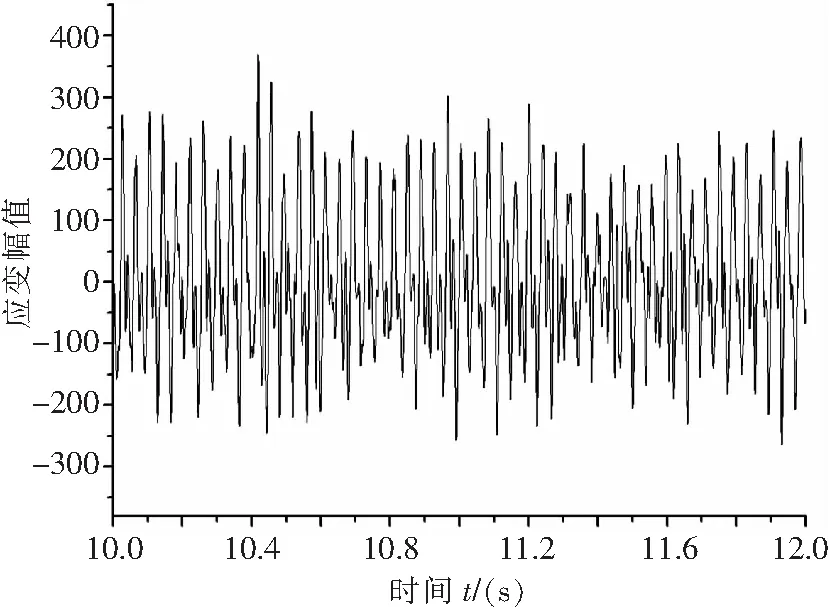
图6 梁体立壁垂向应变测量时域图(测量1min中的10s-12s)

结合静态标定试验的应变数据，计算获得梁体立壁上一个应变变化单位等于5N(每应变单位)的静态载荷。

3.2.5 有限元分析及结果

1)载荷加载

在Workbench中建立典型的梁体结构模型，选择材料为铝材。在梁体挂轨面上，加载等代垂向载荷。

2)应力集中系数

应力集中系数是在ANSYS中经对结构静力分析获得的局部最大应力值与结构应力均值的比值。参考文献[5]，结构应力集中系数

Kt

取值为1～3。经上述有限元计算，梁体危险点典型结构的应力集中系数为2.5。

3)S-N曲线

S-N应力寿命曲线是表征材料疲劳性能的重要依据，一般由试验得到。由参考文献[6]可知，在中等疲劳寿命区，应力比

R

对疲劳寿命影响显著，应力集中系数

Kt

也是导致疲劳破坏最直接的影响因素。因此，在确定了应力集中系数

Kt

和应力比

R

(-1～0.5)取值后，需修订S-N 曲线。

由于此型发射架弹体自重小，挂装载荷较小，梁体结构对应的平均应力在20MPa～70MPa之间。Workbench给出的S-N曲线疲劳极限对应值为83MPa(10e8)，不能满足本次模型的计算需求。参考文献[5]、文献[6]在材料库中补充超高周铝合金材料的应力幅-循环曲线，以满足超高周低应力幅的疲劳分析。修订、补充的S-N曲线如图7。

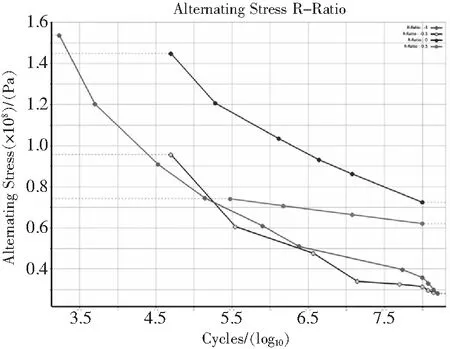
图7 应力集中系数Kt为2.5的铝合金S-N曲线图

在载荷条件中按谱域加载，采用Goodman应力疲劳理论开展计算，如图8。材料初始寿命设置为2e8，材料疲劳强度因子

kf

设置为1。计算获得的载荷谱雨流矩阵如图9，梁体结构寿命和安全系数如图10、图11。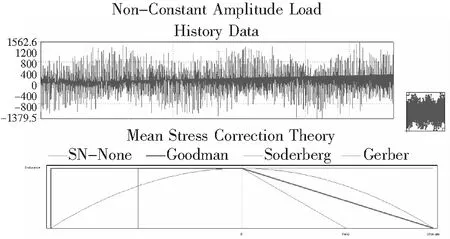

图8 1min载荷谱域与应用疲劳应力理论图

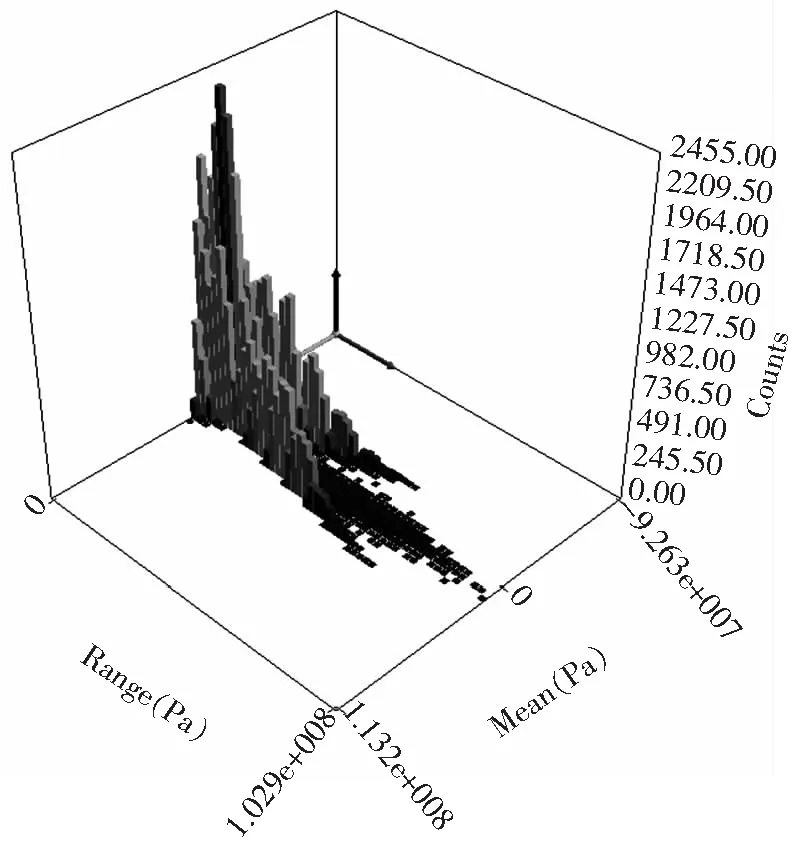
图9 梁体处完整记录1min载荷谱的雨流矩阵图。

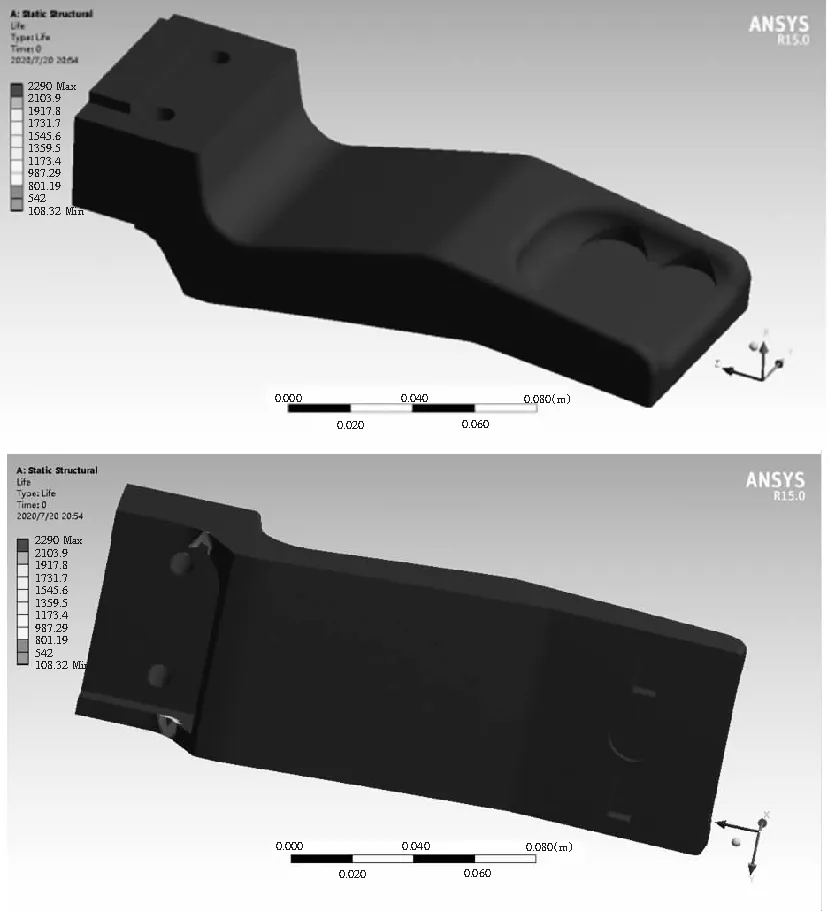
图10 梁体(对称半体)结构寿命云图

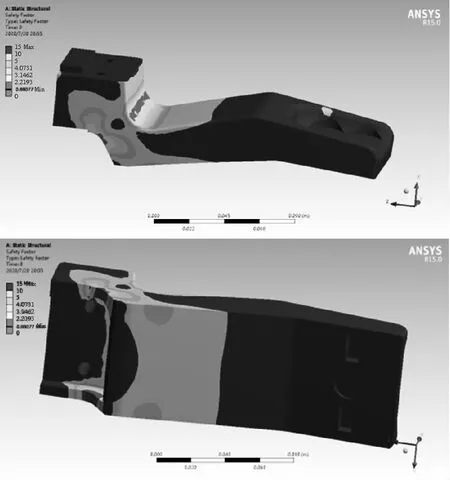
图11 梁体(对称半体)疲劳安全系数云图

经计算，1000Hz采样频率梁体疲劳寿命为104min。计算表明，在梁体下面5mm薄壁也就是应力集中点处最先出现结构疲劳。分析得出，随着疲劳损伤累积，应力集中点产生裂纹，并向上面结构体扩散，直至梁体圆弧面交界处结构疲劳出现裂纹。试验中图1照片上的实体断裂裂纹应是梁体结构疲劳断裂的最终结果。

3.3 梁体改进对比

3.3.1 结构优化

梁体原方案采用螺钉由下向上固定到发射架本体上，为了预留螺钉头及工具操作空间，梁体局部设计成5mm薄壁结构，圆弧交界处截面厚度仅12mm。结合本次问题，为提高结构强度，减少应力集中，提高抗疲劳能力，梁体采用螺钉由上向下固定，原结构梁体下面凹形槽填充平整，消除两侧5mm薄壁结构，梁体圆弧过渡处薄弱位置的截面厚度由12mm增大至26mm。结构优化前、后的梁体如图12所示。

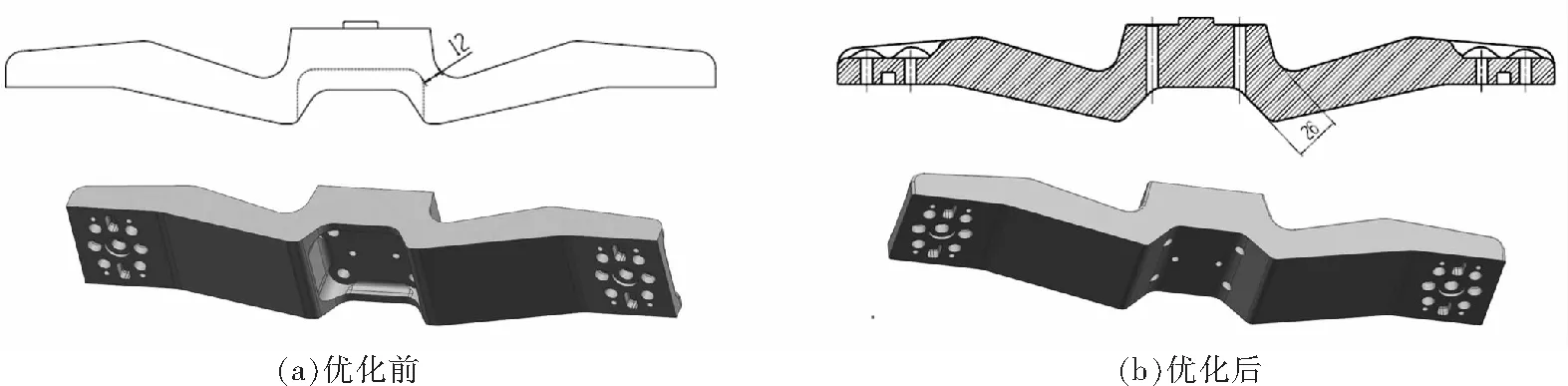
图12 优化前、后的梁体结构图

3.3.2 静强度分析

通过静载荷有限元分析，获得优化设计后的梁体结构应力值：在梁体交界面应力为40MPa，在梁体下面曲面结构的应力也为40MPa，上下结构应力均匀。优化结构与原梁体结构出现的最大应力115MPa相比，应力明显减小(图13)。同时，优化结构消除了应力集中现象。

图13 发射架优化后梁体局部静力分析

3.3.3 疲劳分析

优化后的梁体结构应力集中系数

Kt

为1，应力比

R

(-1～0.5)。

S-N 应力寿命曲线见图14。

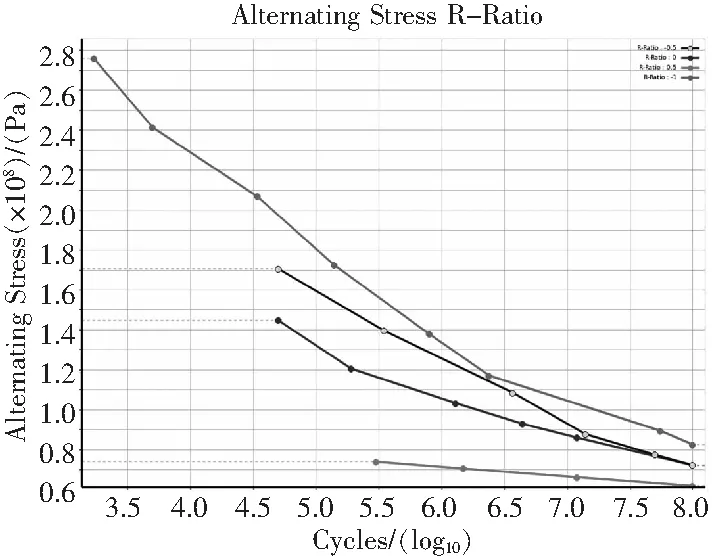
图14 应力集中系数Kt为1的铝合金S-N曲线见图

3.3.4 有限元分析及结果

梁体结构寿命和安全系数见图15、图16。

图15 优化后梁体(对称半体)结构寿命云图

图16 优化后梁体(对称半体)疲劳安全系数云图

经计算，结构优化后梁体在消除了应力集中危险点后，疲劳寿命显著增加，可以达到不少于4500min，结构疲劳区域均匀分布在梁体圆弧交界处上下面中。

3.3.5 试验验证及结果

优化后的发射架重新进行振动试验至结束，累计共进行了70h振动试验，(合计4200min)，梁体未出现断裂、裂纹现象。试验证明结构优化措施有效。

4 结论与分析

通过疲劳分析方法比较，确认应力(应变)时域分析法更适合直升机正弦+随机耦合振动条件的结构疲劳分析。基于工业部门的试验设备，应变测量、静力标定，可以在专项试验中较容易实现。

通过试验直接测量结构应变(应力)，获得的时域载荷谱及应变幅循环计数，与结构实际疲劳工况更接近，真实性较高。依据已有文献修订铝合金S-N应力寿命曲线，在有限元疲劳分析上是合理的。对比发射架振动试验结果，结构疲劳寿命与估算结果较为一致，验证了本文提出的结构疲劳估算方法的有效性和可信性。

对于在航空装备研制中经常会出现的结构疲劳问题，在装备方案设计中，试验工作开展前，关注并避免结构应力集中，合理设计结构，预计装备结构寿命，是顺利开展航空装备研制一项重要工作。