直升机旋翼桨根单摆吸振器载荷计算方法
王正峰,黄国科
(1.海装驻南昌地区军事代表室,江西 南昌 330024;2.中国直升机设计研究所,江西 景德镇 333001)
0 引言
直升机振动问题一直以来都是型号研制过程中的突出问题。与其它飞行器相比,直升机各部件是处在一个相当复杂且恶劣的振动环境下工作,旋翼、尾桨、发动机、传动装置等旋转运动部件都产生交变载荷,从而引起机体结构的振动,其中旋翼是直升机的主要振源。旋翼在周期、交变的气动环境中旋转,产生持续周期性的振动。各片桨叶上的交变振动载荷汇聚于桨毂,形成一个对于机体不旋转系统的频率为kNΩ的桨毂振动激振力与力矩。这些力与力矩就是引起机身振动的主要激振力。直升机振动会降低机体与构件的疲劳寿命,影响机上系统与设备的功能和可靠性,影响驾驶员和乘员的舒适性与任务工作效能等,因此直升机的减振技术一直是直升机研究者努力研究和解决的一个重要问题。
直升机旋翼桨根单摆吸振器是一种旋翼被动控制装置,安装在桨叶根部,利用摆球质量块的离心力起弹簧的作用。根据弹簧/质量系统动力吸振原理,摆球能够吸收旋翼桨根垂直方向激振力,减小传递给机体的旋翼桨毂激振力,从而降低直升机的振动水平。
本文建立了旋翼桨根摆式吸振器运动学模型,以单摆吸振器的摆锤为受力体进行分析。介绍了摆锤的运动学描述和坐标系定义,再根据达朗贝尔定理推导出摆球的动载荷解析表达式,最后通过编程计算,给出了桨根摆式吸振器载荷的计算案例。
1 桨根单摆吸振器建模
桨叶采用刚体假设,考虑桨叶挥舞及扭转运动,忽略桨叶摆振运动,且挥舞和扭转仅考虑主要的一阶运动。桨根单摆式吸振器采用刚体假设,摆球的摆角运动频率为单摆的固有频率。吸振器摆锤的运动学描述如图1所示。

图1 桨根单摆吸振器建模
为便于描述摆锤的运动,定义了以下几个坐标系:
1)桨毂旋转坐标系XYZ
:原点在旋转中心,由桨毂不旋转坐标系旋转方位角Ψ
得到,X
轴沿桨叶展向为正,Y
轴指向前缘为正,Z
轴指向拉力方向为正。2)桨叶挥舞坐标系X
Y
Z
:原点在挥舞铰,向上挥舞为正,X
轴沿桨叶变距轴线为正,由桨毂旋转坐标系XYZ
绕Y
轴挥舞β
得到。桨叶挥舞坐标系到桨毂旋转坐标系的转换矩阵TBR
:
(1)
3)单摆基座坐标系X
Y
Z
:原点在单摆基座转动轴中心,桨距抬头为正,X
轴沿桨叶变距轴线为正,Y
轴沿单摆转动轴轴线指向前缘为正,由桨叶挥舞坐标系X
Y
Z
绕X
轴扭转变距角θ
得到。单摆基座坐标系到桨叶挥舞坐标系的转换矩阵TθB
: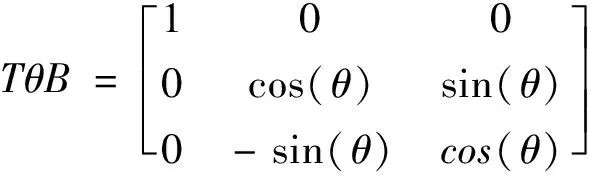
(2)
4)单摆坐标系X
Y
Z
:原点在单摆轴线与单摆基座转动轴的交点,单摆轴线在桨叶变距轴线上方为正,X
轴沿单摆轴线指向桨尖为正,由单摆基座坐标系X
Y
Z
绕Yθ
轴摆动φ
得到。单摆坐标系到单摆基座坐标系的转换矩阵TPθ
:
(3)
其中,β
为挥舞角,θ
为垂直摆基座所在剖面的桨距角,φ
为垂直摆摆角,相对于桨叶坐标系x
轴。1.1 摆球球心在各坐标系下的矢量表达
通过坐标系变化,可得到摆球球心在各坐标系中的矢量位置:
摆球球心在单摆坐标系X
Y
Z
的矢量表达:r
_Pm
=[r
0 0](4)
摆球球心在单摆基座坐标系X
Y
Z
的矢量表达:r
_θm
=r
_Pm
·TPθ
+[0l
0]=[r
cos(φ
)l
r
sin(φ
)](5)
摆球球心在桨叶挥舞坐标系X
Y
Z
的矢量表达:r
_Bm
=r
_θm
·TθB
+[L
-e
0 0]=[r
cos(φ
)+L
-e
l
cos
(θ
)-r
sin(φ
)sin(θ
)l
sin(θ
)+r
sin(φ
)cos(θ
)](6)
摆球球心在桨毂旋转坐标系XYZ
的矢量表达:r
_Rm
=r
_Bm
·TBR
+[e
0 0](7)
矩阵转置:r
_Rm
_T
=r
_Rm
,可得:
(8)
简记为:

(9)
其中,L
为垂直摆所在桨叶展向的位置,l
为基座上转动轴的一半,r
为垂直摆摆球摆长。1.2 桨毂旋转坐标系下摆球的受力
对摆球进行受力分析。根据经典力学的达朗贝尔原理,在非惯性系XYZ
中,摆球在离心力、哥氏力、惯性力、约束反力的作用下处于平衡状态,矢量表达如下: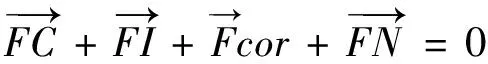
(10)
其中,FC
为摆球离心力,FI
为摆球惯性力,Fcor
为摆球哥氏力,FN
为摆球约束反力,即本文需要求解的吸振器摆臂所受的结构载荷。摆球所受的力写成矩阵形式如下:
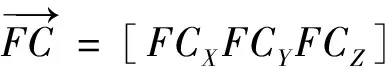
(11)
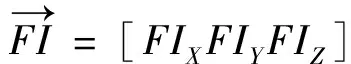
(12)

(13)
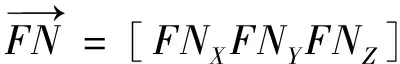
(14)
根据经典力学理论以及小角度假设,可得:
FC
=m
·Ω·r
_Rm
_T
(15)
FC
=m
·Ω·r
_Rm
_T
(16)
FC
=0(17)
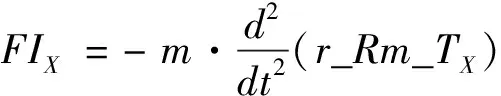
(18)
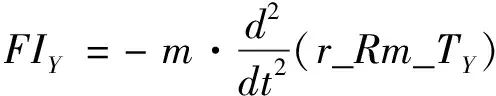
(19)

(20)
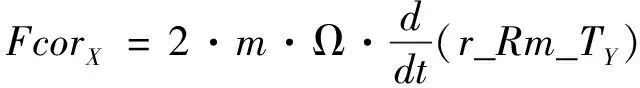
(21)

(22)
Fcor
=0(23)
各分量表达式展开简写为:
FC
=m
Ω(r
+L
-(lθ
+rφ
)β
)(24)
FC
=m
Ω(l
+rφθ
)(25)
FI
=-m
((I
1·θ
+I
2·β
+I
3)·φ
+I
4·θ
+I
5·β
+I
6)(26)
FI
=-m
(I
1·φ
+I
2·θ
+I
3)(27)
FI
=-m
((I
1·θ
+I
2·β
+I
3)·φ
+I
4·θ
+I
5·β
+I
6)(28)

(29)
Fcor
=-2m
Ω(cor
·φ
+cor
2·β
+cor
3)(30)
其中:
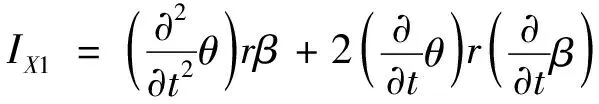
(31)

(32)

(33)
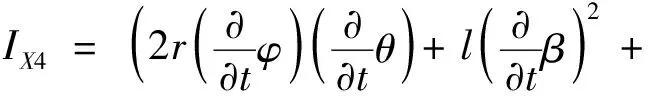

(34)

(35)


(36)
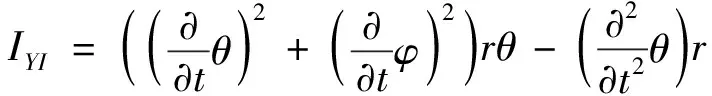
(37)
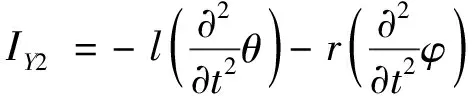
(38)

(39)
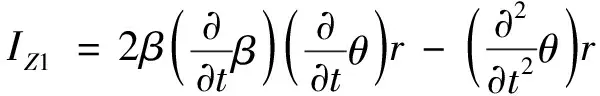
(40)

(41)

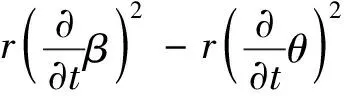
(42)
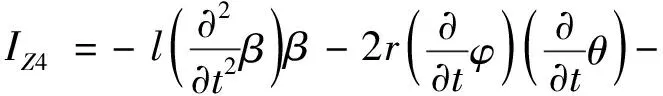
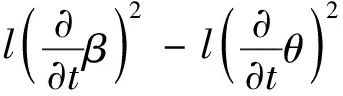
(43)
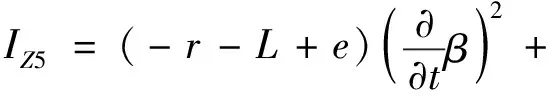

(44)
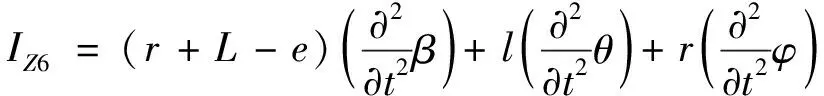
(45)
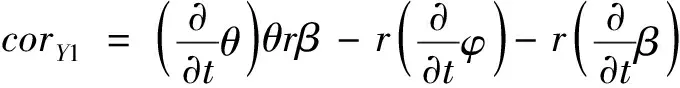
(46)

(47)
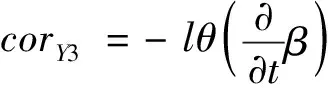
(48)
将式(10)矢量表达的力平衡方程投影到桨毂旋转坐标系XYZ
中,可得:FC
+FI
+Fcor
+FN
=0(49)
FC
+FI
+Fcor
+FN
=0(50)
FC
+FI
+Fcor
+FN
=0(51)

1.3 摆球坐标系下摆球所受的结构载荷
为便于对桨毂单摆吸振器进行强度分析,需将摆球所受的约束反力FN
从桨毂旋转坐标系XYZ
变换到单摆坐标系X
Y
Z
,从而得到摆球坐标系下桨根单摆吸振器摆球所受的结构载荷FP
。利用桨毂旋转坐标系XYZ
到单摆坐标系X
Y
Z
的转换矩阵TRP
,摆球所受的结构载荷FP
表达式可写成:FP
=FN
·TRP
(52)
其中:
TRP
=(TPθ
·TθB
·TBR
)(53)

2 算例及结果分析
根据上述推导公式,利用MATLAB进行编程,采用如表1、表2的算例参数,可得到桨根单摆吸振器摆球所受的结构载荷,见表3、图2、图3所示。

表1 旋翼总体与根单摆吸振器结构参数

表2 前进比0.2时的桨叶挥舞、变距角位移

表3 前缘/后缘摆锤在单摆坐标系下的结构载荷计算结果
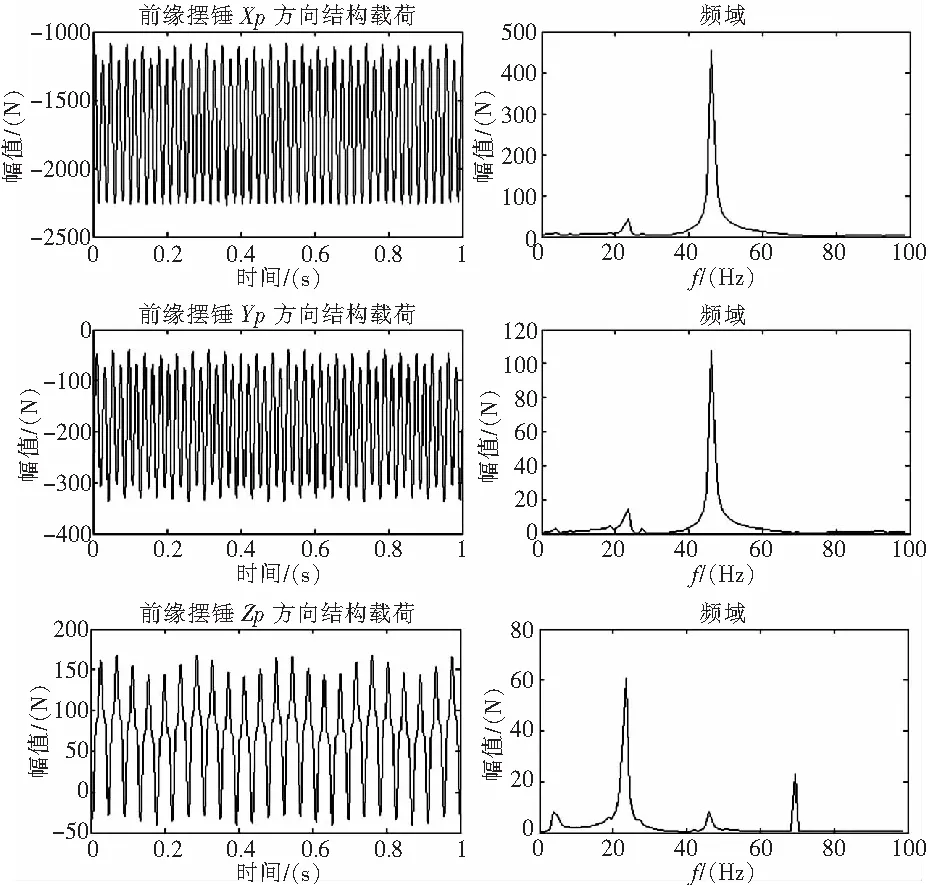
图2 前缘摆锤结构载荷
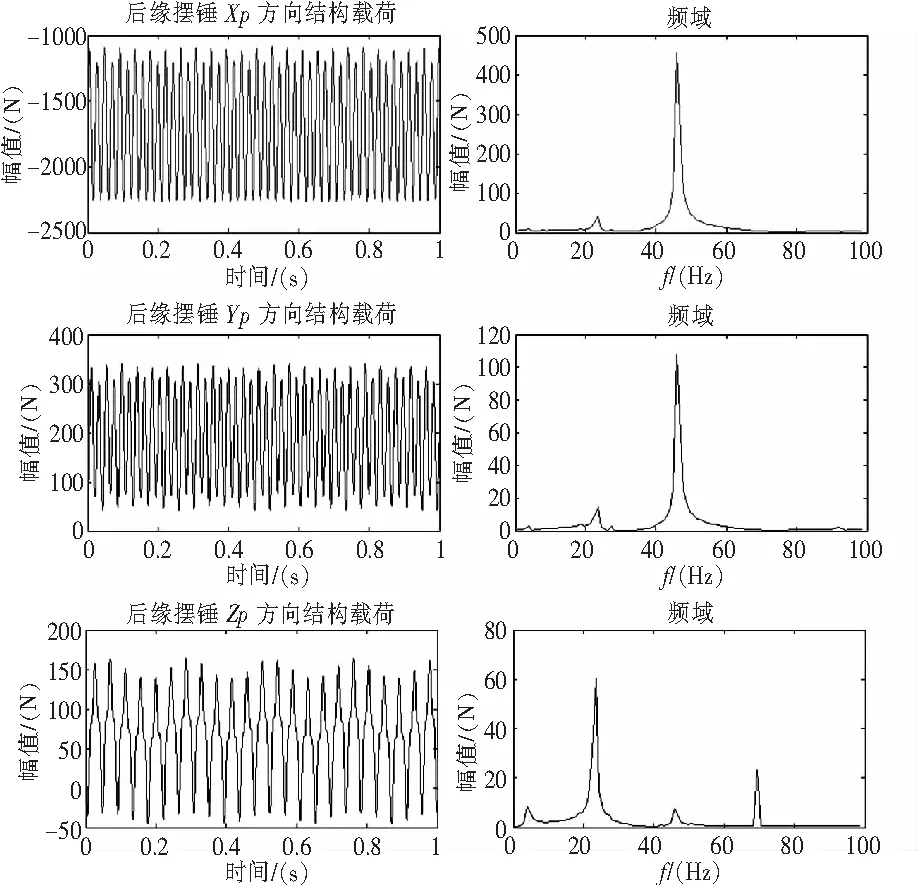
图3 后缘摆锤结构载荷
3 结论
某型机在试飞过程中曾出现挥舞方向5Ω载荷大,引起机体振动过大。在吸振器方案设计阶段,为确保吸振器工程设计的合理性,应用本论文提出的旋翼桨根单摆式吸振器载荷工程计算方法,为结构设计提供载荷输入,进行强度计算分析。加装旋翼桨根单摆式吸振器后,经试飞验证,进行加装吸振器前后的直升机振动水平对比可见,振动水平降低显著,验证了加装吸振器方案的合理性以及吸振器载荷工程计算方法的有效性。

