无人直升机吊挂运输飞行协调控制设计

蓝启城，赖水清

(1.中国船舶工业系统工程研究院，北京 100094；2.中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机吊挂飞行的动力学问题在20世纪60年代末开始受到广泛关注。最早的记载是1965年由Lucassen和Sterk所发表的文献，提出了一种垂直面内3自由度模型，采用单点吊挂假设并忽略了作用在吊挂物上的气动力和力矩。分析结果指出吊挂物摆动运动模态是稳定的，直升机长周期模态仍不稳定，并且其频率随吊索长度增加而降低。Szustak和Jenney指出，传统的直升机增稳系统在吊挂悬停和释放吊挂物过程中显得不足，可能会导致驾驶员诱发震荡现象。后来，Dukes采用了和Lucassen相同的简化方法，在频域里研究了直升机吊挂飞行的稳定性，并为吊挂飞行设计了可能行之有效的增稳措施和适宜的操纵手段，在理论上证明了在反馈机制中包含吊点的纵向移动会增强吊挂飞行的稳定性，但并未试验验证。以上研究局限于悬停和低速飞行状况，此时吊挂物的气动特性影响比较微小。Poli和Comack研究了吊挂物分别为2.44m×2.44m×6.1m的集装箱和底面直径为1.65m、长6.1m的圆柱体的前飞稳定性，研究中考虑了吊挂物的气动特性，得出长吊索、大速度和轻载荷能提高吊挂物的稳定性的结论。

随着现代传感器和控制技术的发展，尤其是差分GPS(全球定位系统)，激光雷达(光探测和测距)，全权限飞行控制系统，直升机主动飞行控制技术等的发展，直升机系统的状态感知和航迹精确控制能力显著提高，为新型直升机协调吊挂方式的实现铺平了道路。

国内相关直升机外吊挂飞行的研究集中于两所高校，且起步较晚。最早的文献发表于2004年。南京航空航天大学的研究主要集中在重型直升机外吊挂飞行的研究。北京航空航天大学主要研究重型直升机在增稳控制系统工作条件下外挂载荷运输飞行任务中的飞行品质问题。

综观国内外研究现状，国外已从直升机吊挂的基础研究发展到对改善直升机吊挂飞行品质的新方法和新型吊挂方式的研究。而国内对直升机吊挂飞行的研究主要集中在理论探索方面，将直升机、载荷和吊索视为一个多体动力学系统，导致直升机的飞行动力学建模要根据多体动力学建模要求进行简化，以降低多体动力学建模的复杂性。这些模型虽然适用于特定的分析工作，但较难根据不同的吊挂配置形式建立通用的系统动力学模型。

随着无人直升机的应用越来越广泛，大中型无人直升机的发展步伐正在不断加快，无人直升机吊挂运输将得到越来越多的应用。国外在这方面的研究较早，已经实现无人直升机吊挂运输。2011年，美国K-MAX无人直升机在世界上首次完成了吊挂运输任务。国内在这方面的研究刚刚起步，正在加大加快无人直升机吊挂运输技术的应用研究。本文针对无人直升机吊挂运输飞行，采用自抗扰控制(ADRC)方法，设计了巡航状态下吊挂飞行协调控制和目标点附近吊挂消摆轨迹规划控制策略，并进行了仿真验证。

1 直升机吊挂系统耦合动力学建模

首先建立无人直升机吊挂物的动力学模型。如图1所示，

θ

、

φ

分别表示吊挂物相对于机体的三维空间中的摆动角度，

l

为吊挂绳长。有效载荷动力学的方程非常复杂，必须执行许多数学计算。为了简化计算，我们将其条件线性化，设所有耦合和高阶项都为0。另外，可以假设以小角度状态飞行，其中sin

φ

=

φ

，cos

φ

=0，并且假设阻力为0。最终由拉格朗日法得到吊挂系统的线性化模型。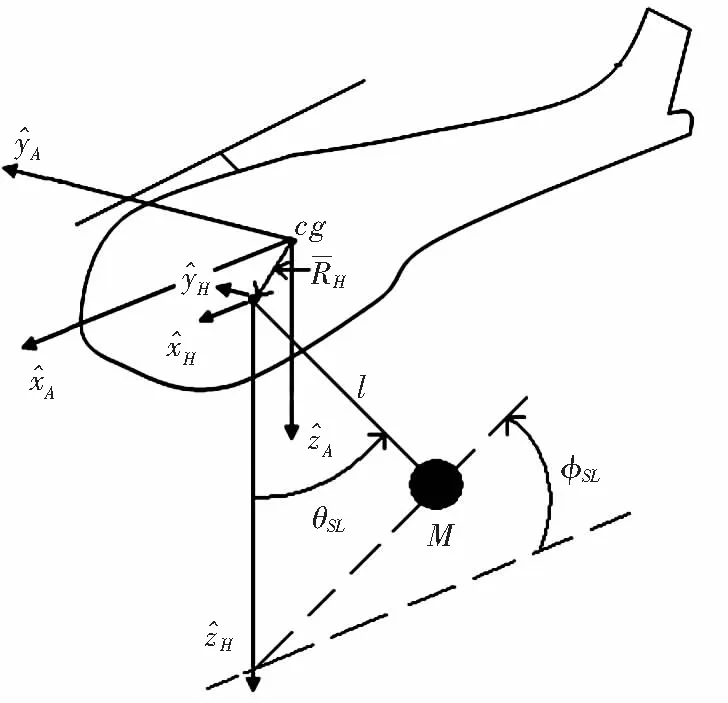

图1 无人直升机吊挂模型

由拉格朗日方程得：

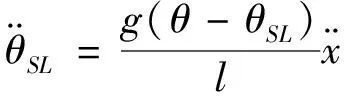
(1-1)

(1-2)

直升机吊挂耦合系统运动学可由如下方程表示：

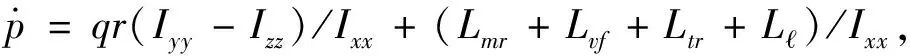
(1-3)

其中，

Z

为吊挂系统在无人直升机

Z

方向上的拉力，

M

为吊挂系统施加给无人直升机的俯仰力矩，

L

为吊挂系统施加给无人直升机的滚转力矩。

2 运输巡航状态下吊挂飞行协调控制

运输巡航飞行状态包括平飞、爬升、协调转弯等多种飞行模态。如何确保无人直升机的吊挂飞行安全，是飞行控制系统必须要解决的问题。这对吊挂无人直升机的协调控制提出了更高的要求。在这种情况下，既要保证无人直升机的稳定性，不能受吊挂物扰动的影响太大，同时又要保持吊挂物与无人直升机相对稳定，保证吊挂物不能超过最大摆动幅度。

无人直升机本身的特性决定了其是一个不确定、强耦合和易受干扰的被控对象。实现良好的飞行特性，这对设计的飞行控制系统的性能提出了很高的要求，控制器控制能力直接决定了无人机的飞行品质。传统的PID 控制很难解决无人直升机这一类被控对象的控制问题；使用先进控制方法如模糊控制、反步法控制、自适应控制，虽然可以满足直升机的飞行控制需求，但是上述方法设计困难，参数整定是个复杂的难题。ADRC 控制器对控制对象的数学模型要求却不高，其包含的扩张观测器(ESO)设计思路是利用系统输入和输出重构出系统状态，可以将内部和外部干扰，甚至系统不确定的部分都当作扰动，再去消除掉这个扰动。

2.1 ADRC控制算法的原理及特点

自抗扰控制算法是在PID控制器的基础上改良得到的一种全新控制算法。它既继承了传统PID控制的精髓(基于反馈控制，不需要被控对象的精确模型)，又融合了众多现代控制理论的思想，通过一种改进的状态观测器来获取被控对象的状态，观测模型外扰动，达到更好的控制效果。ADRC控制器结构示意见图2。

图2 ADRC控制器结构

图2中，

v

为指令输入，

v

为指令输入过渡过程，

v

为指令输入过渡过程的微分，

ω

(

t

)为外界干扰，

z

为实际输入，

z

为实际输入的微分，

z

为误外界扰动补偿量，

u

为实际控制量输出。

自抗扰控制器由跟踪微分器、状态扩张器和非线性反馈控制律三个部分组成。它的核心部分是扩张状态观测器。其中，跟踪微分器的作用是安排过渡过程，扩张状态观测器则用来估计系统状态、模型和外扰。非线性反馈控制率是把未知外扰的非线性不确定对象用非线性状态反馈化为“积分串联型”，是一种对非线性不确定对象实现反馈线性化的结构,而且是一种动态反馈线性化。

从ADRC的提出至今，许多实物试验和仿真试验都证明了ADRC能够获得良好的动态性能且具有良好的性能鲁棒性。自抗扰控制器的独特思想和结构决定了该方法具有如下优点：

一是结构简单。该方法具有与传统PID非常相近的简单结构，易于被工程人员掌握。例如线性形式的3阶ADRC(指ADRC中的ESO阶数为3)，可以看成是一个比例微分(PD)控制器加上扩张状态(

z

)的观测和补偿，当信号

z

被去掉时控制器则完全转为PD控制器。

二是反应敏捷。传统PID控制都要等到误差发生后才能去补偿控制；而ADRC则将观察到的扰动第一时间补偿到输出端。而且，PID中的微分项D，虽然说有预测功能，但它仅仅是将本次的误差减去上一次的误差，得到很粗劣的微分结果；而ADRC使用跟踪微分器，准确跟踪目标值的微分(图中的跟踪加速度)，用扩张状态观测器得出实际值的微分(图中的观测加速度)，两个相减即为准确的误差微分。

三是不依赖于对象模型，具有很强的适应性。ADRC适用于从对对象模型一无所知到完全掌握对象模型的任何情况。当然，如果能准确捕捉到这个关系，ADRC工作强度将减轻，效果更佳。

四是很强的抗干扰能力。将系统的非线性、模型不确定性和外部扰动等都视为系统的扩张状态加以观测，然后利用控制率进行补偿。

五是解耦特性。对于MIMO系统，自抗扰PID控制方法将系统变量间的各种耦合作用统一看成系统的扩张状态加以考虑，从而避免了需要单独设计静态或动态解耦模块后才能设计控制器的窘境，同时又不降低控制系统的性能。

六是易用性。ADRC在最初推出时虽然性能惊人，但是要调试的参数非常多，不容易使用。随着Scaling and Bandwidth-Parameterization等理论的提出，ADRC参数调整变得简单多了。

七是灵活性。ADRC是在PID的启发下发展出来的，一般只要有PID的地方，都可以直接用ADRC替换。

2.2 控制器设计

飞行控制器采用双闭环控制策略，内环为姿态控制，外环为位置控制(见图3)。位置ADRC输入量为实际位置(

x

，

y

，

z

)与期望位置(

x

，

y

，

z

)，输出量是期望姿态角(

φ

，

θ

)和控制量

U

。姿态ADRC根据期望姿态与实际姿态关系得到三个方向的控制量(

U

，

U

，

U

)。

图3 控制器整体结构框图

2.2.1 内环ADRC控制器设计

对无人直升机内环通道分别应用ADRC控制策略(见图4)，控制器根据期望姿态与实际姿态关系得到三个方向的控制量(

U

，

U

，

U

)。

图4 内环ADRC控制器结构框图

以内环滚转角回路控制器为例，借助于ESO估计出的回路扰动量，对系统进行动态补偿，可以使得滚转角回路近似为积分串联型系统。滚转角回路ADRC算法如下：

1)安排过渡过程

(2-1)

式中，

r

为快速因子，

h

为滤波因子。

r

越大，跟踪的速度越快，但噪声放大也越大；

h

越大，滤波效果越好，但跟踪的效果变差。

2)估计状态和总扰动(ESO方程)

(2-2)

式中，

β

、

β

、

β

为状态误差反馈的反馈增益，影响ESO的收敛速度；

h

为控制周期，考虑到实际应用，

h

取为0.01；

δ

为

fal

函数的线性区间宽度，用来消除高频脉动的产生。

3)控制量的形成

(2-3)

式中，

M

为控制器计算输出的滚转力矩。

2.2.2 位置环ADRC控制器设计

位置环ADRC控制器对直升机三个方向的位置分别进行ADRC控制。位置ADRC输入量为实际位置(

x

，

y

，

z

)与期望位置(

x

，

y

，

z

)，得到三个方向的虚拟控制量。继而通过虚拟控制量与实际控制输出之间的转换得到期望姿态角(

φ

，

θ

)和控制量

U

。期望姿态角进入姿态环进行姿态环控制。位置环ADRC控制器结构框图见图5。

图5 位置环ADRC控制器结构框图

(2-4)

式中，

w

为该通道总扰动，

u

为虚拟控制量，

b

为控制通道增益，此处为1。与姿态控制器类似，应用TD安排过渡过程。TD 的输入

v

代表此处的

x

，输出(

v

,

v

)。

对于状态误差反馈率，考虑到位置控制器输出的控制量主要为姿态角，为了便于姿态控制器跟踪，选用式(2-4)描述的控制律，使控制输出更为平滑。式中(

k

，

k

)与PD控制器参数的意义相同。

(2-5)

Y

方向与

Z

方向的控制器设计与

X

方向的方法一致。

3 目标点附近吊挂消摆轨迹规划控制

无人直升机吊挂运输旨在将其吊挂的负载平稳、安全、高效地运送至指定位置。欠驱动系统由于独立控制量数目少于系统自由度，从而给其控制带来了很大的困难。而无人直升机吊挂运输系统具有典型的欠驱动特性，负载不能直接通过驱动器控制，而只能通过对无人直升机的运动进行设计来间接控制负载的运动。我们需要无人直升机在通过航迹规划到达目标点时进行卸载、着陆作业，但此时吊挂物很可能在不断地摆动，这会影响无人直升机的稳定性，出现危险。为了防止此类现象出现，确保作业安全性，希望无人直升机在到达目的地后，吊挂负载无残余摆动。充分考虑无人直升机吊挂运输的速度、加速度等物理约束，以及无人直升机与吊挂物之间的非线性耦合关系，采用S曲线生成法进行动态规划控制，消除吊挂物的残余摆动。

3.1 S曲线算法原理

典型S型曲线的速度、加速度以及加加速度随时间变化曲线如图6所示。其中，

v

为系统最大速度，

a

为系统最大加速度，

j

为系统加加速度，

t

为加加速时间，

t

为加速时间，

t

为总运动时间。

图6 典型S曲线图

对任意时刻，S型曲线的位移、速度、加速度可表示为：

(3-1)

a

(

t

)=

(3-2)

3.2 轨迹策略生成

该轨迹如图7所示。其中参数分别表示加速区间，匀速区间，减速区间以及最高速度。

图7 S型曲线速度轨迹

S型曲线速度轨道为：

(3-3)

式中，

A

=

v/

2,

ω

=

π/t

,

ω

=

π/t

,

t

=

t

-

t

-

t

,

T

=

t

+

t

。

取式(3-3)的时间导数，得到其加速度轨迹：

(3-4)

为了验证算法，出于可靠性，我们只考虑二维平面摆动情况，即只对

θ

进行消摆处理。

(3-5)

(3-6)

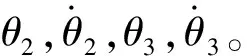
θ

(

T

)=0

(3-7)

4 仿真验证

4.1 运输巡航状态下吊挂飞行协调控制仿真

在Matlab仿真环境下，对运输巡航状态下吊挂飞行协调控制算法进行仿真验证，结果如图8、图9。

图8 运动状态下的横向跟踪情况

图9 运动状态下的纵向跟踪情况

图8中绿线表示动态时使用ADRC的横滚角速率设定值，黑线表示动态时使用ADRC的横滚角速率测量值。

图9中绿线表示动态时使用ADRC的俯仰角速率设定值，黑线表示动态时使用ADRC的俯仰角速率测量值。

仿真结果表明，动态响应的响应时间基本都在60～80ms之间，超调量很小。在恢复到稳态时，ADRC控制的无人直升机飞行平稳，跟踪性能良好，静态误差很小。

4.2 目标点附近吊挂消摆轨迹规划控制仿真

在Matlab仿真环境下，对目标点附近吊挂消摆轨迹规划控制算法进行仿真验证，结果如图10-图12。

图10 吊挂负载摆动角度

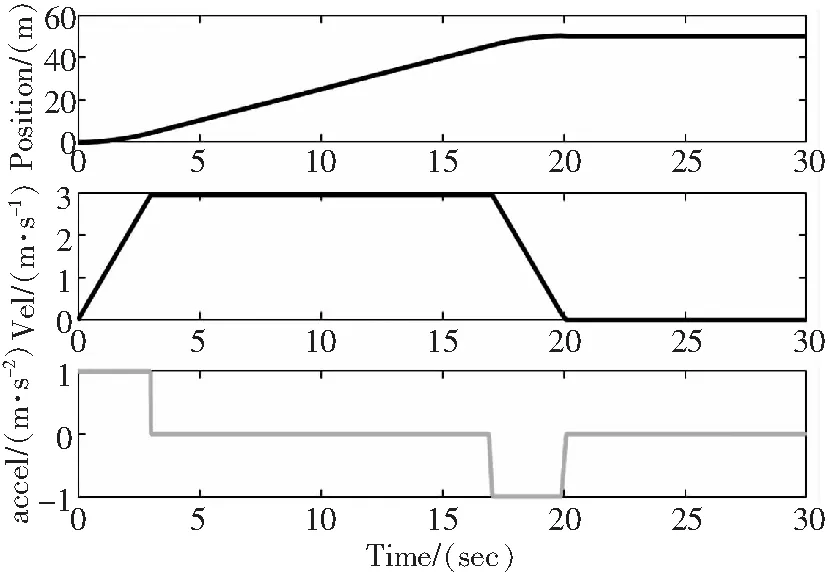
图11 无人机平移规划运动轨迹

图12 吊挂负载摆动角度

1)无轨迹规划下的吊挂物摆动情况

仿真结果表明，在没有轨迹规划的情况，在20s时，当无人直升机达到预设位置停止后，吊挂负载持续摆动。

2)S曲线轨迹规划下的吊挂物摆动情况

仿真结果表明，在进行S曲线轨迹规划下，在20s时，当无人直升机达到预设位置停止后，吊挂负载停止摆动，且摆角基本保持在0°，消摆效果明显。

5 结论

本文采用自抗扰控制技术，引入虚拟控制量对位置和姿态进行控制解耦，应用扩张状态观测器进行状态解耦和扰动估计，较好地实现了无人直升机吊挂耦合系统的解耦，能够较好地解决状态耦合、外部扰动和被控对象参数摄动等问题。仿真验证说明，无论是在动态特性还是稳态特性上，自抗扰控制都具有较好的抗干扰能力与稳定性。因此，自抗扰控制器应用于无人直升机吊挂运输飞行协调控制是可行的，对于扰动的控制也是有效的。