重型车荷载对公路斜拉桥振动响应的影响
陈水生, 赵辉, 李锦华, 王屹昊, 夏钰桓
(1. 华东交通大学土木建筑学院, 江西 南昌 330013; 2. 湖北恒大建设工程有限公司, 湖北 武穴 435400)
0 引言
随着我国经济的快速发展, 逐年增加的交通量给在役公路桥梁带来巨大的压力和挑战, 特别是车辆超重而导致的桥梁垮塌事故时有发生, 桥梁结构在重型车荷载作用下的使用寿命和运营安全备受社会关注. 因此, 学者们对桥梁在重型车荷载作用下的荷载效应研究做了很多工作, 基于WIM系统对城市桥梁和高速公路桥梁的汽车荷载进行调查并建立城市桥梁和高速公路桥梁的重型车疲劳荷载模型[1-2], 进而研究不同结构类型桥梁在重型车荷载作用下的荷载效应[3-7]. 也有学者对大跨度公路斜拉桥的车桥耦合振动进行研究, 如Song等[8]将车辆简化为1/4车或1/2车分析斜拉桥的振动响应, 结果表明采用模态叠加法求解桥梁的振动响应时, 桥面主梁的振动响应比斜拉索需要更多的模态; Zhang等[9]研究表明, 斜拉索的局部振动不明显, 移动车辆荷载对拉索张力的影响大于对主梁和桥塔位移的影响; 谢旭等[10]研究发现, 斜拉桥的动力系数离散性很大, 与所选取的响应点位置有关, 如果用单一的挠度动力系数来研究车辆荷载对斜拉桥的冲击作用非常不合理; 刘全民等[11]将车辆简化为9自由度3轴整车模型, 结果表明独塔斜拉桥钢-混结合段的振动响应随车辆荷载的增大而显著增大, 超载车辆过桥对结合段危害较大; 万信华等[12]研究了斜拉桥在2轴1/2车车列荷载作用下的振动响应. 但是, 上述有关大跨度公路斜拉桥车桥耦合振动研究的车辆载重量和车辆尺寸较小, 且车辆模型过于简化. 因此, 本文建立一辆六轴重型车的三维振动模型, 分析重型车荷载激励的斜拉桥纵梁、 桥塔和斜拉索的振动响应, 为类似斜拉桥的建造和管养提供参考依据.
1 车桥耦合振动理论
1.1 重型车振动模型
有研究表明, 重型车中六轴车的出现频率较高[13], 且我国《公路桥涵设计通用规范(JTG D60—2015)》规定的公路-Ⅰ级疲劳车辆荷载计算模型Ⅱ也为六轴车[14]. 因此, 本文采用传统弹簧-质量-阻尼振动体系将一辆六轴拖挂车简化为17自由度空间模型, 同时考虑牵引车和挂车的竖向振动、 纵向点头和侧翻, 车辆模型如图1所示, 车辆悬挂系统参数和几何参数参考文献[13, 15].

图1 车辆模型Fig.1 Vehicle model
根据虚功原理, 建立17自由度车辆振动方程:

(1)

1.2 桥梁振动模型
以鄱阳湖二桥为分析对象, 该桥为五跨双塔空间双索面钢-混凝土组合梁斜拉桥, 连接江西省都昌县和庐山市, 主跨420 m, 桥面以上塔高107.6 m, 72对斜拉索呈双索面扇形布置, 拉索最大长度为223.042 m(编号: WZ18、 EZ18), 拉索最小长度为60.168 m(编号: WZ1、 EZ1). 主梁钢构架由纵梁、 横梁、 小纵梁和压重小纵梁通过节点板及高强螺栓连接而成, 两个纵梁间距26 m, 纵向钢梁之间设置3道小纵梁, 间距分别为6、 7、 7、 6 m. 桥梁设计荷载为公路-Ⅰ级, 设计车速为100 km·h-1, 双向四车道, 桥梁横断面图如图2所示.
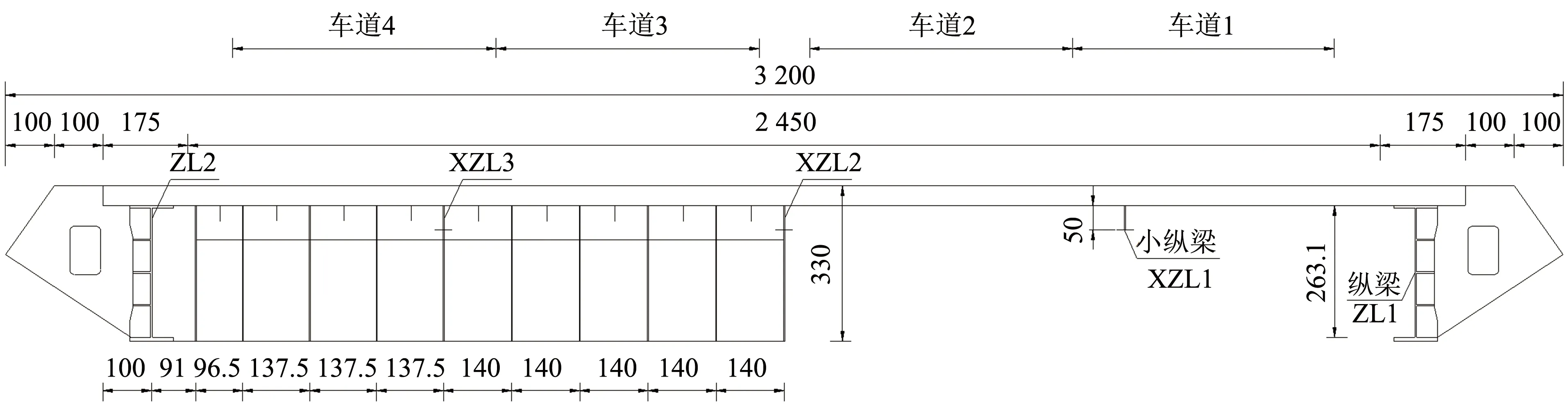
图2 桥梁横断面图(单位: cm)Fig.2 Cross section of bridge(unit: cm)
为减少车桥耦合计算矩阵维数, 根据模态综合法, 桥梁的振动方程可以表示为:

(2)
式中:fg为车辆总质量引起的各车轮作用点处的荷载向量;ξn为桥梁第n阶阻尼比;ωn为桥梁第n阶自振频率;Φ为桥梁n阶振型向量矩阵;y为桥梁广义坐标列向量.
1.3 车桥耦合模型
通过车轮与桥面接触处的位移协调条件和相互作用力平衡条件, 可得第i个车轮作用在桥梁上的荷载:

(3)
式中:Ni为第i车轮作用处位移场的插值函数;Ni, x为Ni对车辆行驶方向x坐标的导数;fgi为第i车轮所承受的车辆总质量.
将式(3)代入式(2)可得:

(4)
联立式(4)和式(1), 可得车桥耦合振动方程:

(5)


(6)

(7)
2 桥梁动力特性分析
采用ANSYS软件建立鄱阳湖二桥的杆系有限元模型如图3所示, 其中钢主梁、 钢横梁和桥塔采用Beam4梁单元模拟, 斜拉索采用Link10杆单元模拟, 桥面板和铺装层采用Shell63壳单元模拟. 沿桥梁纵向不设约束, 桥塔与纵梁之间通过横桥向自由度耦合来模拟其边界条件, 过渡墩与主梁的连接部位约束竖向、 横向位移自由度和绕桥梁纵向的转动自由度, 辅助墩与主梁的连接部位约束竖向位移自由度和绕桥梁纵向的转动自由度, 塔墩与基础按照固结处理. 考虑斜拉索几何非线性的影响, 在进行斜拉桥的动力特性分析前, 按照设计要求输入斜拉索的初始应变来模拟初拉力对结构动力特性产生的影响.

图3 桥梁有限元模型Fig.3 Finite element model of bridge
ANSYS提取的桥梁前十阶频率和振型如表1所示. 从表1可看出, 鄱阳湖二桥表现出的振型特点主要以纵漂、 竖向弯曲、 侧向弯曲和扭转为主. 由于桥梁各方向的刚度不同, 相应振型出现的次序也不相同, 主梁竖向弯曲振型表现明显且最早出现在第2阶, 主梁侧向弯曲出现在第3阶, 说明桥梁竖向抗弯刚度较低, 且横向刚度大于竖向刚度; 第5阶和第6阶出现桥塔侧向弯曲, 说明桥塔横向刚度较弱; 主梁扭转振型只出现在第9阶, 说明桥梁抗扭刚度较大.

表1 桥梁前10阶频率及振型特征
3 桥梁振动响应分析
为研究方便, 分三种工况探讨重型车对斜拉桥振动响应的影响: 工况一, 车速60 km·h-1, 车身质量随机; 工况二, 车身质量90 t, 车速随机; 工况三, 车身质量和车速都随机. 在无特殊说明的情况下, 下文桥面路况等级为B级, 车辆在行车道行驶, 行驶方向由庐山驶向都昌. 因为鄱阳湖二桥为对称结构, 只取庐山到都昌方向的边跨、 次边跨和主跨为分析对象.
实际上, 每一辆过桥重型车车身质量和车速是各不相同的, 有很大的随机性, 已有研究表明高速公路上重型车的车身质量服从双峰型概率分布, 车辆行驶速度服从正态分布[16]. 根据某高速公路的实测WIM监测数据, 重型车车身质量和车速的统计数据如表2所示.

表2 车身质量和车速统计数据
3.1 纵梁振动响应
不考虑车身质量和车速的随机性, 当一辆质量为90 t的重型车以60 km·h-1速度在车道1行驶时, 边跨、 次边跨和主跨的纵梁ZL1跨中振动响应如图4所示. 从图4可看出: 1)各跨纵梁的跨中纵向位移接近; 2)边跨纵梁的跨中竖向位移最小, 次边跨次之, 而主跨最大, 各跨跨中竖向位移最大值分别为3.6、 5.9、 82.71 mm; 3)边跨和次边跨纵梁跨中横向振动响应相同, 但主跨纵梁跨中横向振动响应较大, 各跨跨中横向位移最大值分别为0.24、 0.24、 0.71 mm. 可见, 斜拉桥纵梁的横向位移最小, 纵向位移次之, 竖向位移最大, 这与上文分析的斜拉桥各部位的刚度强弱是一致的. 按照我国《公路斜拉桥设计规范(JTG/T 3365-01—2020)》的规定[17], 汽车荷载引起的纵梁正负挠度绝对值之和应小于l/400,l为计算跨径, 鄱阳湖二桥主跨纵梁在90 t车辆荷载作用下的正负挠度绝对值之和为89.98 mm, 小于规范值1 050 mm, 主梁刚度是满足规范要求的.

图4 纵梁ZL1振动响应Fig.4 Vibration response of longitudinal beam ZL1
采用蒙特卡罗随机抽样的方法, 生成10 000辆车身质量和车速随机的重型车, 计算每一辆重型车过桥引起的桥梁振动响应, 并对每一辆重型车过桥产生的桥梁振动响应最大值进行统计分析. 三种不同的工况, 纵梁ZL1跨中最大竖向位移的概率密度曲线如图5所示, 从图5可看出: 1)工况一和工况三的最大位移响应概率密度曲线都呈现双峰分布的特征, 且最大位移响应值主要分布在两个概率密度峰值27和60 mm附近, 超过90 mm的概率只有1.7%, 最大位移响应的均值为47.27 mm, 标准差为17.45 mm, 最大响应值的离散程度较大, 空车过桥的振动响应最大值为15.94 mm; 2)工况二的最大位移响应概率密度曲线分布呈现单峰分布的特征, 最大位移响应值主要分布在峰值56.59 mm附近, 超过60 mm的概率只有0.9%, 最大位移响应的均值为57.06 mm, 标准差为0.74 mm, 最大响应值的离散程度较小. 可见, 纵梁跨中振动响应的幅值受车身质量的影响较大, 而车速对纵梁振动响应的影响不如车身质量明显; 限制重型车的载重量可以有效避免纵梁产生过大的振动响应, 也可以减小桥梁振动响应的离散程度.

图5 纵梁跨中最大竖向位移响应的概率密度Fig.5 Probability density of maximum vertical displacement response of longitudinal beam in mid-span
3.2 桥塔振动响应

图6 塔顶振动响应Fig.6 Vibration response of tower top
以西侧桥塔为例, 不考虑车身质量和车速的随机性, 当一辆质量为90 t的重型车以60 km·h-1速度在车道1行驶时, 桥塔塔顶的振动响应如图6所示. 从图6可看出, 桥塔纵向振动响应最大, 横向振动响应次之, 竖向振动响应最小, 其最大值分别为19.22、 4.58、 0.81 mm, 桥塔的纵向位移响应应该引起重视, 而竖向位移响应可以忽略不计.
考虑重型车车身质量和车速的随机性, 不同工况的塔顶最大纵向位移响应的概率密度曲线如图7所示. 从图7可看出: 1)工况一和工况三的最大位移响应概率密度曲线分布都呈现双峰分布的特征, 最大位移响应值主要分布在两个概率密度峰值8.72和18.64 mm附近, 超过30 mm的概率为1.2%, 最大位移响应的均值为15.29 mm, 标准差为5.46 mm, 最大响应值的离散程度较大, 空车过桥引起的塔顶纵向位移响应最大值为5 mm; 2)工况二的最大位移响应概率密度曲线分布呈现单峰分布的特征, 最大位移响应值主要分布在峰值18.04 mm附近, 超过20 mm的概率为0.9%, 最大位移响应的均值为17.74 mm, 标准差为1.03 mm, 最大响应值的离散程度较小, 最大位移响应主要分布在16.6~19.1 mm的区间.

图7 塔顶最大纵向位移响应的概率密度Fig.7 Probability density of maximum longitudinal displacement response of tower top
3.3 拉索振动响应
不考虑车身质量和车速的随机性, 当一辆质量为90 t的重型车以60 km·h-1速度在车道1行驶时, 以西塔南侧的36根斜拉索为分析对象, 主跨最长拉索WZ18中点的振动响应和西塔南侧其他各拉索中点的振动响应最大值如图8所示.


图8 拉索中点的振动响应Fig.8 Vibration response of cable midpoint
从图8可看出: 1) 拉索的面内振动响应最大, 轴向振动响应次之, 而面外振动响应最小, 三者的最大响应值分别为31.65、 26.72、 1.67 mm; 2) 较长拉索的轴向振动响应大于较短拉索的轴向振动响应, 各拉索的轴向振动响应随着拉索长度的增加而增大; 3) 桥梁边跨拉索的面外振动响应随着拉索长度的增加而增大, 次边跨拉索的面外振动响应随着拉索长度的增加而减小, 主跨拉索WZ1~WZ10面外振动响应随着拉索长度的增加而减小, 而拉索WZ10~WZ18面外振动响应随着拉索长度的增加而增大; 拉索WB9的面外振动响应最小, 拉索WZ18面外振动响应最大; 4) 在重型车荷载激励下, 主跨拉索WZ1~WZ10面内振动响应最大值相差较小, 但拉索WZ10~WZ18的面内振动响应最大值随着拉索长度的增加而增大.
考虑车身质量和车速的随机性, 不同工况的拉索WZ18中点轴向和面内最大振动响应的概率密度如图9~10所示.

图9 轴向振动 Fig.9 Axial vibration
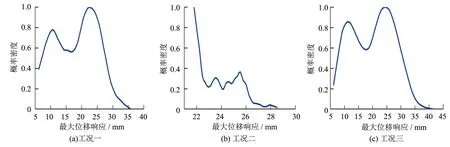
图10 面内振动 Fig.10 In plane vibration
从图9~10可看出: 1) 工况一和工况三的拉索振动响应最大值的概率密度分布呈现双峰分布的特点, 说明拉索振动响应的大小受车辆载重量的影响较大; 最大轴向振动响应主要分布在8.37和19.1 mm附近, 最大面内振动响应主要分布在10.93和24.67 mm附近; 2) 工况二的拉索轴向和面内振动响应最大值的概率密度分布呈现出多峰分布的特征, 离散性较大; 3) 拉索WZ18的轴向、 面内振动响应最大值分别超过32、 40 mm的概率为1.7%、 0.4%.
4 结语
1) 车身质量对斜拉桥纵梁、 桥塔和斜拉索的影响大于车速的影响, 桥梁各构件振动响应最大值的概率密度分布与车身质量的概率密度分布相同, 具有双峰分布的特征.
2) 各拉索轴向振动响应随着拉索长度的增加而增大, 面外振动响应因拉索长度不同而各异, 主跨WZ10~WZ18拉索的面内振动响应随着拉索长度的增加而增大, 其他拉索的面内振动响应幅值相差较小.
3) 在斜拉桥的建造和管养中, 纵梁竖向振动、 塔顶纵向振动、 长拉索的轴向和面内振动是控制重点, 应重点关注.

