基于CNN-SVM的调制方式识别优化算法

念茂， 郭里婷, 陈平平

(福州大学物理与信息工程学院， 福建 福州 350108)

0 引言

调制识别是指在不了解接收信号的情况下, 确定其调制类型的一种技术手段[1]， 被广泛运用在军事和民用领域. 传统的调制识别算法可以分为两大类[2]： 基于决策理论的方法和基于统计模式识别的方法. 决策论方法是基于概率论和假设检验原理[3], 计算量大且复杂; 而基于统计模式的方法主要在于对特征的选择和提取， 根据所提取到的特征选用特定的分类器对其进行分类识别. 相比之下， 基于统计模式的方法更加简单易实现， 因此其得到更广泛的应用.

近年来， 深度学习在图像识别领域得到了广泛的应用[4]. 能够通过对图像的学习来自动地提取其特征， 渐渐取代了人工提取特征， 因此在分类识别算法方面受到了众多科研工作者的青睐. 文献[5]提出一种利用深度稀疏卷积神经网络来提取信号循环谱特征的方法. 该方法所需要的训练样本过大， 进而导致训练时间长， 并且在0 dB信噪比时识别率仅为90%， 因此该方法实用性较差. 文献[6]提出基于高阶累积量的识别方法， 并根据高阶累积量设计特征参量， 以此作为判断阈值来对不同的已调信号进行分类识别， 该算法由于人为设计特征值， 加大算法的计算复杂度， 并且在信噪比为10 dB时才能达到96%的正确识别率， 低信噪比下的分类结果不尽如人意. 文献[7]提出提取信号循环谱的等高图获得二维特征信息， 并采用卷积神经网络对二维特征信息进行训练分类的算法， 但该算法在信噪比为0 dB时仅有90.17%的准确识别率， 识别效果较为一般.

本研究对不同已调信号采用谱平滑周期图法做循环谱估计， 生成循环谱图， 截取循环谱等高图作为特征图， 然后利用卷积神经网络(convolution neural network, CNN)和t分布邻域嵌入算法(t-distributed stochastic neighbor embedding,t-SNE)结合形成的特征提取器来提取特征， 由于支持向量机(support vector machine, SVM)在小样本的情况下具有极佳的分类性能， 并且其擅长处理非线性的分类问题以及具有较好的结构稳定性， 因此将提取到的特征值输入到SVM来进行分类， 实现已调信号的有效分类识别. 实验仿真结果表明， 该算法不仅表现出了较好的识别效果， 在SNR较低的环境依然保持较高的识别准确率， 并且具有较强的鲁棒性.

1 循环谱估计与图像预处理

1.1 循环理论分析

平稳噪声信号的统计均值为常量， 其循环均值和循环自相关函数在非零循环频率上恒为0， 即平稳噪声不具有循环平稳性[8]， 因此信号的循环谱具有很好的抗噪性能， 对后续提升模型的准确分类提供了有力的支撑.

通信系统传输模型表达式如下:

r(t)=x(t)+n(t)

(1)

其中:r(t)表示接收到的信号；x(t)代表经过调制后的信号；n(t)为信道产生的随机噪声.Rx(t;τ)为信号r(t)的广义循环平稳过程自相关函数， 表示如下：

Rx(t;τ)=E{r(t)r*(t-τ)}

(2)

这里,τ表示时间间隔.将Rx(t;τ)用傅里叶展开：

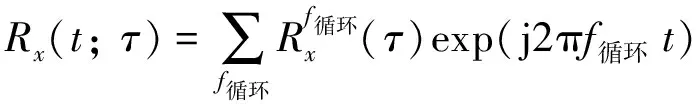
(3)

(4)

(5)

1.2 循环谱图处理

常用的循环谱估计算法有基于时域的快速傅里叶累加算法(FAM)、 SSCA算法、 时域平滑周期图法， 以及基于频域的数字频域平滑算法(DFSM)和谱平滑周期图法. 本研究采用计算速度较快的谱平滑周期图算法来对调制信号做循环谱估计. 计算过程如下：

对信号x(t)做傅里叶变换：

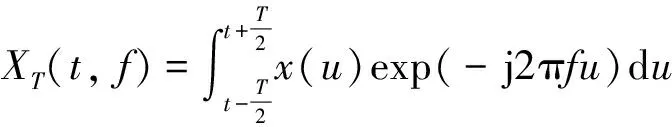
(6)

并且循环谱周期图为：

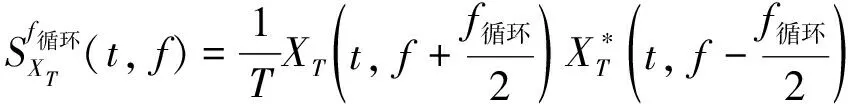
(7)

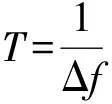
(8)

这里，

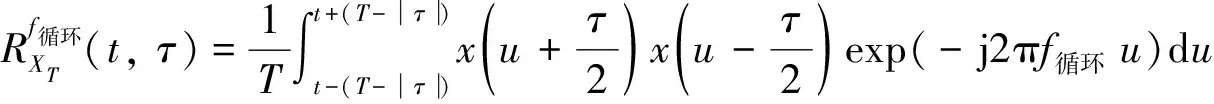
(9)

式(9)为周期相关图. 则谱平滑周期图的循环谱估计函数为：

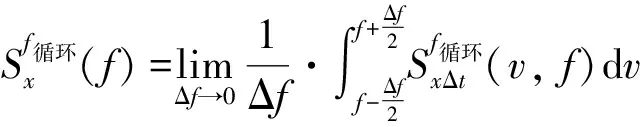
(10)

对六种已调信号利用上述谱平滑周期图法计算生成循环谱图， 如图1所示：

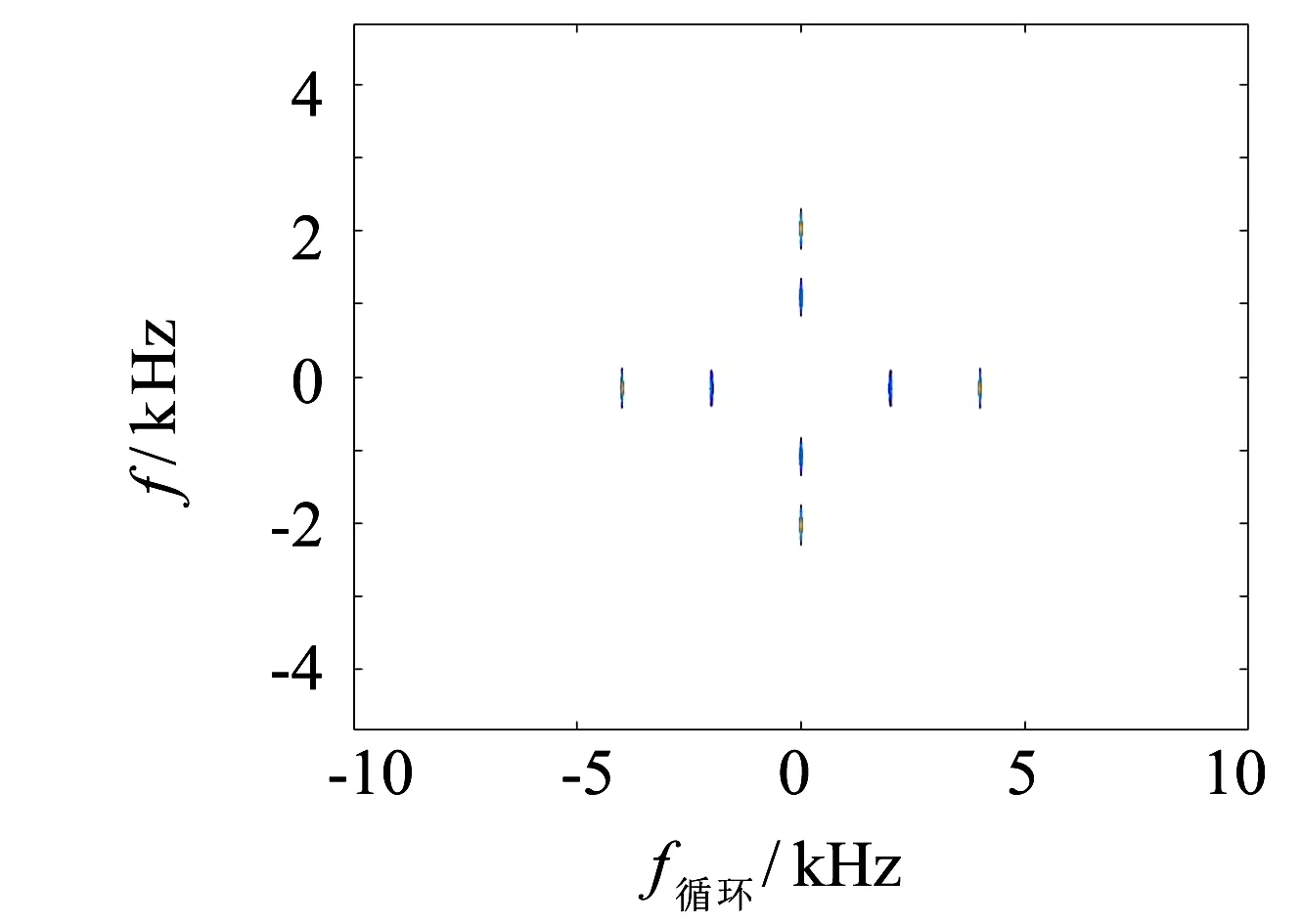
(a) 2FSK

(b) 4FSK

(c) BPSK

(d) QPSK

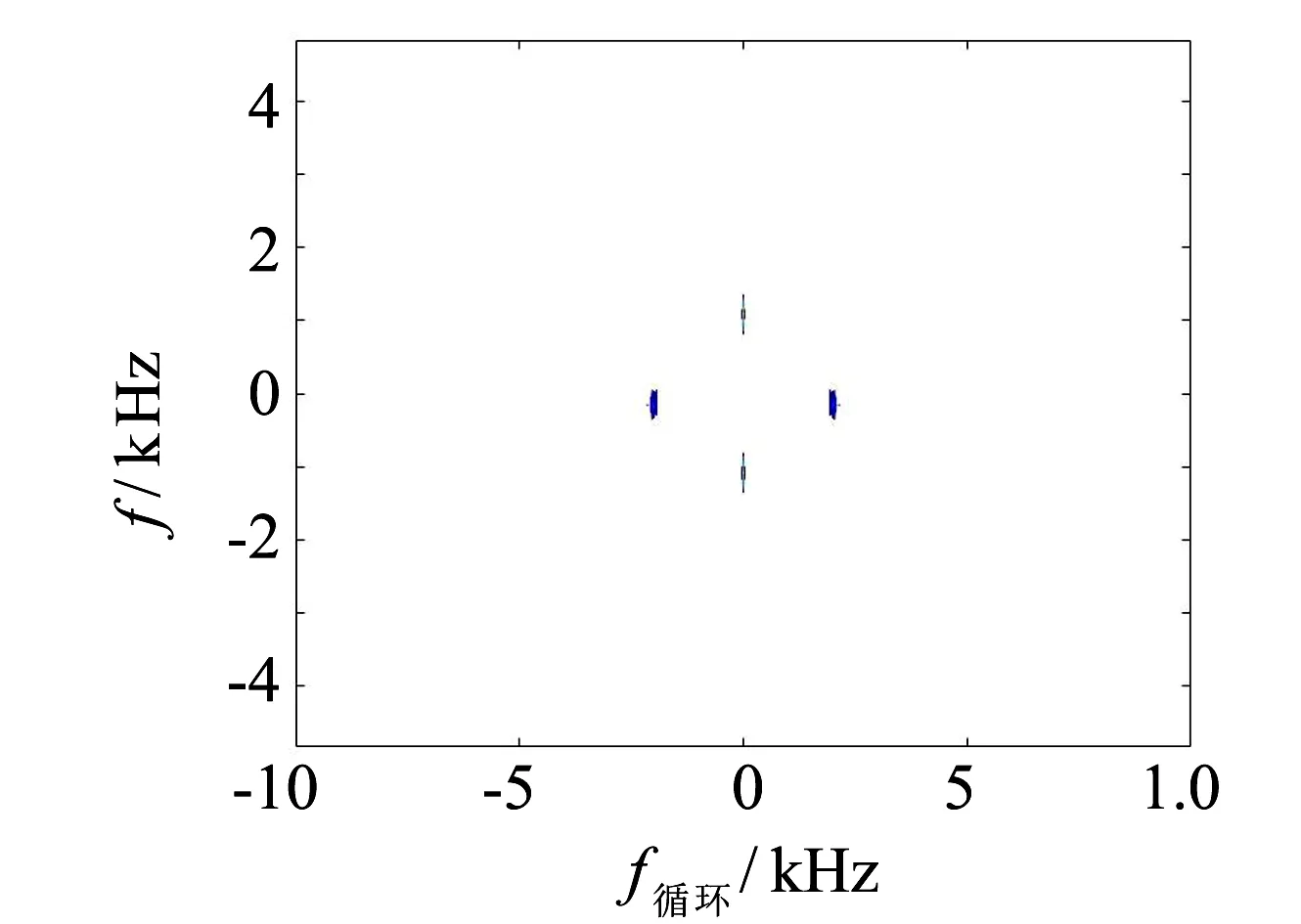
(e) 16QAM

(f) 64QAM

最后对生成的循环谱特征图裁剪去除边缘冗余信息， 然后将其做二值化处理， 生成CNN的输入图像， 关于CNN的搭建将在下节给出.

2 基于CNN-SVM的调制方式识别

2.1 CNN网络的搭建

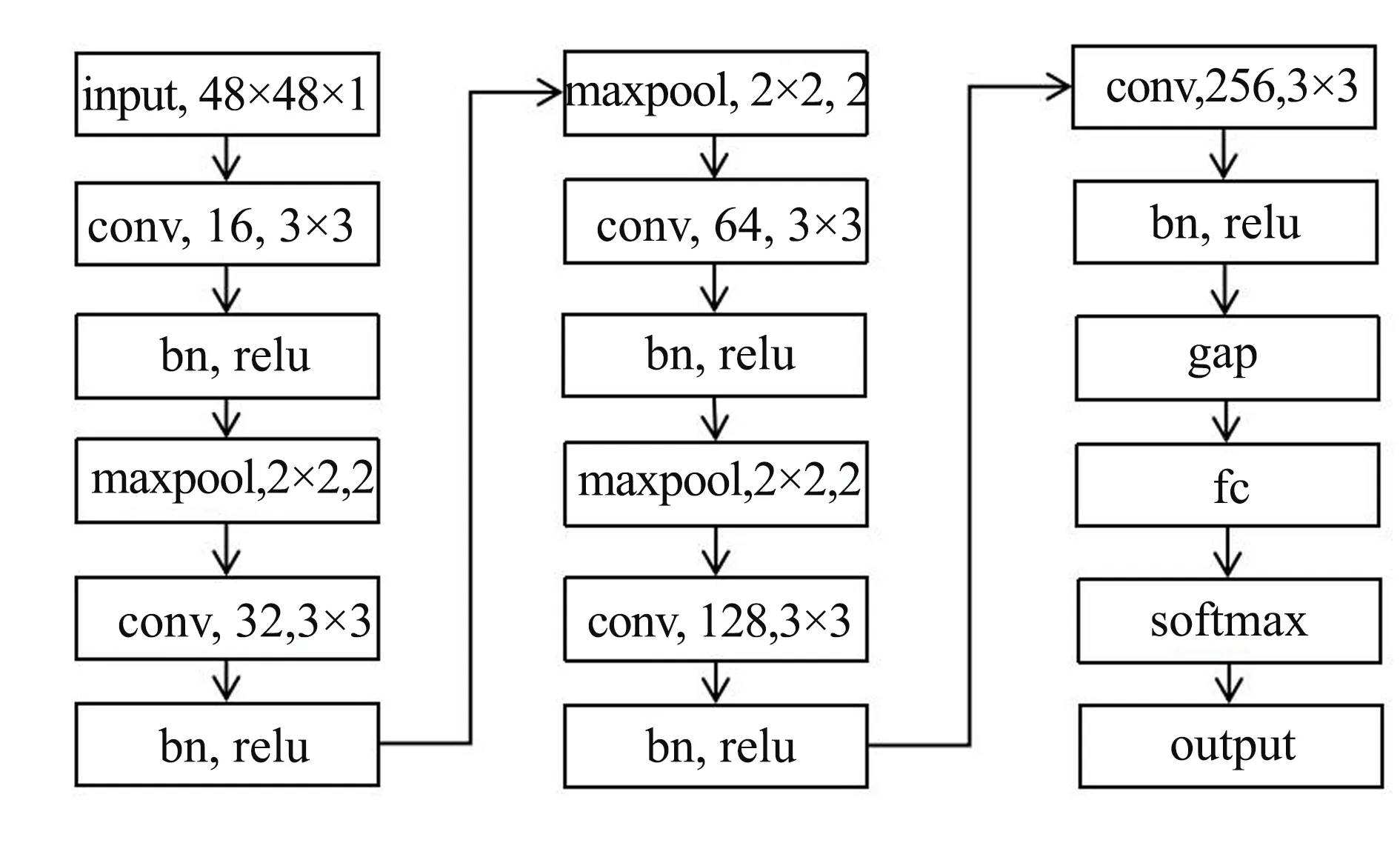
图2 CNN网络结构Fig.2 Structure of CNN network

卷积神经网络由于其在特征提取方面有着卓越的表现， 被越来越多地应用在图像分类识别领域. 本研究搭建23层CNN网络用来提取循环谱特征值. 具体的网络结构图如图2所示. 图中: conv代表卷积层， 其步长皆为1. maxpool代表最大池化层， 步长为2， bn为标准化层； relu为激活函数层; gap(global average pool)为全局平均池化层， fc为全连接层; softmax为分类层; output为输出层. 本研究使用SVM作为分类器， 因此训练数据无需经过fc及以下几层， 直接从gap提取所需要的循环谱特征值.

2.2 t-SNE降维

因为在CNN中， 从gap层提取出的特征值是高维的， 故采用t分布邻域嵌入算法(t-SNE)降维技术降低特征值的维度， 通过降低高维特征值的维度来减少后续的计算， 并且还能进一步地提取特征值.t-SNE是一种高效的降维算法， 是由SNE发展而来， 其主要思想是构建相似目标之间的概率分布. 具体算法实施如下：

对于高纬输入数据x1,x2, …,xN， 输入之间相似的条件概率：

(11)

(12)

设定Qj|i=0， 代价函数为：

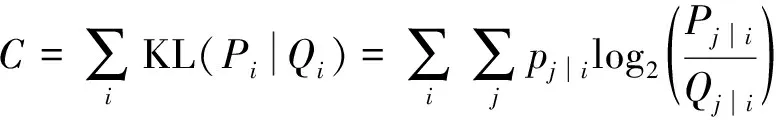
(13)

根据t分布的对称性， 则代价函数可以改写为：

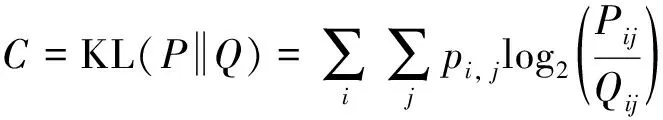
(14)

并且有Pij=Pji,Qij=Qji， 因此式(11)～(12)可以改写为：

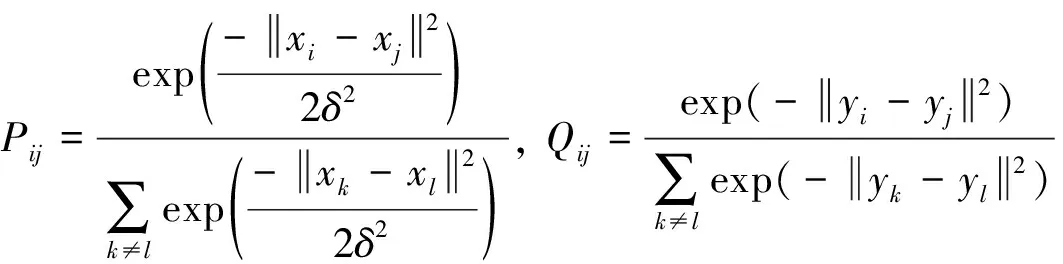
(15)

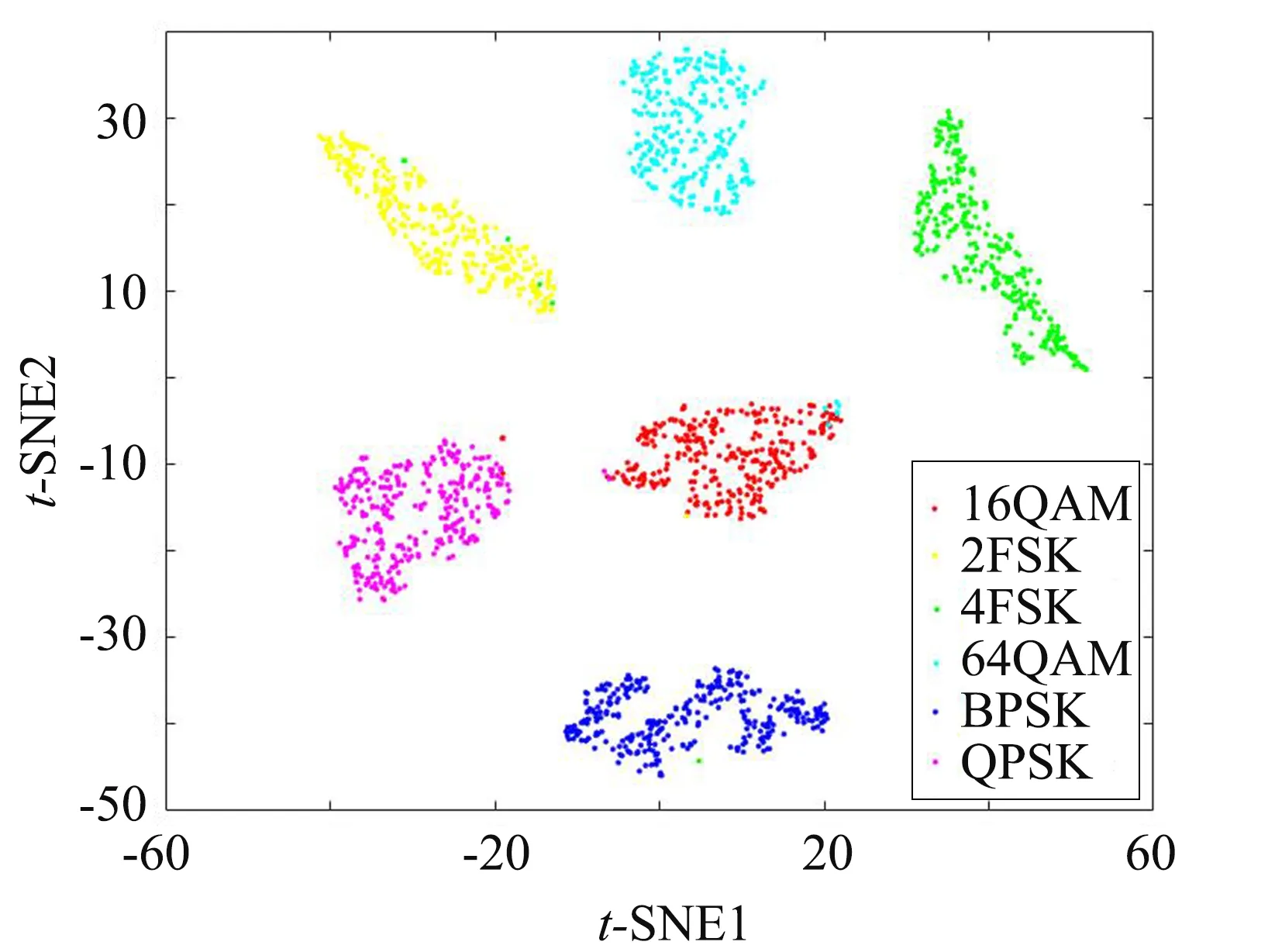
图3 特征值聚类图Fig.3 Clustering graph of eigenvalue

由CNN中gap层提取出的特征值， 经t-SNE降维， 聚类情况如图3. 可以很直观地看出， 六种已调信号根据其特征值被划分到6个不同的区域. 以下将给出SVM的设计.

2.3 SVM分类器的设计

SVM很擅长处理非线性的分类问题， 并且有着不俗的分类表现， 因此本研究算法采用SVM作为最终的分类器. SVM算法的主要思想是找到一个最大间隔超平面使得需要分类的对象离这个平面的距离最大， 分离超平面为

wx+b=0

(16)

具体步骤如下：

1) SVM的输入可以用如下的集合表示.

T={(x1,y1), (x2,y2), …, (xN,yN)}

(17)

其中:xi∈Rn，yi∈{+1, -1},i=1, 2, …,N，xi为第i个输入，yi表示每个输入对应的类别.

2) 选择高斯核函数.

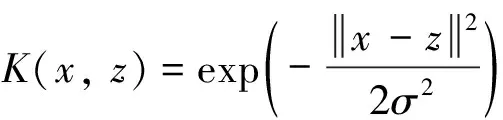
(18)

3) 构造求解凸二次规划问题.

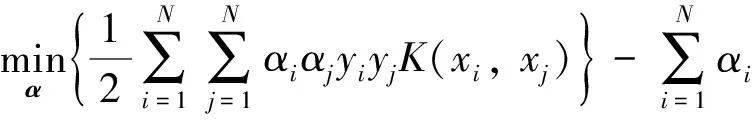
(19)

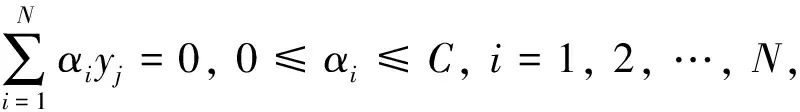
4) 计算b*.

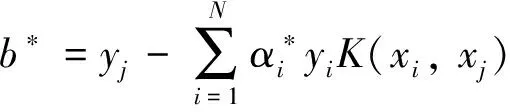
(20)

5) 计算w*.

(21)

6) 输出分类决策函数.

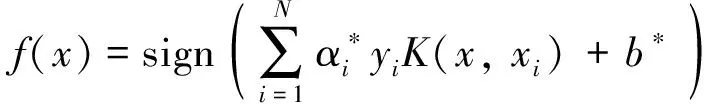
(22)

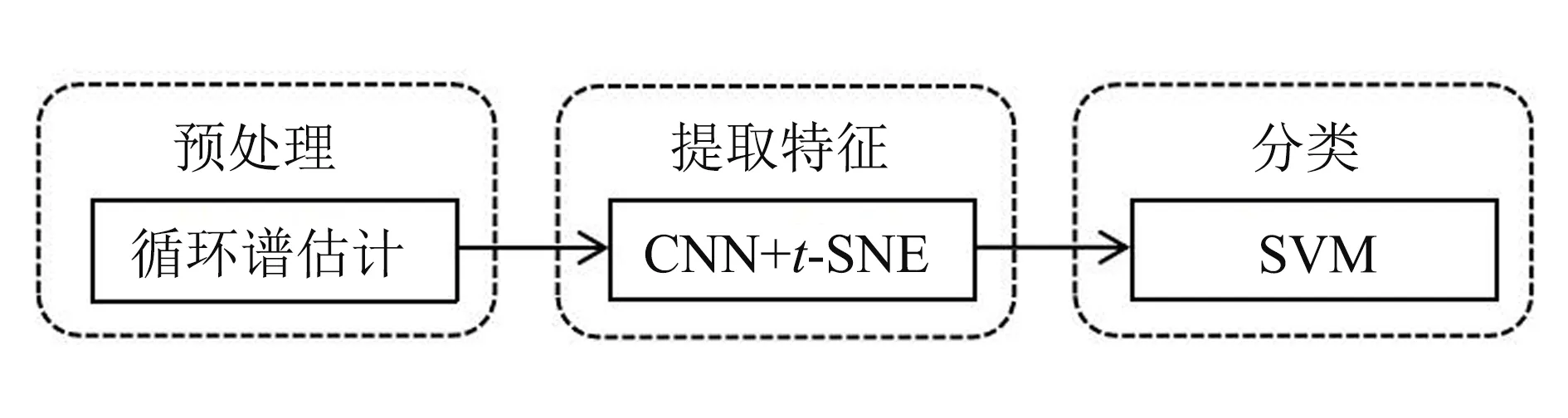
图4 算法流程图Fig.4 Flow chart of the algorithm

则整个分类模型的设计流程为： 输入图像数据经CNN网络训练， 提取gap层输出的特征值， 将提取到的高维特征值采用t-SNE降维处理， 经CNN+t-SNE处理后得到的特征值作为SVM的输入数据进行训练， 最终得到CNN-SVM分类器， 整个调制方式识别流程框图如图4所示.

3 仿真实验

3.1仿真实验及结果分析

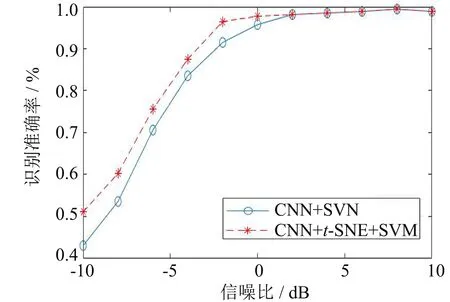
图5 整体识别率随信噪比的变化Fig.5 Change of overall recognition rate with SNR

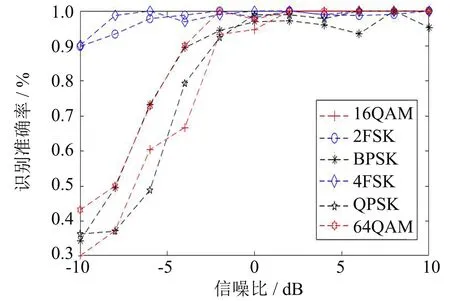
图6 不同已调信号识别率随信噪比的变化Fig.6 The change of recognition rate of different modulated signals with SNR

针对BPSK， QPSK， 2FSK， 4FSK、 16QAM、 64QAM六种已调信号， 令载波频率fc=1 kHz， 抽样频率fs=10 kHz， 采样数N为2 048， 平滑窗M取64， 信噪比取值范围为从-10 dB到10 dB， 每2 dB取一组做实验， 共11组， 对上述六种已调信号添加随机噪声， 然后再进行循环谱计算. 每种已调信号每信噪比生成300张循环谱特征图， 一种信噪比下共有1 800张图， 输入到CNN+t-SNE特征提取器中提取特征， 取其中70%的特征提取器的输出结果作为SVM分类器所需要的训练数据， 剩下的30%用来测试结果. 并与CNN+SVM(未加t-SNE)作比较， 经实验仿真， 本研究所提算法整体识别率变化如图5所示.

分析实验结果， 由图5可以看出， 当信噪比低于0 dB时， 本研究所提算法在识别率方面高于未添加t-SNE时CNN+SVM的算法， 当信噪比在0 dB以上， 两种算法的识别率基本相同. 并且可以看出， 在信噪比高于-2 dB时候算法识别准确率稳定在96%以上， 表明了该算法在低信噪比的条件下依然具有很好的识别效果.

不同已调信号的识别率随着信噪比的增加而增大(图6)， 在信噪比高于-2 dB时， 六种已调信号的识别率都保持高于90%. 因此验证了该算法提出对于提高低信噪比环境下分类识别的有效性.

3.2 算法比较

文献[9]提出利用欠完备自编码器对已调信号提取特征并利用三层全连接层神经网络来作为分类器进行识别的算法. 文献[10]提出利用高阶统计量的特性， 构造特征参数， 并采用SAE-softmax网络进行调制分类的方法. 取信噪比从0到10 dB， 间隔2 dB， 共6组信噪比， 分别将每组信噪比下本研究所提算法与文献[9-10]所提算法的分类识别率进行对比， 结果如表1所示:

表1 各算法识别率对比

由表1各算法的比对结果可以看出， 本研究所提算法在识别率上高于文献[9-10]所提算法， 并且由于文献[9]使用的欠完备自编码器是全连接的网络结构， 参数较多， 学习复杂度较大. 并且其局部参数的调整很容易影响到整体结构的参数调整， 造成模型不稳定， 因此鲁棒性较差. 而卷积神经网络采用的是局部连接结构， 达到参数共享， 因此所需参数较少， 并且相比全连接结构参数更易于调整. 相比较下， 卷积神经网络比欠完备自编码器更容易处理图像且识别率也更好. 故本研究所提算法相比文献[9]计算效率更快， 模型更具鲁棒性. 文献[10]采用高阶累积量对信号做预处理， 并且其使用的堆叠自编码器同样存在参数较多及模型鲁棒性较差的问题， 由于本研究采用的是二阶循环谱计算， 因此， 相比之下计算量就更少.

4 结论

将CNN和t-SNE结合起来作为特征提取器， 结合SVM优越的分类性能， 设计出分类模型， 将整个分类模型各个模块细化， 方便不同模块的修改变更以及整个模型的优化调整， 可拓展性和发挥空间更大. 本研究提出的算法是基于循环谱和卷积神经网络的调制识别算法， 首先对BPSK、 QPSK、 2FSK、 4FSK、 16QAM、 64QAM这六种已调信号进行谱平滑周期图法计算循环谱， 截取循环谱等高图做裁剪、 二值化操作， 然后输入到CNN进行特征提取， 对于CNN中gap层提取到的特征值采用t-SNE降维， 最终输入到SVM进行训练、 分类识别. 实验结果验证了该算法相比于其他算法， 在低信噪比的环境下有更好的识别准确率.