基于主元分析的电磁继电器贮存失效机理研究

李维燕,王召斌,陈康宁,李 朕,王 占,尚 尚

(江苏科技大学 电子信息学院,镇江 212100)

航天继电器、弹用、军用继电器等特殊用途的继电器,是导弹武器系统的关键器件,承担着系统控制与保护等重要的功能,在和平与发展的年代,导弹武器会长期处于贮存状态,其所用继电器也将处于贮存状态,因此,研究这类继电器的贮存可靠性具有重要的意义[1]．

电磁继电器在贮存过程中,各方面性能会随着贮存时间的延长不断退化,可能出现多种不同的失效模式,表现为不同参数的退化．产品的失效是不同退化模式间竞争的结果,任何一个参数超出阈值都可能使继电器失效,且由最早达到失效阈值的退化参数决定[2]．

通常用加速贮存实验获得的敏感参数来分析继电器性能的变化．继电器贮存退化过程中可能会存在多个与性能有关的敏感参数,目前大多数学者基于单一参数建模,如文献[3]以接触电阻为敏感参数,采用Bayes方法对继电器的可靠性进行评估；文献[4]分别以接触电阻和吸合时间建立模型；文献[5]以接通时间、断开时间以及接触电阻建立模型,但仅仅用一两个敏感参数建模分析其可靠性可能会忽略掉很多重要信息[6-7]．因此,为了使继电器的贮存可靠性分析更加准确,文中提出了基于主成分分析的贮存退化数据分析方法，在继电器进行加速贮存实验的基础上,确定继电器的失效模式,以及退化的敏感参数,通过相关性分析判断敏感参数之间的相关性，并对各敏感参数进行主元分析,选择最能表征继电器失效模式的主元进行可靠性分析．

1 继电器加速贮存实验及实验结果

1.1 加速贮存实验

取某型超小型中功率熔焊密封直流电磁继电器为实验研究的对象,该继电器产品具有二组自动转换触点,体积小,重量轻,工作可靠,适应各种环境变化,可广泛地适用于航天、航空、导弹武器控制等多种领域．其整体结构如图1．

图1 实验继电器结构

记录其在特定的贮存条件下电参数漂移情况,观察其触点以及簧片表面情况,结合可靠性、材料、机械、力学等方面知识,利用加速试验平台和参数测试平台,研究相应参数退化规律及机理,采用适用的数据分析方法评估继电器贮存可靠性，实验流程如图2.

图2 加速贮存实验流程

在温度,湿度以及振动等环境应力中,温度是影响继电器贮存可靠性的主要因素,因此以温度作为加速应力,加速贮存试验的温度应力至少为室温～180 ℃,文中选取该型试验继电器的最高工作温度125 ℃作为加速试验的最低环境应力,同时充分考虑高温的作用,选择210 ℃作为最高环境应力,中间的两个温度根据GB2689.1中的规定,按照温度应力倒数等间隔选取，设置125 ℃、150 ℃、175 ℃和210 ℃ 4个温度等级,分别对40支电磁继电器进行了为期180 d的加速退化实验,以9 d为一个周期测试继电器各项参数,获得20个周期的退化数据以及失效情况．

1.2 继电器加速贮存实验结果

通过统计图分析各数据的退化趋势,其中线圈电阻和接触电阻分别随贮存时间及温度应力的增加而呈现不断减小和增大的趋势,为敏感参数．动作电压和释放电压具有随贮存时间及温度应力的增大而缓慢降低的趋势,为敏感参数．时间参数中的释放时间具有随时间及温度应力的增大而缓慢上升的趋势,为敏感参数,动作时间整体变化趋势不显著,退化不敏感．继电器动作回跳时间、释放回跳时间和同步差的波动性较强,贮存过程中变化的随机性很大,趋势性不强,故不作为敏感参数．实验数据如图3,只给出敏感参数在4个温度应力下的趋势图,其中210 ℃时,后期接触电阻严重超标,影响其他3个温度下接触电阻退化趋势观测,故在趋势图中并没有将其做出．

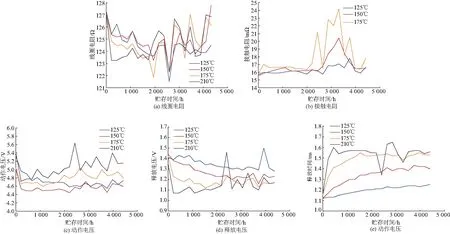
图3 敏感参数趋势

退化数据是加速贮存实验获得的,进行可靠性分析的主要依据,其中能够表征贮存失效的参数应该有明确的物理意义,能够反应继电器贮存过程性能的退化,容易测量且相对于贮存时间有较为明显的变化趋势．上述参数都满足性能存在不可逆的退化过程与退化具有可加速性这两个特征．综上所述,可以将实验继电器的接触电阻、动作电压、释放电压和释放时间作为贮存退化实验中的敏感参数,为下一步产品性能与时间的关系展开进一步研究．

2 贮存失效机理

继电器在贮存过程中,不会有电效应,其性能的退化都是缓慢的物理化学变化[8](如氧化、腐蚀、气氛变化、结晶、磨损、应力松弛等)．本次加速退化试验的继电器均为平衡衔铁式1/2结构,属于晶体罩系列,其动作过程为:当继电器线圈加电压激励后,电磁系统通电产生电磁吸力,吸引衔铁向轭铁靠近．当加在线圈上的电压激励达到一定值(动作值),相应的电磁吸力足以克服继电器机械系统产生的弹簧反力时,衔铁被吸引与轭铁紧贴．与此同时,与衔铁相连的推动杆推动动簧片与常开静簧接触,从而接通被控电路．线圈断电后,电磁吸力随之消失,弹簧反力推动衔铁回到原来的位置,动簧片与常闭静簧接触,触簧系统回到原始状态,继电器完成一次动作转换过程．

2.1 继电器接触失效机理

加速贮存实验中样品失效情况如表1,在贮存实验过程中,有少量样品出现失效,表现为接触电阻超标、触点不导通和正弦振动去激励抖断3种失效模式．且失效大部分发生在210 ℃温度应力下．观察图3中数据的变化趋势,可以看到个各数据在大约2 500 h时出现一个突变,且在210 ℃较为明显,一方面不排除误差的因素,由于取的是10支继电器平均值,10个数据的变化共同影响了平均值;另一方面是由于此时部分样品已经出现了失效,所以造成参数突变,而相对较高的温度使得这种变化更为明显,表明一种失效模式不止影响单一参数的退化．

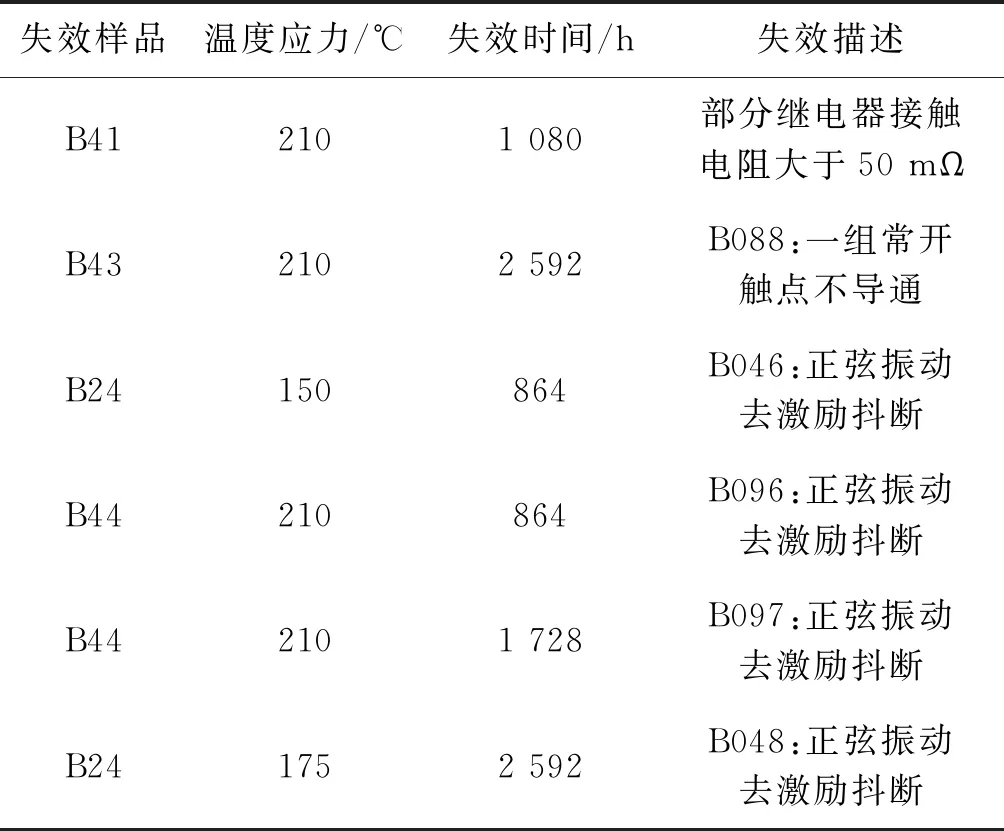
表1 样品失效情况

根据该系列继电器结构特点,在不考虑设计缺陷的前提下,其发生接触电阻超标(触点不导通)以及正弦振动去激励抖断的故障树如图4．

图4 继电器失效模式故障树

由故障树列出的末端因素逐一分析,得到触点表面腐蚀的失效机理为:① 簧片表面受氧化和有机腐蚀;② 继电器静合压力变小,导致簧片接触点的收缩电阻变大．温度应力大小和贮存时间长短均对接触电阻存在影响温度对于触点促进作用,温度应力越高,接触电阻的增长速率越高,且波动也相对越大．造成继电器正弦去激励抖断的原因为:高温贮存后触点静合压力减小,使得簧片谐振频率降低,高频振动下发生抖动．

电磁继电器贮存过程触点随贮存时间的退化都反映在接触电阻的变化上．随着贮存时间延长,触点表面受氧化和有机腐蚀出现氧化物的增长和堆积,温度应力通常能加速氧化物的产生．继电器接触电阻超差是影响其贮存可靠性的主要的因素之一．触头所处气氛复杂,在这些气体作用下触头表面会形成腐蚀膜或氧化膜,影响触点导电性,使得触点实际接触区域减小,造成接触电阻增加,当腐蚀绝缘膜覆盖整个触点表面时,就会出现触点不导通失效．

文献[4]运用SEM实验以及EDX分析的手段对触点进行了微观分析,建立了温度应力下基于接触电阻性能退化的继电器贮存可靠性模型．

2.2 继电器簧片应力松弛失效机理

2.2.1 电压参数变化原因

继电器的动作电压(电流)指的是能够使继电器动作的最小电压(电流)．除表1出现的失效情况外,动作电压和释放电压都有缓慢的下降趋势,需要探究电压参数下降的原因．通常情况下,继电器动作电压主要受到初始复原反力、触点静合压力、触点间隙和超行程的影响．释放电压主要受超行程、初始复原反力的影响．通过对贮存前后线圈电阻的测量,发现线圈电阻均呈缓慢下降趋势,如图3(a)以及表2,可以看出线圈电阻前几个贮存周期后出现了显著的下降,且最大的下降幅度不超过2%,而后又缓慢上升至靠近初始值,该变化趋势与测试的环境温度相关．故电磁只是在前几个贮存周期略微上升．

表2 线圈电阻退化情况

通过图3中(c)和(d)动作电压和释放电压的退化趋势可以看出,4个不同温度应力下的动作电压和释放电压均在首个周期都呈现整体大幅度下降,之后的19个周期趋于稳定．210 ℃温度应力下在首个贮存周期下降趋势最为明显,动作电压均值下降0.8 V左右,释放电压均值下降0.3 V左右．

同时,通过继电器贮存前后机械参数的测量,图5为150 ℃温度应力下触点静合压力与复原反力的趋势图,其他3个温度应力具有相同的趋势,可见触点静合压力和初始复原反力在首个贮存周期后均出现显著下降,之后下降趋势减缓,触点静合压力、初始复原反力与动作电压、释放电压的下降趋势相同．因触点间隙和超行程在整个试验过程中基本保持不变,故继电器动作电压和释放电压的变化主要受到静合压力和复原反力大小的影响．在贮存退化试验条件下,继电器动簧变形处应力松弛效应是造成静合压力变小的主要原因,试验前期簧片(动簧、复原簧)应力释放较为明显,故静合压力和复原反力的变化也较为明显,之后应力释放趋于稳定,静合压力和复原反力的变化也趋于平缓．因此,可以认为动簧变形处的应力松弛是造成继电器电压参数减小的主要原因．

图5 150 ℃贮存条件下机械参数变化趋势

电磁继电器长期贮存时,其电磁系统、触簧系统以及机械系统均会发生一定程度的退化[9],从而影响继电器的正常工作特性．由于继电器动作特性的影响因素众多,文献[8]摸底试验综合分析比较各影响因素,认为簧片的反力特性变化对继电器接触特性影响最大．继电器的簧片本身具有一定的弹力,可保证触点可靠接触．但继电器贮存时,簧片材料会发生应力松弛,导致簧片提供的反力减小,继而影响吸反力的配合,进而影响接触过程．

随着簧片材料的应力松弛,其弹簧反力将会随之下降,为维持吸反力的配合,则需要吸力相对下降补偿反力的下降以维持吸反力的配合,而在上述分析中已经知道线圈电阻下降趋势并不明显,电磁吸力只略有上升,那么只有电压参数的下降能使电磁吸力下降补偿应力松弛造成的反力下降．当应力松弛达到不可补偿的地步时,继电器失效．

2.2.2 时间参数变化原因

图3(e)为继电器在加速贮存退化试验中释放时间随测试时间退化的整体趋势．通过释放时间的退化趋势可知,125 ℃、150 ℃温度应力下继电器释放时间呈现缓慢上升趋势;175 ℃、210 ℃温度应力下继电器释放时间先显著上升,然后趋于稳定．继电器的释放时间取决于复原反力、超行程、触点间隙和静合压力,从上述分析已知继电器的触点间隙和超行程基本保持不变,故继电器释放时间主要受到继电器返回力(含触点压力和复原反力)变化的影响．在贮存退化试验条件下,继电器动簧和复原簧折弯处的应力松弛效应造成静合压力和复原反力变小,从而对释放时间产生影响．

研究发现在贮存过程中,继电器接触电阻、动作时间以及释放时间的变化对其贮存寿命与可靠性的影响最为显著．继电器的动作时间由吸合过程决定,吸合过程取决于触簧系统与电磁系统的相互配合,应力松弛导致动簧片在吸合过程中运动行程减小,同时动簧片机械反力减小,都将导致动作时间减小．但通过加速贮存实验实测数据,动作时间退化趋势并不明显,因此，不能将动作时间作为应力松弛机理的表征参数．

继电器释放时间主要受到反力的作用,应力松弛现象导致动簧片和静合静簧片之间的接触力减小即反力减小,继电器在释放过程中动簧片运动加速度减小,释放时间增大．通过分析加速贮存实验数据发现,释放时间变化较为明显,且随时间逐渐增大．温度越高,释放时间退化越大,退化趋势也越明显．

如图6和图7,当簧片反力在贮存过程中减小时,电磁吸力与机械反力的合力增大,动作电压(或释放电压)减小时,图7中各电压参数对应的的吸力曲线会降低,当动作电压减小到一定程度,其对应的吸力可能会小于反力,该动作时不动作,或者释放电压对应的吸力大于反力,该释放时没有释放,导致继电器动作错乱失效．

图6 电磁继电器接触系统示意

图7 典型的吸反力特性曲线

簧片材料一开始承受弹性变形,但随着贮存时间延长,簧片在持续的温度应力下,由于晶界的扩散及晶粒内部亚晶的运动使弹性变形不断转化为塑性变形,使得应力随之减小．图8为各贮存时段内动簧片的金相分析图,从图中可知簧片的晶粒随贮存温度的增加而增大．

图8 不同温度应力下动簧片晶粒

综上所述,动簧变形处的应力松弛机理与线圈电阻、动作电压、释放电压以及释放时间等参数都有关．

3 各退化模式间相关性分析

实际情况下,各个退化参数彼此之间可能相互影响,存在着一定的相关性．关于两种失效数据间的相关性,即一种失效数据退化时另一种失效数据总是伴随着一起退化,说明两退化数据是相关的,相反则是无关的．在上述实验中,动簧变形处的应力松弛机理与线圈电阻、动作电压、释放电压以及释放时间等参数都有关,这些参数之间是否有某种关联，需要用数学的方法进行进一步的探究．在实际退化过程中,若同一失效机理同时存在多个退化敏感参数,产品的寿命往往取决于最先达到失效阈值的退化数据,这个过程如图9．

图9 多敏感参数退化

判断各退化数据之间的相关性，其检验通常有:协方差矩阵法、Pearson相关系数法、Kendall相关系数法以及Spearman相关系数法等[8]．协方差矩阵用于计算相关性具有简单、便捷的特点．在不判断变量是否符合正态分布的情况下,文中选择协方差矩阵法判断两种退化数据的相关性，其方法为:在t时刻一个简单样本的两个退化数据x1(t)和x2(t)，如果它们是相关的,则下式成立:

P{x1(t)≤D1|x2(t)≤D2}≠

P{x1(t)≤D1}P{x1(t)≤D1，x2(t)≤D2}≠

P{x1(t)≤D1}P{x2(t)≤D2}

(1)

已知其协方差cov(x1(t),x2(t))≠0,反之亦然．可得推论:任意两个退化数据xi(t)和xj(t)之间的关联程度用协方差的值来判断,协方差越接近于0，相关性越小;协方差越接近1，则相关性越强．

任意两退化数据之间的相关性都可以用式(2)协方差矩阵来评估,其中的协方差可以用式(3)计算.

(2)

cov(xi(t),xj(t))=

E[xi(t)-μxi(t))(xj(t)-μxj(t))]=

(3)

式中：μxi(t)为xi(t)的均值向量．

文中选取继电器的释放时间作为衡量继电器贮存寿命的主要预测因子．而线圈电阻、动作电压、释放电压这些变量可能会间接影响释放时间的变化．根据协方差矩阵法来确定任意两组数据之间的相关性．用数学软件相关函数进行计算,将4个变量进行相关性分析得到表3．

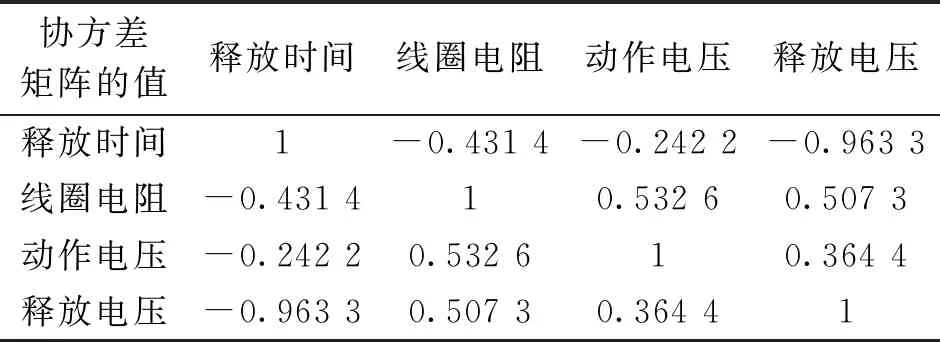
表3 相关性分析

相关系数在0.00～±0.30之间为微相关;±0.30～±0.50之间为实相关;±0.50～±0.80之间为显著相关;±0.80～±1.00之间则为高度相关[10]．

由表3可以看出,线圈电阻、释放电压的相关性比较明显,尤其是释放电压对释放时间的影响较大,但动作电压、释放电压与线圈电阻特征量序列的相关程度也已经达到了显著相关,有必要进行主元分析,消除原始变量的冗余信息．

4 多退化数据主成分分析

电磁继电器敏感参数退化规律反应继电器失效模式的特征．然而应力松弛机理与多个退化参数有关,若仅用一两个敏感参数进行预测又过于武断，因此运用主成分分析法处理多维退化数据,对数据进行降维处理,使贮存可靠性分析更为准确．

将与应力松弛有关的敏感参数数据进行主成分分析,尽可能多地综合原始数据的重要信息,得到原始数据的特征信息[6](第一主元和第二主元),再用主成分代替原始变量进行可靠性分析,其流程如图10．

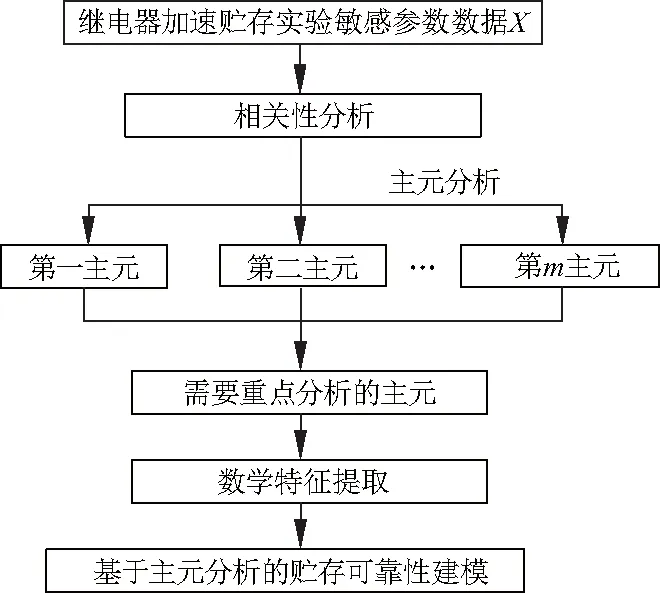
图10 基于主元分析的可靠性分析流程

主成分分析(主元分析)能够实现数学降维,用数学方法得到几个新的变量来代替原来众多的变量,达到降维的目的,这几个新变量彼此之间互不相关,并且尽可能地综合原来变量的信息．

对于原始数据矩阵Xm×n,其列向量xi为一个敏感参数的特征矢量,其行向量为各参数观测样本,可表示为:

(4)

式中：ti(i=1,2,…,m)为得失分量,pi(i=1,2,…,m)为负荷分量．ti和pi都是两两正交的．X在与得分矢量相应的负荷矢量方向上的投影[11],即为主元,可表示为:

ti=Xpi

(5)

实质上对X的协方差矩阵进行特征向量分析即为矩阵X的主成分分析．

在实际应用中,X的特征矢量通常量纲不同或数量级差别较大,此时可以先对其进行标准化处理再进行主元分析,按照式(6)进行计算,使X的特征矢量均值为0,方差为1．

(6)

标准化后得到矩阵Y,其协方差矩阵为:

(7)

保留加速贮存试验获得的所有敏感参数,有利于更加准确、全面地剖析继电器贮存性能的退化．但加速贮存试验结果表明,因受多种因素共同影响,同种失效机理下各敏感参数的退化往往呈现较复杂的规律,并不是单纯的递增或递减．考虑到多维退化参数之间存在一定的相关性,而主元分析方法不需要进行数学模型就能最大限度综合原始数据的相关信息[11],因此采用主成分分析法对原始多维退化参数降维,综合各特征量的相关性．将与应力松弛有关的线圈电阻、动作电压、释放电压以及释放时间退化数据作为原始数据源构成数据矩阵Xn×4,其中n为测试周期．对X进行主元分析,得到各主元ti(i=1,2,3,4)并计算各主元的贡献率．表4为计算得到的所有失效样品第一主元、第二主元贡献率以及一二主元累计贡献率．

表4 样品各主元贡献率

从表4可看出,样品各温度应力下第一、二主元累计贡献率已超过80%．换言之,前两个主元已能较强地综合原始数据所包含的性能变化信息．其中第一主元用原始数据表示为：

Y125℃=-0.482 5X1-0.531 3X2-0.444 5X3+0.533 6X4

Y150℃=0.469 6X1+0.380 6X2+0.579 3X3-0.546 8X4

Y175℃=0.398 0X1+0.347 4X2+0.634 3X3-0.564 4X4

Y210℃=0.391 3X1+0.548 4X2+0.567 9X3-0.472 8X4

(8)

得到应力松弛机理下各退化参数的第一主元和第二主元如图11．线圈电阻、动作电压、释放电压、释放时间的退化都和簧片应力松弛密切相关，即4个参数都包含了与簧片应力松弛有关的信息,而第一主元的贡献率最大,综合了原始数据绝大多数的相关性,反映了簧片的应力松弛．

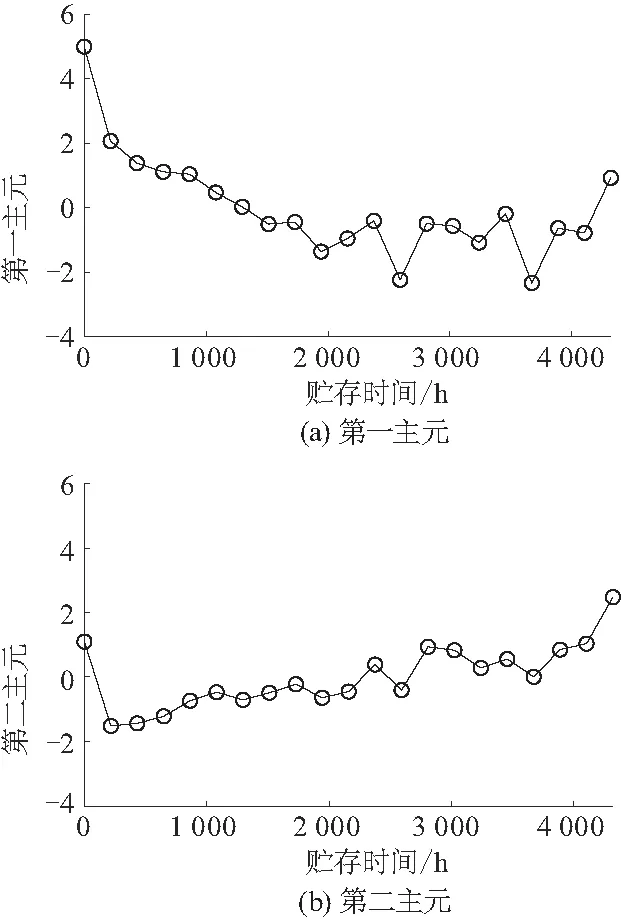
图11 150 ℃第一、第二主元变化规律

第二主元体现原始数据与第一主元之间的误差信息,第二主元越小,则原始数据与第一主元的误差越小,参数退化的随机性越小,干扰因素越少,主成分分析结果越好．其他主元贡献率较小,可以忽略．从图11可以看出,第一主元变化趋势说明簧片应力松弛造成的参数变化呈减小趋势．第二主元幅值较小,说明退化参数变化受簧片应力松弛变化影响明显,相关性较强,干扰因素少．即原始多维退化参数经主成分分析之后,更清晰地反映了继电器应力松弛情况．

典型的应力松弛曲线如图12,可以看出应力松弛主要分为两个阶段,即应力先显著下降后缓慢下降．

图12 典型的应力松弛特性曲线

如图12中曲线1,在应力松弛过程的初始阶段,应力下降较为明显,而后下降趋势变得平缓,这与图11中第一主元两段式下降趋势相吻合,即反力变化与第一主元的变化是同方向的．如果能够证明反力与第一主元的变化存在某种线性关系,则可认为原始数据经主元分析得到的第一主元能直接反映应力松弛造成的反力变化．

5 结论

(1) 运用电磁继电器加速贮存实验系统进行了为期180 d的加速贮存实验,得到线圈电阻、接触电阻、动作电压、释放电压、释放时间等敏感参数．

(2) 基于敏感参数退化规律,分析各参数退化的原因,以及继电器贮存过程中的应力松弛机理,并进行各数据相关性分析．

(3) 在应力松弛引起了多个参数退化的前提下,运用主成分分析的方法,将多个参数用最能反应原始数据退化信息的主元代替．主元分析结果显示第一主元与应力松弛曲线有相同趋势,后续还可以采用实验与仿真的方式验证这种关系．

文中的贮存退化数据分析方法适用性强,为多退化参数下继电器贮存可靠性分析提供参考,但还需实验进行后续分析,进一步对继电器进行寿命预测和可靠性评估．