外形参数对翼身融合水下滑翔机的高升阻比特性影响研究

张代雨,王志东,凌宏杰,朱信尧

(江苏科技大学 船舶与海洋工程学院, 镇江 212100)

海洋占地球表面积的71.8%,具有丰富的自然资源,世界上各国对海洋资源的开发与利用日益重视．水下滑翔机(autonomous underwater glider, AUG)[1-4]作为一种新型的水下航行器,主要通过调节净浮力来改变其运动姿态,实现在水中的滑翔运动．其对能源的需求量小,制造成本低，可以长时间在不同深度、不同广度的海域中航行,目前越来越受到各国研究人员的重视．

相较于由回转体、水翼和操纵面组成的传统布局水下滑翔机,翼身融合水下滑翔机具有翼型剖面形状的扁平机身,且水翼与机身平滑地融合在一起,可大幅提高升阻比．

但翼身融合水下滑翔机的外形曲面复杂,需要使用大量的外形参数进行描述,在水下滑翔机设计过程中若对这些参数都进行详细设计,效率不高.因此,分析各种外形参数对升阻比的影响,划分出外形主要影响参数和次要影响参数,可指导设计者进行快速设计,减少设计成本,提高设计效率．

采用试验设计方法(design of experiments,DOE)[5-6]可进行翼身融合水下滑翔机外形参数对升阻比的影响率分析,但需要对生成的每一个样本点进行相应的升阻比计算．目前,计算流体力学(computational fluid dynamics,CFD)方法为常用的翼身融合水下滑翔机升阻比计算方法[7-9],并且经过科研人员多年的努力,已开发出CFX、FLUENT和STAR-CD等多款成熟的商业CFD软件[10-13],均可应用于翼身融合水下滑翔机升阻比的精确计算．但CFD方法主要通过对流体计算域进行网格划分得到空间网格,并在空间网格上建立离散的大规模代数方程组,进而进行流体动力参数的求解,计算耗时较长,此外对空间网格(也称为体网格)的质量要求较高[14]．而使用DOE方法进行翼身融合水下滑翔机的升阻比影响参数分析时,所需的外形参数变化范围较大,无论是网格自动生成还是网格变形方法均会导致新生成的网格质量较差,不能应用于多样本点的升阻比自动计算,若手工对每一个样本点进行计算,计算时间大幅增加;此外,所需的样本点较多,由于每个样本点的CFD耗时严重,导致总的计算耗时十分严重．

针对上述问题,文中首先基于势流理论,提出一种翼身融合水下滑翔机的升阻比快速计算方法,实现外形参数大变形情况下的升阻比快速计算;然后,采用最优拉丁超立方设计进行样本采样,并建立回归模型对样本点数据进行分析;最后,得到水下滑翔机外形参数对升阻比的影响率大小排列．

1 翼身融合水下滑翔机外形参数

借鉴于航空中新一代飞行器翼身融合布局[15]的高升阻比特点,翼身融合水下滑翔机外形主要采用扁平椭球机身,且机身与机翼平滑连接,且每一个横截面均为翼型剖面．图1为11个翼型剖面组成的翼身融合水下滑翔机外形,其外形左右对称．分析图1可知,翼身融合水下滑翔机的几何外形建模主要由两类参数决定:

(1) 每个翼型剖面的形状参数．形状参数具体指的是每个展向翼型剖面所选择的翼型类型、弦长和厚度等参数．

(2) 每个翼型剖面的扭转角参数．扭转角是各个展向位置翼型剖面弦长相对于翼根剖面弦长扭转的角度,当扭转使翼型剖面前缘向下时为负值,使前缘向上时为正值．

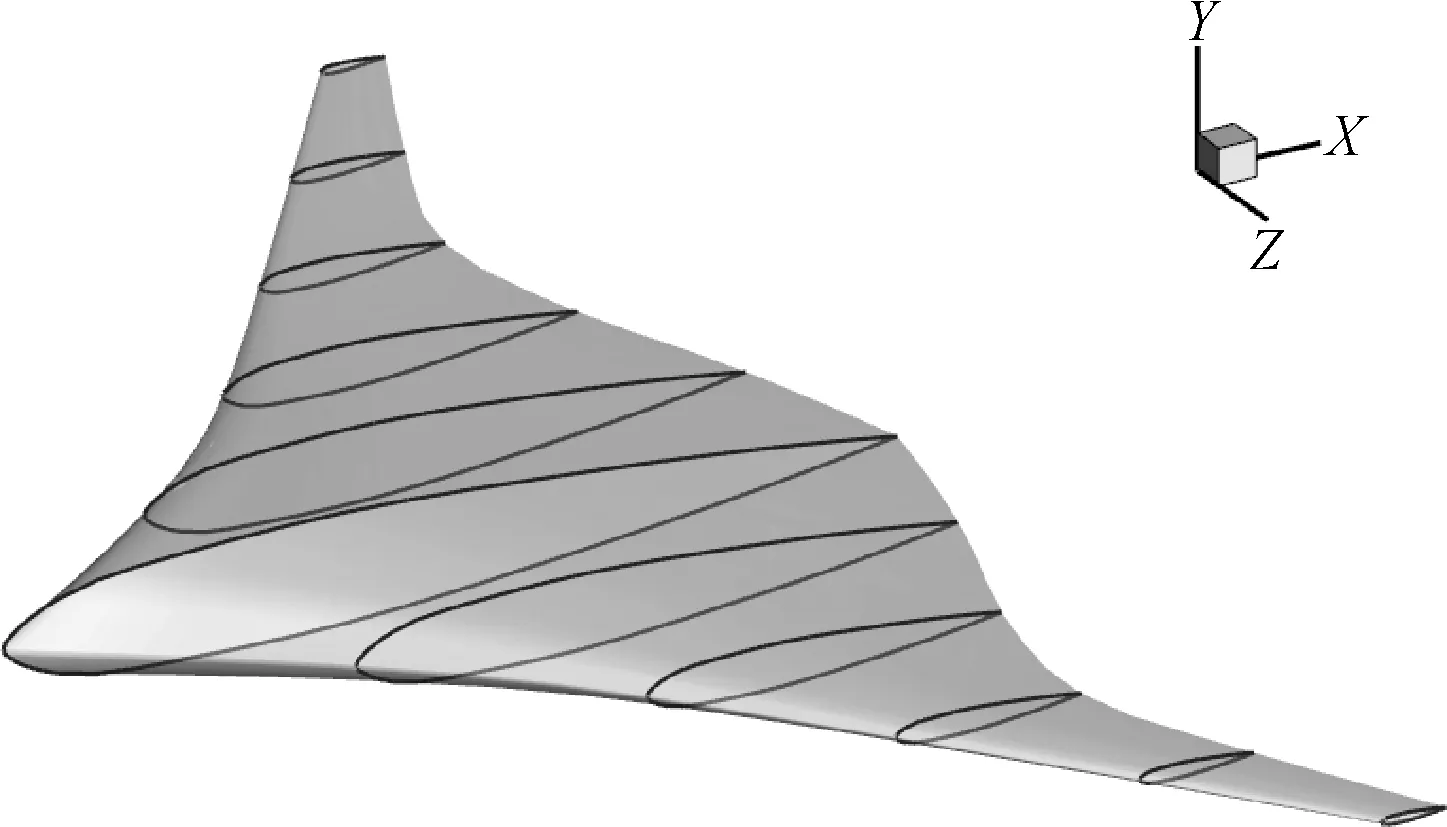
图1 翼身融合水下滑翔机外形

2 水下滑翔机的升阻比快速计算

基于势流理论,提出一种翼身融合水下滑翔机的升阻比快速计算方法,并对其进行了粘性修正．由于该方法仅需对外形表面进行离散化,因此,与CFD方法对体网格的高质量要求相比,对表面网格的质量要求大大降低,可实现外形参数大变形情况下的升阻比快速计算．

2.1 基于势流理论的升阻比快速计算

为了计算翼身融合水下滑翔机的升阻比,给定翼身融合水下滑翔机外形和相应的边界条件后,需要对外形外部的流体计算域V进行求解．如果流体计算域中的流体被认为是无漩不可压的,则控制方程为:

2Φ=0

(1)

式中Φ为速度势函数．

在滑翔机的固定体坐标系中,相应的边界条件为:

(2)

(3)

式中：n为物面边界上的法向单位向量；v为无穷远处来流速度．

基于格林公式,计算域内任一点的速度势可表示为：

(4)

式中：SB为水下滑翔机外形表面；SW为尾涡面；r为点p到外形表面上一点的距离；σ为外形表面上分布的源汇强度；μ为外形表面上分布的偶极子强度．

在式(4)中,σ和μ的分布未知,若求得σ和μ的值,则计算域内任一点p的速度势均可通过式(4)求解．因式(4)对外形表面的每一个点均成立,文中将外形表面进行离散,划分为许多小的面元,并在每个面元的中点处引入式(4)进行速度势计算,进而得到一组线性代数方程组:

i=1,…,N

(5)

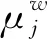
(6)

式中：Sj和Wj分别为水下滑翔机外形上的面元和尾涡面上的面元．

求解方程式(5),可得到σ和μ值．然后,基于伯努利方程和Trefftz平面法可求得水下滑翔机外形的压力分布和诱导阻力,进而可实现升阻比的快速计算．

2.2 考虑粘性的升阻比修正

求解的无粘流场可以用以计算精确的诱导阻力,但不能计算水下滑翔机受到的粘性阻力,需要对其进行粘性修正．进行耦合的边界层和势流求解是一种常用的粘性修正方法,通过该方法可以包含边界层的影响,进而计算粘性阻力,但需要边界层和势流的耦合迭代求解,计算量大．

文中采用一种简单的方法进行粘性阻力修正．首先,确定位于水下滑翔机后缘的面元个数,并以每个后缘面元的中点为展向位置,截取水下滑翔机的横截面,建立等后缘面元个数的翼型剖面．

然后,假设在每个翼型剖面上,粘性阻力系数与升力系数是二次函数关系:

(7)

式中：cd0为每个翼型剖面的粘性阻力系数；cl为每个翼型剖面的升力系数；α1,α2,α3为二次函数系数，其与各个翼型剖面的局部雷诺数有关,具体通过各个翼型的阻力极曲线或者阻力数据拟合函数计算．

最后,在展向方向对每个翼型剖面的粘性阻力系数进行积分,即可得到整个水下滑翔机的粘性阻力系数,进而对升阻比进行粘性修正．

2.3 翼身融合水下滑翔机实例验证

采用一型左右对称的翼身融合水下滑翔机对提出的升阻比快速计算方法进行验证,其具体外形如图1．分别采用Fluent软件和所提方法计算不同攻角下的升阻比大小,并将结果进行对比．需说明的是因外形左右对称,使用Fluent软件和所提方法计算升阻比时,均设置对称边界,取右半边外形进行计算,以加快计算速度．图2为使用文中所提方法进行翼身融合水下滑翔机升阻比计算时的面元网格,图3为计算后的表面压力系数分布．

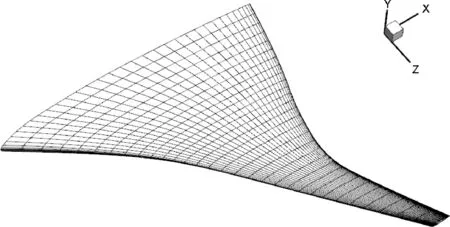
图2 翼身融合水下滑翔机表面的面元网格

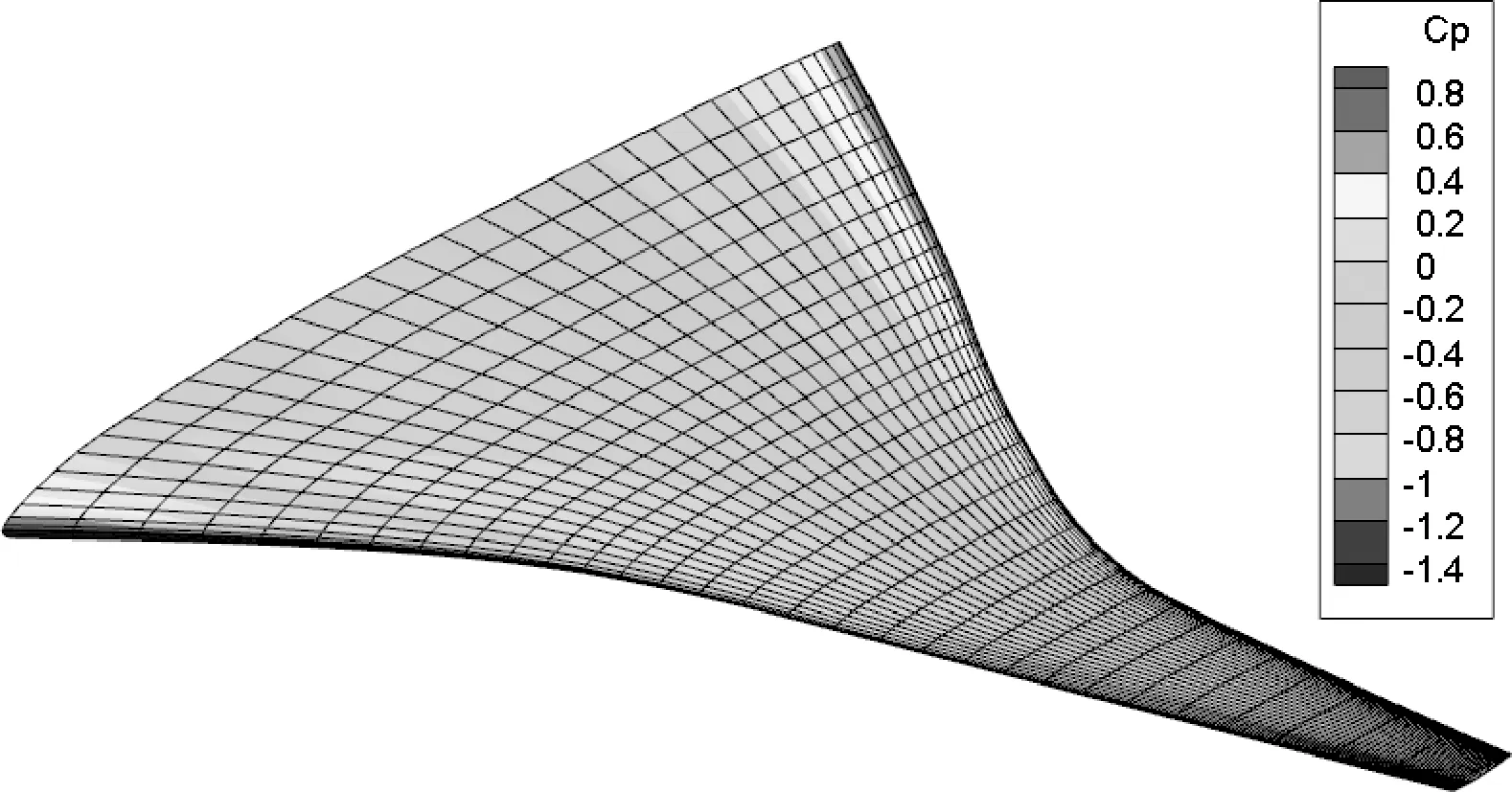
图3 翼身融合水下滑翔机表面的压力系数分布

表1为不同攻角下,Fluent软件和文中所提方法计算的升阻比大小．

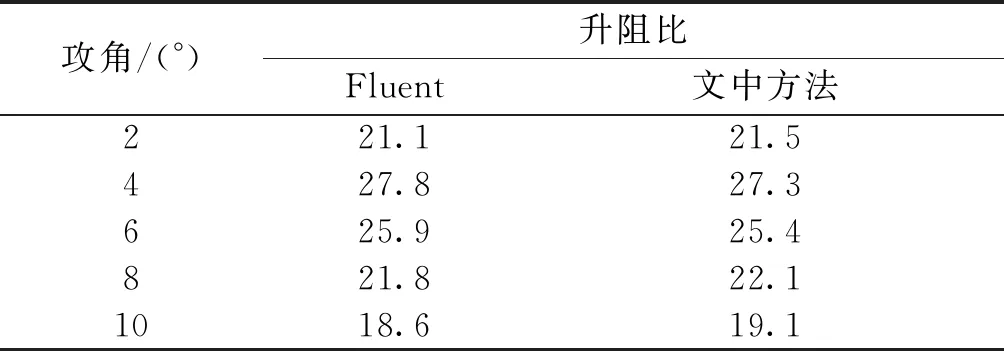
表1 Fluent和文中方法的升阻比计算结果对比

分析表1可知,与Fluent计算结果相比,文中所提方法的计算误差在3%以内,满足后续分析所需的计算精度要求．

3 外形参数对升阻比的影响

基于DOE方法进行翼身融合水下滑翔机外形参数的样本采样,并建立回归模型进行外形参数对升阻比的影响大小分析．

3.1 最优拉丁超立方采样

进行升阻比主因素分析前,需要采用DOE方法合理而有效地获得不同水下滑翔机外形参数相关联的升阻比数据值,并使用最少的样本点数目获得最多的升阻比信息．

目前,常用的DOE方法主要包括全因子设计、部分因子设计、正交数组、中心组合设计、拉丁超立方设计、最优拉丁超立方设计等[16]．其中,拉丁超立方设计对设计空间的填充能力强,相比全因子设计,可以用更少的样本点填充满整个空间.此外,拉丁超立方设计的拟合非线性响应能力强,相比正交试验,采用同样的样本点个数可以研究更多的因素组合．最优拉丁超立方设计是对拉丁超立方设计的进一步改进,使所有的样本点更加均匀地分布在整个设计空间,具有更好的空间填充性和均衡性．因此,文中使用最优拉丁超立方方法进行翼身融合水下滑翔机样本点的采样．

首先,选择翼身融合水下滑翔机的外形左右对称,取一半外形进行升阻比计算,文中仅选取与右半边6个翼型剖面相关联的参数作为试验设计的因子,且具体分为两类:① 6个翼型剖面的厚度比例参数Thicki(i=1,…,6),通过改变其值的大小可改变每个翼型剖面的厚度;② 6个翼型剖面的扭转角参数Thetai(i=1,…,6),通过改变其值大小可改变每个翼型剖面在xy平面的旋转角度．

此外,考虑到翼身融合水下滑翔机的攻角对升阻比的影响显著,文中还将攻角Alpha作为试验设计的因子．综上,各个试验因子的具体描述如表2．

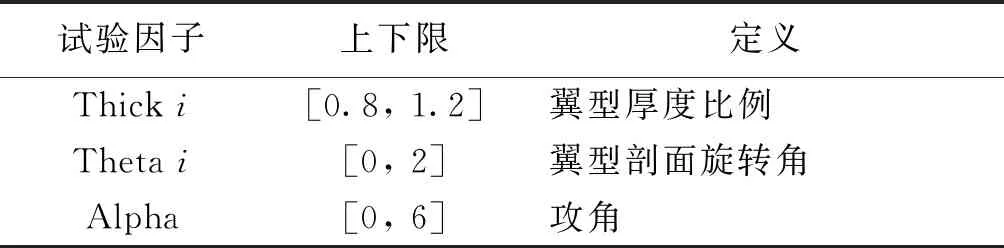
表2 试验设计因子描述

对于上述翼身融合水下滑翔机的13个试验设计因子,采用最优拉丁超立方方法对其进行取样,设置取样个数为50个.针对生成的50个参数样本点,采用文中提出的方法快速计算相应的水下滑翔机升阻比L/D数据值．

3.2 外形参数对升阻比的影响排列

使用多元二次回归模型[17]进行各种翼身融合水下滑翔机外形参数对升阻比的影响大小排列．

首先,根据以上得到的水下滑翔机参数样本点和升阻比L/D数据值,建立多元二次回归模型:

(8)

式中：θ、αi、βi和γij为回归模型中各项的系数．αi、βi和γij反映了回归模型中每一项对响应的效应.其中：αi为回归模型的线性主效应；βi为回归模型的二阶主效应；γij为回归模型的交互效应．

为了更客观、直观地反应各个输入变量对响应的影响,对多元二次回归模型的建立过程进行归一化．首先,将输入变量统一归一化到[-1,+1]后,使用最小二乘法求式(8)中系数;然后,将归一化后的回归模型系数通过式(9)转化为影响率百分比．

(9)

然后,基于由式(8、9)建立的归一化多元二次回归模型及计算出的影响率百分比,使用Pareto图描述回归模型中各项对升阻比的影响程度百分比(图4),图中浅色的条形表示正影响,深色的条形则表示反影响．

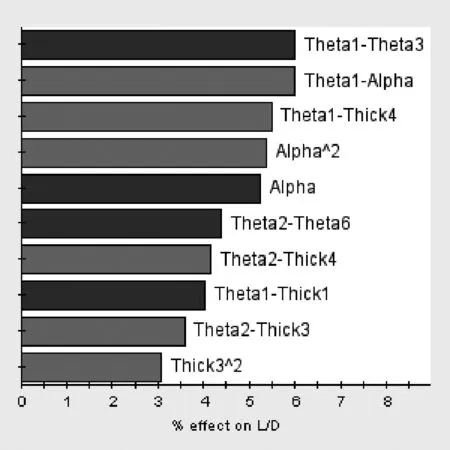
图4 各类参数对升阻比L/D影响的Pareto图

由图4可知,Theta 1和Theta 3的乘积项对L/D具有最大的正影响,Theta 1和Alpha的乘积项对L/D具有最大的反影响;紧接着对L/D具有正影响的因素从大到小依次为Alpha、Theta 2和Theta 6的乘积项、Theta 2和Thick 1的乘积项等,对L/D具有反影响的因素从大到小依次为Theata 1和Thick 4的乘积项、Alpha的平方项、Theta 2和Thick 4的乘积项等．综合来看,扭转角参数、攻角参数和两者的耦合项对L/D的影响显著,厚度比例参数及与其有关的耦合项对L/D的影响相对较弱,因此,在翼身融合水下滑翔机的外形设计过程中,应主要对扭转角参数和攻角参数进行调整,以改善翼身融合水下滑翔机的升阻比特性．

4 结论

(1) 提出一种翼身融合水下滑翔机的升阻比快速计算方法,该方法首先基于势流理论计算出压力分布和诱导阻力,再进行粘性修正,计算出精确的升阻比．相比于CFD方法,所提方法计算耗时少,仅需生成表面网格,对网格的质量要求低.实例验证表明，所提方法的计算误差在3%以内．

(2) 基于提出的升阻比快速计算方法,对最优拉丁超立方设计生成的样本点进行自动升阻比计算,并建立多元二次回归模型对计算的数据进行分析.结果表明，扭转角、攻角和其耦合参数对L/D的影响显著,在翼身融合水下滑翔机外形设计中应优先调整以提高设计效率．