飞行器径向连接螺栓振动断裂分析
瞿绍奇,孙英超,邬亨贵,李延平,张伟
航空工业洪都,南昌 330024
飞行器结构在使用服役期间,往往由于经受振动环境造成飞行器结构在一些关键部位发生破坏,导致飞行器结构或功能失效[1-2]。当前,结构振动疲劳受到国内学者和工程师的重视[3-6],针对具体工程问题开展了深入研究[7],获得了很多具有工程指导意义的成果[8-15]。
振动环境下结构应力响应分析有时域和频域2种分析方法。时域分析方法存在获取典型载荷-时间历程较困难,以及结构应力响应处理计算量巨大等问题,在工程结构中应用较少。基于功率谱密度的频域分析方法因计算简单、不需要循环计数的优点,广泛用于结构随机振动疲劳寿命分析[16-17]。
本文针对某飞行器套接径向螺栓在振动试验中发生断裂,应用频域分析方法对其进行振动疲劳寿命估算。由于频率分析方法无法适用于存在边界非线性结构,然而,径向连接螺栓在传力特性上和本体之间固然存在接触非线性关系;工程上对该类问题的研究偏少[18-19]。为克服该困难,论文尝试对线性模型进行有限元频响分析获得螺栓的载荷功率谱密度(Power Spectrum Density,PSD);通过螺栓剪力与螺栓头根部弯曲应力的工程计算关系,建立载荷与应力的参数化转换关系,获得螺栓断裂部位的名义应力功率谱密度,并采用Dirlik经验公式[20],联合Miner线性累积损伤模型和经应力集中系数修正的材料S-N曲线,对飞行器径向连接螺栓振动疲劳寿命进行估算。
1 基于功率谱密度的疲劳寿命估算公式
根据疲劳寿命统计规律,疲劳寿命曲线幂指数表达式为
smN=c
(1)
式中:c、m为材料常数;N为应力峰值为s时的破坏循环次数。
根据Miner线性累计损伤理论,多级应力下结构的累积损伤为
(2)
式中:ni为第i级载荷时的实际循环频次;Ni为第i级载荷时的破坏循环数;k为疲劳载荷谱包含的载荷总数。
当循环应力连续变化时,式(2)可转化为
(3)
式中:n(s)为应力峰值为s时的实际循环频次;N(s)为应力峰值为s时的破坏循环数。
文献[20]所述Dirlik经验估算方法,基于应力功率谱密度,给出了n(s)数学表达式
n(s)=E[p]Tp(s)
(4)
式中:T为时间;p(s)为应力随机过程的峰值概率密度函数;E[p]为预期波峰数。
p(s)={(D1/Q)exp(-z/Q)+(D2z/R2)·
(5)
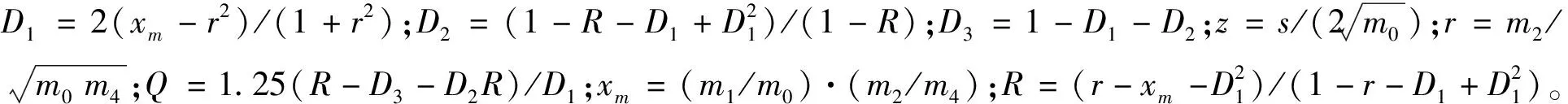
(6)
功率谱密度第n阶惯性矩为
(7)
式中:f为积分频率;G(f)为功率谱密度。
将式(1)、式(4)代入式(3),且令D=1,获得结构的疲劳寿命估算公式
(8)
2 飞行器螺栓振动疲劳寿命分析
某飞行器在振动试验中,舱段连接处径向连接螺栓在螺栓头根部发生断裂,结构简图及断裂螺栓位置如图1所示,螺栓规格为M5的120°沉头螺栓。针对断裂事故,采用基于功率谱密度的疲劳寿命估算方法进行分析。
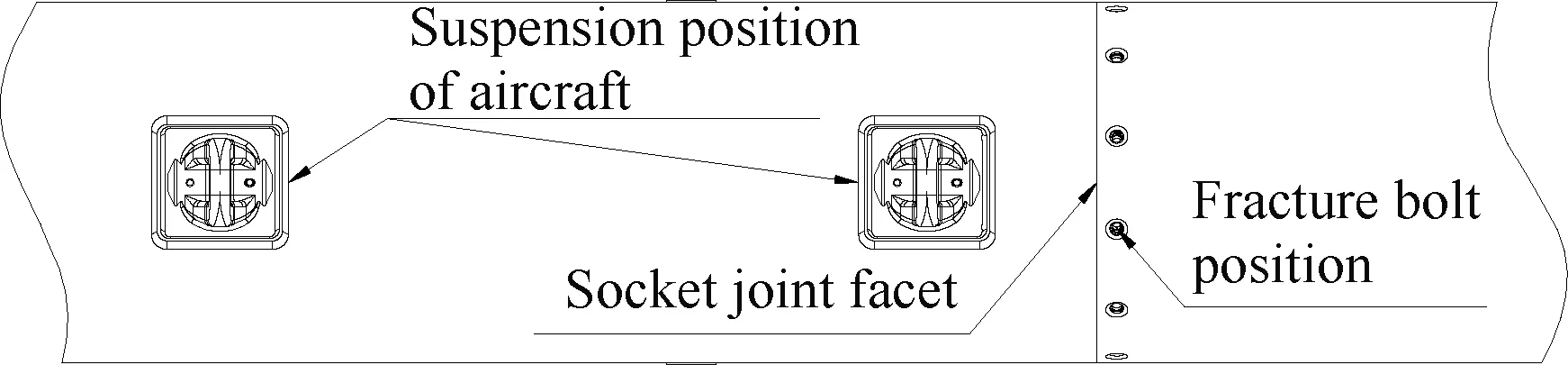
图1 某飞行器舱段结构简图
2.1 获取螺栓载荷功率谱密度
建立飞行器结构有限元模型,采用弹簧单元模拟螺栓连接,对其进行模态分析,并与试验结果进行了比较,见表1。

表1 有限元计算模态与试验模态对比
在图1所示悬挂处模拟试验环境施加约束,根据模态试验结果选取结构阻尼为0.026,利用有限元工具获取单位基础激励传递函数。按振动试验在20~2 000 Hz频率范围内,施加沿飞行器法向0.02g2/Hz随机激励,获取舱段断裂螺栓处法向Y和轴向X加速度功率谱密度,见图2和图3,RMS(Root Mean Square)为均方根值。
对比图2和图3飞行器断裂螺栓处法向和轴向加速度功率谱,施加飞行器法向激励时,轴向加速度功率谱密度最大的2个共振峰分别出现在飞行器法向一弯和二弯模态处,符合梁弯曲模型的轴向力学特性。

图2 断裂螺栓有限元法向加速度功率谱密度(RMS: 4.38g)

图3 断裂螺栓有限元轴向加速度功率谱密度(RMS: 0.44g)
振动试验飞行器断裂螺栓处法向加速度功率谱密度见图4。考虑轴向加速度功率谱与法向加速度功率谱的相关性,将有限元分析获得舱段断裂螺栓处法向加速度功率谱在飞行器法向一弯和法向二弯模态处的峰值及RMS值与图4试验数据进行对比,见表2。

表2 有限元计算功率谱与试验对比

图4 断裂螺栓试验法向加速度功率谱密度(RMS: 4.80g)
有限元分析获得飞行器断裂螺栓处沿飞行器
轴向剪力Fx功率谱密度见图5。对比图3轴向加速度功率谱和图5轴向剪力功率谱,二者功率谱密度最大的2个共振峰均出现在飞行器法向一弯和二弯模态处。剪力在法向一弯模态处的功率谱密度为3.15×104N2/Hz,在法向二弯处为0.18×104N2/Hz,一弯模态处能量密度为二弯的17.5倍,表明一阶弯曲模态引起的共振为造成螺栓破坏的主要因素。

图5 断裂螺栓载荷功率谱密度(RMS:661.8 N)
2.2 建立径向连接螺栓载荷-应力转换关系
套接螺栓断裂部位受力状态如图6所示,Fy为螺栓头附加拉力;Fn为螺栓头锥面法向载荷。考虑在图5中螺栓剪切载荷功率谱作用下,在螺栓头根部产生的弯曲应力[21],建立断裂部位载荷-应力关系。
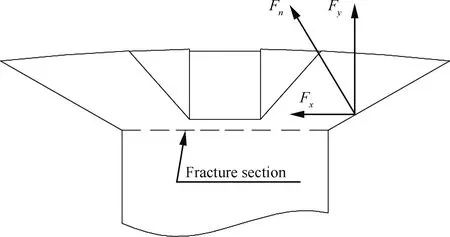
图6 螺栓断裂部位受力状态
螺栓头根部截面弯矩为
M=Fy·d/2=Fx·tanθ·d/2
(9)
式中:d为螺栓直径;θ为螺栓沉头角。
螺栓头根部弯曲极值应力为
(10)
根据式(10),定义螺栓剪切载荷-弯曲应力转换系数为
(11)
根据建立的载荷与应力的转换关系,当螺栓直径d=5 mm、螺栓沉头角θ=120°时,确定螺栓头根部载荷-应力转换系数为σcf=0.353;据此,获取螺栓断裂部位的名义应力功率谱密度,见图7。

图7 螺栓头根部名义应力功率谱密度(RMS:233.6 MPa)
2.3 螺栓随机振动疲劳寿命估算
根据式(5)计算获取螺栓头根部应力随机过程的峰值概率密度函数,过程数据见表3,概率密度函数曲线见图8。根据式(6),获得预期波峰数E[p]=120。
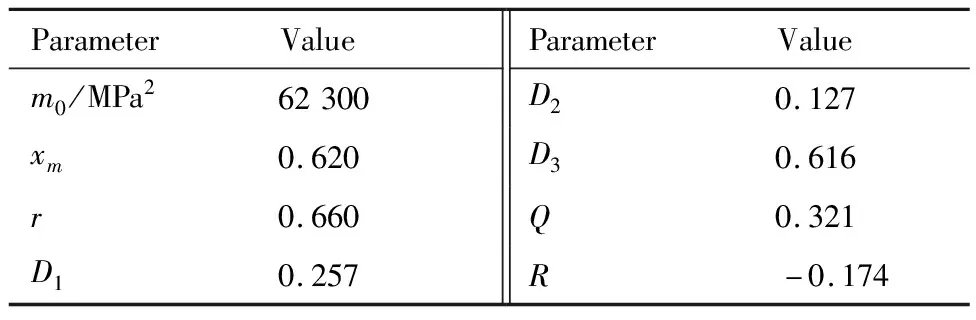
表3 峰值概率密度函数计算过程数据
螺栓材料为30CrMnSiA,根据文献[22]所给数据,获得材料的S-N曲线数据,结合式(1)进行计算,获得材料参数m、c值,见表4,各级应力损伤见图9。

表4 螺栓头根部S-N曲线及相关参数

图9 各级应力损伤
对峰值概率密度函数p(s)进行概率累积计算,获得中值寿命对应的应力值为σ0.5=362 MPa。
将各参数代入式(8),通过分段积分计算获得螺栓头根部中值寿命为39.5 min。振动试验持续40 min后,发现螺栓头断裂脱落;对螺栓头断口处进行金相分析,鉴定螺栓破坏形式为疲劳断裂。因此,分析结果与试验螺栓断裂现象符合。
3 结 论
1)针对某飞行器径向连接螺栓在历经40 min 振动试验后发生疲劳断裂,本文提出的方法计算获得螺栓头根部的中值疲劳寿命为39.5 min,符合试验现象。
2)试验和理论分析均显示断裂螺栓在飞行器一阶和二阶弯曲模态处产生了共振,但理论分析发现一阶共振频率处螺栓剪力功率谱密度为二阶共振频率的17.5倍,表明螺栓断裂的原因为低频共振疲劳。

