基于应变测量的结构载荷分布反演方法

兑红娜,刘栋梁,张志贤,潘绍振,杨龙

中国航空工业集团公司成都飞机设计研究所 强度部,成都 610091

结构健康监控是新一代航空航天器一项重要且具有挑战性的技术[1],其中需解决的关键问题是准确地测量与监控结构在飞行中所承受的载荷分布、应力场等信息[2]。在结构表面布置载荷传感器来直接测量载荷分布是不现实的,常用的方法是采用应变测量对载荷进行反演[3-8](也称反推),这显然是一个根据结构响应推测结构载荷输入的反问题。

反问题很有挑战性,因为它往往是病态(也称不适定)的,即应变测量的小误差会导致载荷反演的较大偏差。此外,不同的载荷输入可能导致相似的应变响应,因此反问题的解可能不是唯一的。

相比传统的基于应变电桥的部件载荷标定(如机翼根部弯矩/剪力/扭矩),本文研究的载荷分布反演需在结构全局更多的位置测量应变,以获取整个结构足够广泛且稳定可靠的应变分布。相比电阻式应变片,光纤传感器具有重量轻、测量范围广、寿命长、抗电磁干扰及抗恶劣环境的优势,可为载荷分布反演提供有利的条件。

国内外学者已经提出多种基于应变测量反演静态载荷的方法,其中,应用最广泛的是影响系数法[4-8]。文献[4-8]中大部分算例是基于有限元分析进行理论验证,少量的试验验证也仅是简单悬臂梁,目前未见有大型复杂传载结构(如真实飞机机翼)的应用实例。

影响系数法基于线弹性假设,认为由不同载荷工况下结构响应分布(如位移场、应力场、应变场等)的线性组合可以映射到结构载荷分布的线性组合。

1 影响系数法

影响系数法构建如下线性矩阵方程：

εg×1=Αg×mβm×1

(1)

fn×1=Pn×mβm×1

(2)

式中：εg×1表示未知载荷工况下的应变分布;fn×1表示未知载荷工况下的载荷分布;Ag×m表示影响系数矩阵;Pn×m表示单位载荷矩阵;βm×1表示线性系数;g表示应变测点数量;m表示单位载荷工况数量;n表示载荷加载点数量。

影响系数矩阵A通过施加单位载荷工况P来确定,影响系数可以是物理试验的实际测量值,或者有限元分析值。其中,单位载荷可以是单点载荷或载荷基函数,详见下文介绍。

注意,式(1)和式(2)并非文献[4]中的原式,本文作者进行了重组和归并,以便更清晰地表达影响系数法的内涵。

根据单位载荷的类型,影响系数法又分为单点载荷法和载荷基函数法。

1.1 单点载荷法

在单点载荷法中,单位载荷工况是仅对某个载荷加载点施加单位载荷,此时,m=n,P为单位矩阵,P=diag(1,1,…,1)。

式(1)和式(2)可以合并为

εg×1=Αg×mfm×1

(3)

式中：影响系数aij表示由于在加载点j处施加单位载荷引起的位置i处的应变,i=1,2,…,g,j=1,2,…,m。

在复杂结构的地面试验中,考虑到集中载荷对局部加载区域的影响,每个加载点的载荷最大值是有限制的,因此在单位点载荷下大部分区域的应变响应并不大,这会对载荷反演精度造成不利的影响。因此,对于复杂结构,单点载荷法不适用于地面试验验证。

1.2 载荷基函数法

在载荷基函数法中,假设载荷分布满足某种函数形式,单位载荷工况是施加某种载荷基函数形式的单位载荷分布,用fj表示。通常,m≠n,P=[f1,f2,…,fm]。

影响系数aij表示由于施加第j个载荷基函数{fj}的载荷分布引起的位置i处的应变,i=1,2,…,g,j=1,2,…,m。

文献[5]将基函数fj取为沿翼面展向和弦向的多项式分布函数,如常数、线性、二次、指数及正弦函数等。

文献[6]将基函数fj取为沿翼面展向和弦向的傅立叶级数项,如常数、单傅立叶项、双傅立叶项等。

载荷基函数法的难点在于如何选取合适形式和数量的载荷基函数。在实际试验中,作动筒加载点是有限的,且同一个作动筒和杠杆系统的载荷分配比例是固定的,很难模拟出复杂的载荷基函数。因此,对于复杂结构,载荷基函数法同样不适用于地面试验验证。

1.3 讨 论

经分析,载荷分布反演精度主要取决于以下几方面：

1)单位载荷工况的选取(决定P)

对于单点载荷法,直接对各加载点施加单位载荷工况即可。对于载荷基函数法,载荷基函数的类型和数量直接影响载荷空间的完备性,如果选取的不合适,将很难准确预测任意载荷工况下的载荷分布。

2)应变测点数量和位置的选取(决定A)

应变测点应尽量分散,且对加载点载荷的敏感度较高,若某些加载点的载荷变化不能体现在应变测量值上,则该加载点是很难被准确预测的。

3)反向矩阵病态化的减弱(决定β)

在实际应用中,应变分布不可避免地存在测量误差,需引入有效正则化方法来求解线性矩阵方程(式(1)),以降低病态化对载荷反演鲁棒性的不利影响。

本文重点针对以上1)和3)展开研究。

2 基工况筛选法

为解决单位载荷工况选取的难题,本文提出一种基于施密特正交化的最大垂直距离逐步筛选基工况法(下文简称为基工况筛选法),总体思路是依次挑选出与当前欧式空间垂直距离最大的工况(或向量)组成新的欧式空间,直至所有工况(或向量)均位于该欧式空间,挑选出的工况即为基工况,详细步骤见2.1节。

相比单点载荷法和载荷基函数法,基工况筛选法从设计载荷工况库中筛选基工况,单位载荷工况是更为真实的载荷分布,便于在结构地面试验中施加。

基于基工况筛选法的载荷分布反演流程见图1,重点在于首先从载荷空间筛选出载荷基工况,然后在应变基工况包含载荷基工况的前提下,进一步从应变空间筛选出应变基工况,详细步骤见2.2节。图1中候选应变集指的是结构上根据实际情况可允许布置的应变测点集。

图1 基于基工况筛选法的载荷分布反演流程

2.1 载荷基工况

将设计载荷工况的载荷分布矩阵表示为Pn×M=[f1,f2,…,fM],每个列向量fi表示一个载荷工况,M为设计载荷工况数量,n为载荷分布的加载点数量。

载荷列空间属于n维欧式空间的子空间,只要确定一组线性无关的基向量,即基工况,则任意载荷工况均可用这组基工况来线性表示,此空间记为En×mf,mf为基工况数量。

基于施密特正交化法,从设计载荷工况库逐步筛选出载荷基工况,具体步骤[9]为

步骤2选取某个载荷工况作为初始基工况,记为f1,将其单位矢量记为e1,得到一维载荷列空间En×mf,mf=1。

(4)

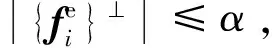
从以上步骤可知,载荷列空间的基工况组合不是唯一的,初始基工况f1和误差阈值α决定了最终的基工况组合。在实际应用中,可将重要考核工况(如载荷最大工况)选为初始基工况。经研究分析,误差阈值α取为所有设计载荷工况单位化后最小标准偏差的1/10～1/15较为合理。

通常,载荷向量的维数n越大,构建完备载荷列空间所需的基工况m就越多。在结构有限元分析中,气动载荷和惯性载荷节点通常很密,但在实际地面试验时,可用独立的作动筒载荷表示载荷分布。

2.2 应变基工况

将设计载荷工况的应变分布矩阵表示为Ag×M=[ε1,ε2,…,εM],每个列向量εi表示一个载荷工况,M为设计载荷工况数量,g为应变测点数量。

在载荷基工况的基础上,进一步从设计载荷工况库筛选出应变基工况。将第2.1节的载荷分布矩阵Pn×M替换为应变分布矩阵Ag×M,并对筛选步骤2作如下修改：

步骤2选取已筛选出的mf个载荷基工况作为初始应变基工况组合,根据施密特正交化公式,将其转换为标准正交矢量,得到mf维应变列空间Eg×mf。

其他步骤保持不变,可依次筛选出mε个应变基工况,mε≥mf,mε≤M,mε≤g。此时,确定了影响系数矩阵Ag×mε和基载荷矩阵Pn×mε。

在以上步骤中,步骤2是关键,应变基工况包含载荷基工况的准则确保了载荷分布反演精度。

3 正则化方法

常规最小二乘法无法解决反向矩阵病态化的问题,需引入合适的正则化方法来求解线性矩阵方程,从而提高载荷分布反演的鲁棒性。

在众多正则化方法中,应用最广泛的是Tikhonov正则化法[10]。与常规最小二乘法不同,正则化法的关键是增加特定的正则项来加权误差平方和极小的条件,以克服不适定性,使解唯一且稳定。

对于式(1)的线性矩阵方程,Tikhonov正则化的准则为

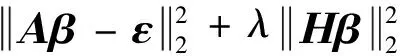
(5)

式中：H为正则化矩阵；λ为正则化参数。在众多正则化参数优选方法[10]中,最常用的是L-曲线法和广义交叉验证法,哪种方法更优需根据具体情况而定。

由于篇幅有限,关于Tikhonov正则化的具体算法,本文将不再赘述,详见文献[10-11]。

4 算 例

基于某型飞机机翼疲劳试验的作动筒载荷和光纤传感器数据,对本文提出的基于基工况筛选法的载荷分布反演方法(见图1)进行试验验证。本节所有图例中的载荷均经过无量纲化处理。

机翼疲劳试验共749种独立载荷工况(M=749),左机翼下翼面共布置24个加载作动筒(n=24),4根主梁沿翼展方向均粘贴光纤传感器,有效应变测点共116个(剔除损坏/异常测点),在本算例中将其作为候选应变集(g=116)。为消除应变测量误差的影响,对每个候选应变测点取同工况多次测量值的均值,组成候选应变矩阵A116×749。

首先,根据作动筒载荷矩阵P24×749,采用2.1节所述方法,以最大机翼弯矩工况作为初始工况,阈值取为所有载荷向量单位化后最小标准偏差的1/10,逐步筛选出23个载荷基工况,mf=23。基工况下的载荷分布情况见图2。

图2 基工况载荷分布

然后,根据候选应变矩阵A116×749,采用2.2节所述方法,基于已筛选出的23个载荷基工况,逐步筛选出82个应变基工况,mε=82,此时确定了影响系数矩阵A116×82和基载荷矩阵P24×82。

假设749种试验工况下的载荷是未知的,仅已知各工况下的应变分布εi,应变测量误差按以下3种情况：无误差、5%随机误差和10%随机误差,根据式(1)和式(2),分别采用常规最小二乘法和Tikhonov正则化法预测749种工况的作动筒载荷,并根据作动筒位置进一步计算子部件总体载荷(机翼根部剪力/弯矩/扭矩、舵面剪力/铰链力矩),将载荷预测值与实际值进行对比,以验证以上载荷分布反演方法的预测精度和鲁棒性。

4.1 无测量误差

假设未知工况下的应变测量值无误差,采用以上步骤进行载荷分布反演,见图3,绘制了采用常规最小二乘法的24个作动筒载荷对比图,横坐标为载荷实际值,纵坐标为载荷预测值,图中每个数据点代表一个载荷工况。可见：除4#、5#、15#、16#、20#作动筒稍差外,大部分作动筒的载荷预测精度很高。其中,4#、5#靠近机翼根部,15#、16#位于副翼,20#位于前襟。

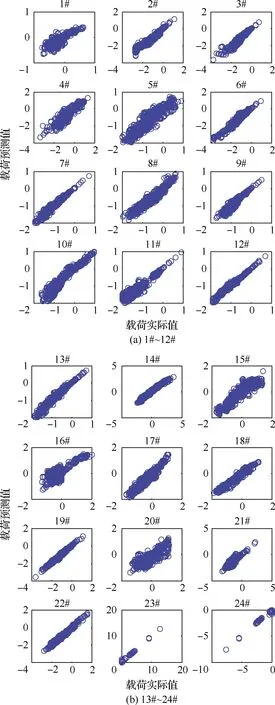
图3 作动筒载荷预测值与实际值对比(最小二乘法)

舵面作动筒(15#、16#、20#)预测精度稍差是符合预期的,因为光纤传感器仅布置在几根主梁的缘条上,这些应变测点对舵面载荷的响应并不大。若重点关注舵面载荷,则应增加舵面区域的应变测点,舵面载荷的预测精度自然会提高。

4#、5#作动筒预测精度差是由于存在多种载荷分布导致相似应变响应的情况,见图4,第2个和第7个基工况的载荷分布明显不同,但应变分布却很接近。这种情况是不可避免的,虽然不能保证单独加载点的预测精度,但部件总体载荷(如机翼根部剪力/弯矩/扭矩)以及总体应变分布是能准确反映的。

图4 不同载荷分布下的相似应变响应

子部件总体载荷对比图见图5,横坐标是载荷实际值,纵坐标是载荷预测值,图中每个数据点代表一个载荷工况。可见：虽然部分作动筒的载荷预测精度有限,但部件总体载荷的预测精度很高。

图5 子部件载荷预测值与实际值对比(最小二乘法)

由于本算例的应变空间(g=116)是充分的,正则化方法的精度提升效果并不明显,这里仅列出最小二乘法的结果。

4.2 随机测量误差

对未知工况下的应变测量值分别引入5%和10%的随机误差,采用以上步骤预测749工况的作动筒载荷和子部件载荷,并采用广义交叉验证法来确定Tikhonov正则化参数。

由于篇幅有限,此处仅绘制部件总体载荷对比图,如图6和图7,横坐标为载荷实际值,纵坐标为载荷预测值,图中每个数据点代表一个载荷工况。可知：

图6 引入5%随机测量误差的子部件载荷预测值与实际值对比

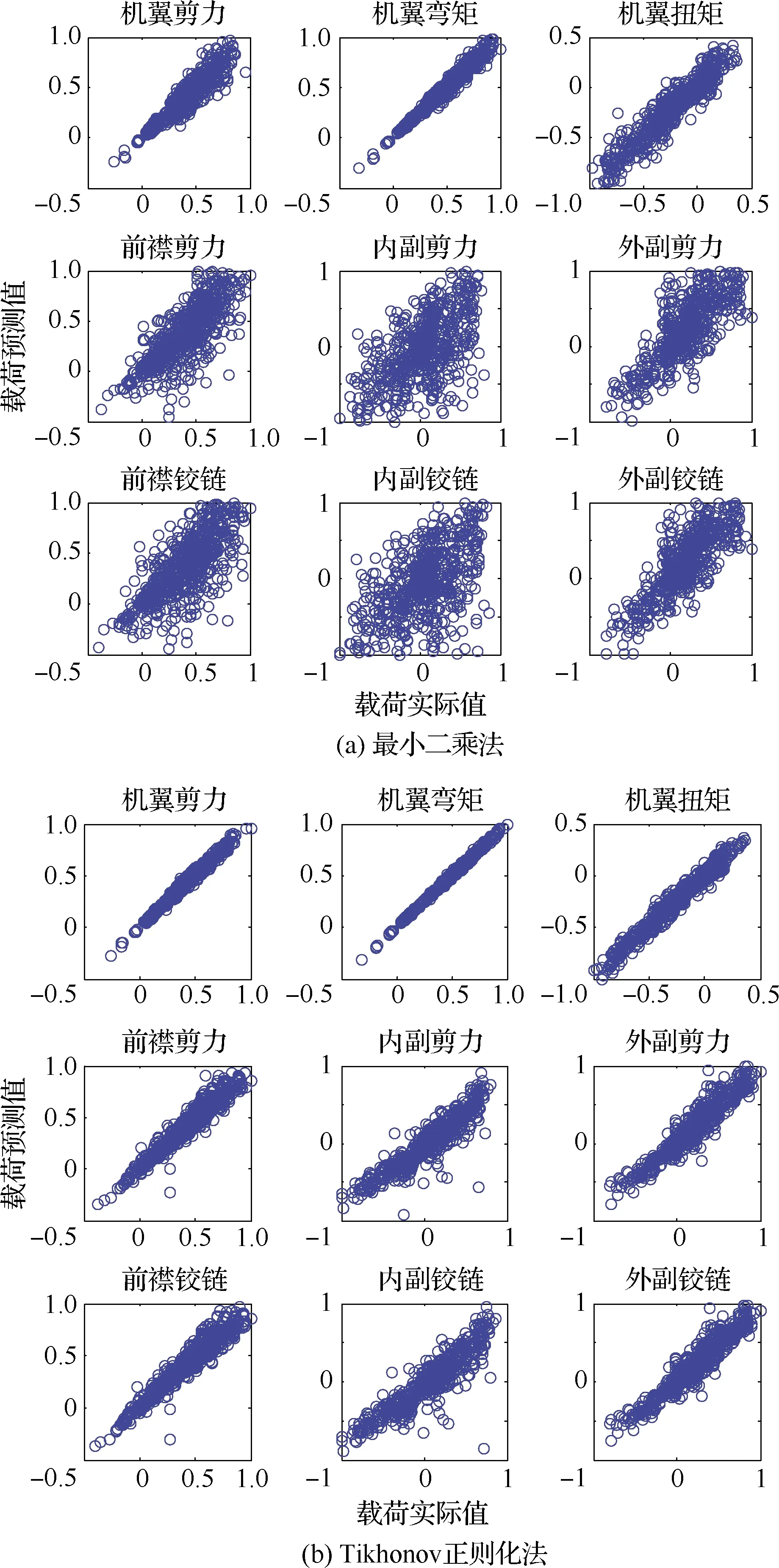
图7 引入10%随机测量误差的子部件载荷预测值与实际值对比

1)对于常规最小二乘法，随着应变测量误差的增大，载荷反演精度迅速变差，当随机误差为10%时，精度已差到无法接受。

2)对于Tikhonov正则化法，随着应变测量误差的增大，载荷反演精度的降低是缓慢的，说明正则化方法可有效减弱病态化对载荷反演精度和鲁棒性的不利影响。

5 结 论

本文针对基于应变测量的载荷分布反演,提出了一种基于施密特正交化的最大垂直距离逐步筛选基工况法,从设计载荷工况库中筛选载荷基工况和应变基工况,建立了一套完整的工程可行的载荷分布反演流程,具体总结如下：

1)相比单点载荷法和载荷基函数法,本文提出的基工况筛选法从设计载荷工况库中挑选出线性无关的基工况,单位载荷工况是更为真实的载荷分布,便于在结构地面试验中施加。

2)本文提出应变基工况应包含载荷基工况的准则,以确保载荷分布反演精度。

3)经验证,Tikhonov正则化法可有效减弱反向矩阵的病态化,大大提高载荷反演精度和鲁棒性。

4)经验证,本文提出的载荷分布反演方法是工程可行的,且具有很高的预测精度和鲁棒性,可为新一代航空航天器的结构健康监控提供一条可靠的载荷识别途径。