勾股定理的逆定理的应用举例
摘要:本文探讨了勾股定理的逆定理的应用举例,通过实例说明勾股定理的逆定理可以有很好的实际应用,介绍勾股定理的逆定理的结构特点,分析了勾股定理的逆定理的几何意义,研究了勾股定理的逆定理在解决相关实际问题的可行性,在此基础上,说明勾股定理的逆定理的应用的必然性。
关键词:勾股定理的逆定理;应用例子; 数形结合;
一、引言
1.培养学生认识勾股定理的逆定理应用的社会历史背景
在中国,相传4000多年前,大禹曾在治理洪水的过程中,利用勾股定理来测量两地的地势差,在3000多年以前,中国人已经知道用边长为3,4,5的直角三角形来进行测量。
勾股定理是初等几何中的一个基本定理,是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,所以它的逆定理也是初中数学中最重要的几个定理之一,它提出了直角三角形的三条边的数量关系是以后学习直角三角形的重要依据之一,它可以帮助我们了解很多与线段求值有关的问题,在现实世界中有着广泛的应用,且对其他学科也有重要意义。直角三角形的判定方法体现了数学中的重要思想——数形结合思想。
2.培养学生对勾股定理的逆定理應用的目的、意义
在讲解勾股定理的逆定理的学习过程中,通过教学模型或多媒体动画演示,让学生直观地感受问题情境,并自觉地进行数学思考,引导学生从实际问题中发现数学,体会数学的应用,激发学生学习的兴趣。通过学生的计算、画图、度量等活动,用自己的语言来归纳出相关的结论,并通过举例加深对勾股定理的逆定理的理解。在教学中,力争培养学生的“数学思考”能力,让学生从数学的角度思考问题,从“求异”的方向去思考问题。勾股定理的逆定理的应用课,着重以学生尝试解决问题为目的,侧重在学生尝试解题后进行讲评,在教师的点拨与分析的基础上,师生共同寻找解题的思路,在教学中,注重学生之间的交流、反思,让学生在交流中受益,在反思中提高。在活动中使学生明晰,生活中有很多问题都可以转化为直角三角形(对不规则图形进行“割”、“补”等方法),勾股定理的逆定理不仅在数学中,而且在其他自然学科中也被广泛应用,如解决圆柱侧面两点间的距离问题、航海问题、折叠问题、梯子下滑问题等,常直接或间接运用勾股定理的逆定理解决问题。在解决实际问题时,常先画出图形,根据已知条件计算出各边长,再利用勾股定理的逆定理判断三角形是否为直角三角形,最后解答问题。 二、对于勾股定理的逆定理应用的分析和应用
1.勾股定理的逆定理的命题初步认识
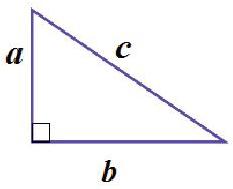
勾股定理的逆定理 :如果一个三角形的三条边长分别是a,b,c,满足,那么这个三角形是直角三角形。对于命题的理解,先要理解它的结构特点,题设(三角形的三边的数量关系:较短的两条边长的平方和等于最长边的平方)和结论(这个三角形的形状是直角三角形),达到学生对勾股定理的逆定理的初步理解的效果。
曾有一位学生刚学习了“勾股定理的逆定理”后,就跑到办公室来问我,“老师,如何找一个直角来使用”。我笑着对他说:“你有三角板吗?”他说:“没有。”“或者你有量角器吗?”“也没有。”“那么你应该有一张纸吧,用折纸的方法可以折出一个直角来。”“也没有。不过我手上刚好有3根木棒,一根3cm,一根4cm,和一根5cm,我用这3根木棒,首尾顺次相接成一个三角形,根据我们所学的数学知识,这个三角形是直角三角形,三个角中,其中一个角必定是直角。老师你认为有道理吗?它有什么理论依据?”。这位学生饶有兴趣地向我请教,我就详细地跟他讲解。勾股定理的逆定理:如果三角形的三条边长分别是a,b,c,满足,那么这个三角形是直角三角形。因为,所以能拼成一个直角三角形,找出一个直角来。你做得很好,能发现数学知识就在自己的身边,身边有很多的数学知识,只要你自己能细心思考,一定有很多办法去做每一件事。这个勾股定理的逆定理对于我们的日常生活有着积极的应用。
2.勾股定理的逆定理来源于生活,应用于生活。
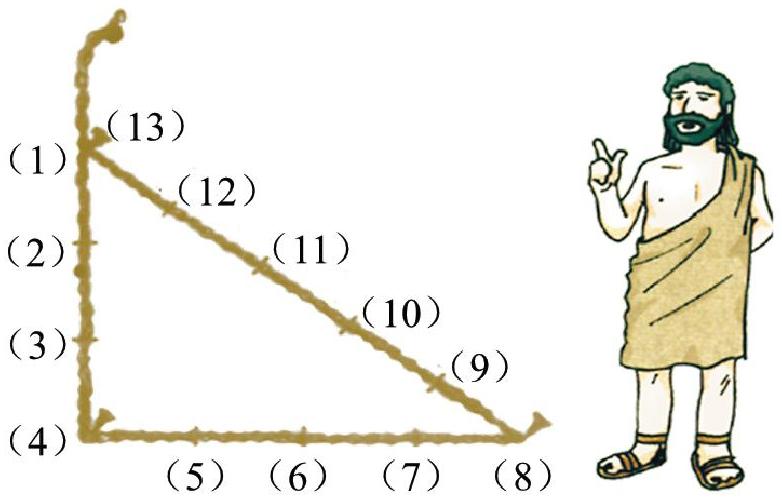
其实勾股定理的逆定理在我们实际生活中经常用到的。据说,古埃及人用一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。根据这个定理,(1)可以用来判定一个三角形的形状是否为直角三角形的理论依据。(2)三条线段能否围成一个直角三角形。(3)在没有量角器和三角板的情况下,制造出一个直角来(例如3、4、5(勾股数),这样的长度也能连接出一个直角三角形来)。
3.引导寻找勾股定理的逆定理的应用。
勾股定理的逆定理的学习,充分运用了“数形”结合的数学思想,“分割与组合”。
结语:
以上实际问题用勾股定理的逆定理来解决,我们可以知道,勾股定理的逆定理的地位与作用,用来计算、证明。当我们在野外探险时都可能用到勾股定理的逆定理,寻找一个直角来,解决实际需要。
当然可用的数学方法不止这一个“勾股定理的逆定理”,只要我们平时努力学习数学知识,细心观察,仔细思考,一定能找到解决的办法。“勾三股四弦五”,数学就在我们的身边。勾股定理的逆定理的未来的应用是非常广泛的。需要直角,创造直角,验证直角,还是我们的勾股定理的逆定理实用的必然性。
广东省新兴县稔村镇初级中学 黎达秋

