基于动态聚类的有限状态机多错误诊断
崔 玲, 张建标,3
(1.北京工业大学信息学部,北京 100124;2.可信计算北京市重点实验室,北京 100124;3.信息安全等级保护关键技术国家工程实验室,北京 100124)
近年来,基于人工智能的错误诊断成为研究热点. Li等[1]提出基于深度学习的齿轮故障诊断方法;Shi等[2]提出基于数据挖掘的航空电子系统故障诊断方法;文成林等[3]对基于深度学习的故障诊断方法进行了综述. 但是,目前研究多是基于单个错误的假设. 有关多错误诊断的研究多集中在软件错误定位方面,如基于数据挖掘的多错误定位[4-5]、基于程序切片的多错误定位[6]、基于聚类分析的多错误定位[7]等.
与软件的错误定位方法不同,对于基于有限状态机(finite state machine,FSM)的错误诊断研究不仅是定位错误,而且要找出错误原因并进行修正. 诊断的主要思想是枚举所有可能的错误,然后根据相关信息排除一些候选错误,从而生成错误诊断集. 由于枚举数量过于庞大,基于FSM的错误诊断也多是针对单错误的方法,而且研究多是针对具体系统[8-9]. Lee等[10]和Ghedamsi等[11]提出了基于FSM单个错误的通用诊断方法,而基于FSM的多个错误的诊断问题还没有有效可行的通用方法.
本文将聚类分析方法应用到基于FSM的错误诊断中,提出基于动态聚类分析的多错误诊断方法,将失败用例分类成簇,以期每簇只存在一个错误,进而实现多错误诊断.
1 基础术语

定义1转换错误
定义2输出错误
假设已有测试序列集C={c1,c2,…,cn},其中每个cm都是一个测试序列,对应输入序列im={im1,im2,…,imp},预期输出序列om={om1,om2,…,omp},实际输出序列o′m={o′m1,o′m2,…,o′mp}.通常,若某个测试序列的实际输出与预期输出不相符,则称之为失败用例,简称反例;反之简称证例.
定义3初始症状[12]
若在oi和o′i中有oij≠o′ij且对任意1≤k≤j有oik=o′ik,则称oij≠o′ij为初始症状,记为e0.
定义4冲突集[11]
在某个症状e之前测试序列所经过的转换称为该症状的冲突集(conflict set),记为SC(e).
定义5冲突序列
称某个症状e的冲突集对应的测试输入序列段为冲突序列(conflict sequence).
2 多错误诊断方法
基于聚类分析的软件多错误定位方法主要分为3个步骤:首先,根据聚类算法将程序失败用例进行聚类;然后,使用Tarantula方法[13]计算每条语句发生错误的可疑度;最后,按照可疑度降序排名人工检查程序代码,从而完成程序错误定位.
本文提出的诊断方法中聚类方法为动态聚类,首先进行初始分类,在分析过程中进行再次聚类.
由定义可知,初始症状冲突集中必定至少包含一个错误,而FSM的执行轨迹总是从初始状态开始,那么具有相同的初始症状冲突集的反例发生的错误必定相同. 因此,初始分类时可将具有相同的初始症状冲突集的反例聚类. 其次,一个错误转换可能出现在不同的初始症状冲突集中,在分析该转换时,将所有初始症状冲突集包含该转换的反例聚类,然后进行错误诊断.
2.1 可疑度计算
多错误诊断复杂的地方在于,如果错误类别是转换错误,那么错误是具有传递性的,也就是说,初始症状之后的症状可能是由产生初始症状的错误引起的. 一般来说,具有相同初始症状冲突集的反例越多,其错误越容易被诊断;反例中的症状数越少,其错误越容易被诊断. 因此,在诊断过程中,可按照初始症状冲突集的可疑度降序分析其中的转换. 初始症状冲突集的可疑度计算方法为
(1)
式中:SSC(e0)表示初始症状冲突集的可疑度;FSC(e0)表示包含初始症状冲突集SC(e0)的反例个数;FT表示总的反例个数.
转换可疑度的计算基于这样一个常理:出现次数越多,越容易被发现.初始症状冲突集中每个转换的可疑度计算方法为
(2)

式(2)在Tarantula公式基础上进行了改进.由定义可知,初始症状是测试用例中第1个出现错误的位置,该位置的转换发生错误的可能性最大,其次是初始症状之前的转换.在初始症状冲突集中,转换t距离初始症状越近,系数r值越大,可疑度就越大,表明发生错误的可能性越大.
2.2 诊断步骤
多错误诊断模型如图1所示,具体包括以下几个步骤.

图1 多错误诊断模型Fig.1 Multiple-fault diagnosis model
1) 比较预期输出和实际输出,将测试集分为证例和反例,生成症状和初始症状,并为每个初始症状产生冲突集及冲突序列.
2) 生成初始诊断集. 求所有初始症状冲突集的交集,作为初始诊断集. 如果初始诊断集不为空,则表明系统错误就在初始诊断集中.
3) 初始聚类,并计算可疑度. 若初始诊断集不为空,则计算初始诊断集中各转换的可疑度;若初始诊断集为空,则将具有相同初始症状冲突集的反例聚类成簇,按照可疑度计算公式计算每簇的初始症状冲突集及其所有转换的可疑度.
4) 错误诊断
错误诊断过程主要是执行如下步骤:
① 枚举错误转换组合.
② 枚举该组合的所有错误可能.
③ 用测试集验证错误可能,若验证通过,则诊断结束;若验证不通过,则再次进行枚举、验证,直到诊断成功或所有错误组合全部验证完毕.
枚举错误转换组合时遵循以下原则:
① 每一次选择转换时,选择未被选择过的、可疑度最大的初始症状冲突集中可疑度最大的转换.
② 若错误转换组合为t1,t2,…,tn,则ti为不包含t1,t2,…,ti-1的初始症状冲突集中的转换,其中n最大为初始聚类的类别个数.
枚举每个转换的错误可能有如下2种情况:
① 如果该转换是某个初始症状冲突集的初始症状,则枚举其输出错误,错误的输出可能是输出集合中除了正确输出值之外的其他任一输出值.
② 如果该转换在某个初始症状冲突集中,但不是初始症状,则枚举其转换错误,转换错误指的是尾状态错误,错误的尾状态可能是状态集中除了正确的尾状态之外的其他任一状态.
用测试集验证这些错误可能,这里有2种情况:
① 若错误可能使得测试集得到的输出与系统的实际输出相符,则计算修正该错误后的测试集输出,与期望输出进行比较,结果分为2种情况:若修正该错误后的测试集输出与期望输出相符,则表明错误已成功诊断;若修正该错误后的测试集输出与期望输出不相符,则表明还存在其他错误,因此,在修正目前诊断的错误后,转至1),进行剩余错误的诊断.
② 若错误可能使得测试集得到的输出与系统的实际输出不相符,则首先观察证例的输出与实际输出是否相符. 若不相符,则排除该错误;若相符,则计算该错误对初始症状冲突序列的输出. 若初始症状冲突序列的输出与其实际输出相符,则计算修正该错误后对初始症状冲突序列的输出,与其期望输出进行比较. 若输出与期望输出相符,则同样表明还存在其他错误,因此,在修正目前诊断的错误后,转至1),进行剩余错误的诊断.
5) 若上述过程无法得到确定的错误诊断集,则需要在初始症状冲突集之后的转换中进行枚举,或者增加一些测试用例再按照本文方法进行诊断.
2.3 与单错误诊断方法的比较
在单错误诊断方法中,比较经典的是文献[11]提出的Ghedamsi算法以及文献[12]提出的基于Ghedamsi算法的改进算法. 本文方法是在这2种方法基础上,结合聚类分析方法提出的一种多错误诊断方法. 该方法基于与单错误诊断方法相同的2个假设:假设错误只有转换错误和输出错误2种;假设一个转换只发生一种错误.
文献[12]在得到初始诊断集后,会依次对初始诊断集中的每个转换进行错误枚举,而本文方法则会首先计算初始诊断集中每个转换的可疑度,然后按照可疑度高低进行错误枚举,在这一点上分析效率要比文献[12]高. 不过文献[12]是基于单错误的诊断方法,在错误枚举时还结合了尾状态的下一转换提供的信息,可快速排除一些枚举项,而在多错误情况下无法利用这些信息,因为无法确定这些信息是否正确.
3 实例验证
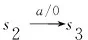

图2 一个有限状态机示例的描述及其实现Fig.2 Description and implementation of an example of FSM

表1 有限状态机示例的UIO序列
1) 生成初始症状及其冲突集
如图2、表2所示,比较测试序列的预期输出和实际输出,可知c1、c4和c10为证例,其余为反例.

表2 测试序列集的预期输出和实际输出
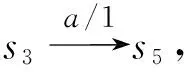

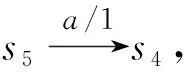
2) 生成初始诊断集
根据初始症状冲突集生成初始诊断集,ITC=SC1∩SC2∩SC3∩SC4=∅,初始诊断集为空.
3) 初始聚类,并计算可疑度
将具有相同初始症状冲突集的反例及所有证例聚类成簇
C1={c1,c4,c10,c2,c7}
C2={c1,c4,c10,c3}
C3={c1,c4,c10,c5,c8,c11,c12}
C4={c1,c4,c10,c6,c9}
根据式(1),通过计算得到每类初始症状冲突集的可疑度如表3所示.

表3 初始症状冲突序列覆盖向量及可疑度
根据式(2),通过计算得到每类初始症状冲突集中转换的可疑度如表4所示.

表4 初始症状冲突集中转换的可疑度
4) 错误诊断




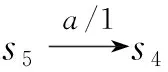
由上述过程可知,该例中运用本文方法只需枚举2个转换组合的错误可能,即可获得确定的错误诊断集.
4 实验分析
基于FSM的错误诊断方法主要在于如何充分利用已有信息有效地减少枚举数量,从而获得错误诊断集.
从第3节实例中可知,一个转换的错误可能个数与状态集和输出集大小成正相关. 为了验证诊断算法的有效性,构建5个FSM模型进行验证,如图3所示. 这5个FSM模型的状态数、输入/输出个数和转换数分别为(3,2,2,6)、(3,3,2,9)、(3,2,3,9)、(5,2,2,10)、(6,2,2,12). 对每一个FSM模型,枚举其1~3个错误的所有可能,表5列出了错误转换个数及其转换集中的占比.

表5 FSM及错误个数和错误占比
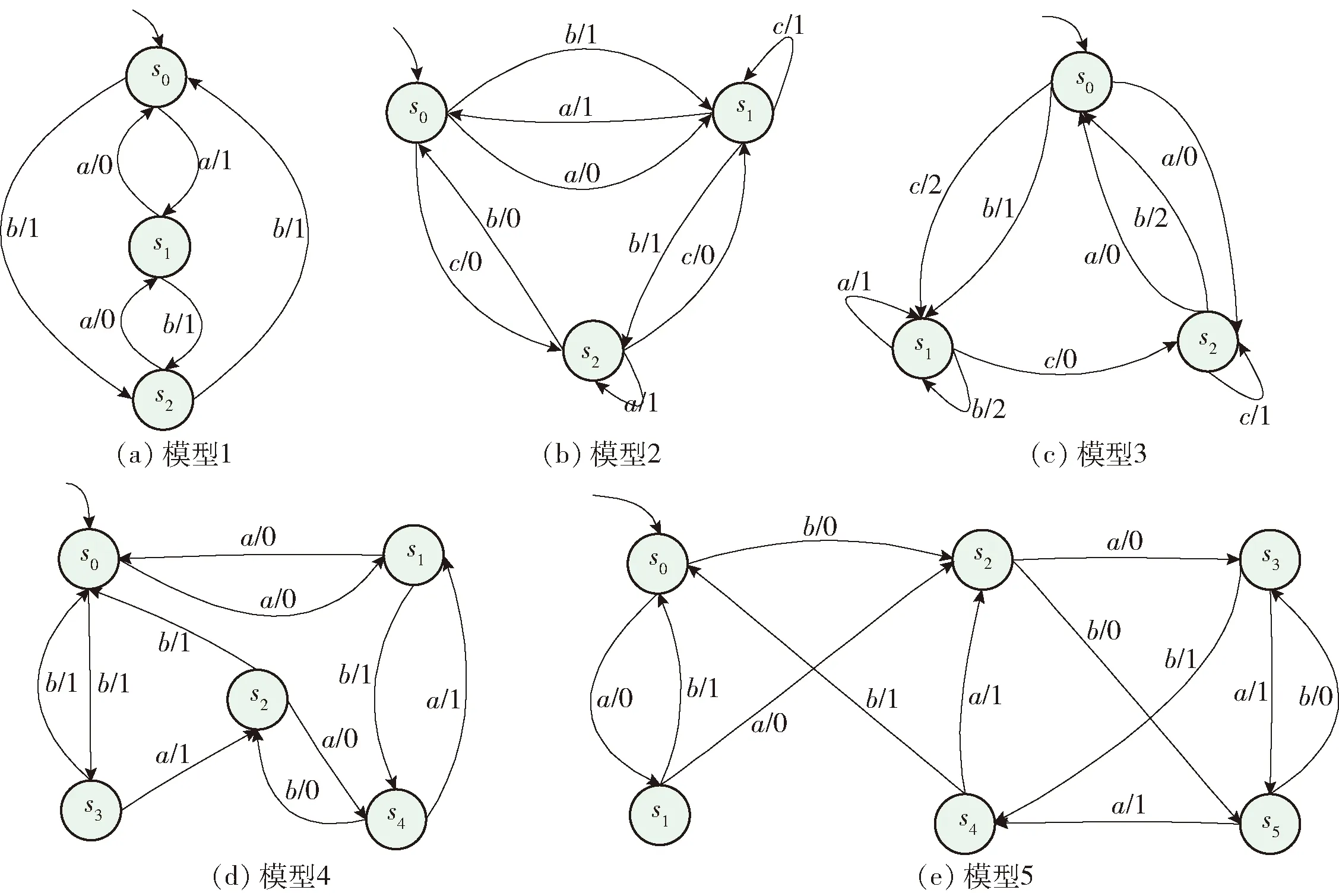
图3 实验集Fig.3 Experimental set
4.1 评价指标
1) 错误诊断率
枚举所有错误可能,依次诊断,当错误诊断集与错误集相同时表示诊断成功. 该指标为诊断成功的个数占所有错误可能的百分比,公式为

(3)
式中:P表示错误诊断率;NS表示诊断成功的个数;NT表示所有错误可能的个数.该指标表明了诊断算法的有效性.
2) 诊断代价
该指标为诊断成功前检查错误可能的个数占所有错误可能的百分比,公式为
(4)
式中:Q表示诊断代价;NC表示诊断成功前检查的错误个数.基于FSM的错误诊断要明确指出错误所在及错误原因,枚举错误的个数较为庞大,能够以较小的代价获得成功诊断,表明了诊断算法的可应用性.
4.2 实验结果分析
4.2.1 错误诊断率
图4是本文算法诊断1个错误、2个错误和3个错误的错误诊断率. 由图可知,错误诊断率与错误数量成负相关,也就是说诊断错误的成功率会随着错误数量的增加而降低. 图中显示3个错误的错误诊断率为86.50%~93.74%,而1个错误的错误诊断率则基本是100.00%,只有模型4的错误诊断率是92.00%.
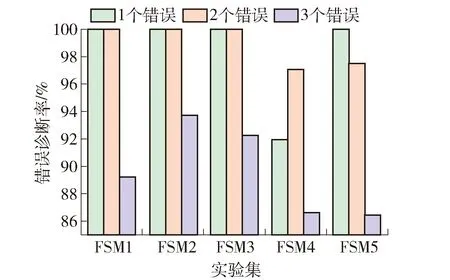
图4 错误诊断率Fig.4 Fault diagnosis rate
影响本文方法错误诊断率的因素主要有3个.
1) 与FSM模型本身有关,如表6所示的2个模型是具有相同状态集和输入/输出集,并且转换个数相同,但转换函数不同. 采用同一种测试集生成算法生成测试集,然后应用本文算法进行错误诊断,表6数据显示错误诊断率和诊断成功需枚举错误个数都是有差别的.

表6 不同转换函数对错误诊断率的影响
2) 与测试集相关. 图3中对FSM4诊断1个错误的错误诊断率为92.00%,实验显示有4个错误未被诊断出,设计实验分析诊断失败原因,发现在这4个错误情况下,测试集的所有用例的实际输出均等于期望输出,也就是说均没有反例. 没有反例就不存在症状,本文算法也无法应用. 表7的实验是基于相同的模型,而测试集分别由2种算法生成,一种是部分W(part of W,Wp)算法,一种是UIO算法. 表7显示不同测试集下的错误诊断率和诊断成功需枚举的错误个数,实验结果表明,无论是错误诊断率还是诊断代价都是有区别的. 基于UIO测试集的错误诊断率偏低,但多个错误的诊断代价略小.

表7 不同测试集对错误诊断率的影响
3) 与算法本身相关. 若聚类算法能够使得每类只包含1个错误,那么本文算法错误诊断率必定为100.00%. 但本文算法只是枚举了初始症状冲突集中转换的错误可能组合,没有枚举所有转换. 在现有测试集基础上,若初始症状冲突集不能够包含所有错误转换,则无法诊断成功. 例如,当前错误的尾状态是后续错误的头状态时,往往会出现假证例现象. 假证例使得初始症状冲突集不能够包含所有错误转换,本文算法则无法成功诊断出错误原因.
4.2.2 诊断代价
诊断代价反映了错误诊断的效率. 基于FSM的错误诊断方法其实就是枚举并验证错误可能. 若能穷举所有的错误可能,则必定可以诊断成功,但代价太大. 图5是盒图,显示了5个模型基于Wp测试集的平均诊断代价、最大值和最小值. 本文算法基本上可以在只枚举12%以内的错误可能情况下,以75%以上的成功率诊断出高达50%的错误转换及原因所在,说明该方法具有应用价值.
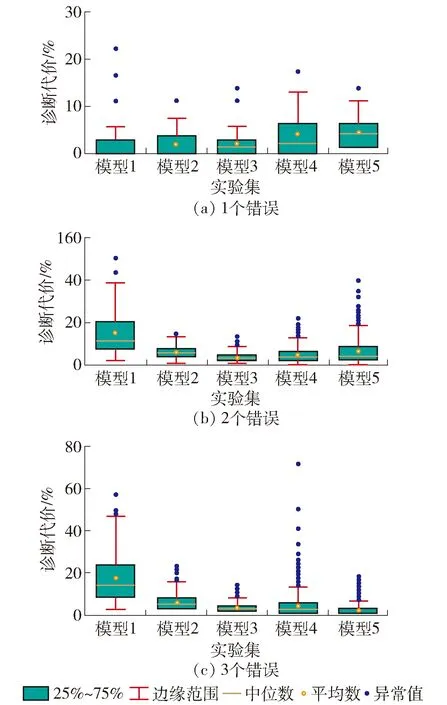
图5 诊断代价范围Fig.5 Diagnosis cost range
5 结论
1) 本文提出了一种基于FSM的多错误诊断方法. 现阶段针对多错误的研究主要集中在软件代码上且主要在如何定位错误,而本文方法可适用于采用FSM模型进行测试的系统,诊断结果不仅会给出错误所在,而且会指出错误原因.
2) 本文利用动态聚类分析方法解决多错误诊断问题. 首先,将反例按照初始症状冲突集相同与否进行聚类,并计算初始症状冲突集及其中转换的可疑度. 然后,选取高可疑的转换进行错误诊断分析,枚举可能发生错误的转换组合及其错误可能. 枚举错误组合时进行再次聚类,原则是错误组合中的转换不在同一个初始症状冲突集中. 最后,用测试集验证错误可能,若修正错误后符合期望输出则表示诊断成功.
3) 实例及实验结果表明,本文方法可以有效减少错误枚举数量,并且在不需要额外枚举或者增加测试用例情况下可以较低的诊断代价和较高的错误诊断率获得确定的错误诊断集.
4) 如果一个FSM有n种错误,在实际应用中只需要最多枚举n种错误即可获得诊断结果. 但由于实验需要验证方法的错误诊断率,枚举的工作量相当于nn,在单机实验中耗时较长,因此,文中实验的FSM规模较小,错误数也仅在3个之内. 下一步研究工作将改进实验的硬件环境,优化实验程序,进行规模更大的实验.

