铌酸锂薄膜调制器的协同仿真与优化设计

杨登才，陈雨康，王云新，向美华，陈智宇，刘萍萍，兰 天

(1.北京工业大学材料与制造学部激光工程研究院，北京 100124； 2.北京工业大学理学部物理与光电学院，北京 100124；3.中国电子科技集团第29研究所电子信息控制重点实验室，成都 610036)

铌酸锂(lithium niobate, LN)材料具有电光系数大、光谱响应范围宽和加工工艺技术成熟的优点[1-2]，在光纤通信、光纤陀螺等领域得到了广泛应用[2]. 传统的铌酸锂强度调制器采用质子交换或者钛扩散的方法制备光波导[1-5]，由于掺杂部分的铌酸锂与无掺杂的铌酸锂衬底折射率差很小，约为0.007，导致光模场直径为9 μm左右. 为了避免两波导发生模式耦合，通常要求调制电极之间具有较大的间距，这就间接降低了电光作用强度. 在1.55 μm的工作波长下，传统铌酸锂强度调制器的半波电压与电极长度乘积一般在10 V·cm以上[4-5].

近年来，由于铌酸锂薄膜工艺的突破，绝缘体上铌酸锂(lithium niobate on insulator，LNOI)结构调制器逐渐成为研究热点. LNOI基片的衬底材料为硅或者铌酸锂，衬底上生长了一定厚度的二氧化硅，二氧化硅层表面键合着一层薄薄的铌酸锂单晶薄膜[6]. LNOI结构波导主要是通过刻蚀或腐蚀工艺加工铌酸锂薄膜形成脊形波导. 脊型波导与二氧化硅包层的折射率差为0.7左右，更大的折射率差能获得尺寸更小的导模，光模场直径约为1 μm[7]，这样能极大地减小电极间距，增大电光作用效率. 目前，国内外报道的基于铌酸锂薄膜的电光调制器，半波电压长度乘积达到了2.2 V·cm[8-10]，1 cm电极长度下电光调制带宽达到了70 GHz以上[11]，这些性能参数均大大优于传统铌酸锂调制器. 同时，新的衬底结构要求相匹配的电极结构，才能获得更低半波电压并提高调制带宽. 然而目前尚未见专门针对LNOI结构的调制电极进行优化设计的相关报道[8，10-15]. 本文基于有限元方法，对基于铌酸锂薄膜强度调制器的电极结构进行了深入分析和优化设计. 该研究对LNOI结构的电光调制器的电极设计具有重要的指导意义.

1 电极结构分析

马赫增德尔(Mach-Zehnder，MZ)强度调制器利用电极施加电压信号来改变调制臂光波相位，两臂干涉后实现输出光强的调制功能. 输出光强最大和最小时对应的电压差即为半波电压[16]，可表示为

(1)

式中:λ为光波长；g为电极间距；ne为e光折射率；γ33为晶体z轴电光系数；l为电极长度；Γ为电光重叠积分因子[10]，可以表示为

(2)

式中：V为外加电压；E(x,y)为微波场分布；Eo(x,y)为光模场分布.

频率响应函数H(f)的表达式[17]为

(3)

式中：ε为相速失配因子，ε=2πf(neff-no)/c，neff为介质中微波的有效折射率，统一简称为微波折射率，neff=cβ/ω，β为相位常数，ω为角频率，c为真空中的光速，no为铌酸锂介质中光的有效折射率；α为微波衰减系数，包括导体损耗和介质损耗，Np/m.

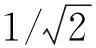
与集总电极相比，行波电极结构具有调制带宽大的特点，所以本文以行波电极结构为对象进行分析.为了避免微波反射，需要进行阻抗匹配，即行波电极特性阻抗要接近50 Ω负载阻抗.行波电极的特性阻抗Z0[18]为

(4)

式中R、L、G、C分别为行波电极的等效电阻、电感、电导和电容.

综上所述，在给定电极长度和电极间距的条件下，调制器的半波电压Vπ主要由电光重叠积分Γ决定；调制带宽Δf主要由介质中的微波折射率neff和衰减系数α决定.回波损耗主要由特性阻抗Z0决定.要得到上述调制器特征参数，需要对强度调制器的调制臂建模进行截面分析和频率扫描分析.

2 模型建立

2.1 整体模型

为了实现宽带宽调制，调制器的电极通常采用共面波导(coplanar waveguide，CPW)行波电极结构，其建模基于传输线结构.图1(a)显示的是铌酸锂MZ调制器内部的电极俯视图，可以看到，电极主要分为调制区和过渡连接区，其中调制区决定了器件的半波电压和带宽.调制器的截面模型如图1(b)所示.图中黄色部分代表电极，电极材料为金，中间为信号电极(S)，两边为地电极(G)，红色部分为二氧化硅，青色部分为铌酸锂薄膜刻蚀后的脊波导结构，橘黄色部分为硅衬底.截面参数主要有：信号电极宽度w、电极厚度t、电极间距g、上包层厚度tu和下包层厚度td.

图1 CPW行波电极结构Fig.1 Structure of CPW traveling wave electrode

2.2 协同仿真流程

利用COMSOL集团的COMSOL Multiphysics多物理场仿真软件和ANSYS公司的HFSS高频电磁场仿真软件进行协同仿真设计，仿真流程如下.

1) 从电极截面出发，建好截面模型后，利用COMSOL软件提取CPW行波电极的R、L、G、C分布参数，计算得到微波有效折射率、特性阻抗和微波衰减系数；同时进行模式分析得到波导内的光模场分布，进而求得电光重叠积分.

2) 对电极的厚度t、电极宽度w、多电极间距g、上包层厚度tu和下包层厚度td进行参数化扫描，优化得到一组综合性能指标最优的电极参数.

3) 利用优化得到的电极参数在HFSS中建立三维传输线模型，设置波导端口激励和网格后，进行频率扫描，可以计算得到电极的S参数.

该协同仿真模型中，截面二维模型利用COMSOL软件计算，复杂的三维模型利用HFSS软件计算，发挥了各个软件的优势，具有求解速度快、节省计算机资源的优点.

3 电极优化设计

3.1 模型验证

在上述建模基础上，完成电极设计，通过实验验证仿真方法的有效性.首先根据文献[10]中的电极参数进行仿真，并将仿真结果(simulation result,SR)和实验结果(experimental results,ER)进行了比较，电场和光模场分布如图2所示，其中左侧颜色栏表示光模场强度，右侧颜色栏表示电场强度。实验脊波导参数为：脊顶部宽度1.0 μm，脊厚0.3 μm，脊下薄膜层厚度0.3 μm，倾角75°.可以得到，单模光斑较好地束缚在脊波导里，且波导内的电场作用分布较强.仿真和实验数据对比如表1所示，半波电压与电极长度乘积的实验结果略大于仿真结果，在误差允许范围内；特性阻抗和微波有效折射率的仿真结果和实验结果非常接近，验证了上述方法建模的有效性.

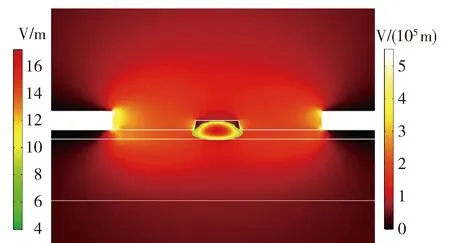
图2 电场和光模场分布Fig.2 Distribution of electric field and optical mode field

表1 实验结果与仿真结果比较

利用该模型进行优化设计.根据经验数据和实际工艺条件[8，10，19-20]，本文仿真条件设置如下：光波长为1.55 μm，微波信号频率设为20 GHz，电极宽度的扫描范围为5～30 μm，步长为2 μm，初始电极宽度为13 μm；电极厚度的扫描范围设为0.6～5.0 μm，步长为0.4 μm，初始电极厚度为1 μm；电极间距的扫描范围设为3～10 μm，步长为1 μm，初始电极间距为5 μm；下包层的扫描范围设为1～2 μm，步长为0.2 μm，初始下包层厚度为1.6 μm；上包层的扫描范围设为0～2 μm，步长为0.2 μm，初始上包层厚度为0.3 μm.

3.2 电光重叠积分

根据式(1)可得，电光重叠积分越大，半波电压越小.分析不同电极间距下，电光重叠积分的变化情况.将式(1)做如下变换

(5)

式中Γ/g为重叠积分与电极间距之比.

由式(5)可以得到，半波电压随Γ/g的增大而减小.设置电极宽度、电极厚度、下包层厚度和上包层厚度参数为初始值，对电极间距进行扫描，得到Γ/g随电极间距的变化，仿真结果如图3(a)所示.可以看出，电极间距越小，Γ/g越大，表明电极间距减小，模场处的电场强度增强，而电极宽度的变化不会引起电极间电场的变化.

此外，电极厚度和上、下包层厚度对电极间电场分布均有一定的影响.不同下包层厚度下，电光重叠积分随电极厚度的变化如图3(b)所示.仿真时设置电极宽度、电极间距和上包层厚度为初始值，不同下包层厚度下对电极厚度进行扫描.当下包层厚度为定值时，随着电极厚度的增大，电光重叠积分快速增大，电极厚度从0.6 μm增加到3.0 μm时，重叠积分增幅为8.6%，当电极厚度大于3.0 μm之后，曲线趋于平缓，变化小于0.1%，即模场处快速增大的电场此后基本趋于稳定，电极厚度最优取值不低于3.0 μm，以得到较大的重叠积分；当给定电极厚度，下包层厚度从1.0 μm增加到2.0 μm的过程中，电光重叠积分逐渐增大，增幅约为3.4%.

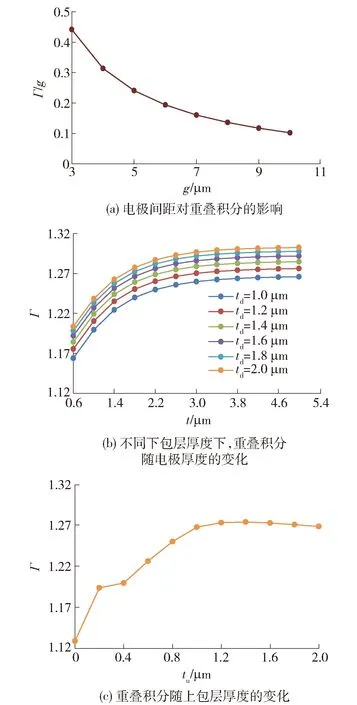
图3 电极参数对电光重叠积分的影响Fig.3 Influence of electrode parameters on electro-optic overlap integration

设置电极宽度、电极间距、电极厚度和td参数为初始值，对tu进行扫描，分析电光重叠积分随上包层厚度的变化关系时，得到的变化曲线如图3(c)所示。没有覆盖上包层(tu=0)时，电光重叠积分处于最小值1.13；当覆盖上包层，并逐渐增加tu，但不超过电极厚度1.0 μm时，电极间分布的电场得到了一定的束缚，局部电场增大，电光重叠积分迅速提高了3.5%.当tu大于电极厚度1.0 μm时，电极间的电场束缚不再增强甚至开始减弱，所以电光重叠积分略有减小的趋势.因此，tu应不超过电极厚度.

3.3 微波折射率

首先，对电极宽度和电极间距进行扫描，得到不同电极间距下，微波折射率随电极宽度的变化如图4(a)所示.随着电极宽度的增加，微波折射率逐渐增大，当电极间距为7 μm时，电极宽度从10 μm增加到30 μm的过程中，微波折射率增幅最大为2.2%，另外电极间距从3 μm增加到6 μm的过程中，微波折射率逐渐减小，不同电极宽度下的减少幅度在3.0%～4.6%变化，电极间距大于6 μm之后微波折射率趋于不变.因此缩小电极宽度和增大电极间距，有利于降低微波折射率，而且增大电极间距的效果更为显著.

图4 电极参数对微波折射率的影响Fig.4 Influence of electrode parameters on microwave refractive index

此外，上下包层厚度和电极厚度的改变也会影响有效介电常数进而影响微波折射率.电极厚度和下包层厚度对微波折射率的影响如图4(b)所示，在仿真扫描范围内电极和下包层越厚，微波折射率越低，在电极厚度从0.6 μm增加到5.0 μm时，微波折射率降低了9.4%左右，下包层厚度从1.0 μm增加到2.0 μm时，微波折射率降低了5.4%左右.上包层厚度对微波折射率的影响如图4(c)所示.微波折射率随着上包层厚度的增加而增加，厚度从0增加到2.0 μm时，微波折射率增加了6.8%.因此，增加电极厚度和下包层厚度，减小上包层厚度，有助于降低微波折射率.

3.4 微波衰减系数

影响带宽的另一因素是电极的微波衰减系数，衰减系数越小，带宽越大.衰减系数由导体损耗和介质损耗共同决定.导体损耗源于导线阻抗对电流的消耗，由于射频信号的趋肤效应，导致电流损耗变大；介质损耗源于介质的极化，交流电场使介质中电偶极子极化方向不断变化，消耗能量.

首先分析电极宽度和电极间距对衰减系数的影响.不同电极间距下，衰减系数随电极宽度的变化如图5(a)所示.电极宽度增大时，电极截面变大，阻抗减小，导体损耗也将减小，而介质损耗近似不变，所以衰减系数减小，当电极间距增大时，局部电场减弱，介质极化变弱，介质损耗将减小，而导体损耗近似不变，所以衰减系数也减小，这与图中曲线的变化趋势十分契合.因此增大电极宽度和电极间距有助于减小微波衰减.

其次分析电极厚度的变化与电极宽度的变化类似，随着电极的加厚，电极截面变大，导体损耗减小，而介质损耗不变，所以衰减系数将减小，如图5(b)所示.从图中还注意到电极厚度大于3倍趋肤深度(1.65 μm)时，剧烈下降的衰减系数开始趋于平缓；另外下包层厚度增大时，介质损耗稍有降低，衰减系数略有减小.所以增大电极厚度和下包层厚度有利于降低微波衰减.

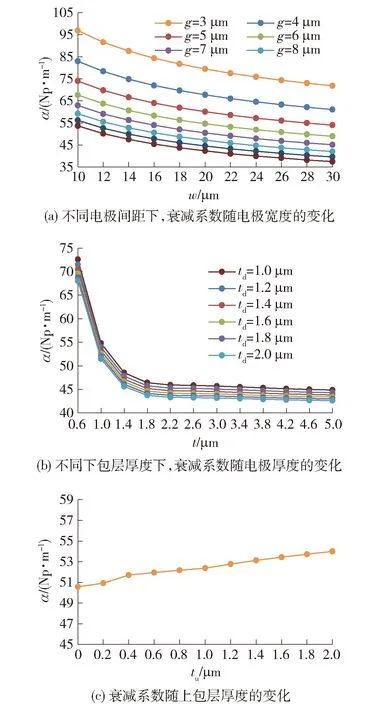
图5 电极参数对衰减系数的影响Fig.5 Influence of electrode parameters on attenuation coefficient

最后分析衰减系数随上包层厚度的变化，如图5(c)所示.随着上包层厚度的增加，电极间电场强度变大，介电损耗将增大，所以衰减系数也有所增加.因此上包层越薄，衰减系数越小，仿真扫描范围内变化幅度小于6.5%.

3.5 特性阻抗

行波电极的特性阻抗与负载阻抗不匹配，即阻抗失配，会引起回波损耗.阻抗失配越小，即特性阻抗越接近负载阻抗，回波损耗越小.

首先分析不同电极间距下，特性阻抗随电极宽度的变化.根据前面的分析，电极宽度越宽，电极截面越大，所以特性阻抗将减小.电极间距越大，高频电信号与地电极的距离变大，所以特性阻抗将变大，仿真结果如图6(a)所示.

其次分析不同下包层厚度下特性阻抗随电极厚度的变化，如图6(b)所示.随着电极厚度的增加，电极截面变大，特性阻抗迅速减小.下包层厚度增大，阻抗略有增加.因此减小电极宽度，增大电极间距，减小电极厚度以及增大下包层厚度，有助于增大特性阻抗.

图6 电极参数对特性阻抗的影响Fig.6 Influence of electrode parameters on characteristic impedance

最后分析上包层厚度对特性阻抗的影响，如图6(c)所示.随着上包层的增厚，特性阻抗逐渐减小.因此减小上包层的厚度有利于增大特性阻抗，从2.0 μm厚度减小到0 μm，特性阻抗增大了6.2%.

3.6 优化分析

电极宽度、电极间距、电极厚度和上下包层厚度对各电极性能参数的影响十分复杂，无法同时达到最优值，所以它们的取值应该综合考虑.这里采用软件内置的多变量约束优化算法，把电极宽度、电极间距和电极厚度作为自变量，半波电压、微波有效折射率、微波衰减系数和特性阻抗作为因变量，暂时不覆盖上包层，首先设置下包层厚度为2.0 μm，在一定范围内随机改变自变量的值使得半波电压、微波衰减系数趋近最小值，微波有效折射率和特性阻抗分别趋近光模式有效折射率1.876和匹配阻抗50 Ω，经过数次迭代，得到了一组优化解，电极宽度、电极间距和电极厚度分别为6.0、6.0、6.0 μm，此时计算得到20 GHz下微波折射率为1.842，特性阻抗为46.6 Ω，半波电压为2.61 V，当覆盖厚度为0.4 μm的上包层时，模型分析得到光模式有效折射率为1.895，微波有效折射率为1.864，特性阻抗为46 Ω，相速匹配和阻抗匹配均良好，半波电压为2.45 V，降低了0.16 V.由于下包层的增厚对各表征参数均有利，因此接下来将下包层厚度设置为4.6 μm，重复优化求解步骤，得到新的一组优化解，电极宽度、电极厚度、电极间距参数分别为13.3、2.2、5.3 μm，在20 GHz下微波折射率为1.950，特性阻抗为49.2 Ω，半波电压降为2.35 V，当覆盖厚度为0.4 μm的上包层时，微波有效折射率为1.975，特性阻抗为48.8 Ω，半波电压为2.17 V，这表明在下包层厚度增加后，器件阻抗得到了更好的匹配，半波电压也得到了进一步降低.

LNOI结构电光调制器的调制波导可以采用干法或湿法刻蚀工艺，在LNOI衬底上刻蚀出脊型波导，目前哈佛大学、山东大学、中山大学等多个研究机构已经进行了深入的研究和探索[7,10-11]，并成功实现了铌酸锂薄膜波导的刻蚀.然后，通过蒸镀一定厚度的金电极实现调制电极的制备.蒸镀电极之前，在铌酸锂表面溅射一层几纳米的金属铬膜，用于增加金电极的黏附性，而这层铬膜对电极性能的影响很小，因此，分析时常忽略不计.最后，溅射一层二氧化硅作为脊波导的上包层，降低脊波导表面粗糙度带来的损耗.

接下来对4.6 μm下包层厚度下选定的参数建立片上行波电极模型，进行频率扫描分析.

4 高频特性分析

利用优化得到的电极参数在HFSS软件中建立三维CPW传输线模型，电极长度设为1 cm，对其进行频率扫描，扫描范围为0.1～75.0 GHz，步长0.1 GHz.

扫描得到电光S21(EO-S21)和电极回波损耗S11(E-S11)的频率响应曲线如图7所示.可以看出，3 dB调制带宽大于70 GHz，高频条件下的回波损耗整体低于-20 dB.

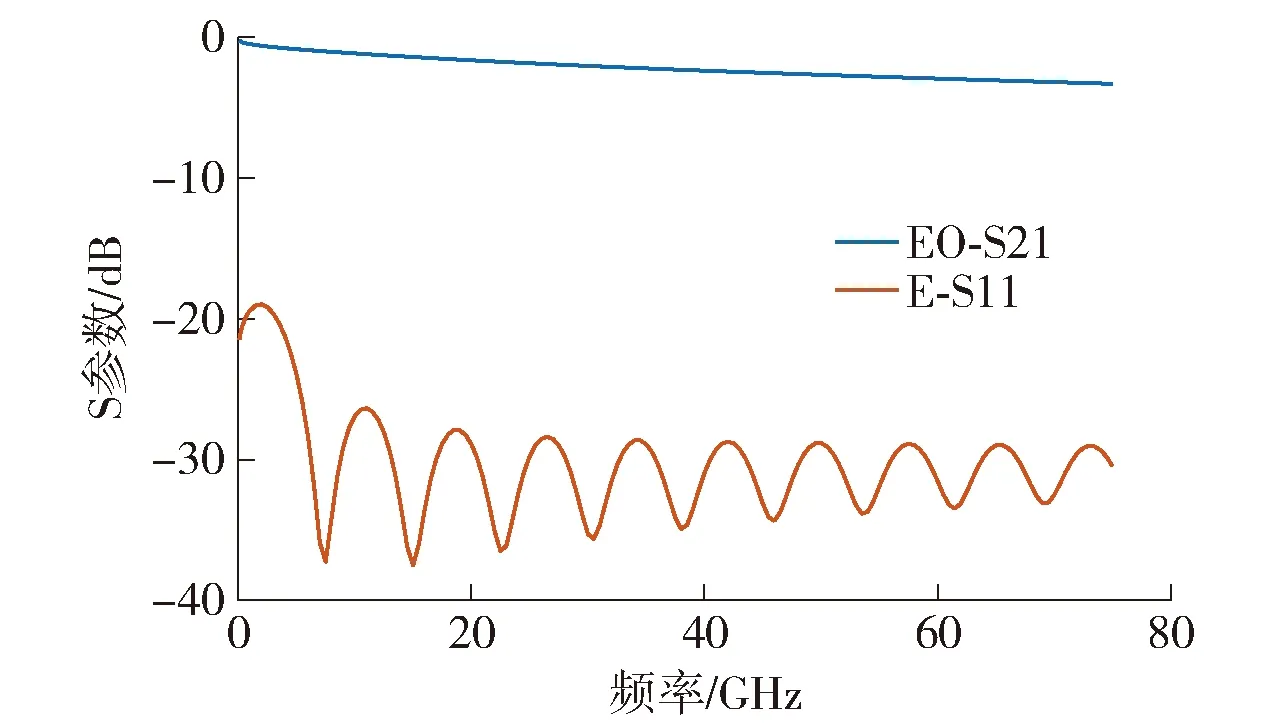
图7 行波电极的频率响应曲线Fig.7 Frequency response curve of traveling-wave electrode

5 结论

1) 仿真分析表明，脊上覆盖的上包层能够有效增大电光重叠积分，上包层越厚，电光重叠积分越大，当tu超过电极厚度时，重叠积分变化趋缓.然而，上包层的加厚会降低阻抗，增大微波折射率和微波损耗，不利于阻抗匹配和相速匹配，但是能够降低半波电压.因此，需要权衡考虑脊上覆盖的上包层的参数设计，兼顾半波电压、带宽等性能.

2) 随着td的增加，电光重叠积分和特性阻抗均增大，微波折射率和微波损耗均减小，既有利于降低半波电压和电极回波损耗，又能增大带宽，所以应在工艺允许范围内尽可能增加td.

3) 优化得到了一组电极参数，当电极长度为1 cm时，器件半波电压为2.17 V，3 dB带宽大于70 GHz，回波损耗在高频条件下整体低于-20 dB，达到了较好的优化设计结果.由于目前还没有针对这种新结构的电极分析的报道，因此本文的研究对基于LNOI结构电光调制器的电极设计具有重要的指导意义.