一类微分方程最佳平方逼近解法的注记
2021-06-15 02:42岑达康汪志波
佛山科学技术学院学报(自然科学版) 2021年3期
岑达康,汪志波
(广东工业大学 应用数学学院,广东 广州 510520)
定义1 对(fx)∈C[a,b]及C[a,b]中的一个子集φ=span{φ0(x),φ1(x),…,φn(x)},ρ(x)为非负函数,若存在S*(x)∈φ,使
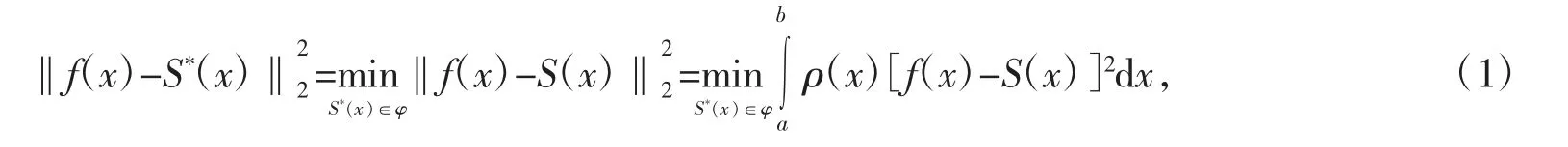
则称S*(x)是(fx)在子集φ⊂C[a,b]中的最佳平方逼近函数。
定理1[1]若S*(x)∈φ,其中φ0(x),φ1(x),…,φn(x)线性无关。记

可得S*(x)=[φ0φ1… φn]α=[φ0φ1… φn]A-1β,最佳平方逼近误差为C-β'A-1β。不妨以勒让德多项式[2]为基函数,给出一类微分方程数值解法。
1 勒让德多项式及性质

正交性,表示为

2 勒让德多项式逼近

3 微分方程数值求解


4 数值实验
例求解如下微分方程的数值解

方程的精确解为u(x)=x2+1。
数值实验采用Matlab2014a 进行运算。取权函数ρ(x)=1,基函数为{φ0,φ1,φ2}={1,x,3/2x2-1/2}。解得数值解U(x)=x2+x/180 143 985 094 819 84+1。平方逼近误差为(x/180 143 985 094 819 84)2dx=2.054 3e-33。
猜你喜欢
科学技术创新(2022年33期)2022-11-12
数学物理学报(2022年4期)2022-08-22
安庆师范大学学报(自然科学版)(2021年1期)2021-11-28
数学物理学报(2021年4期)2021-08-30
中学生数理化·高一版(2021年2期)2021-03-19
南京大学学报(数学半年刊)(2020年1期)2020-03-19
中央民族大学学报(自然科学版)(2018年3期)2018-11-09
航空学报(2018年9期)2018-09-29
吉林大学学报(理学版)(2018年4期)2018-07-19
遥测遥控(2015年2期)2015-04-23

