一类捕食者-食饵模型的分支分析
陆秀琴,温洁嫦
(广东工业大学 应用数学学院,广东 广州 510520)
食饵捕食者之间的动态关系一直是种群动力学模型的一个重要研究课题,众多学者对食饵捕食者系统进行研究并得到了大量的结论[1-10]。在种群动力学当中,许多的数学家和生物学家都对如下系统感兴趣

其中,x 为食饵的种群密度,y 为捕食者的种群密度,r,a,k,s,b 都是常数且为正,ax 为每一个捕食者捕食食饵的数量,r 为食饵的固有增长率,m 为环境容量,s 为捕食者的增长率,b 为反映捕食者种内竞争的正常数。
首先对模型(1)作如下变换

则可将模型(1)变为

虽然学者们对经典的捕食者食饵模型做了大量的研究,但还是有些许不足。例如文献[11]发现食饵对捕食者的恐惧会致使食饵后代的数量急剧减少,其原因是食饵的捕食风险对其出生率及其后代都有很明显的影响。而Wang 等[12]正是考虑到了食饵种群对捕食者种群的恐惧而导致食饵种群及其后代数量的急剧减少及捕食者-食饵模型由于恐惧产生反捕食的防御成本,从而对食饵种群的出生率引入恐惧效应因子(fk,v)=,其中v 为捕食者种群密度,k 为驱动食饵反捕食行为的恐惧程度的相关常数。
人们在研究生物种群时着重关注种群的演变规律和如何采取措施对种群进行合理开发利用和保护的问题,针对这些问题的研究,除了可以对种群的变化和发展进行探索分析和加以估计,学者们还可以建立具有食饵收获率的捕食者-食饵模型,然后对该模型进行分析,得出需要多少的食饵收获率才能使该捕食者食饵模型系统达到一个动态平衡且又可以满足人们的需求,因此研究具有收获率的捕食者食饵模型对生态保护和可持续发展具有重大意义。
受到文献[11-12]的启发,笔者引入恐惧因子(fk,v)=且加入食饵收获率于模型(2)中,即考虑具有常数收获率和恐惧效应的捕食者-食饵模型,首先给出系统模型平衡点的存在条件,然后主要讨论了平衡点的类型及稳定性和正平衡点的Hopf 分支,且得出了产生Hopf 分支的条件;最后,对该模型做了数值仿真模拟实验并得到了相关结论。
相应的常微分模型为

其中,k 表示恐惧程度,h 为捕食者对食饵的常数收获率。
1 平衡点的类型及正平衡点的稳定性
考虑到模型(1)的生物意义,所以之后的讨论都在u≥0,v≥0 上进行。首先考虑平衡点的存在性。令系统(3)右端为0,可得:

接下来讨论平衡点的类型及其稳定性,系统(3)的Jacobi 矩阵为
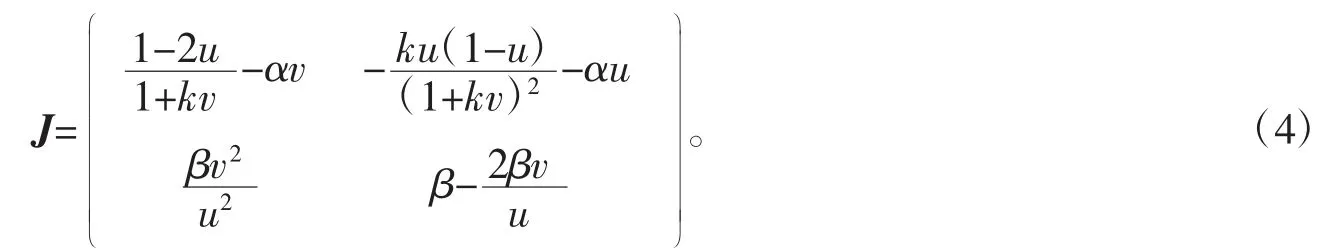
利用文献[13-14],通过计算可得如下结论:
(1)边界平衡点E0为高次奇点;
(2)边界平衡点E1为鞍结点;
(4)E3为高阶奇点,E4为鞍点,E5为非鞍初等奇点。
将平衡点E3,E4和E5代入Jacobi 矩阵(4)当中,计算系统(3)在平衡点处Jacobi的矩阵并讨论其特征值,利用文献[13-14]],可以得到以下结论:E3为高阶奇点,E4为鞍点,E5为非鞍初等奇点。
2 Hopf 分支
由上一节的讨论可以知道,当满足hk<1 并且L(u*)<0 的时候,系统(3)存在两个正的平衡点E4(u4,u4)和E5(u5,u5),其中E4为鞍点,E5为初等焦点或结点。下面讨论系统(3)在E5(u5,u5)附近的Hopf 分支。
系统(3)在E5(u5,u5)处的雅可比矩阵为
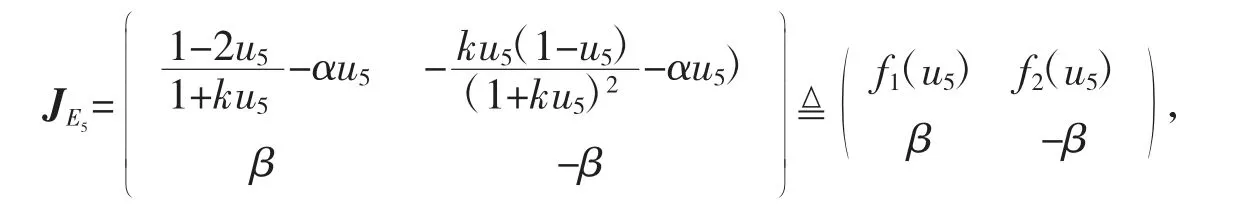
其中
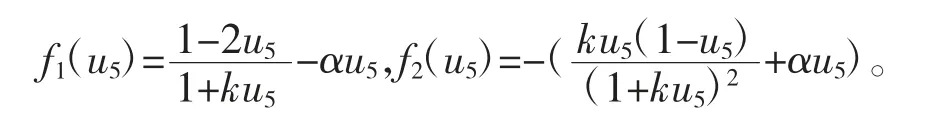
则该Jacobi 矩阵的特征方程为

则当f1(u5)=β 时,Jacobi矩阵JE5的特征方程(5)有一对纯虚的特征根±iω0(i 为虚数单位,ω0=
由于E5是系统(3)的一个平衡点及f1(u5)=β,可以得到
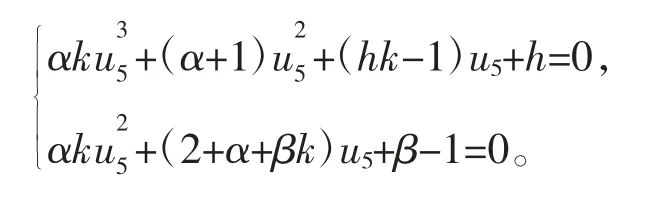
由辗转相除法,可以得到
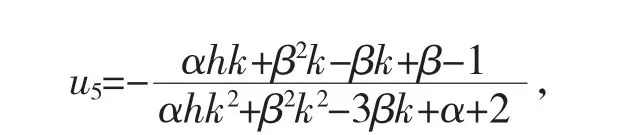
将u5代入αhu2+(2+α+βk)u+β-1=0 中,得到满足Jacobi矩阵JE5的特征根有一对纯虚根的条件β<1 且
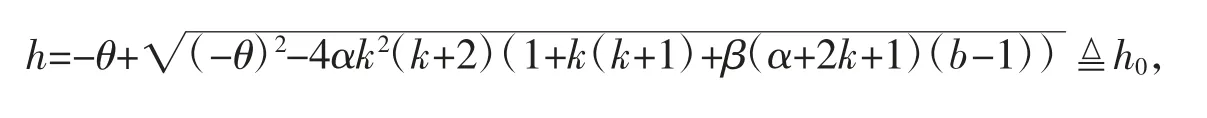
其中
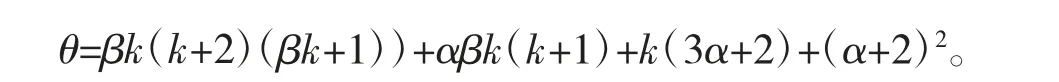
取h 为分支参数,设特征方程(5)的特征根为λ=p(h)+iω(h),得p(h)=0,ω(h)=ω0。根据L(u5)=0,L'(u5)>0,则由L(u5)=0 确定的隐函数的导数u5=u5(h)的导数为
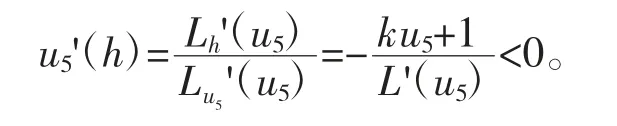

由p'(h)>0 可知系统(3)满足产生Hopf 分支的条件[15]。因此系统(3)在h=h0附近可产生Hopf 分支。接下来讨论产生的Hopf 分支的方向。
令ω1=u-u5,ω2=v-v5。则系统(3)变成以下形式

由L1(0)=,可以得到当l1(0)>0 时,模型(3)在E5附近可以产生次临界的Hopf 分支。
3 仿真算例
由上一节结论可知,若取α=2,β=0.2,k=1,通过Maple 软件可计算得h0=0.061 428 125 85,u5=0.175 765 067 0,v5=0.175 765 067 0,ω0=0.226 418 018 6,且可以算出L1(0)=193.875 767 6>0,那么系统(3)就会在h=h0处有次临界的Hopf 分支产生,当h 在小于h0附近取值时,则在平衡点E5附近存在唯一的不稳定极限环,如图1 所示。
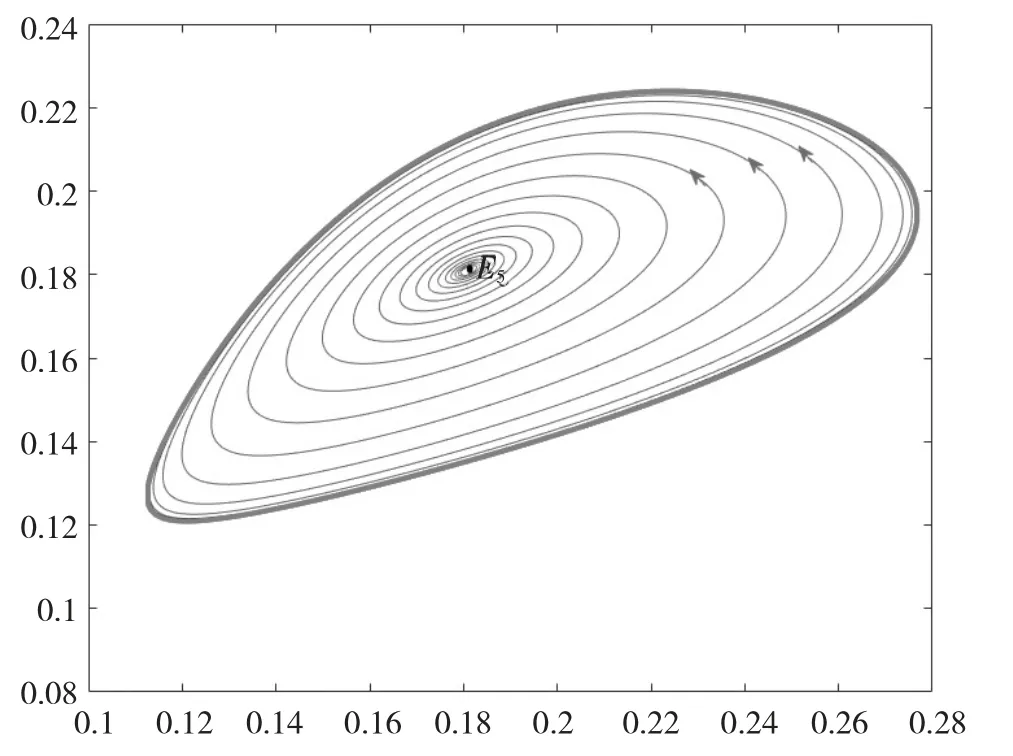
图1 在E5 附近存在不稳定极限环
4 结论
食饵对捕食者的恐惧效应可能会使食饵种群及其后代数量急剧减少,并且可能会导致捕食者-食饵模型由于恐惧产生反捕食的防御成本。而具有收获率的捕食者食饵模型对生态保护和可持续发展具有重大意义。本文主要针对模型(1)所研究模型,对食饵种群进一步增加常数收获率和恐怖效应后分析新的模型的平衡点类型及其稳定性和正平衡点的Hopf 分支,即讨论了一类食饵种群具有常数收获率和恐惧效应的捕食者-食饵模型的平衡点类型及其稳定性和正平衡点的Hopf 分支问题,且通过运用Matlab 软件和Matcont 软件作出了相应的Hopf 分支图。由上面的讨论可以知道,次临界的Hopf 分支可以产生不稳定的极限环,其中的参数和初值是通过适当的选取来获得,当初值处在不稳定的极限环里面时,轨线趋向于正平衡点,也就是说最终捕食者和食饵种群的数量趋于稳定而不会消失。

