基于数值变分计算的Acrobot 机器臂能量最优控制

李江成，詹清华，区国洪，何 俊

（1.广东省立胜技术有限公司，广东 佛山 528200；2.佛山科学技术学院机电工程与自动化学院，广东佛山 528225）

欠驱动机器臂包括肘部驱动（Acrobot）和肩部驱动（Pendubot）两种［1-2］，实际系统中Acrobot 模型由于有重力的存在，表现为2 阶微分约束系统，这类系统是可控的，因而从初始位置驱动系统至期望位置的控制问题理论上是可以实现的。近期出现了一类分区域控制欠驱动机器臂的方法，即将控制区域分为摇起区和吸引区，在吸引区线性化系统再采用线性系统理论稳定系统，需要指出的是Acrobot 是不可完全线性化的［3-4］，在控制器中加入扰动或者起始力矩来改变系统的初始状态达到控制目的，二者在摇起区的线性化策略从理论上是不可行的［5-10］。基于这方面的原因，智能控制的思想在本领域得到应用，本文将采用变分原理来研究Acrobot 的控制问题。

1 欠驱动机器臂Acrobot 动力模型

Acrobot 的模型结构如图1 所示。图1 中，mi（i=1，2）表示第i杆的质量，li表示第i 杆的长度，lci表示从i 关节到i 杆质心的距离，Ii表示第i 杆相对于质心的惯性，q1表示第一杆相对于垂直向上y 轴的角度，q2表示第二杆相对第一杆的角度，τ2为作用在第二连杆上的控制力，g 为重力加速度。

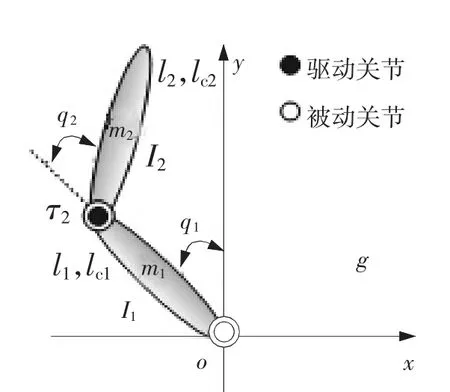
图1 Acrobot 的模型结构

令q=［q1，q2］·，Acrobot 的动力学方程满足

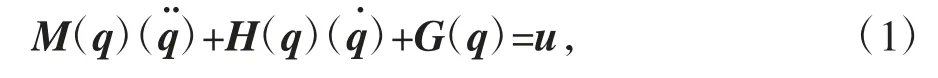
其中，

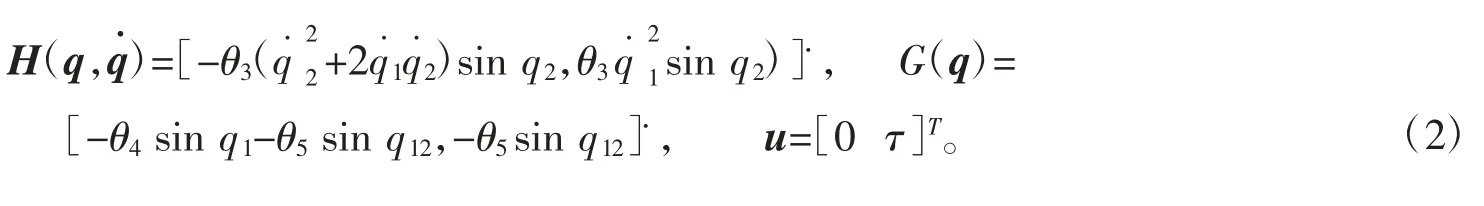
于是有

优化控制的前提是假定存在一种控制律，能够引导系统从初始状态运动至终端状态，文献［11-12］证明了存在一种控制器完成Acrobot 从平衡点到平衡点的切换。下面讨论系统从垂直向下平衡点到垂直顶点的最优控制器设计，这种情形性能指标中的被积函数的横截条件总是满足的。

2 最优控制问题描述

最优控制问题可描述为，对于给定系统（1）、初始状态x0=［-π 0 0 0］T以及终端状态xd，寻找合适的控制律τ，最小化目标函数为

其中，tf为终端时间，可以是事先给定的，也可以是未知的。

引理［13］无约束极值问题

J 取极值的必要条件为

由欧拉-拉格朗日原理，Acrobot 系统的优化目标函数为

即极小值问题为

记y=［x1x2x3x4λ1λ2λ3λ4］T∈R8，结合式（12）消去τ，则式（7）转换为

至此，完成了条件极值问题转换成为无条件极值问题。

对式（9）两边积分有

其中，c 为常数。为消除常数c，考虑下列积分

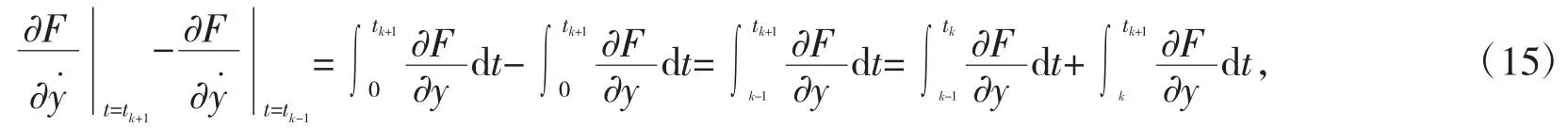
即得到递推公式

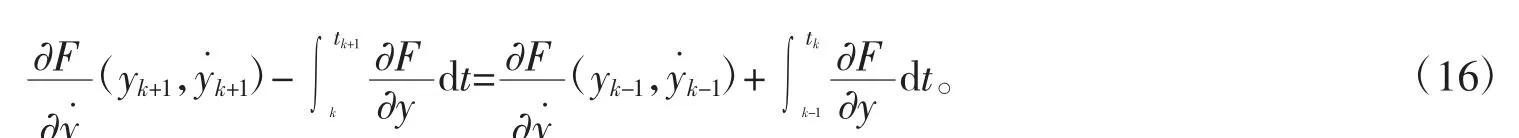
由式（16）可以看出，左端是k 时段末的状态函数，右端是已知的前二时段末状态函数。设；tk=kh，且k=1，2，…，n，其中n 为轨迹线细分段数。为简单起见，取中值计算式（16）各部分积分，有

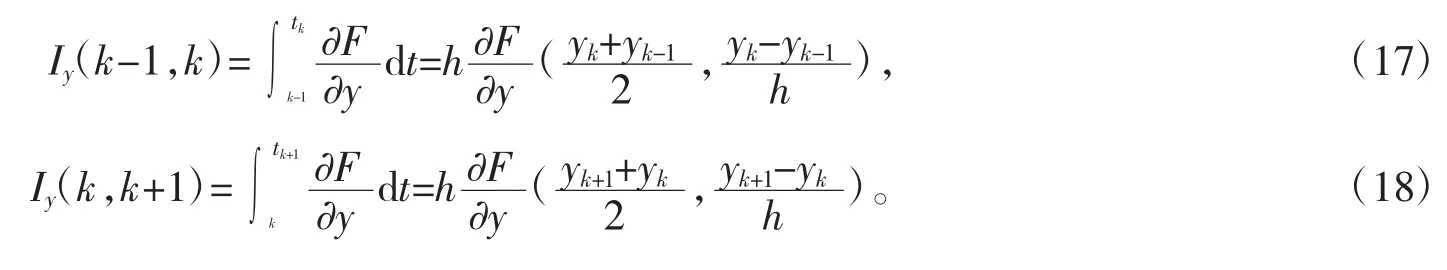
于是有

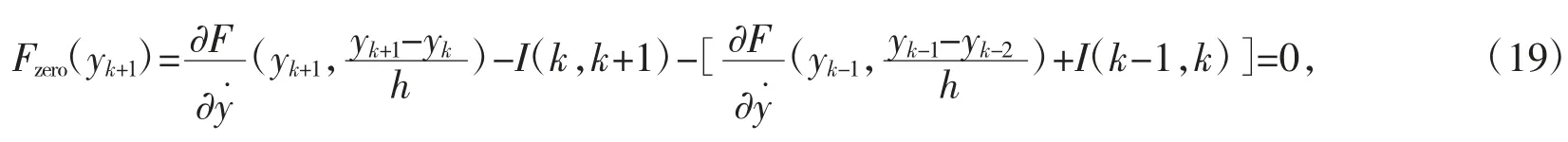
式（19）是含有8 个未知数的非线性方程，当初始条件给定后，可以递推求解时段末的状态。

3 仿真实例

在系统（1）中，设结构参数I1=I2=1 kg/m2，l1=l2=1 m，m1=m2=1 kg。初始条件和终端条件分别为x0=［-π 0 0 0］T，xd=［0 0 0 0］T。拉氏函数为

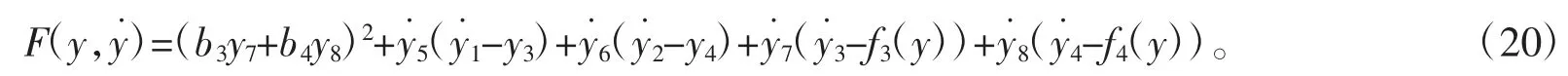
取tf=4 s，n=64，仿真结果如图2 所示。由图2 可知，系统在k=66 时稳定，即稳定时间约为4.06 s。

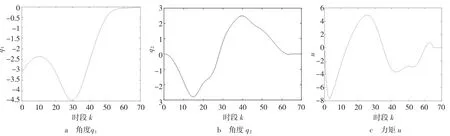
图2 角度及控制力矩仿真结果

4 小结

本文研究了肩部欠驱动双连杆机器臂的最小能量的控制问题，该问题被当作一无条件极值问题，优化目标采用数值求解技术来处理，所引进的乘子以时间导数出现，既改善性能指标的可积特性，简化了参数初始值的确定，仿真实例表明本文方法的有效性。因为Acrobot 在实际工程系统中（有重力的存在）是可控的，从指定任意位置达到状态空间中任意位置是可能的，这是进一步要研究的课题。