恶劣天气下多航空器改航路径的仿真优化算法*

朱承元 晏楠欣

（中国民航大学空中交通管理学院 天津300300）

0 引 言

21世纪的空中交通管制需要应用现代计算机科学与技术，以适应未来更多流动人口的航空旅行需求。对航空旅行吞吐量的最大挑战之一是恶劣天气的存在，它导致飞机的延误、取消和改道，而合理规划和优化恶劣天气下的改航路径是保障空域安全以及提升空域容量的有效途径之一。

目前，国内外已有不少学者研究了恶劣天气下的改航问题[1-2]，例如：Joseph Prete等[3-4]研究了基于流量的航线规划（flow-based route planner，FBRP）系统的算法，计算出避开时变危险天气，供飞机安全通过的最短航线。Christine Taylor等[5]利用模拟退火方法确定受天气影响的航班在运行上可接受的备选航线，实现更有效地使用空域。Jimmy Krozel等[6]将航线搜索算法应用于避让危险天气的改航问题，得到最优改航路径。Jimmy Krozel等[7]还研究了根据最新天气预报动态生成编码起飞航线（CDRs）的方法，利用考虑天气预报的算法生成这种天气避让路线。李雄等[8]在二维平面利用几何算法进行恶劣天气下的改航路径规划。赵元棣等[9]利用A*算法构建了静态和动态条件下的改航路径快速规划模型，提出了动态危险天气下的快速改航规划的方法。张兆宁等[10]提出利用多普勒雷达识别散点状分布危险天气区域，采用平顺曲线段和转角曲线段组合的方式，生成终端区动态改航路径。杜实等[11]通过构建实时动态环境模型，并利用多目标粒子群算法（multi-objective particle swarm optimization，MOPSO）对改航路径进行动态规划。

上述研究主要通过建立数学模型，进行约束限制，达到减少航班延误，降低运行成本或生成最优改航路径等目的，其效果良好，但上述模型中存在着变量的关联性复杂以及数学模型求解困难的问题，缺乏对管制员工作负荷的考虑，未将仿真模型和智能算法有效结合，不能有效的应用于实际工程之中。本文在保证航空器安全运行的前提下，考虑恶劣天气的动态变化和管制员工作负荷，借鉴FBRP方法的思想，考虑以随机搜索为特征的粒子群算法[12]（particle swarm optimization，PSO）的灵活性以及可在较短时间内找到最优解的特点，利用全空域与机场模型（total airspace and airport modeller，TAAM）结合几何算法和离散粒子群算法（discrete particle swarm optimization，DPSO），进行改航路径的规划与优化。

1 构建改航环境模型

1.1 划设飞行受限区

1）建立改航平面直角坐标系。选取恶劣天气左下方距离中心地带较近的某点作为原点，磁北方向设为y轴正方向，磁北偏东90°设为x轴正方向。

2）划设恶劣天气区域。选取降雨量≥13.3 mm/h的区域，即将在雷达显示图中呈现为黄色、橙色、淡红色及红色的区域作为初始恶劣天气区域，利用Matlab软件和平面点集凸包（Graham）算法[13]，进行灰度化处理和凸包划设，得到散点状分布的多个初始飞行受限区（flight forbidden area，FFA），见图1。

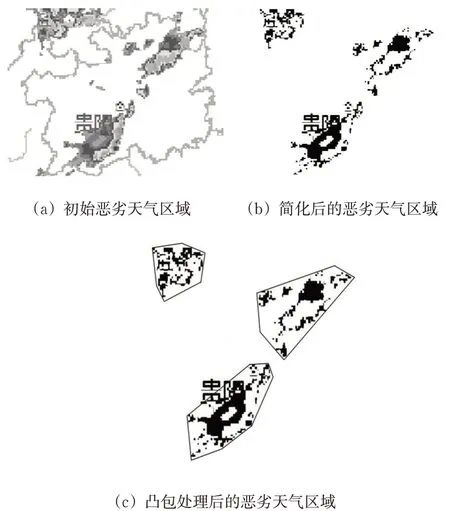
图1 划设初始飞行受限区Fig.1 Designation of the initial flight-forbidden area

1.2 预测飞行受限区

由于恶劣天气的移动具有随机性，因此，参考文献[14]中灰色模型预测飞行受限区，简化质心位置和边界坐标的计算，优化外推边界的计算。目的是简化计算，使恶劣天气的呈现更加动态化，同时缩小最终飞行受限区的范围。具体步骤如下。

1）明确观测时刻Ti(i=0，1，…，s)

2）明确质心位置

式中：v x=（xi-xi-1）/T，v y=(yi-yi-1)/T。

3）确定边界坐标

4）确定外推边界

2 改航路径的仿真优化算法

2.1 仿真优化算法的主体步骤

步骤1。依据初始FFA的范围，明确优化区域，确定初始方案，进行仿真建模。

步骤2。设航空器到达改航起始点的时刻为当前时刻，根据前一时刻和当前时刻的恶劣天气区域，以30 min为时间尺度，预测未来2 h的FFA"，在TAAM模型中建立相应的FFA"。

步骤3。利用几何算法规划多条改航路径，利用TAAM模型与Matlab软件进行建模和改航路径选择的优化，从TAAM模型链接的MySQL数据库中提取相关数据，计算多航空器对应的管制员工作总负荷和改航总路径距离。

步骤4。若满足迭代次数，则得到优化解，即恶劣天气下的多航空器的优化改航路径；反之，运行改进DPSO算法，进行新一轮优化计算，重复步骤3～4，直至得到多航空器的优化改航路径。

仿真优化算法的主要流程见图2。

2.2 改航路径的规划

规划改航路径的核心是设计多条可用的备选航线，并以改航路径最短为优先级，以增加既能避开FFA"又能减少交叉的路径总数为原则。

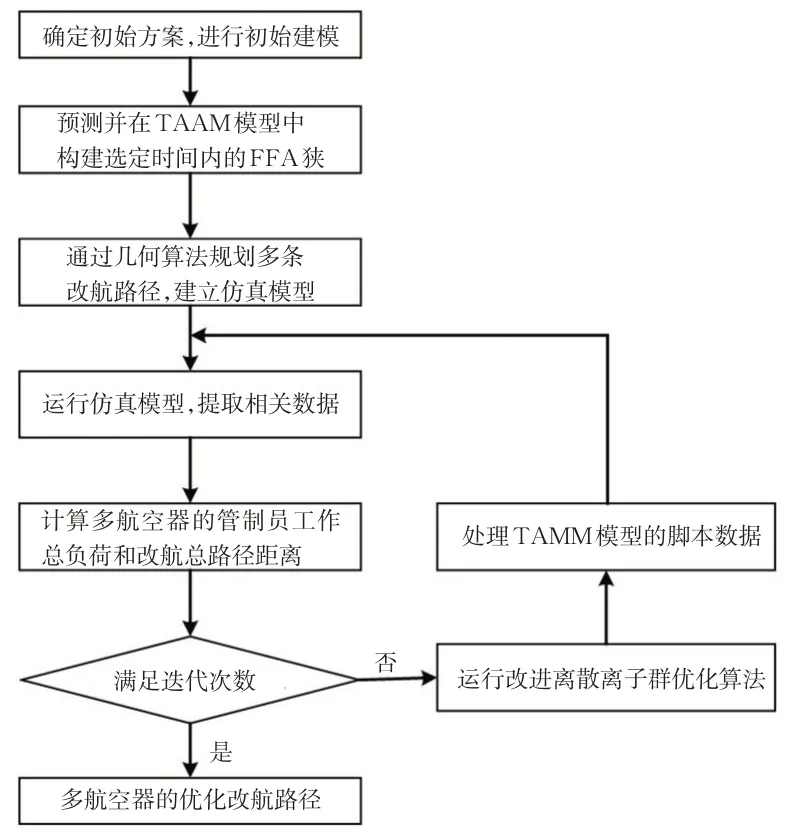
图2 仿真优化算法的流程图Fig.2 Flow of the simulated optimization algorithm

2.2.1 确定改航点

1）确定初始改航点。确定FFA"与原航线的交汇点（图3中的ge和g l），选取距离交汇点最近的航路点作为改航的始末点。

2）确定中间转弯点。

步骤1。将交汇点的连线作为分割线（图3中的l g o g f），取l go g f的中点gm，分别连接对应FFA"中距离g m最远的点，记为d r和d l。

步骤2。选取rmin=min{d r，d l}，过g m点作垂直于l g o g f的朝向rmin区域的射线l，以gm为圆心作圆弧，取圆弧和l的交点为中间转弯点g r；然后，考虑偏航角度和航段距离的约束，过g r做平行于原航线的直线l r，再取2个新的改航点g"r，g"r作为中间转弯点，而对应的改航始末点依照规划改航路径的原则，内移、外推或保持不变。其中，gr(xr，y r)确定见式（6）。

而g"r(x"r，y"r)、g"r(x"r，y"r)可参考文献[8]中改航点修正的计算。

步骤3。考虑不触发TCAS告警的最小距离间隔和航班潜在冲突[16]等因素，对航路进行分流，选取rmax=max{d r，d l}，重复类似步骤2的操作，得到中间转弯点g r1以及新改航点g"r1，g"r2，其坐标计算同上。

改航点的确定见图3。其中灰色区域表示初始FFA，黑色的虚线攘括的区域为外推边界后的FFA"。

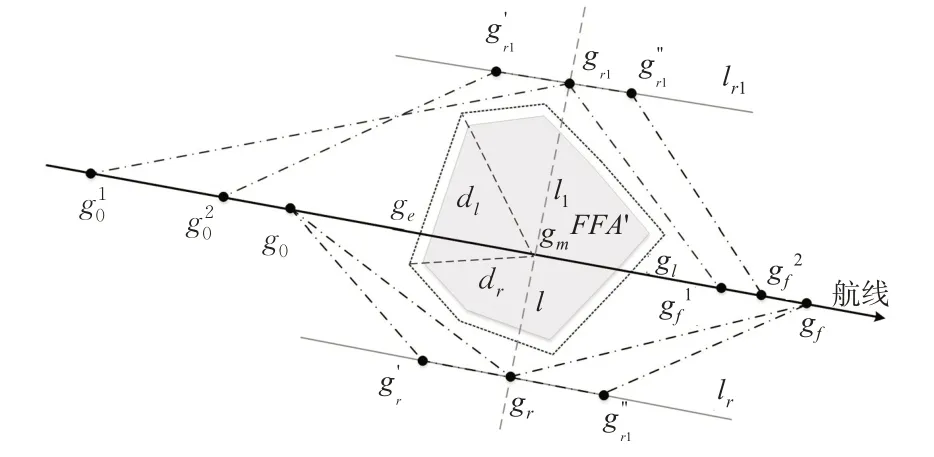
图3 改航点的确定Fig.3 Determination of diverting points

2.2.2 改航约束

1）最大偏航角度限制。最大偏航角度不大于90°。

2）改航路径有效性限制。改航路径与FFA"相交，则改航路径无效。反之，改航路径有效。

3）中间转弯点数量为定值限制。当FFA"被航线一分为二时，有改航路径的一侧或两侧，其对应的中间转弯点数量为3。

4）最小航段距离限制 航空器为完成相应的转弯，飞行距离必须大于3.7 km；若要顺利完成2次转弯，则飞行距离不小于7.4 km，即图3中

5）流量控制固定点的数量限制 流量控制固定点定义为飞行受限区对应的改航始（末）点。数量限制是指FFA"对应流量控制固定点的数值只能为2，3或4，即2≤改航始（末）点的数量≤4。

6）改航路径与FFA"最小侧向间隔限制 改航路径与FFA"保持至少14 km（航路兼最小空中走廊宽度的1/2）的侧向间隔。

其中，最大偏航角度限制和改航路径有效性限制的约束，可通过改航始（末）点的内移、外推修正。

2.3 改航路径优化的数学模型

以多架航空器的改航总路径（L）最短和改航路径对应扇区s管制员工作总负荷最小为目标，建立多目标数学模型，见式（7）～（9）。

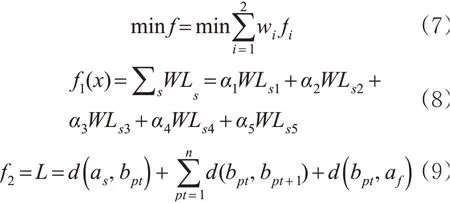
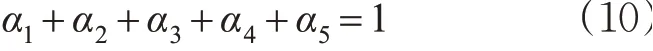
式中：αi(i=1，2，…，5）为各类管制员工作负荷的权重系数。

针对上述数学模型，有如下约束条件。

1）改航时间限制。根据恶劣天气的影响范围，预估改航所需要总时间T。设D sf为航空器对应改航始末点之间的距离；vc为航空器的巡航速度；α为绕飞FFA"所需增加航程的最大百分比。

2）航空器与恶劣天气安全间隔限制。即航空器与恶劣天气的间隔至少大于8 km的最小空中走廊宽度。

3）流量控制固定点的流量限制。流量限制为在满足我国民航区域雷达管制间隔（10 km）的前提下，3 min内过固定点的飞机流≤2架。

4）低复杂度路径优先选择限制。此处的复杂度定义为规划改航路径的航路点数量。数量越少对应复杂度越低，反之，越高。

2.4 改进DPSO算法

本文针对基于几何算法规划的改航路径和原航线中部分固定航段的组合进行优化，该问题属于离散问题，也属于NP问题。因此，借鉴相关文献[18]求解旅行商的DPSO算法的设计思想，重新定义了DPSO算法中状态表示和运算规则。以贵阳区域管制区为例，多航空器改航路径的见图4。

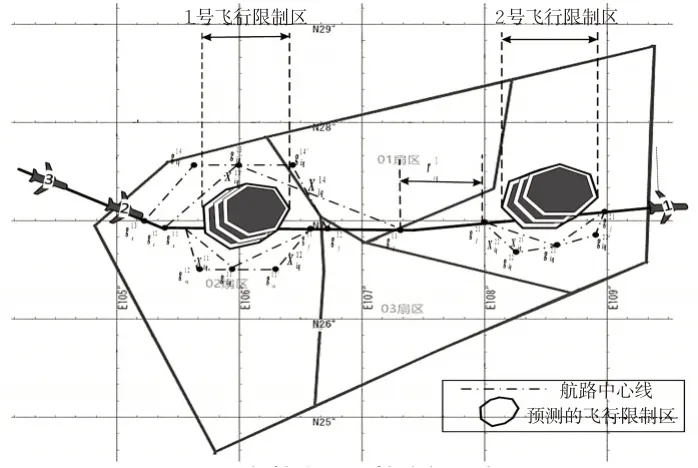
图4 多航空器改航路径示意图Fig.4 Diverting routes of multi aircrafts

2.4.1 运算规则的定义

1）粒子位置的说明。令第i(i=1，2，…，N)个粒子的位置向量为

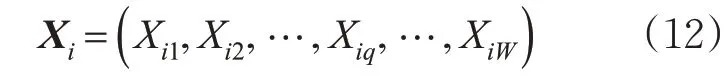
式中：Xi1，Xi2，…，Xiq，…，XiW为W个航班的航班走向。第i个粒子的第q个航班的航班走向的可表示为

2）粒子速度和位置的更新公式。第i个粒子在DPSO算法中速度和位置的向量公式为

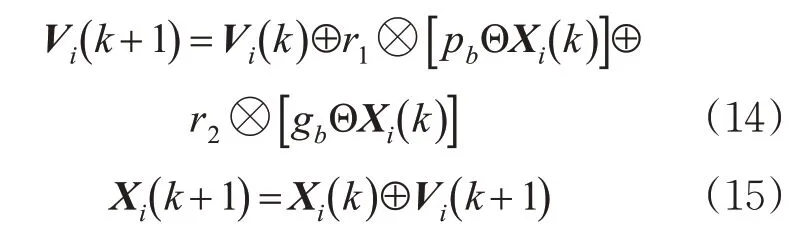
式中：V i为粒子i的速度向量，i=1，2，…，m；k为当前迭代步数；r1，r2为学习因子，取[ ]0,1之间的随机数；pb为粒子i的个体最优位置；g b为粒子i的群体最优位置。

第i个粒子的第q个航班，在第j个飞行受限区中可用改航路径的速度和位置的向量公式，见式（16）～（17）。

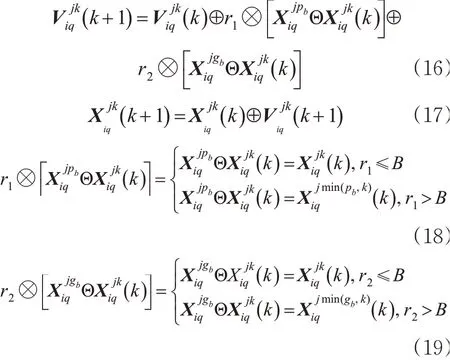
2.4.2 算法的设计

1）确定粒子编码。为简化算法的运算，对改航路径中的关键改航点进行编码，对式（13）中的中间转弯点进行编码，则第i个粒子的第q个航班改航路径编码为以图4中，1号飞行受限区的第i个粒子的第q个航班的编码为例，k的取值为1，2，3和4，其具体编码如下。

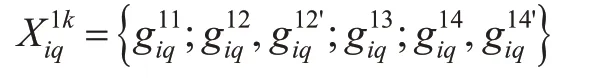
2）确定初始粒子种群。将FFA"下的几何算法规划的改航路径的集合内可随机选择的航班走向作为改进DPSO算法的初始粒子种群。

3）确定适应度函数。令fit(x)=minf。其中，f为改航路径优化的多目标函数。

3 实例仿真分析

我国西南地区为雷暴多发地带，由中国气象数据网（http：//data.cma.cn）可知，2020年7月18日18：00—19日10：00，贵州境内持续有恶劣天气，选取贵州区域管制区作为改航对象。首先，根据中国民航国内航空资料汇编，得到关于贵阳管制区（ZUGY）内航路航线、航路点和扇区等相关信息；其次，结合从贵阳管制单位获得的相关数据，选取受恶劣天气影响的航路（W180，W181，W182，A581和H24）和经过相关航路航段的航空器，进行改航的规划和优化。

其中，经过ZUGY区域并以W180，W181，W182，A581和H24航路为主的航班走向有百余次，参考贵阳管制区2019年高峰日高峰时段的实际运行数据，选取18：30—20：30的飞越、起飞和落地贵阳区域管制区的11个航班走向，45个航班，进行初始建模。

3.1 相关系数的确定

1）参考文献[15]，确定环境模型中FFA"的安全裕度：σmin=5 km，σmax=25 km。

2）参考文献[11]，绕飞FFA"所需增加航程的最大百分比α取20%；

3）确定DPSO算法中的各类参数。参考临时航线的运行特点，固定值B取0.6；迭代次数取100，粒子群种群数取20；使用基于群组AHP与交叉熵的组合赋权法[17]，并进行规范化处理，最终确定的多目标函数权重为：w1=0.584，w2=0.023。

4）TAAM模型中管制员工作负荷的各类负荷权重αi(i=1，2，…，5)取默认设置，依次为0.2，0.1，0.1，0.3，0.3。

3.2 仿真数据分析

参考文献[14]，以像素为单位建立恶劣天气的坐标系，明确恶劣天气的坐标和范围，计算精确度Aa和冗余度Ab。其中，以18：24—18：36（T0，T1）内H24航路恶劣天气的雷达实况为例，预测18：36—18：54即Ti(i=2，3，4)的飞行受限区，则18：24—18：54的飞行受限区见图5。此外，计算得到A a=76.43%，Ab=2.68%。

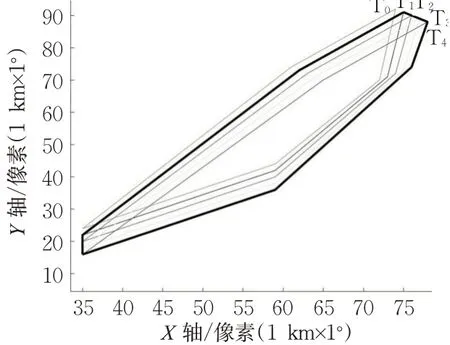
图5 恶劣天气对应的飞行受限区图示Fig.5 Flight-forbidden area corresponding to severe weather

1）构建改航环境。采用Graham算法对零星并且相近的恶劣天气进行凸壳划设，并基于滚动时间窗（天气预报的雷达更新周期为6 min）进行恶劣天气的预测以及合并，得到贵阳区域管制区内的散点状分布的FFA"，见图6（a）。

2）生成改航路径。根据环境模型，考虑实际运行和相关约束，利用几何算法规划多条改航路径，并设置空域规则以贴近实际的航班运行，改航路径在TAAM模型中的情况，见图6（b）。

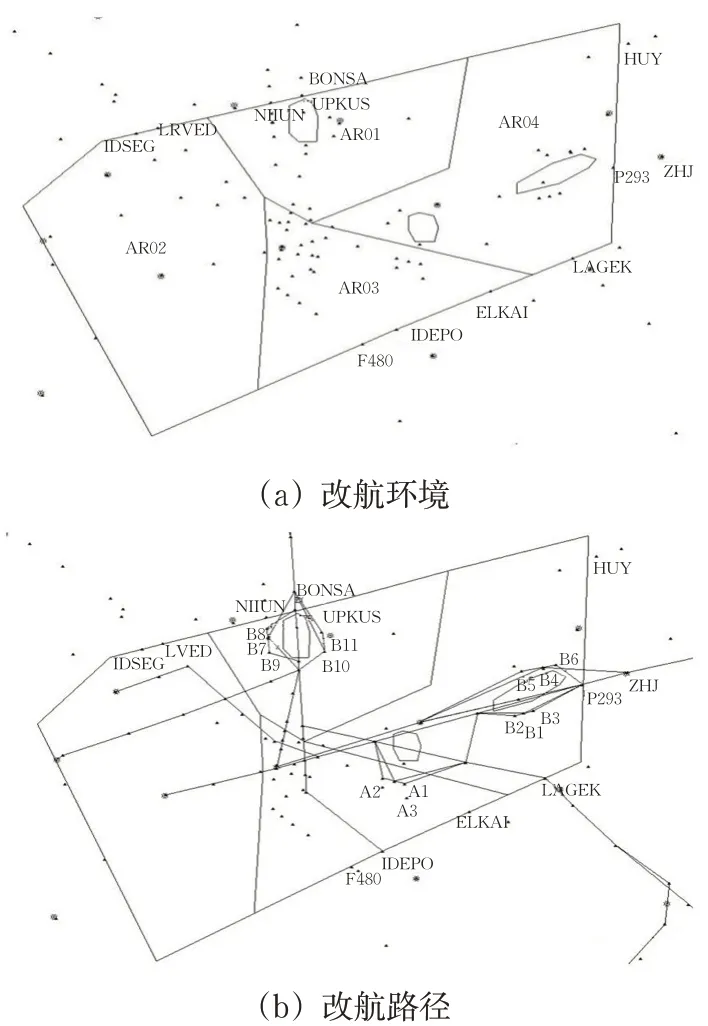
图6 改航环境和改航路径的图示Fig.6 Diagrammatic representation of the redirected environment and diverting routes

3）管制工作负荷和改航路径的汇总。恶劣天气主要影响的是AR01，AR03和AR04扇，改航数据汇总见表1，管制员小时负荷数据见图7。其中Origin代表原始（改航前）方案，PSO代表PSO算法对应的最优方案，DPSO代表改进DPSO算法对应的最优方案。而改航环境下算法适应度的变化见图8，其中改航距离通过规范化处理，量级上与管制员工作负荷基本保持一致，故适应度值的单位取为当量架次。

图7 管制员工作小时负荷图示Fig.7 Graphical representation of workhour load of the controller

表1 改航数据汇总Tab.1 Summary of diverting data

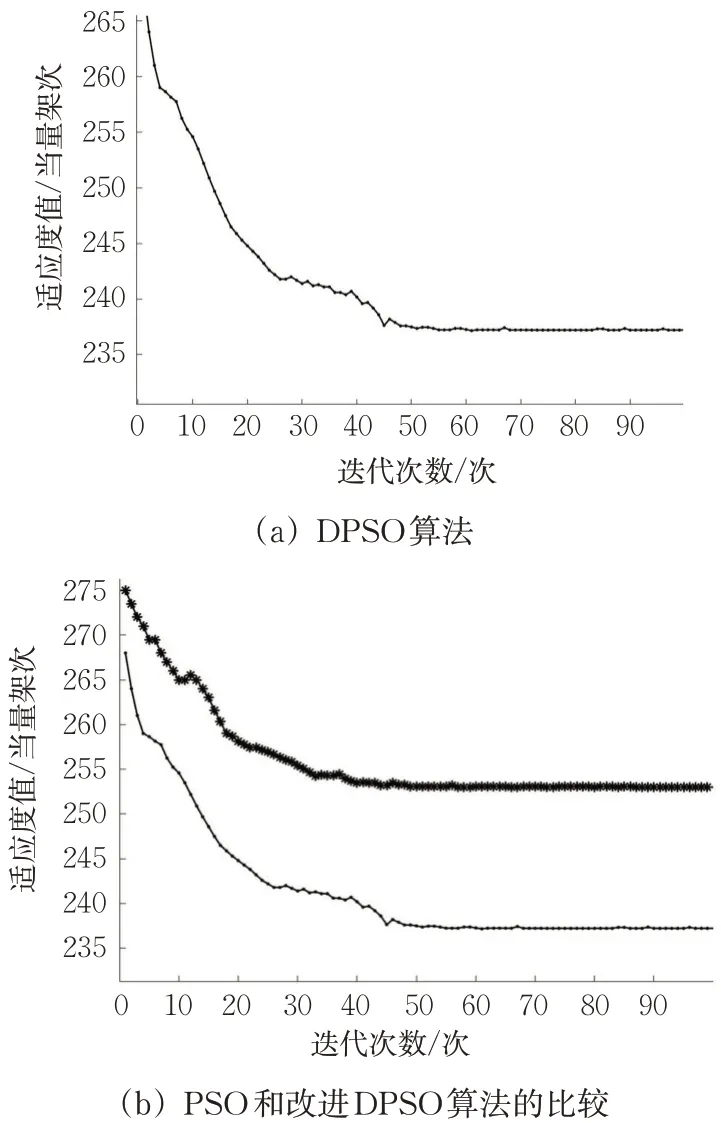
图8 改航环境下算法适应度的变化Fig.8 Variation of algorithm"s adaptation in diversion

由图8可知，迭代50次左右，改进DPSO和PSO算法适应度值均趋于平稳，改进DPSO算法的适应度值更低，并且其最优方案的管制员工作负荷和改航距离较原方案分别增加了9.86%和18.66%，而对比PSO算法最优方案的管制员工作负荷和改航距离则分别降低了7.52%和4.48%，改航效果较贴合实际。以16：48：00从杭州萧山机场起飞，18：54：34落地毕节飞雄机场（贵阳管制区内的小机场）的CDC8823航班数据为例，其机型为A320，巡航速度（地速）为814.88 km/h，具体改航数据见表2。其中A1，A2，A3，B1，B2和B3均为改航点，表中距离为与跑道末端的距离，n mile。

由表2可知，CDC8823航班的改航满足式（11）改航时间限制的约束条件。

3.3 改航算法的对比和验证

为验证恶劣天气下多航空器改航路径的仿真优化算法的有效性、科学性，对比基于恶劣天气的多目标粒子群算法（MOPSO）和非支配排序遗传算法（NSGA-II）的改航路径规划。在2种对比算法中对应构建30×30的栅格环境，每个栅格设置为13 km×13 km[11]，并以ZUGY区域中受恶劣天气影响的H24航路中的航段（P159-ZHJ-P293-XONID-UBDID-MASRO）为例，此航路段长183 n mile（338.916 km），其与FFA"在栅格环境中的情况，见图9（a）。

其一，采用MOPSO算法，设置相关参数[11]；其二，采用NSGA-II算法，设置适当参数[19]，其中种群数取40。2种算法的改航路径结果见图9。

其中，MOPSO算法的改航路径长为350.032 km；NSGA-II算法的改航路径长为347.849 km；以CDC8823航班数据为例，考虑W182航路上的FFA"，在XONID-UBDID有2次改航，采用改进DPSO算法的仿真优化算法的改航路径长为386.698 km（含2次改航增加的34.077 km），而采用PSO算法的仿真优化算法的改航路径长为394.291 km（含2次改航增加的40.188 km）。以A320巡航速度（地速）814.88 km/h为例，上述4种方法均满足偏航角度限制和改航时间限制的约束。

表2 CDC8823航班的改航数据Tab.2 Date of the diversion of Flight CDC8823

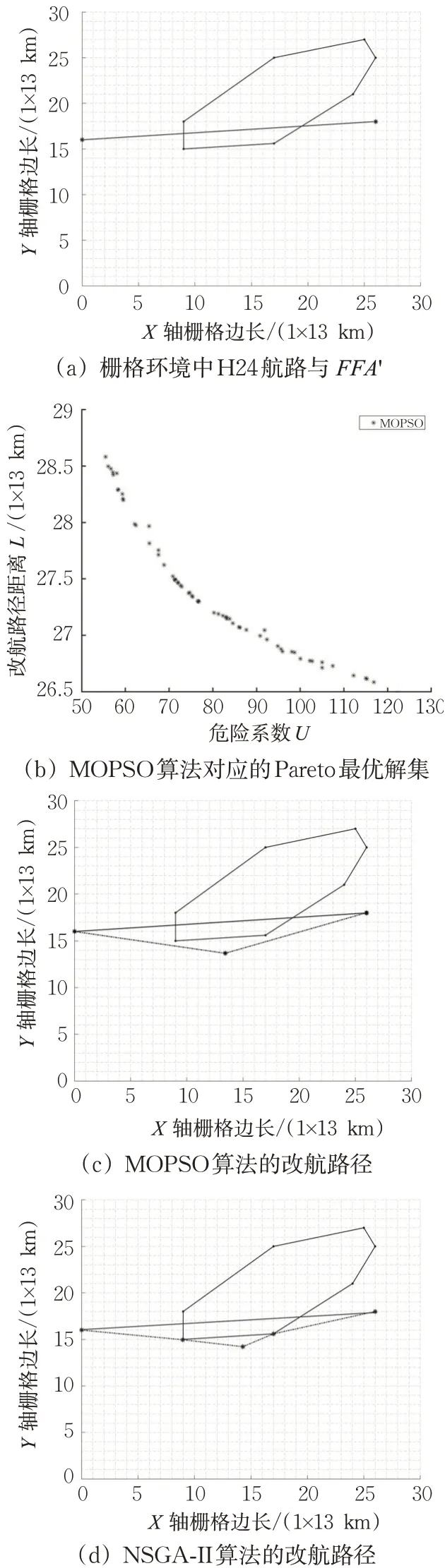
图9 MOPSO算法和NSGA-II算法的改航路径结果Fig.9 Results of the MOPSOalgorithm and the NSGA-II algorithm for diversion

此外，虽然MOPSO算法与NSGA-II算法和本文方法相比，其改航路径距离均略小，但是其算法的运算时间较长，未考虑管制员工作负荷，当出现空中交通拥堵时，可能存在改航路径与其他航班飞行路径的潜在冲突，且在Matlab程序中难以实现管制员的工作模拟和实时仿真。

而本文方法规划了多条改航路径，考虑了管制员工作负荷，利用了改进DPSO算法和TAAM软件的仿真优化算法，可在缩短改航路径距离的同时减少管制员工作负荷，较之其他算法，更加贴近实际管制工作，更具有工程上的可行性。

4 结束语

本篇针对典型区域管制区进行改航规划和优化，从航班安全运行和管制员有效调配的角度出发，结合约束条件，改进DPSO算法中粒子速度和位置的运算规则，使其适合于改航路径的优化与求解，通过Matlab软件和TAAM模型实现算法的多次迭代，快速得到多个航空器的优化改航路径。结果证明，本文研究的仿真优化算法，可达到航班分流，减少管制员工作负荷和缩短改航路径的目的。

未来工作包括优化环境模型，建立更精细的动态环境模型，改进恶劣天气的度量，以便更好地说明哪些天气类型（形状、大小、严重程度）会对改航产生不利影响，以及考虑改航路径的三维建模。