基于时空网络的铁路空车调配动态优化模型*

郑可心 宋 瑞 李光晔

（北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室 北京100044）

0 引 言

铁路货运“实货制”改革[1]以后，对铁路货运服务质量、信息化管理水平等提出了新的要求，向铁路货运实现市场化迈进了关键一步。铁路空车资源的优化配置，有利于降低运输成本、加快车辆周转，是提升铁路货运服务质量和竞争力的一项重要内容。

现阶段关于空车资源优化配置的国内外主要研究可分为静态空车调配、确定性动态空车调配[2-3]和随机空车调配3个方面。相关研究将空车调配问题视为运输问题、车间调度问题、库存问题和多商品网络流问题[4]等，并在此基础上引入了车种代用[5-6]、空重车流协同优化[7]等多个角度的研究。铁路空车调配问题最早的研究均为静态空车调配问题，由于缺乏对时间维度的考虑，研究得到的空车调配策略不够灵活，不能适应铁路实际生产。程学庆[8]用模糊综合评判方法对铁路运输应急物资的优先权进行了计算，结合车种代用构建了考虑应急物资优先权的多目标空车调配模型。陈军华等[9]将企业铁路煤运通道空重车流的协同优化问题视为多重指派问题，建立了企业铁路煤运通道空重车流调配优化模型。薛锋等[10]提出运用D-W分解算法求解静态空车调整模型，并证明了其时间算法复杂度的优越性。确定性动态空车调配问题是指一定的周期内，在空车供需情况确定、路网条件不变的情况下，空车调配决策应随时间推移而变化。Holmberg等[4]研究了瑞典国家铁路的空车调配问题，将空车调配问题视为多商品网络流问题，以满足客户需求和总费用最小为目标，并将通过能力约束、车种代用和列车时刻表等综合考虑设计优化模型。M.F.Gorman等[11]介绍了美国CSX公司开发动态车辆调配优化系统（DCP），系统每隔15 min对管辖的2.1万路网中全部空车进行动态配空，DCP系统每年为公司节省超过5 100万美元，在实际应用中产生巨大的经济效益。王龙等[12]运用时空网络技术，构建全路同构支点路网空车动态调配优化模型，并提出1种基于混沌思想的粒子群算法对大规模路网空车动态调配问题进行求解，还通过模型计算结果设计了路网分界口排空流量测算方法。Jing等[13]提出了1种量子衍生免疫克隆算法求解动态空车调配问题。随机规划理论也被运用到空车调配问题。雷中林等[14]构建了1种特殊的随机机会约束模型来求解铁路空车调配问题，并设计了遗传算法求解模型。邹华鹏[15]采用不确定规划中的机会约束优化理论分别对车流波动和供需波动2种情况下的空车调配问题构建了车流运送的优化模型。综上，空车调配的动态性问题一直是国内外学者研究中关注的重点问题。而我国铁路由于长期沿用计划模式，弱化了空车调配的动态性[16]。在现有空车调整模式下，我国铁路空车调配难以实现全路网动态优化，但是路局公司（以下简称路局）管内的空车调配动态优化问题是值得思考的[17]。通过构建时空网络的方法，将空车调配问题建模为多商品网络流问题，能够直观表达空车调配随时间变化的过程，对我国铁路局管内空车调配动态优化问题具有指导意义。

针对路局管内动态空车调配问题，对既有时空网络构建方法进行改进，将空车调配问题视为多商品网络流问题，并在此基础上引入车种代用的考虑，构建了基于时空网络的铁路空车调配动态优化模型，为路局内部日常空车调配方案提供依据。

1 时空网络的构建

既有采用时空网络技术解决动态空车调配问题的相关研究，将时空网络分为离散型时空网络和连续型时空网络，为了降低网络复杂度，往往选择离散型时空网络的方法，将时空网络中的时段以相等的时间间隔进行划分，取2～3 h为1个时间阶段[18]。但是这种划分方法存在描述问题的精确度不够的缺点，为此笔者对时段划分方法进行了改进，在既有离散型时空网络的基础上，将时空网络中的时间段分为紧张时段、正常时段和空闲时段，以精确描述作业能力的变化，同时降低网络规模。构建路局系统的时空网络见图1。

图1 时空网络的构建Fig.1 Construction of the time-space network

该时空网络以1 d（24 h）为1个周期，并将1 d划分为多个时段，各时段的时长不是固定大小的，而是根据实际路局的到发车情况进行细分。图1中的时间段分为紧张时段、正常时段和空闲时段，例如，时段2为该路局的紧张时段，以1 h进行划分。此外，若某1个时段中不发生空车走行，可以在时空网络中将该时段去除，以减少网络规模。将物理网络中的节点（车站1、车站2、车站3和分界站）根据划分的时段进行拓展得到时空网络节点，图1中A1表示车站1在时段1产生的时空网络节点。为便于表示分界站排空车情况，将分界站设为路局内部虚拟空车需求节点。时空网络中的节点确定后，根据列车编组计划（包括空车编组计划和重空混编列车编组计划）和列车运行图确定时空网络中的弧段。图1中共包括2种网络弧，即配空弧和停留弧。配空弧表示空车在时空网络中的走行，时间由2个部分组成，列车运行时间和车站技术作业时间，例如图1中配空弧（A3，B4）表示在时段3由车站1出发且在时段4到达车站2的空车直达列车。同一车站不同时段的节点之间由停留弧相连，表示空车在车站停留。路局系统的空车时空网络构建完成，表述为G（N，A），N为时空网络中的节点集合（包括虚拟空车需求节点），A为网络弧集合。

2 模型构建

通过构建时空网络，直观描述了空车调配的动态变化过程，每1组具有不同特征的空车（空车类型、去向）代表不同的商品流。一方面，由于铁路空车存在不同车种之间的代用现象，因此不同特征的空车（商品流）不是相互独立的。另一方面，由于路局管内空车调配要优先考虑满足分界口排空任务，因此要将排空与局管内配空分开考虑。故动态空车调配问题中的商品流之间是部分可替代的，即局管内空车调配考虑车种代用问题，而分界口排空只考虑多车种。

针对上述空车调配问题的特点，在建模时做如下考虑：①由于空车调配问题和多商品网络流问题之间存在差异，不能直接套用，为此笔者借鉴运输问题（Transportation Problem,TP）的基本思想，增加空车供需约束，将动态空车调配问题转化为多商品网络流问题；②设置2个整数决策变量，用来分别获取配空方案和分界站排空方案，并且能够直观反映出空车在时空网络中的时空径路和流量分配；③设置0-1辅助变量，用来获取配空方案中的车种代用情况。

2.1 模型假设

为方便描述和简化问题，构建的基于时空网络的铁路空车调配动态优化模型，做出以下假设。

假设1。空车的产生及需求的数量、时间已知或可以预测。

假设2。不考虑因列车运行途中发生故障、车辆检修及装卸作业延误而导致的时间延误。

假设3。不考虑重车运输过程对空车的影响。即对于重空混编列车，配空弧的能力不随重车运输的变化而变化。

2.2 符号说明

1）集合定义。N为时空网络中的节点集合，i，j，s，t∈N；S为时空网络中的空车供给站节点集合,索引为s，s∈S且S⊂N；T为时空网络中的空车需求站节点集合，索引为t，t∈T且T⊂N；K为时空网络中的分界站节点集合，索引为k，k∈K且K⊂N；A为时空网络中的有向弧段集合，包括配空弧和停留弧，(i，j)∈A；W st为空车供给节点与空车需求节点之间的OD对集合，(s，t)∈W st；W sk为空车供给节点与分界站节点之间的OD对集合，(s，k)∈W sk；U为空车种类集合，u∈U；V为货物种类集合，v∈V。

2.3 数学模型

以总费用最小为目标，以供给能力约束、满足需求约束、流量平衡约束、线路通过能力约束和车种代用约束等为约束条件，构建空车调配动态优化模型。模型根据路局的空车供需情况和国铁集团下达的分界口排空计划即可实现空车在时空网络中各条弧段上的流量分配，获得空车调配动态优化方案。

2.3.1 优化目标

路局作为企业，追求目标为效益最大化，在实际生产过程中，空车调配会导致一系列费用的产生和变化。模型以路局空车调配总费用最小化为目标。具体地，将空车调配费用概括为以下3种。

1）空车通过弧段（配空弧和停留弧）产生的费用。空车通过配空弧产生的费用为空车走行费用，空车通过停留弧产生的费用为空车在车站内的单位时间停留费用。

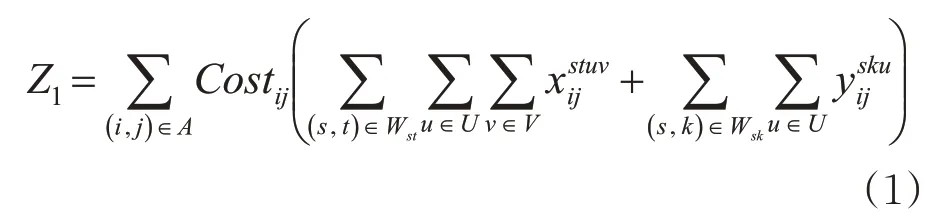
2）空车贮存费用。对于空车供给站，若该站产生的空车在当天没有进行调配，造成空车在该站的闲置而产生的费用，例如空车修护和管理费用。

3）车种代用费用。空车需求站待装的货物由于车种代用而产生的捆绑和加固费用等。

则目标函数为

2.3.2 约束条件

模型的约束条件如下。

1）空车供给站节点供给能力约束。空车供给站节点s发出的分车种空车数应小于等于该节点所能提供的空车数量，即

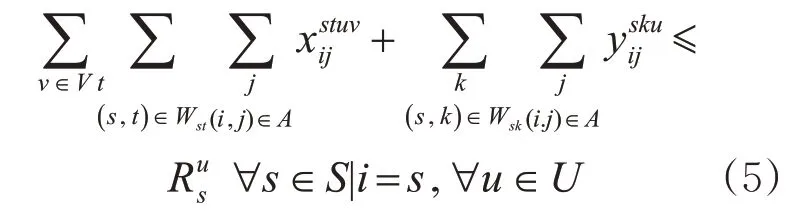
2）空车需求站节点满足需求约束。空车需求站节点t接收的空车数量应满足货物装车需求，即

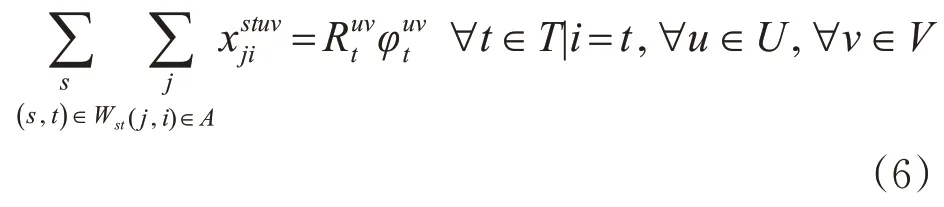
3）满足分界站节点排空约束。分界站节点k接收的分车种空车数量应满足分界口排空计划中的要求，即

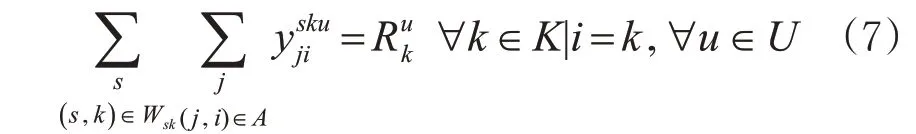
与多商品流问题不同的是，空车调配问题没有直接给出不同OD点对之间运输需求，为了实现空车调配问题向多商品流问题的转化，首先要确定空车在供给站、需求站和分界站之间的点对点调配方案。此时可以将空车调配问题视为传统运输问题中产销不平衡的运输问题，即式（5）～（7）中的供给能力约束和满足需求约束。

4）中间节点流量平衡约束。由于起讫点流平衡约束已包含至式（5）～（7），故本部分只包括中间节点的流平衡约束，对于各中间节点，为保证路径连续，节点的空车流入量和流出量应相等，即

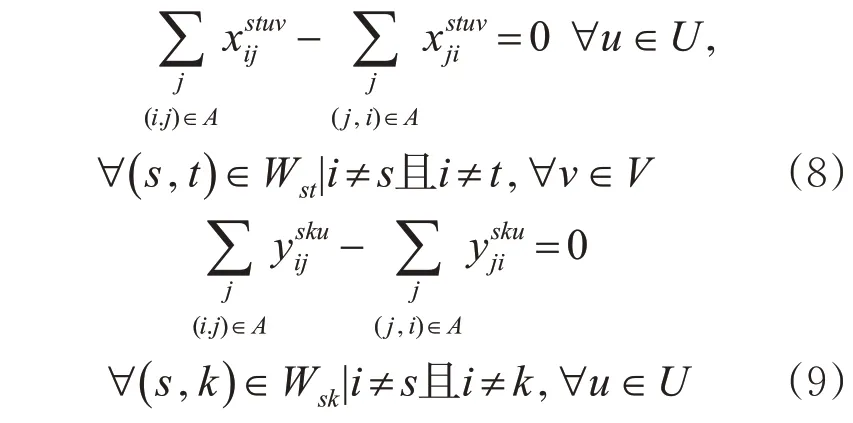
5）线路（配空弧和停留弧）通过能力约束。每条网络弧上的空车流量不得超出其通过能力。对于配空弧，其通过能力为根据列车运行图确定的图定能力，对于停留弧，其通过能力由车站停留能力确定，即

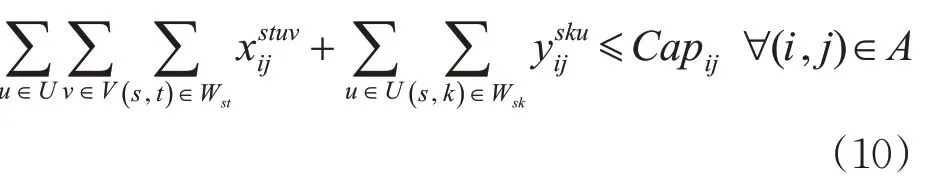
6）车种代用约束。由于考虑路局内的车种代用情况，需求站节点t的分种类货物可以由不同种类的空车运送，但每种货物只能选择1种空车运送，即

该约束仅保证了路局管内排空中不同车种之间的代用，而不影响分界站排空的空车种类。

7）决策变量和辅助变量类型约束

综上，基于时空网络的铁路空车调配动态优化模型见式（4）～（14）。该模型为线性整数规划模型，可以利用商业优化求解器高效求解。

3 算例分析

3.1 算例描述

为了验证动态空车调配优化模型的有效性，选取中国铁路昆明局集团有限公司辖区内铁路货运站配空情况进行分析。为了简化算例复杂度，对区域路网进行归并，将昆明局辖区内的车站按照装车数占路局装车比重进行排序，见表1。

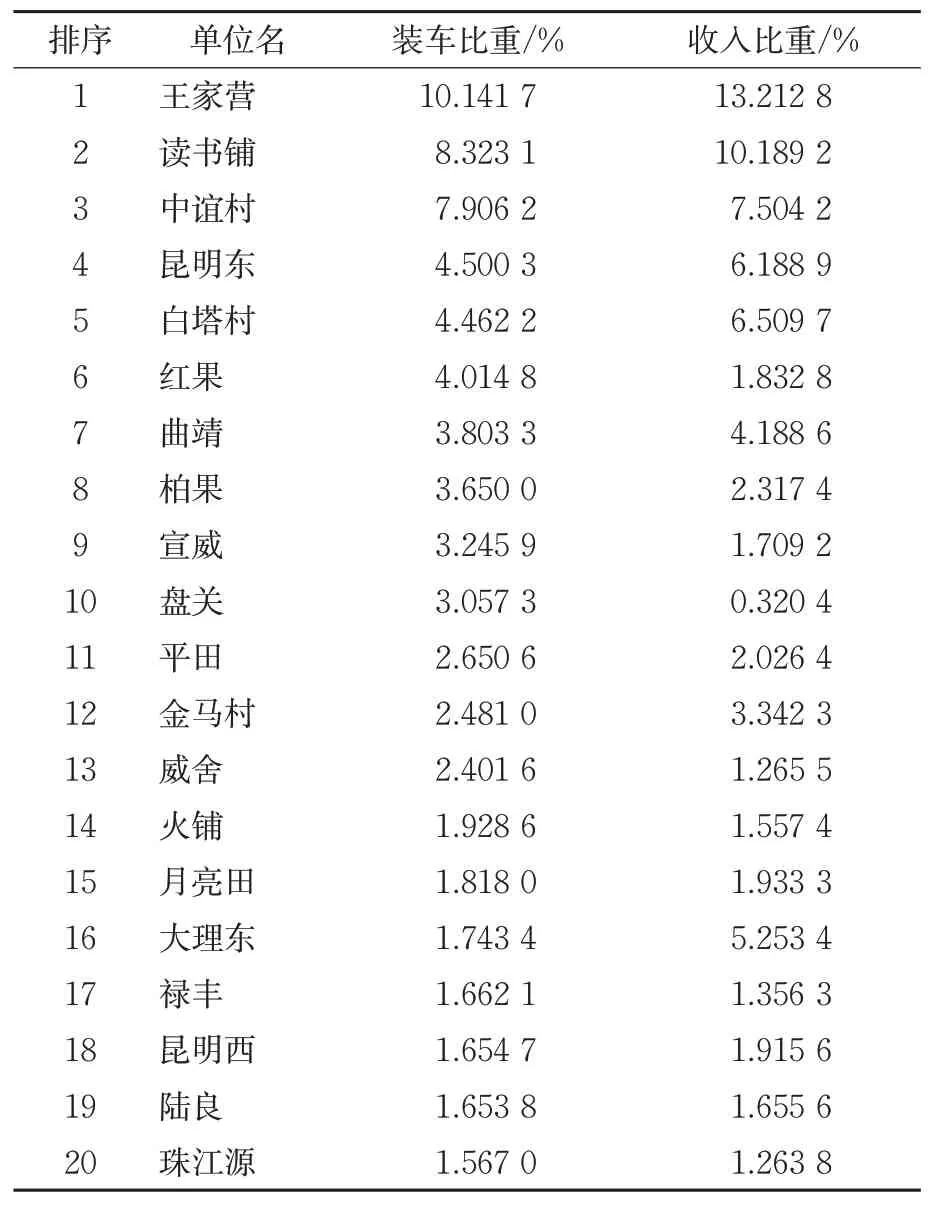
表1 车站装车比重排序表Tab.1 List of loading proportions at stations

选取装车比重大于1且车收入高于路局平均水平的车站，将距离较近的车站也进行归并，得到简化昆明局区域路网见图2。简化路网中共有11个车站，其中有10个技术站和1个分界站，沪昆铁路贵昆段的宣威站为分界站。

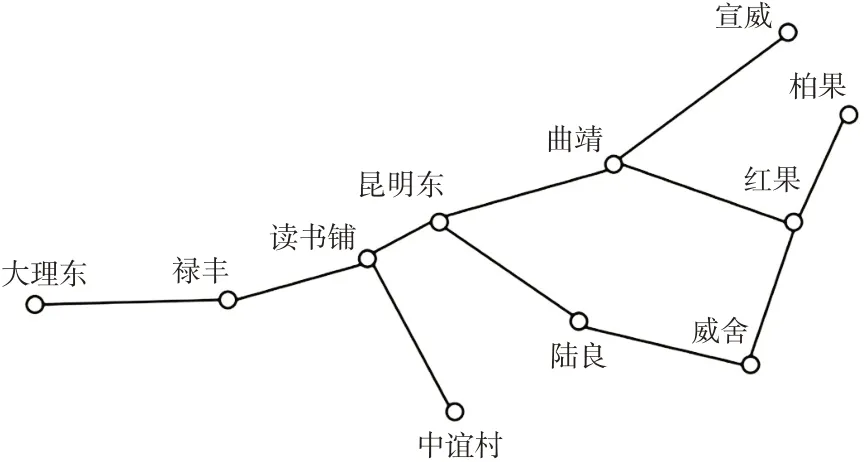
图2 简化路网Fig.2 Simplified road network

表2 和表3是分别为某日空车需求站请求空车数据和空车供给站分车种卸空车情况。

根据表4列车（空车和空重混编列车）编组计划确定时空网络中的配空弧，配空弧的起点和终点分别是列车发站和到站，弧段的时间跨度由列车开行时间和车站作业时间共同组成。

表2 空车需求站请求空车情况Tab.2 Requested conditions of stations demanding for empty cars

表3 空车供给站有效空车数Tab.3 Effective number of empty cars of supply stations

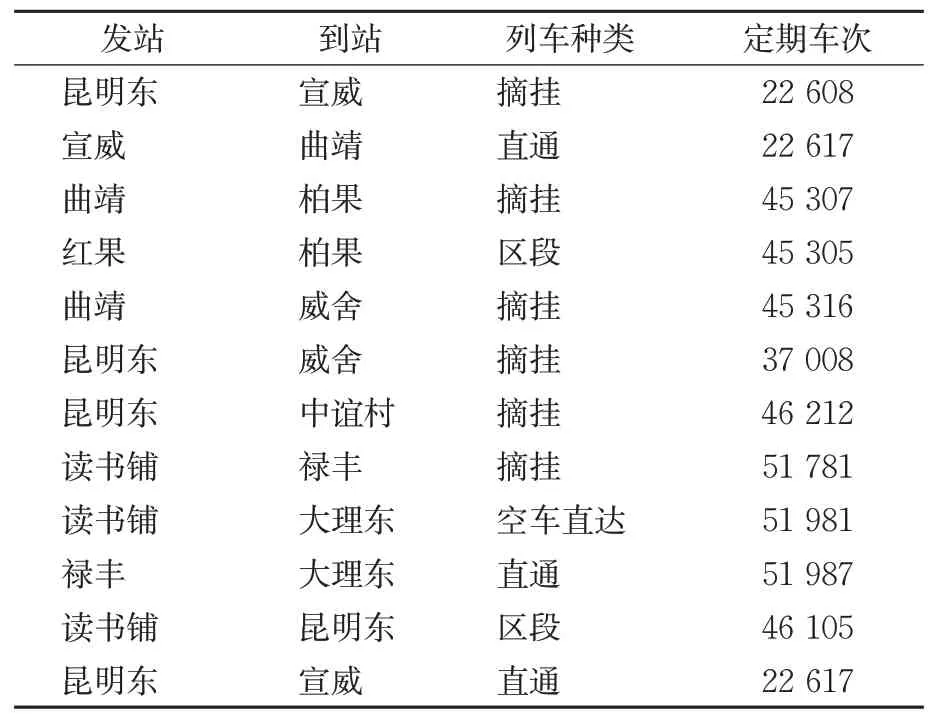
表4 列车编组计划Tab.4 Formation of freight trains

根据上述数据构建包含11个车站的时空网络见图3。模型以1 d（24 h）为1个周期（当日18：00—次日18：00），根据不同作业时段的繁忙程度，将每个时段取1～3 h不等的时长，如时段2时长为1 h，时段9时长为3 h。周期内不产生作业的时段（15：00—18：00）未在图3中显示。

对算例中的费用参数做如下说明：配空弧费用是空车走行成本，根据发站至到站距离和时间计算得来；停留弧费用表示空车在车站的停留成本，停留费用=停留时间×货车费率，为简化计算，假定时空网络中每条停留弧的费用相等；车种代用费用以《全国铁路统计资料汇编2017》中的内容为准，算例中的空车种类有敞车、棚车和罐车这3种，规定敞车可代装粮食；单车库存费用=部属货车库存费×货车周转时间。

3.2 计算结果

图3 时空网络Fig.3 Time-space network

对动态空车调配优化模型进行求解，得到空车调配方案见图4和表5。根据求解结果可知，05：00—08：00，红果向柏果配送罐车20辆；05：00—08：00，红果向威舍配送敞车30辆；20：00—次日02：00，昆明东向陆良配送敞车10辆；20：00—23：00，昆明东向中谊村配送棚车52辆；02：00—10：00，禄丰向大理东配送敞车10辆；20：00—次日02：00，昆明东向宣威配送棚车48辆；05：00—13：00，读书铺向宣威配送棚车12辆。

图4 空车调配方案Fig.4 Solutions of empty-car distribution

表5 模型求解结果Tab.5 Model solutions

3.3 对比分析

3.3.1 与静态空车调配模型对比

为了更直观地说明动态空车调配优化模型优于静态空车调配模型，笔者选取了1种静态优化模型，将算例中的供需情况划分为2个阶段，进行逐阶段优化求解并将成本累计求和，得到静态多阶段优化策略结果见表6。

分析可知，与静态空车调配方法相比，动态空车调配的方法具有以下优势：①动态空车调配优化的总成本为99 560元，相较于静态空车调配优化的总成本有所下降。动态空车调配方法将整个周期内结果最优作为优化目标，得到的优化结果满足整个周期内的空车需求，是整体最优。而静态空车调配方法将1个完整周期划分为不同几个阶段，保证了每个阶段的优化结果为最优，但是整体未必是最优，并且上1个阶段调配过程没有考虑对下1个阶段的影响，使得得到的方案与动态优化方案有所差异。②动态空车调配优化不存在单辆空车无法挂运列车的情况。动态空车调配时空网络中配空弧的构建是依据列车编组计划完成的，对于不超出配空弧能力的空车都能挂运在对应列车上。而静态空车调配在物理网络中进行配空，没有考虑列车编组计划对调配结果的影响。

3.3.2 与既有动态空车调配模型对比

本文提出的空车调配动态优化模型，与既有运用时空网络方法解决动态空车调配问题的模型相比主要存在以下改进：①在时空网络中时间段的划分方式上进行了细分，图3中构建的时空网络将1 d（24 h）共划分成时长为1～3 h不等的时段，且去除了不产生作业的时段，降低了模型求解复杂度。②提出借鉴传统运输问题的模型，将空车调配问题转化为多商品网络流问题，从而使构建的模型不仅可以获取空车调配方案，而且能够直观地看出空车在时空网络中所经过的线路。例如，由图4中的空车调配方案可知，红果站在时段2产生的空车，首先在站内贮存，然后在时段6将20辆罐车调配至柏果站，同时将30辆敞车调配至威舍站，且预计均在时段7到达目的地。在实际生产中，为路局准确把握空车在各个时间的作业状态提供依据。

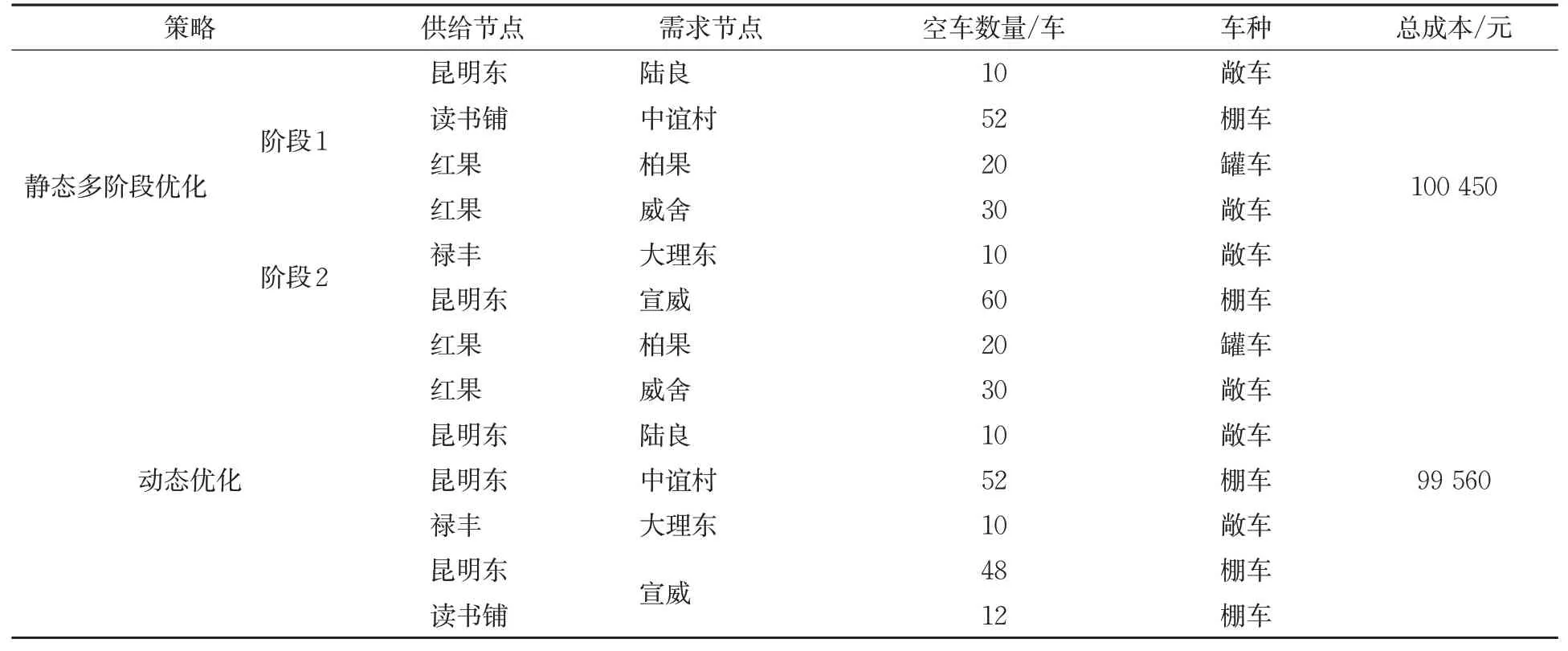
表6 不同策略下调配结果对比Tab.6 Result comparison under different strategies

4 结束语

对铁路局管内空车调配动态优化问题进行了研究。对时空网络中的时间段划分方式进行改进，降低模型求解复杂度。通过改进约束将动态空车调配问题转化为多商品网络流问题，综合考虑空车调配的特点，构建了基于时空网络的铁路空车调配动态优化混合整数规划模型，并利用优化软件求解模型。通过算例分析验证了模型的有效性，对比分析结果表明，相较于静态空车调配模型，本文构建的动态空车调配模型在一定程度上降低了空车调配总成本，且不存在单辆空车无法挂运列车的情况。此外，模型得出的空车调配方案能够更加直观的看出空车在不同时间的作业状态。未来将进一步研究如何将空重车流协同优化和求解全路动态空车调配问题。