基于时间窗的铁路重载运输空车回送优化

段 刚，陈 莉，李引珍，何瑞春

（1.兰州交通大学交通运输学院，甘肃 兰州 730070；2.兰州城市学院数学学院，甘肃 兰州 730070）

1 引言

重载铁路将货源地与消费地连接起来，是大宗货物的运输通道。货源地的装车点分布在与重载铁路相连的集运干支线上，共同构成装车区；卸车点位于线路下游的消费地或转运节点上，共同构成卸车区。货物在装车点装车形成重载列车，通过重载线路运往卸车点；货物在卸车点卸车后形成空车列，再经由相反线路回送到装车点，依次循环，如图1所示［1］。

由于重载运输采用固定车底，实行重去空回的运输组织方法，重车卸空后通过原线路回空到装车点进行装车作业。因此，重载运输空车回送与普通列车空车调运有较大区别，即不需考虑根据某站或某方向需求排空，在空车方向主要是集结空车，单方向组织回送。韩雪松等［2］在分析我国重载运输组合站作业过程的基础上，对组合站组合方案进行优化研究，陈雍君等［3］对列车运行调整计划进行了研究，李鹏等［4］建立了一个重载列车去向模型，并对普通直达列车和重载列车开行方案进行比较，景云等［5］以车辆周转时间最小为目标，对重载铁路集疏运调度系统车流组织进行了优化。范振平［6］对铁路重载运输通道车流吸引区域问题进行了研究，分别提出了纯最短路径法、广义最短路径法和阻尼系数法等三种方法。同时还研究了重载列车的车流组织优化问题，分别构建了三种考虑换重影响的装车地直达优化模型。冯芬玲［7］基于元胞自动机模型建立了铁路重载列车运行组织模拟模型，并对某区间铁路重载运输列车的有关特性和相互之间的关系进行模拟。张进川［8］分析了半封闭式重载铁路空车调整问题的特点，不仅建立了重载铁路卸车端空车回送模型，证明了该问题属于网络最小费用最大流问题［9］，还对重载铁路装车端空车配送进行了优化［10］。

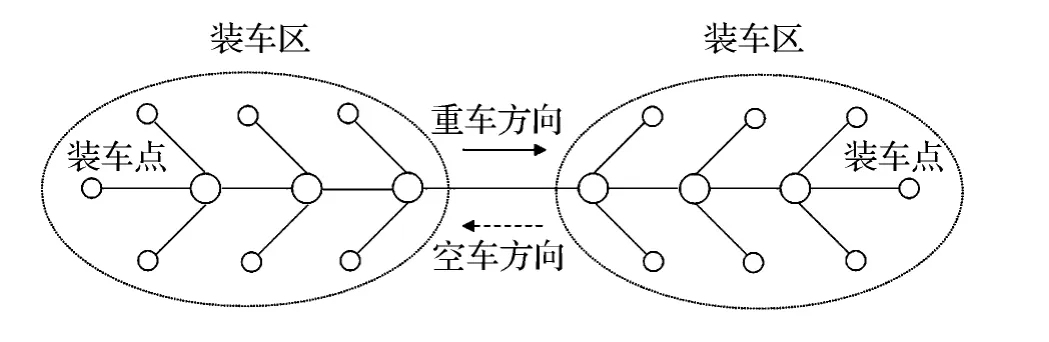
图1 重载铁路集疏运系统示意图

在通过能力允许的情况下，可以将卸车点的空车小列（未经组合的空车列）直接回送到装车点。在不耽误装车点装车的前提下，在组合站对一些重载列车进行组合形成空车大列，然后再在分解站进行分解，最后再运往目的站，这样可以提高线路通过能力和降低运营成本。因此，选择哪些空车列进行组合、以何种方式进行组合，必须制定科学合理的方案，才能做到及时快速的回送空车。本文对重载铁路从卸车区到装车区的整个空车回送过程进行研究，在卸车区通过能力和装车点时间窗要求下，对卸车点运送到组合站的空车列进行组合优化，以求最大限度的满足各装车点对空车列时间和数量上的需求。

2 空车回送优化模型

2.1 假设条件与符号说明

本文遵循以下假设：

（1）各类型空车的供应量大于需求量。实际上，当某类型空车供应不足时，本文可以通过增加一个虚设的空车供应站，不足部分由该虚设的供应站负责供应，将其转化为供大于求的空车调运问题。

（2）卸车点与装车点之间的线路是确定的。

（3）当受到通过能力限制时，要求空车小列在组合站组合形成空车大列，空车大列在到达分解站时必须分解为小列后再运往装车点，即组合与分解必须成对出现。

（4）不同类型空车不能进行组合，只有同类型空车可以组合，由于大秦线目前主要开行单元万t、组合万t及组合2万t列车，所以我们选择下列组合方式：2列5000t空车组合成1列万t组合列车、4列5000t空车组合成1列2万t组合列车、2列单元万t重载空车组合成1列2万t组合列车。

（5）组合站位于卸车区，每个组合站对应若干个卸车点，当卸车点的空车列需要组合时，只在该卸车点所属组合站进行组合。

（6）分解站位于装车区，且只有一个。

参数设置：I— 卸车点（空车供应站）集合；J— 装车点（空车需求站）集合；D— 组合站集合；K— 空车类型集合，K＝｛1，2｝，分别表示5000t重载列车与单元万t重载列车；H— 组合方式集合，H＝｛2，4｝，分别表示2列同类型空车列进行组合和4列同类型空车列进行组合；— 卸车点i卸空后的k型空车列数量，i∈I，k∈K— 装车点j需要的k型空车列数量，j∈J，k∈K；αkh—k型空车列以h方式进行组合的列数，k∈K，h∈H，αkh∈ ｛2，4｝，且规定α12＝2，α14＝4，α22＝2，分别表示2列5000t重载空车组合、4列5000t空车组合成、2列单元万t重载空车组合；Cid— 卸车点i到其经过的第一个组合站d的线路最大通过能力，i∈I，d∈D；Cd，d＋1— 两个相邻组合站d和d＋1间的线路最大通过能力，装车点j所需k型空车到达的时间窗组合站d以h方式组合k型空车列的时间，d∈D，k∈K，h∈H；tkh— 分解站将h方式组合的k型空车列进行分解的时间，k∈K，h∈H；—k型空车列从卸车点i出发的时间，i∈I，k∈K；tij—卸车点i到装车点j的走行时间，i∈I，j∈J；δid∈｛0，1｝，卸车点与第一组合站关联系数，当卸车点i所经过的第一组合站为d时取值1，否则为0，i∈I，d∈D；—卸车点i发出的k型空车小列到达装车点j的时间，i∈I，j∈J，k∈K；— 卸车点i发出的以h方式组合的k型空车大列在分解站经分解后到达装车点j的时间，i∈I，j∈J，k∈K，h∈H。

变量设置：＝卸车点i发往途径第一个组合站d的k型空车列数，i∈I，k∈K，d∈D；＝卸车点i的k型空车小列发往装车点j的列数，i∈I，j∈J，k∈K；＝卸车点i以h方式组合的k型空车列在分解站分解后发往装车点j的列数，i∈I，j∈J，k∈K，h∈H；＝ 通过相邻两个组合站d和d＋1间的k型空车列数，k∈K，d∈D；∈｛0，1｝，当卸车点i的k型空车列其所属组合站d以h方式进行组合时＝1，否则为0，i∈I，d∈D，k∈K，h∈H。

2.2 约束条件

2.2.1 卸车端需满足的约束条件

（1）空车列供应约束

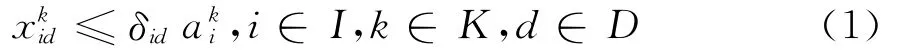
式（1）表示卸车点发出的空车列数量不应超过该站空车列的最大供应量；

（2）空车列组合约束

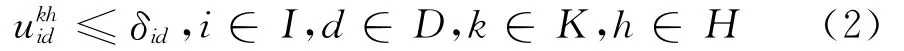
式（2）表示每个卸车点每种类型的空车只能在其所属的组合站进行组合；

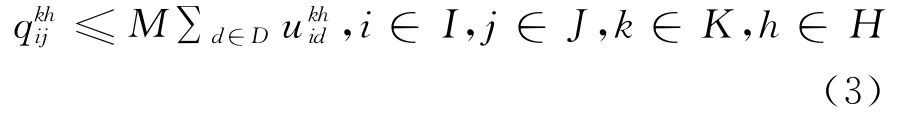
式（3）表示组合列车数量与组合类型的关系，其中M为非常大的正数；

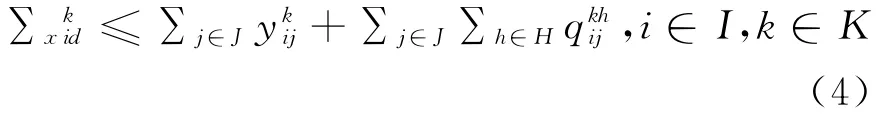
式（4）表示每个卸车点发出的各类型空车通过空车小列和组合列车的方式回送到各装车点；

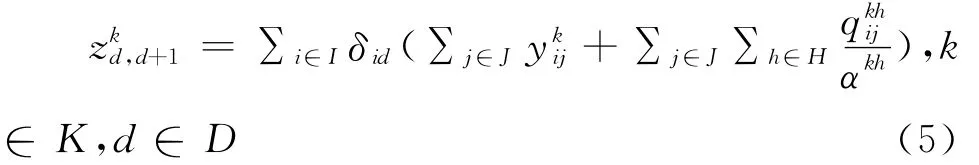
式（5）表示组合站间发送的全部空车列数（包括空车小列和大列）；

（3）线路通过能力约束

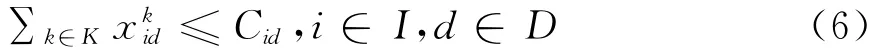
式（6）表示卸车点与组合站间的通过能力约束；

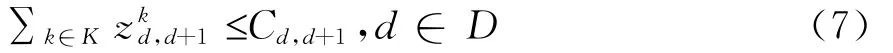
式（7）表示相邻组合站间的通过能力约束；

2.2.2 装车端需满足的约束条件

（4）分解站空车列约束

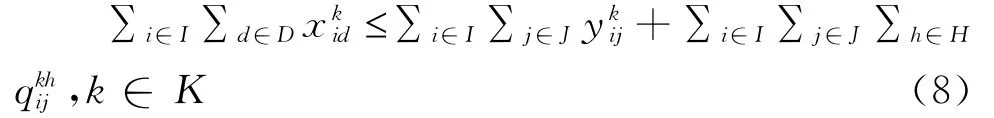
式（8）表示到达分解站的空车列和从分解站发出的空车列应相等

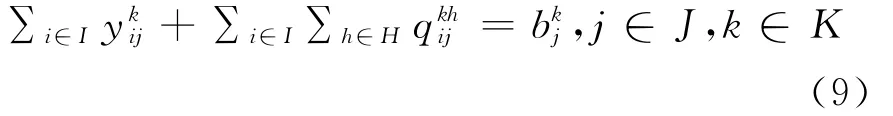
式（9）表示从分解站发往各装车点的空车列可由二种形式组成：空车小列、组合后又被分解的空车大列；

（5）空车列到达时间

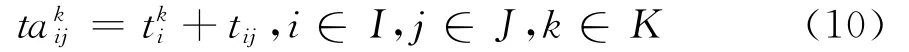
式（10）表示空车小列到达装车点的时间；

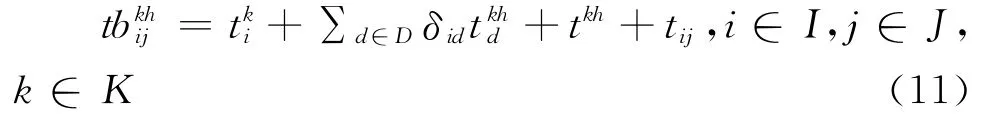
式（11）表示空车小列经组合形成空车大列再被分解为小列后到达装车点的时间；

（6）变量约束

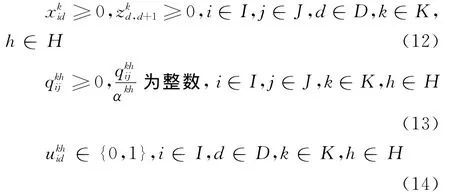
2.3 目标函数

每个装车点对装车时间有一定的要求，空车列过早或过晚到达都会产生不利影响：过早到达会占用到发线，影响车站其它作业，过晚到达则会延误装车。因此，空车回送的到达时间只有在装车点要求的时间段内最理想，本文将其称之为时间窗。但受各种条件的限制，很难达到最理想的情况，所以，本文考虑软时间窗，以空车早到时间或延误时间与空车数乘积之和最小为目标。

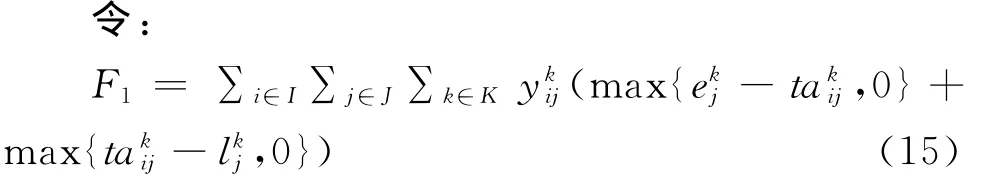
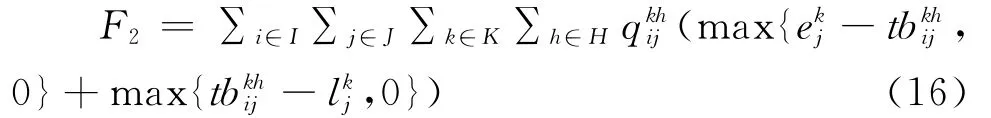
式（16）表示空车大列早到或延误车小时；

所以，目标函数为总的早到或延误车小时最小：

3 算例分析

本文以大秦线为例进行验证。大秦线集疏运系统如图2所示，其中，茶坞站以东为卸车区，湖东站以西为装车区。在卸车区，每个卸车点都有一个组合站与之对应，该卸车点将空车列运往对应的组合站，并根据需要进行空车列的组合。每个卸车点产生的空车数量及类型、空车始发时间、所属组合站、卸车点与所属组合站间的通过能力如表1所示。在装车区，共有17个装车点，每个装车点所需的空车数量、类型以及到达时间窗如表2所示。卸车点到装车点的平均图定时间以及组合站空车列各种组合方式的组合时间分别见表3和表4。相邻组合站间线路通过能力都是104列。湖东站是分解站，所有经组合的空车大列都要在该站进行分解作业，然后再运往装车点。湖东站分解不同类型组合列车时间如表5所示。且在式（3）中，取M＝10000。

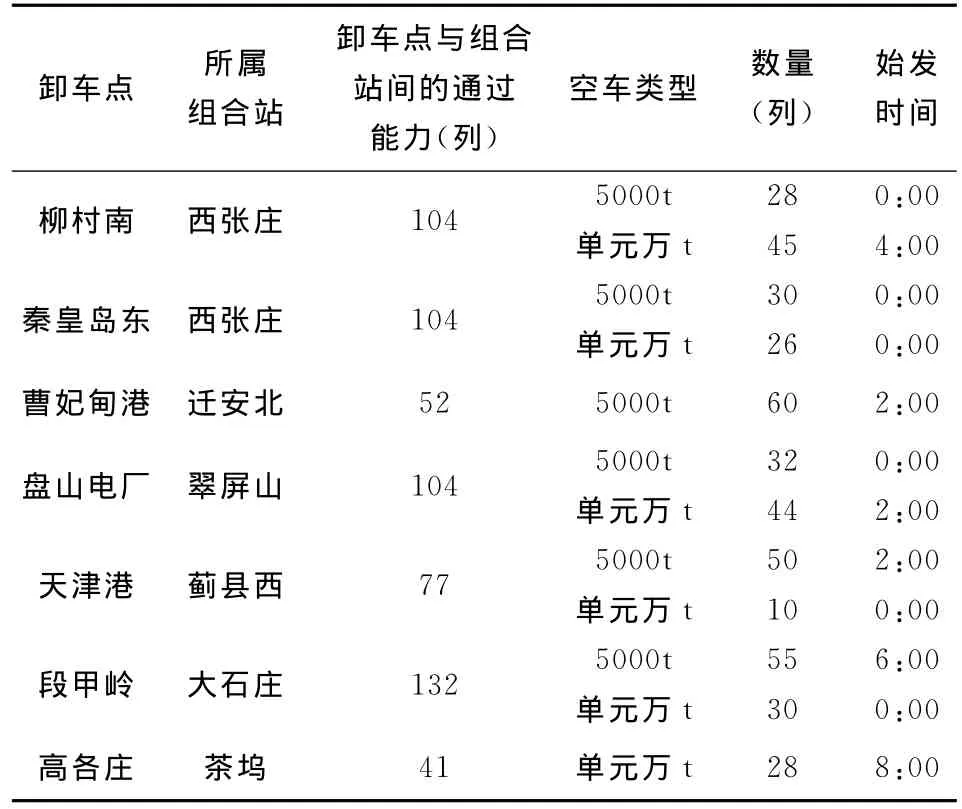
表1 卸车点空车供应信息

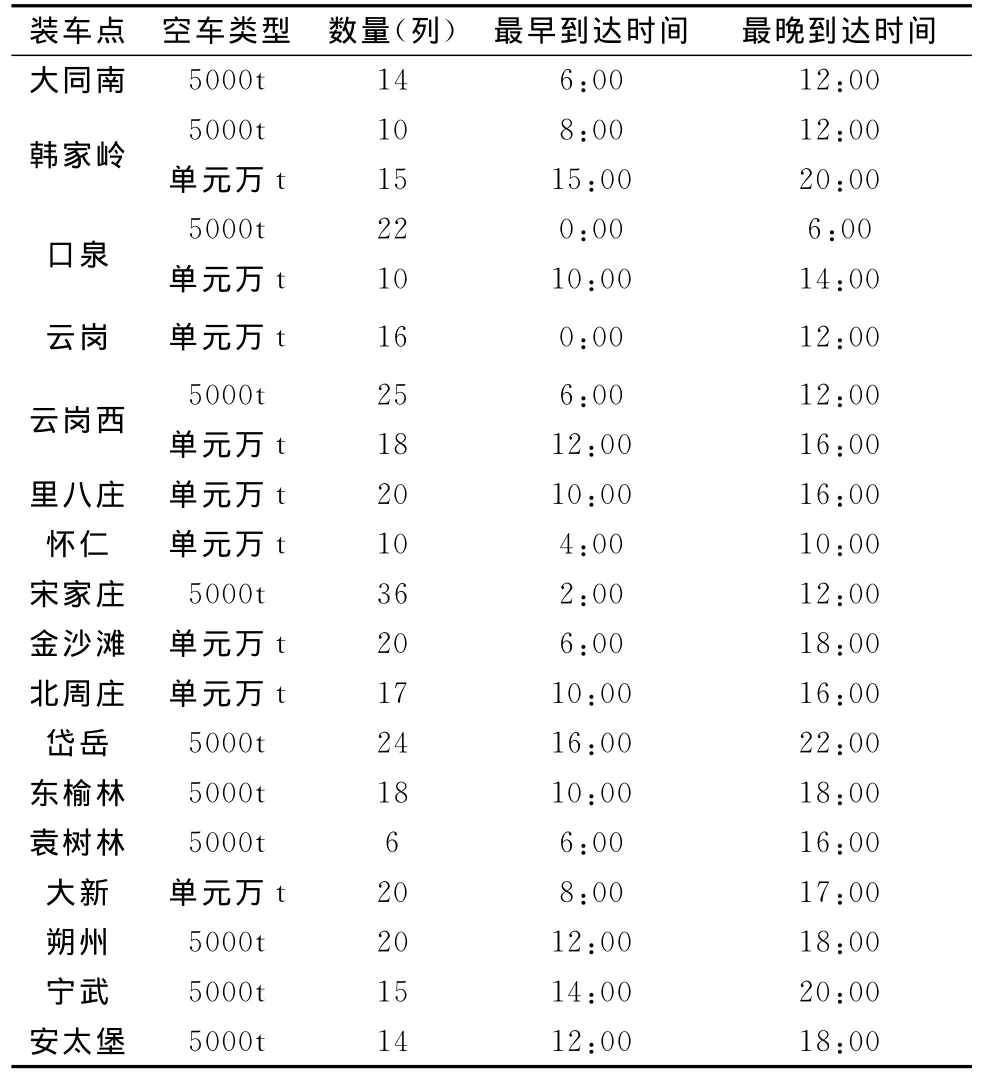
表2 装车点空车需求信息

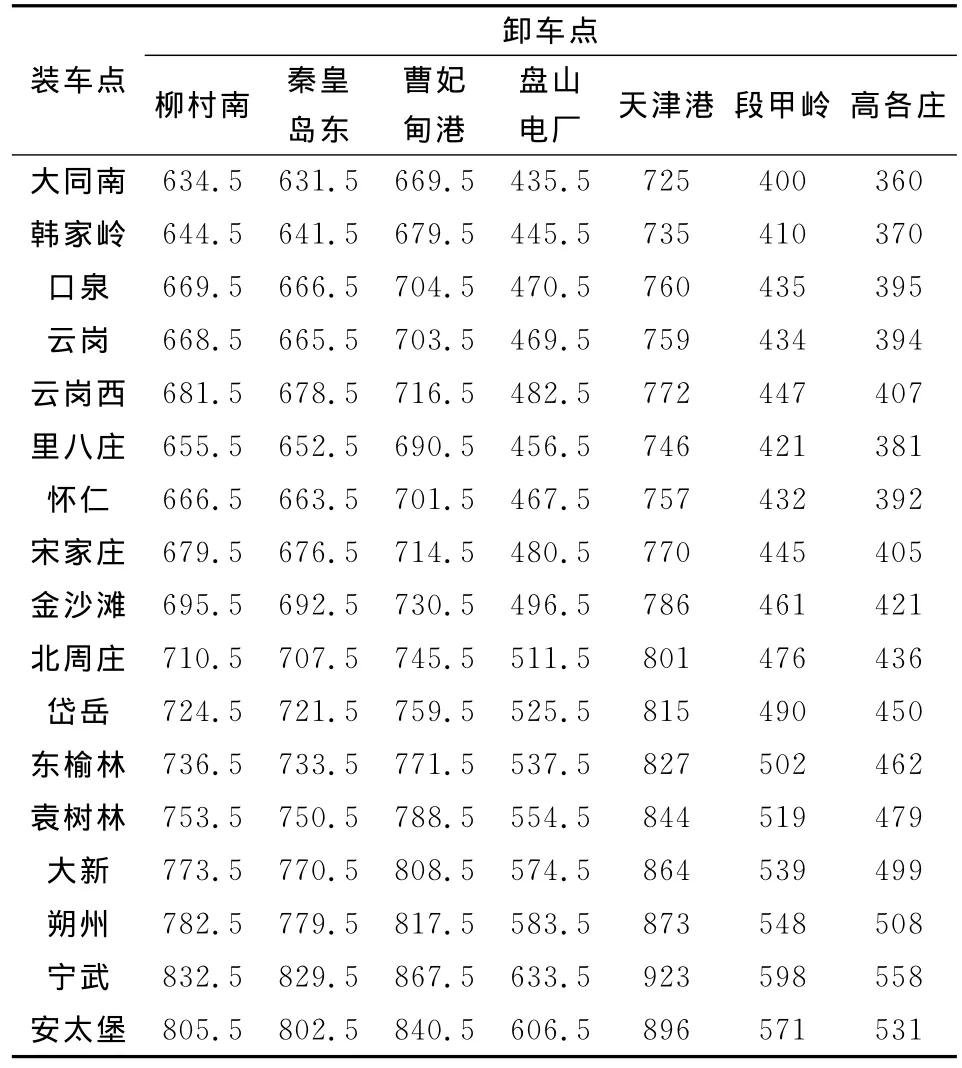
表3 卸车点与装车点间的走行平均图定时间（单位：min）

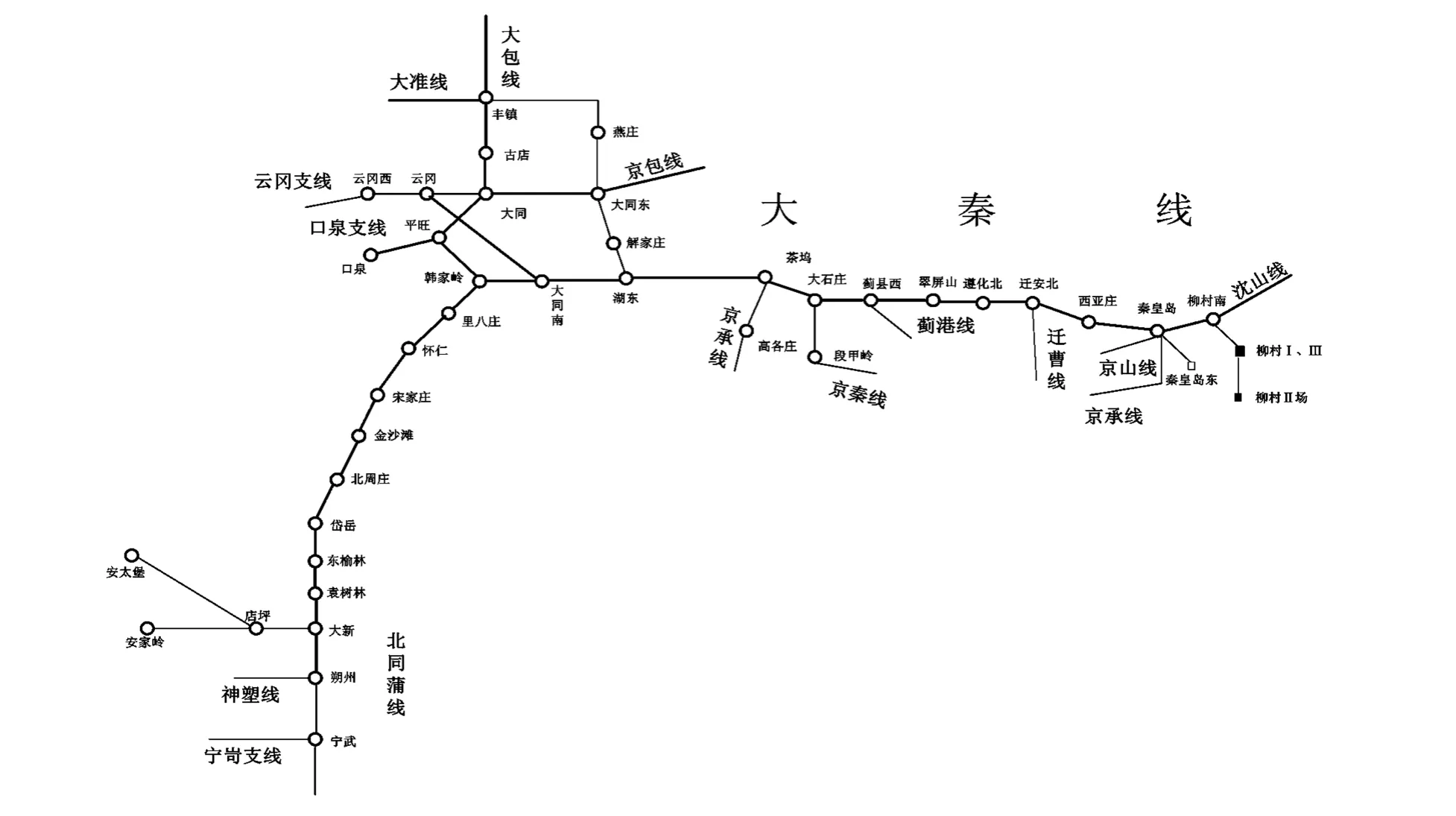
图2 大秦线集疏运线路示意图

表4 组合站空车列组合时间（单位：min）

表5 湖东站组合空车列分解时间（单位：min）

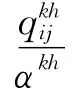
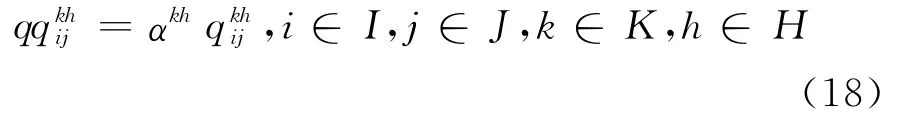
只需令≥0并取整数，即可得到符合要求的。

程序运行2s后即可得到空车最优回送方案，如表6所示。目标值为52.61车小时，其中早到0.26车小时，晚到52.35车小时。

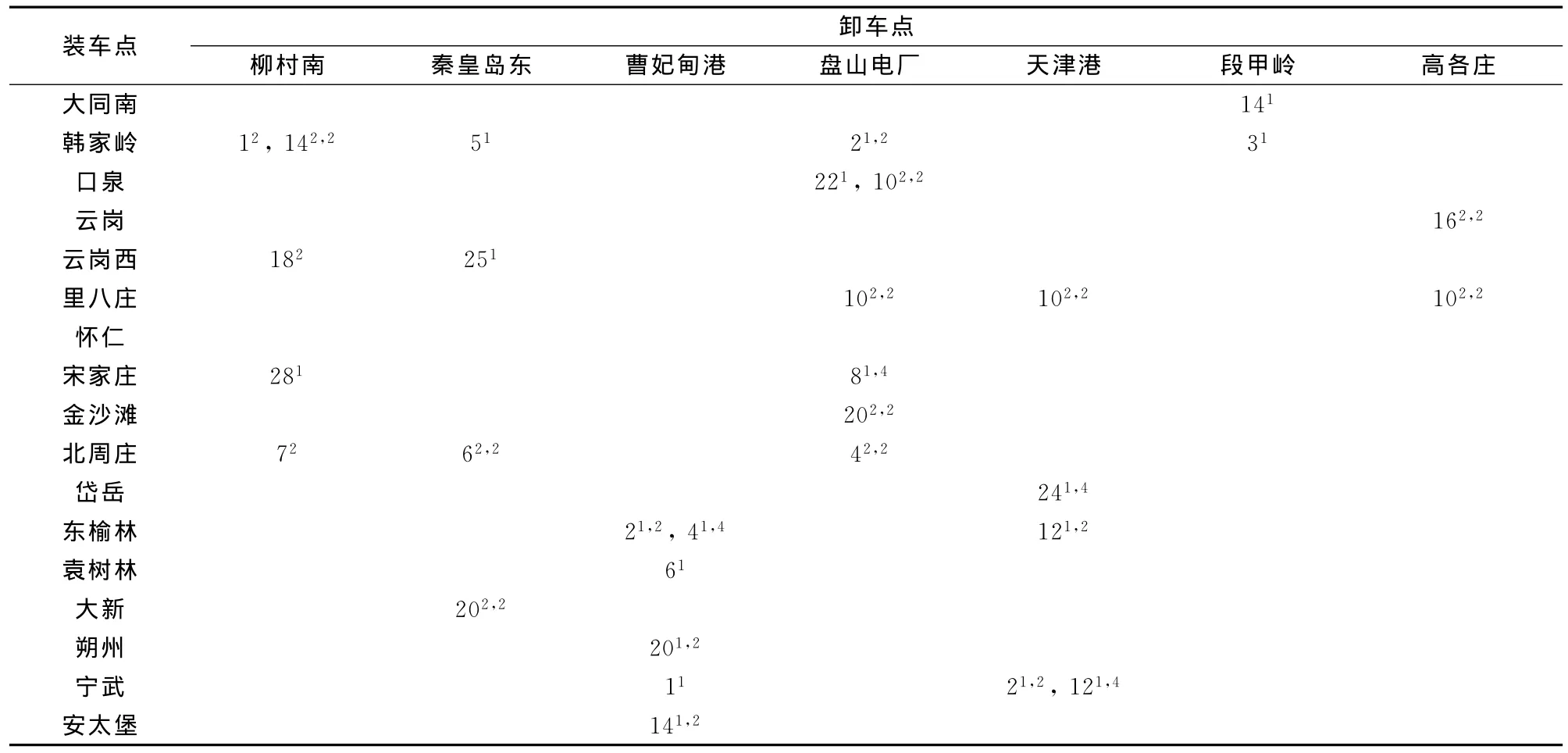
表6 空车回送最优方案

在最优回送方案中，2列5000t列车组合方案为：曹妃甸港分别向东榆林、朔州和安太堡回送了1列、10列和7列空车大列，盘山电厂向韩家岭回送了1列空车大列，天津港分别向东榆林和宁武回送了6列和1列空车大列，共回送了26列空车大列；4列5000t列车组合方案为：曹妃甸港向东榆林回送了1列空车大列，盘山电厂向宋家庄回送了2列空车大列，天津港分别向岱岳和宁武回送了6列和3列空车大列，共回送了12列空车大列；2列单元万t列车组合方案为：柳村南向韩家岭回送了7列空车大列，秦皇岛向大新回送了10列空车大列，盘山电厂分别向口泉、里八庄、金沙滩和北周庄回送了5列、5列、10列和2列空车大列，天津港向里八庄回送了5列空车大列，高各庄分别向云岗和里八庄回送了8列和5列空车大列，共回送了57列空车大列。其中，以组合列车方式回送的5000t列车小列数量（100列）占全部5000t回送空车数（204列）的49%，以组合列车方式回送的单元万t列车数量（104列）占全部单元万t回送空车数（146列）的71.23%。

由于组织合理，全部组合列车都没有早到或延误情况发生。空车小列共发生一次早到情况，柳村南向韩家岭回送的单元万t列车（共1列）早到0.26小时；延误则发生了三次，分别是盘山电厂向口泉回送的5000t列车（共22列）延误了1.84小时，段甲岭向大同南回送的5000t列车（共14列）延误了0.67小时，段甲岭向韩家岭回送的5000t列车（共3列）延误了0.83小时。其中，延误最多的是盘山电厂向口泉回送的5000t空车小列，共计40.48车小时，占全部晚到车小时的77.33%。主要原因是口泉所需5000t列车的时间窗要求较早（在0至6点之间），而与其最近的盘山电厂的走行时间也要7.84h。早到情况则正好相反，韩家岭所需万t列车的时间窗较晚（15至20点间），柳村南发车时间为4点，走行时间为10.74h，所以早到了0.26h。

组合站间的空车回送情况如图3所示。由于西张庄同时为秦皇岛东和柳村南的组合站，因此通过组合站西张庄和迁安北间的列车数较多，共有124列，而两站之间的通过能力只有104列，所以有40列单元万t列车进行了组合，回送的列车数量（空车小列和大列）之和刚好等于线路的通过能力。而其余组合站间回送的空车数由于小于其通过能力，所以组合列车数量主要取决于装车点的时间窗要求。

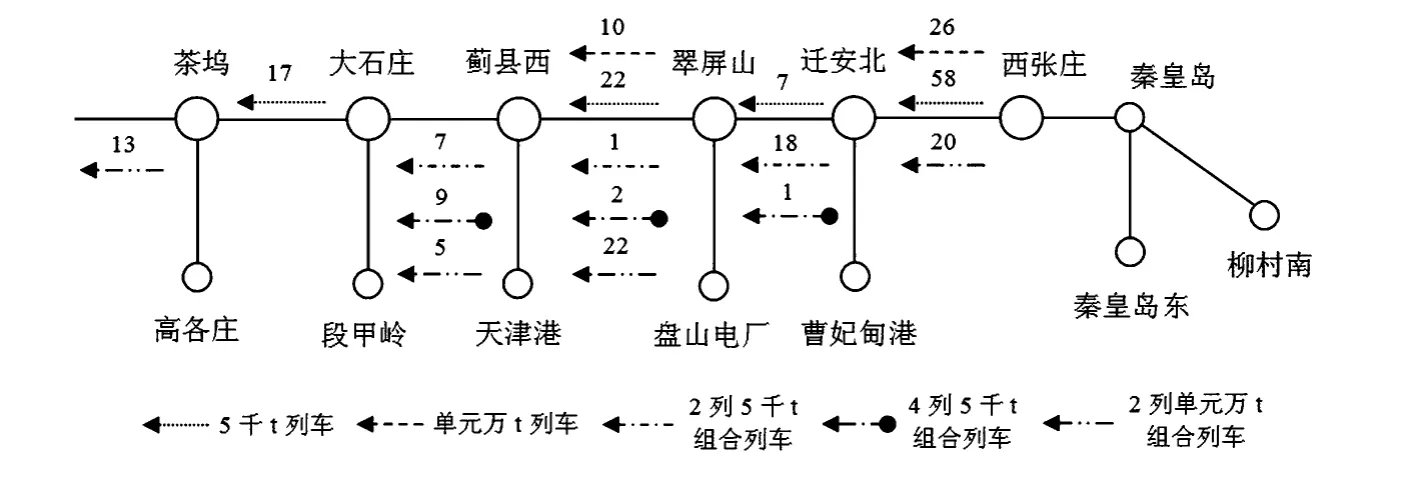
图3 组合站间空车回送示意图

4 结语

作为现代化货运方式的重载运输，在大宗货物的运输上显示出巨大的优势。空车调整是铁路技术计划的重要内容，旨在保证装车的连续性和稳定性。为提高重载铁路空车回送的效率和效益，我们分析了重载铁路运输特点，将其划分为装车区和卸车区两部分，综合考虑线路通过能力、装车点时间窗要求、列车组合方式以及降低运营成本等因素，建立了从卸车点到装车点的重载运输空车回送全程优化模型，通过大秦线的实际数据验证了模型的正确性和有效性。为简化模型，本文没有考虑列车追踪间隔时间这一因素，也就是空车回送时线路被占用的先后顺序，我们将在后续的研究中对此进行研究。

［1］赵鹏，张进川，唐宝刚.基于组合列车的重载铁路装车区车流

组织优化模型研究［J］.中国铁道科学，2010，31（6）：116－121.

［2］韩雪松，郭洪洋，彭其渊.铁路重载运输组合站重载列车组合方案的优化方法［J］.铁道学报，2012，34（12）：1－7.

［3］陈雍君，周磊山，余吉安.重载铁路列车运行调整计划的序优化策略研究［J］.铁道学报，2013，35（1）：1－7.

［4］李鹏，吴小强，林柏梁.基于遗传算法的重载与非重载去向开行方案比较研究［J］.中国铁道科学，2000，21（3）：38－43.

［5］景云，何世伟，郝东红.重载铁路集疏运调度系统空重车流协同优化研究［J］.交通运输系统工程与信息，2012，12（5）：123－129.

［6］范振平.重载铁路通道车流吸引区域及始发直达重载化研究［D］.北京：北京交通大学，2008.

［7］冯芬玲.铁路重载运输发展动因及组织策略研究［D］.长沙：中南大学，2009.

［8］张进川.半封闭式重载铁路运输组织关键技术研究［D］.北京：北京交通大学，2008.

［9］张进川，杨浩，魏玉光.重载铁路卸车端空车回送模型研究［J］.交通运输系统工程与信息，2008，8（4）：96－102.

［10］张进川，杨浩，魏玉光.重载铁路装车端空车配送模型［J］.中国铁道科学，2009，30（4）：113－117.