多阶段空车调整方法在车流推算系统中的应用研究

单 武

（国家铁路局 信息中心，北京 100891）

多阶段空车调整方法在车流推算系统中的应用研究

单 武

（国家铁路局 信息中心，北京 100891）

本文所研究的空车调整模型属于铁路运输信息集成平台下的车流推算系统。车流推算模型能够比较准确地给出在多阶段路网中车站空车的需求量和提供量。针对铁路网络空车调整问题的动态变化特性，建立了多阶段动态空车调整模型，模型的目标函数考虑了与时间因素相关的空车滞留费用和需求未满足惩罚费用等相关费用，设计了模拟退火的启发式算法并进行了求解。对一个简单的路网进行了验证，结果表明，该模型及算法能够较好地解决动态变化环境下的空车调整问题。

铁路运输；多阶段空车调整；时空服务网络；铁路路网；模拟退火算法；车流推算系统

由于铁路货物运输供需关系的不平衡性，导致铁路网（简称：路网）中有些车站的装车大于卸车，而有些车站的卸车大于装车。卸车大于装车的车站会产生多余的空车，而装车大于卸车的车站则需要空车，为了平衡运输资源，加快货源的流通，充分利用路网，需要将多余的空车调配到需要空车的车站。

空车调整是车流推算中一个相对复杂的问题，国内外很多的学者对其进行了深入的研究。文献[1]考虑了能力约束条件下的空车调配问题，建立了空车调配数学模型，并设计分步优化迭代算法进行求解。文献[2]考虑了滞留费用对于空车调配问题的影响，作者构建了基于货物滞留费用的铁路空车调配多品类整数规划模型。文献[3]研究了考虑时间因素的空车调配优化问题。国外空车调整的研究主要解决的是车辆规模的问题（fleet sizing problem），研究的方法主要有线性规划算法、随机优化算法和模拟仿真算法等。文献[4]构建了多阶段铁路货运车辆规模模型，并采用模拟退火算法进行求解。文献[5]同时研究了需求不确定的情况下考虑了车队规模和货物车辆分配问题，采用了两阶段优化算法对随机模型进行了求解。文献[6]假设在未来需求不确定的情况下，考虑包含多种车辆类型的车辆规模问题，作者设计了动态规划和黄金分割相结合的算法进行求解。本文较以往研究不同，问题的提出是基于实际的车流推算应用，且采用了多阶段的空车调配模型，相对于以往单一阶段的分配模型，空车调配的时间更精确，符合了铁路未来精细化管理的方向。

1 空车调整模型输入和输出介绍

为了实现铁路运输精细化管理，提高信息化水平，铁路建设了铁路运输信息集成平台。该平台通过与既有信息系统交换数据以及处理站段报告事件，整合列车、车辆、货物等数据，汇集形成面向货运领域的集中数据环境。

车流推算系统（CFCS）正是在集成平台数据环境下的开发应用，而车流推算过程中又不可避免的需要研究空车调整问题。CFCS采集集成平台的数据，通过推算模型并结合次日承认车计划能够比较准确地预测次日时间段内车站的空车提供量或者车站的空车需求量，为空车调整提供输入条件。

车流推算模型与空车调整模型的关系如图1所示。集成平台提供的数据经过车流推算模型处理后为空车调整模型提供必要的输入条件：（1）路网中车站的空车供给量；（2）路网中车站的空车需求量；（3）铁路网络拓扑结构；（4）计划的时间阶段。空车调整模型主要输出结果为：（1）每个阶段空车调整的数量；（2）空车提供站的空车滞留数量；（3）空车需求站的空车延误数量。

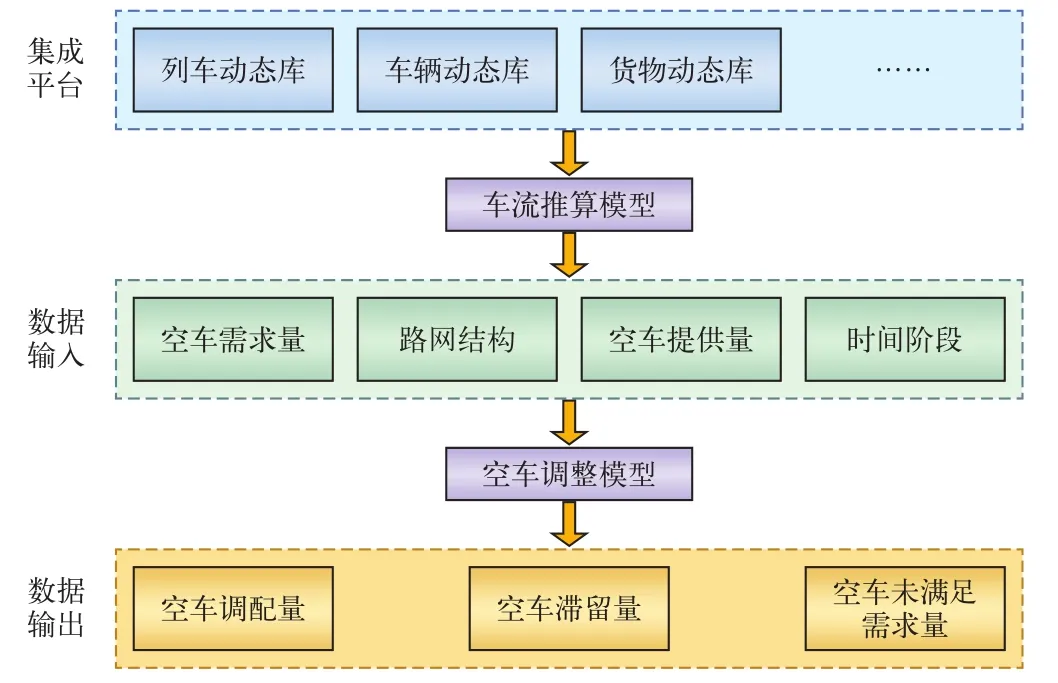
图1 空车调整模型的输入输出内容

2 空车调整模型

2.1 问题描述

空车调整问题就是在铁路运输系统中将空车从空车多余车站合理分配到空车需求车站的问题。空车调整可以考虑单车种或者多车种，如果考虑多种类型的空车，那么就需要考虑空车提供与需求的车种匹配以及车种替代等问题，本文仅考虑单种空车类型。车辆在两个车站之间的运行时间需要根据路网的径路结构来决定。

2.2 数学模型

2.2.1 变量定义

N1：网络中所有的空车提供站点集合；

N2：网络中所有的空车需求站点集合；

T：多阶段（时间阶段）集合， t=0,1,…,Te；

Cj：空车需求站单位空车满足所得收益，j∈N2；

ECij：单个空车单位距离走行的价值，i∈N1，j∈N2；

Lij：空车提供站i到空车需求站j的距离，i∈N1,j∈N2；

HCi：单个空车在一个时间阶段内的滞留费用；

PCj：空车需求站点未满足需求的惩罚值，j∈N2；

ttij：从空车提供点i运行到空车需求点j的运行时间；

Pi(t)：在时间阶段t内空车提供点i提供的空车数量；

Di(t)：在时间阶段t内空车需求点j需要的空车数量；

αij(τ,t)：空车从起点出发的时间阶段为τ，到达终点的时间阶段为t，且τ≤t，则该值为1，否则为0；

χij(t)：表示时间阶段t的空车调配的量；

vi(t)：表示时间阶段t末空车产生站剩余的空车；

ωi(t)：表示时间阶段t的空车滞留的量；

σi(t)：表示时间阶段t的空车不满足的量。

2.2.2 数学模型

目标函数：

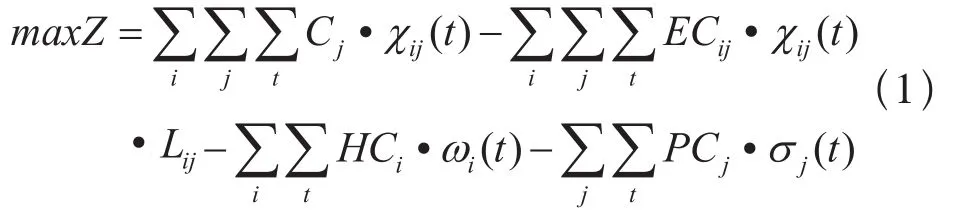
约束条件：

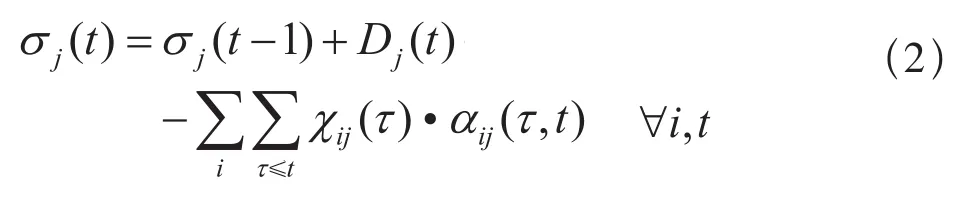
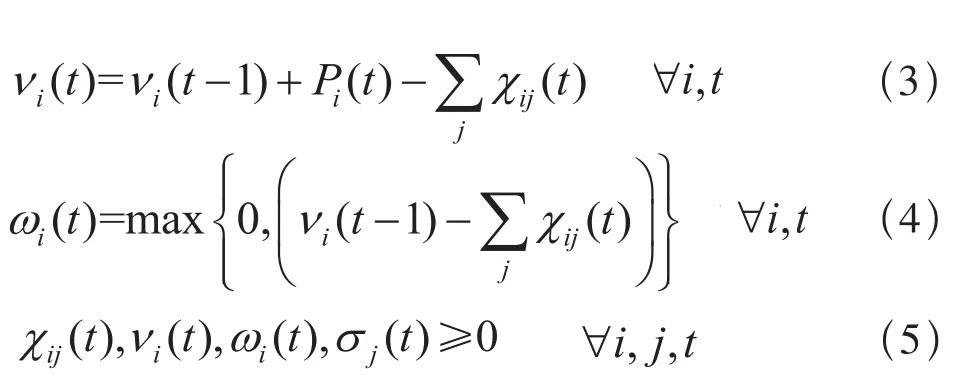
目标函数（1）：表示空车调配计划的综合收益，为多目标决策函数，包含空车调配的纯收益最大化，调配的费用支出的最小化，费用包含：空走费用、滞留费用和需求未满足的惩罚费用。约束条件（2）：表示任意空车需求站在任意时间段内未满足的需求数量。约束条件（3）：表示任意空车提供站在任意的时间段末所剩余的空车数量。约束条件（4）：表示任意空车提供站在任意的时间段内所滞留的空车数量，它是由上一个阶段剩余的空车数量减去本阶段调配的空车数量得出的，也就是说在上一个阶段剩余的空车如果在本阶段内还没有被调配就认为这些空车在本阶段内出现了滞留。约束条件（5）：表示决策变量和中间变量的非负性质。

3 算法

由于该问题复杂程度随着网络节点规模和时间阶段规模增长呈指数级的增长，较难得到多项式求解算法，因此采用模拟退火算法。模拟退火算法（SA，Simulated Annealing）是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。空车调整问题也是一般性的组合优化问题，因此可以利用模拟退火算法进行优化求解。

3.1 初始解

用贪心的局部优化算法取得模拟退火算法的初始解。

3.2 邻域解

邻域解的产生是根据随机选择空车调整量χij(t)，然后在此量的基础上随机浮动Δχij(t)，浮动量位于区间[0.3·χij(t)，-0.3·χij(t)]。

3.3 冷却策略

每次迭代温度采用下面的函数进行控制：

接受函数采用下面的随机函数确定：

从公式（7）可以看出，较差解可以接受的概率由当前循环设置的温度T和目标值的变差量ΔZ共同决定，在温度较高时，较差解被接受的概率较高；温度较低时，较差解被接受的概率较低。

3.4 终结条件

算法的终结条件为迭代时的温度下降到设定温度时或者迭代到一定的次数时目标函数还没有得到优化。

4 算例

考虑简单的路网结构，并假定路网中节点S1～S4为空车提供点，S6～S9为空车需求点，具体信息如表1～表3所示，其中，表2及表3中的空车需求量和提供量都为经验假设模拟数据。需求节点考虑的时间阶段从T2开始，因为提供节点的时间阶段从T1开始，加上两点间的运输时间，因此空车到需求点最早也要到T2阶段。

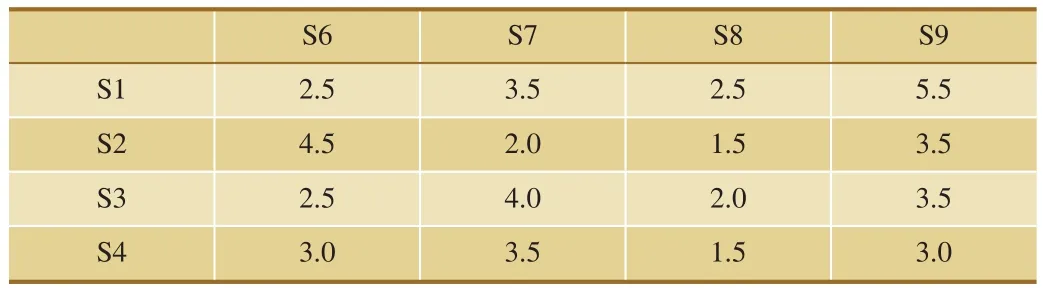
表1 路网中车站之间的最短运行时间

表2 空车需求点在多阶段的空车需求量

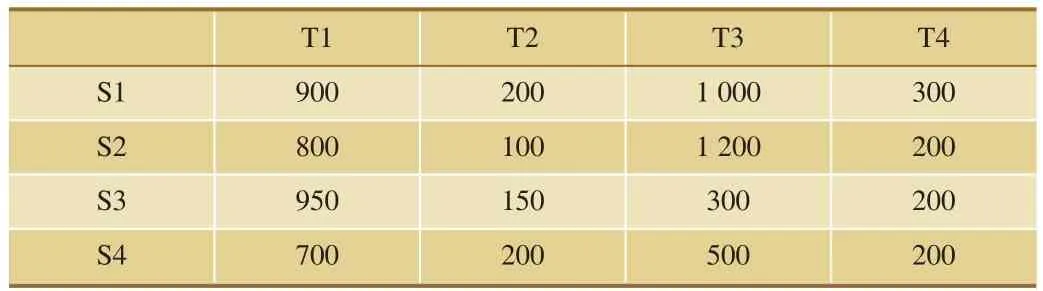
表3 空车提供点在多阶段的空车提供量

4.1 输入条件参数

目标函数中所涉及的费用参数：单位空车每小时走行费用为500元；单位空车需求满足后，所产生的效益为10 000元；单位空车单个时间阶段的空车滞留费用为500元；单位空车单个时间阶段的空车未满足需求的费用为1 000元。每个时间阶段的时长为3 h。模拟退火算法的参数设置如表4所示，参数值的设置根据经验值得到，并结合算例本身进行了验算修正。

表4 模拟退火算法参数设置

4.2 计算结果

通过Java程序实现了模拟退火算法。模拟退火算法迭代优化结果如图2所示。从图中可以看出，前100次迭代目标值收敛的速度较快，100～150次迭代目标收益有缓慢增长，而从150～350次的迭代中，收益稳定维持在7.55 千万元左右，并没有明显的增加，因此，可以认为在150次迭代后的空车调配方案已经达到了优化解，可以作为优化的空车调整方案。

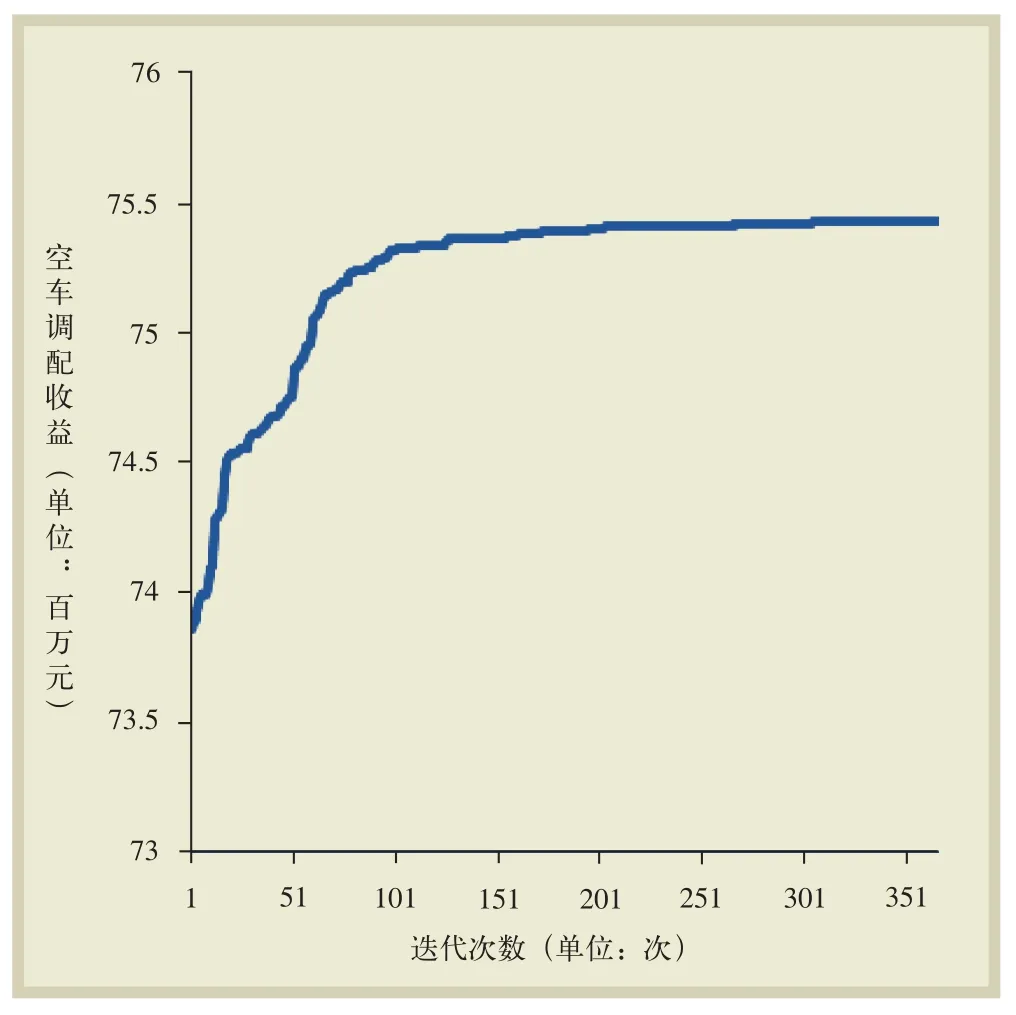
图2 模拟退火算法的迭代优化图

5 结束语

在车流推算研究的大背景下，本文建立了多阶段空车调整优化模型，该模型能够将多阶段的空车调整综合优化，比较符合铁路实际生产中多阶段计划的综合调优，并采用模拟退火算法进行优化，结果表明，该模型在车流推算系统中能较好地处理空车调整的问题。

[1]林柏梁，乔国会.基于线路能力约束下的铁路空车调配迭代算法[J].中国铁道科学，2008，29（1）：93-96.

[2]曹学明，林柏梁.基于滞留费用的空车调配优化方法[J].铁道学报，2007，29（4）：18-22.

[3]程学庆，陆一新，尹传忠，等.基于时间窗的铁路空车调配优化模型及求解[J].中国铁道科学，2007，28（6）：113-116.

[4]Hamid Reza Sayarshad,Keivan Ghoseiri.A simulated annealing approach for the multi-periodic rail-car feet sizing problem[J].Computers &Operations Research,36 (2009):1789-1799.

[5]Hamid Reza Sayarshad ,Reza Tavakkoli-Moghaddam.Solving a multi periodic stochastic model of the rail-car feet sizing by two-stage optimization formulation[J].Applied Mathematical Modelling,34 (2010):1164-1174.

[6]Ryan Loxton ,Qun Lin,Kok Lay Teo.A stochastic fleet composition problem[J].Computers &Operations Research,39 (2012):3177-3184.

责任编辑 付 思

Railway multi-stage empty car adjustment method applied to Car Flow Estimation System

SHAN Wu
( Information Center,National Railway Administration of People’s Republic of China,Beijing 100891,China)

Empty car adjustment model researched in this paper was part of Car Flow Estimation System.The car fow estimation model could be used to calculate the demand and availability of empty car precisely on different time periods.According to the dynamic change characteristics of empty car adjustment problem of railway network,a dynamic multi-stage empty car adjustment model was set up.The empty car stranded costs and unsatisfed demand penalty costs related to time factor were considered in the object function.The Heuristic Algorithm of simulated annealing was designed to solve the function.Finally,a simple network was taken to verify the model,and the results indicated that the model could handle the empty car adjustment problem under dynamic environment.

railway transportation;multi-stage empty car adjustment;service network of time and space;railway network;Heuristic Algorithm;Car Flow Estimation System

U292∶TP39

A

1005-8451（2016）06-0005-04

2015-12-20

单 武，高级工程师。