天然气消费需求分析及预测

卢全莹，柴 建，2，朱 青，邢丽敏，邓俊丽

（1.陕西师范大学国际商学院，陕西 西安 710062；2.中国科学院国家数学与交叉科学中心，北京 100190）

1 引言

近年来，天然气以其环保经济、安全可靠等优点被广泛应用于发电、化工工业、城市燃气、压缩天然气（Compressed Natural Gas，CNG）等工业生产和居民生活领域。BP世界能源统计年鉴（2013）表明，2012年石油占全球能源消费的比重持续下滑，增长幅度仅为0.9%，而天然气增长幅度为2.2%，占基础能源消费的23.9%。《2012年国内外油气行业发展报告》称，2012年我国天然气表观消费量1471亿立方米，较2011年增长13%，其中进口量达到425亿立方米，增长31.1%，对外依存度达到29%。我国天然气消费市场的日益扩大，对天然气的开发及输送管道建设、维护等提出了更高的要求。同时，“十二五”规划明确将攻克开发关键技术作为主要任务，为“十三五”页岩气大规模开发奠定基础。在这样的政策背景下，对天然气消费量进行合理准确的预测，一方面对天然气管道规划建设、生产管理及输配气的调度具有重要意义；另一方面，可以有效节约成本，减少输配气费用，更好地满足生产和生活需求。随着集成人工智能技术的快速发展，预测方法从传统的时间序列平滑法、回归模型法、趋势外推法与相关分析法发展到现在，模糊集、粗糙集、支持向量机、遗传算法等智能化方法已被广泛引入到能源预测中。本文将采用在能源预测中具有明显优势的现代人工智能预测方法——RBF神经网络分位数回归模型对我国天然气消费量进行分析及预测。

2 相关研究

截止目前，国内外对能源需求的研究文献相对丰富，对天然气消费的分析及预测也是屡见不鲜。能源需求问题越来越多地吸引到了科研工作者的目光。就相关的问题，本文从多个角度与层次对天然气消费问题进行了探讨。主要的研究集中在以下两方面：

（1）天然气消费的驱动因素：在驱动因素方面，大量研究表明能源的需求量与经济增长、人口数量、经济结构等因素有关。Das等［1］首先对1980－2010年孟加拉国天然气消费量与实际GDP进行了格兰杰因果检验，发现GDP对天然气消费量具有显著促进作用，反之则无明显影响。Apergis和Payne［2］对天然气消费与经济增长之间关系作出进一步研究，建立1992－2005年期间67个国家天然气消费量的多元误差修正模型，并进行异质面板协整检验，得出天然气消费量和实际GDP、实际资产投资总额及劳动力人数之间存在长期均衡关系，且天然气消费量与经济增长之间存在双向因果关系，天然气消费弹性系数估计值为0.652，这一数值略低于可再生能源的0.76，远高于煤炭的－0.142到－0.251，即经济增长对天然气消费量有较强的依赖性。Kankal等［3］通过构建人工神经网络和回归分析方法，以社会经济和人口统计学变量为影响因素对土耳其的能源消费进行预测，测试变量有国内生产总值（GDP）、人口、进出口额和就业，经过逐步回归得出GDP、人口、进出口额四个变量可以有效地预测该地区能源消费，最后预测2014年土耳其能源消费将会在117.0－175.4百万吨油当量之间浮动。周跃忠、李婷［4］通过分析全球及我国的天然气消费现状，认为经济发展水平、天然气价格和可替代能源价格是影响天然气消费的主要因素，并对每个影响因素进行了详细的分析。史立军、周泓［5］综合考虑了人口、经济、环境等因素的基础上，运用系统动力学方法建立了我国天然气供需趋势预测模型，对我国2010年到2030年的天然气供应量、消费量、净进口量、对外依存度、二氧化碳排放量等进行了预测，并通过对天然气消费主要参数的灵敏度分析深入研究了其对消费状况的影响。预测结果显示，未来我国天然气供应量和消费量均将快速增长，但由于可采储量的限制，天然气供应量在2028年达到国内生产能力的最大值后开始逐年下降。由于经济的快速增长，天然气需求量持续上升，导致进口量的不断增加，天然气资源对外依存度将不断提高。

（2）天然气消费的预测方法：在短期预测方面，Sánchez-U＇beda［6］和 Gutierrez等［7］分别作了研究，前者提出了一种统计分解模型，对西班牙工业用气的日度数据进行时间序列分解，得到了天然气需求量的短期预测；后者以西班牙1973－1997年天然气消费量为样本数据，利用随机Gompertz创新扩散（Stochastic Gompertz Innovative Diffuse）模型对1998－2000年天然气消费总量做出预测，验证了该模型的预测结果与真实值的拟合度明显高于其它随机扩散增长模型，如逻辑（扩散－创新）模型和对数正态（扩散－非创新）模型。随后组合预测模型逐渐得到应用，Khotanzad和Elragal［8］提出两阶段人工神经网络方法，利用多层前馈神经网络和功能连接神经网络组合预测出美国六家公用事业天然气用量；Xu Gang和 Wang Weiguo［9］将二阶多项式曲线模型（2nd Order Polynomial Curve model）与移动平均模型（Moving Average Model，MA）结合，建立了PCMACP模型，对2007－2008我国天然气需求总量进行预测分析，所得预测值与真实值的平均误差百分比为3.82%，这显著低于利用传统的二阶多项曲线模型、BP神经网络模型以及灰色预测模型预测所产生的误差。Soldo Bozidar［10］对天然气预测现状进行了总结，分别从天然气研究发展历程、研究范围、预测视角（小时／天／月／年／组合）、数据类型、预测工具等方面进行了详细阐述，并指出Hubert曲线模型和灰色模型将会是预测的主要工具，在较小范围内最优化工具和经典回归工具的结合将可能是发展方向。李君臣，董秀成，高建［11］利用系统动力学模型，对我国未来天然气消费量进行中长期预测。预测结果显示，我国未来天然气消费量将保持迅速增长的态势，预计2020年达到1830.0×108m3，2030年达到3027.4×108m3；天然气消费结构也将发生变化，化工用气、工业燃料用气占消费总量比例有所下降，但占比数量仍然最大，发电用气和第三产业用气占比有所上升，而居民消费用气占比先升后降。罗东坤，徐平［12］在对传统的BP神经网络运用附加动量法进行改进的基础上，建立神经网络模型。预测结果表明，我国未来10年天然气需求仍很强劲，而国内天然气供应难以满足长期需求，政府需要制定相应的天然气供需策略。周子卜，李莉，张淑英［13］运用不确定分析法的灰色系统理论，选取我国1990－2004年天然气消费量数据，构建了天然气需求增长灰色系统预测模型GM（1，1）。

通过对前人的研究总结发现，多数学者比较赞同的观点是：基于历史数据的ARMA方法和指数平滑法更适合短期预测；灰色预测方法能够用于范围较广的长短期预测，但精确度有所下降；人工神经网络具有自适应、自组织和实时学习的特点，适用于动态天然气消费预测及动态训练系统，且具有较高的预测精度等。但是单纯的神经网络算法是在无约束的非线性条件下将所有信息数字化，虽然精确度很高，但是在预测方面却不能有效的反映出现实经济变量之间关系的不确定性。于是，为了找到一种可以避免确定性预测缺陷的新方法，有学者开展了大量概率性区间预测的研究工作，如分位数回归方法结合神经网络模型，给出了一定置信水平下的概率化区间预测结果。这样就把在非线性预测方面具有较高精度的神经网络和凸显局部影响的分位数回归很好地结合起来，得到良好的预测效果。例如，何耀耀［14］等将RBF神经网络和分位数回归两种方法相结合构建模型，并利用时间序列数据给出了一天中每个时刻电力负荷的完整概率分布函数。

文章结构如下：首先，利用通径分析筛选出我国天然气消费的核心驱动因素。其次，构建RBF神经网络分位数回归模型对我国天然气消费进行预测。模型构建时以非线性分位数回归为理论基础，建立天然气概率密度分位数回归预测模型，并采用标准的梯度优化算法估算出模型的参数向量。运用交叉验证方法确定RBF神经网络基函数的中心、宽度以及惩罚参数的值。拟合出不同分位数水平下的天然气消费量，并计算比较各分位数水平下的相对误差。最后，选取误差最小的中位数回归进行天然气消费预测。

3 核心影响因素提取

在影响因素研究中，大部分研究采用多元回归分析方法，但该方法的缺点是不能消除多重共线性。为了解决这一问题，数量遗传学家Sewall Wright于1921年提出来的一种多元统计技术——通径分析。通径分析是简单相关关系的进一步发展，在多元回归的基础上通过对自变量与因变量之间表面直接相关性的分解，通过直接通径、间接通径和总通径系数来研究自变量对因变量的直接作用、间接作用以及综合作用，从而为统计决策提供可靠的依据，在众多领域得到广泛应用。例如Chai Jian等［15］将此方法应用在分析石油价格影响因素的研究中。

从大量的文献阅读可知，影响天然气消费量的因素很多，涉及各个方面，而且因素间的相互关系比较复杂。所以，本文基于文献综述提及的国内外研究及我国的现状，将分别从需求和供给、替代能源、成本因素和国家政策等角度综合考虑天然气产量、人口、城镇化率、GDP、城镇人均消费、工业燃料出厂价格、电价 （X1，X2，…，X8）等影响因素对天然气消费（Y）的影响，选取1990－2011年的年度数据（本文数据来源：WIND数据库、《中国统计年鉴》），利用通经分析提取我国天然气消费量的核心影响因素。

表1 正态性检验

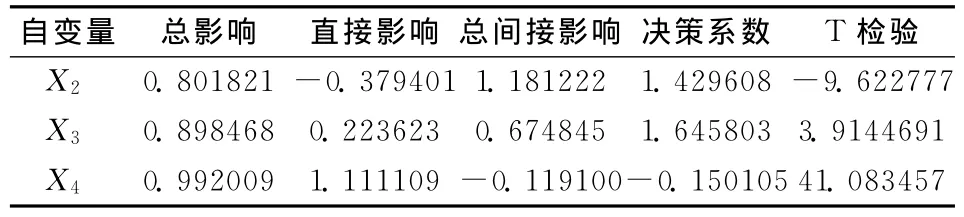
表2 各影响因素对天然气消费的通径分析表

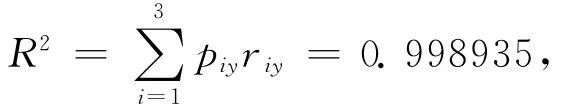
4 模型构建及结果分析

4.1 RBF神经网络结构

针对传统BP神经网络中出现的收敛过分依赖初值和局部收敛等问题，Moody和Darken［16］在20世纪80年代末提出了RBF网络，它是以径向基函数作为隐含层神经元激活函数的三层前向型神经网络，具有较快的运算速度、较强的非线性映射能力和较好的预报效能。它通常具有三层网络结构，包括输入层、隐含层、输出层，网络模型的拓扑结构如图1所示。

RBF神经网络结构通过两层映射关系实现，分别是输入层到隐含层空间的非线性变换和隐含层空间到输出层空间的线性变换。RBF神经网络结构的确立，是通过映射函数（径向基函数）的学习，确定隐含层神经元基函数的数据中心cj、方差σj以及隐含层到输出层的权值wj，i，从而完成输入到输出的映射。

4.2 分位数回归

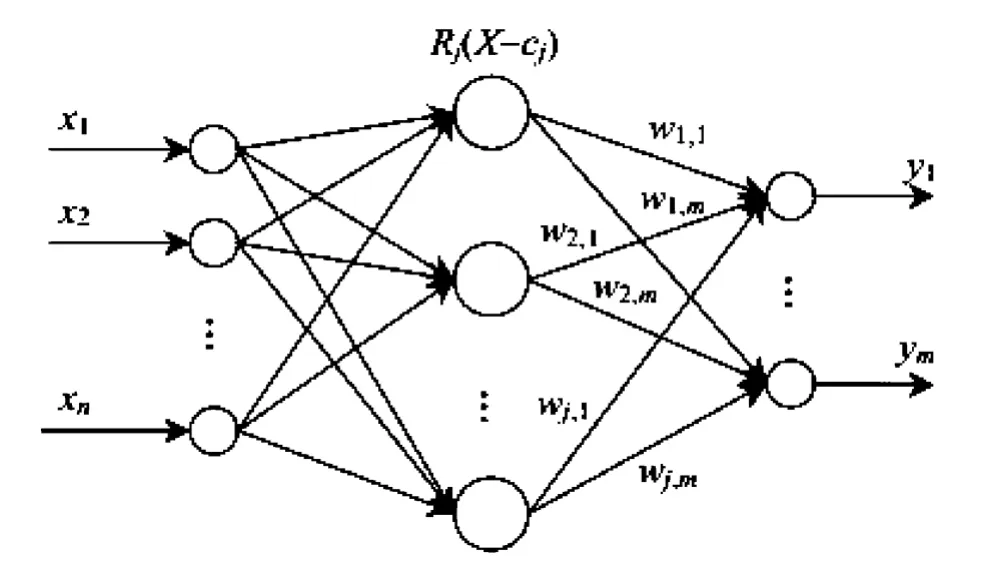
图1 RBF神经网络结构

Koenker和Basset［17］于1978年提出了分位数回归理论，该理论刻画了当给定回归变量X时，响应变量Y在不同分位数下的变化趋势，度量了回归变量在分布中心、上尾及下尾的影响，突出了局部之间的相关影响。假设Y受到k个因素X1，X2，…，Xk的影响，分位数回归表示为：

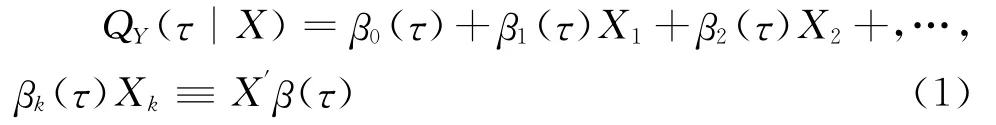
式中：QY（τ｜X）为响应变量Y在解释变量X＝［X1，X2，…，XK］′给定下的条件τ分位数；τ∈ （0，1）为分位数点，决定了在因变量的那个分位点水平上 进 行 回 归；β（τ） ＝ ［β0（τ），β1（τ），β2（τ），…，βk（τ）］′，为回归系数向量。

4.3 基于RBF分位数回归的预测模型

Taylor［18］提出了基于单层神经网络的分位数回归模型：

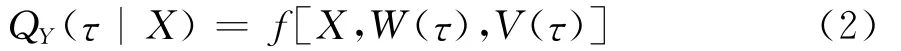
该式中：W（τ）＝ ｛wjk（τ）｝j＝1，2，3，…，j；k＝1，2，…，K为输入层到隐含层的连接权重向量，V（τ）＝｛vj｝j＝1，2，…，J为隐含层与输出层之间的连接权重向量；K为隐含层节点数；f为一个非线性函数，其表达式为：

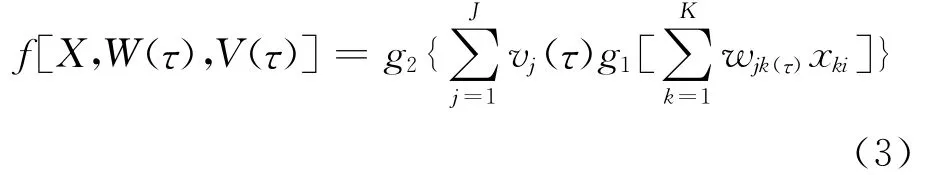
公式（3）体现了由解释变量X到响应变量Y的非线性结构。本文中，由于天然气的年消费量数据具有连续性，在众多的神经网络类型中径向基函数神经网络适合拟合连续变化数据，故本文神经网络选取RBF神经网络方法。

神经网络分位数回归模型式（2）中参数向量W（τ）、V（τ）的估计可以通过下列式子的最优解得到：

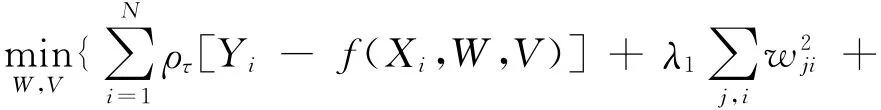
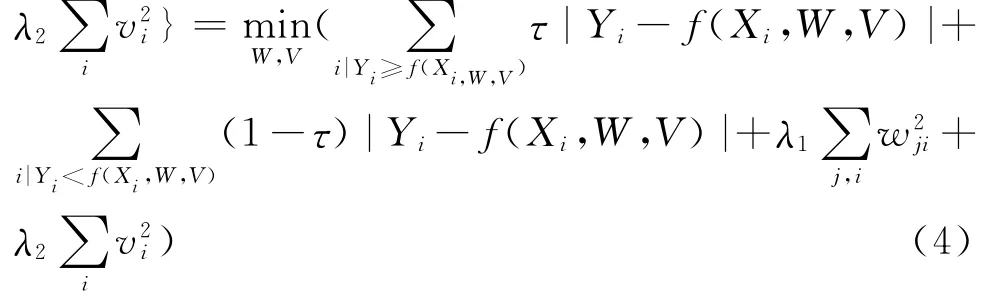
式中λ1、λ2为惩罚参数，是为了避免网络结构陷入过度拟合的状态而设置的。惩罚参数λ1、λ2和隐含层节点数K的最优取值也可以用交叉验证方法确定。参数向量W（τ）、V（τ）的估计可以使用标准的梯度优化算法进行求解，将得到的参数估计量其分别代入式（2），就可以得到Y的条件分位数估计。如下式（5）：

4.4 基于RBF分位数回归的天然气预测分析

4.4.1 数据选取

本文选取1990年至2011年我国天然气消费总量的数据作为输出变量，将通径分析筛选出的3个核心影响因素：国民生产总值、总人口和城镇化率作为输入变量，构建RBF神经网络分位数回归模型。分两个阶段进行，第一阶段：选取1990－2006年数据作为训练样本，对模型拟合并得出各个参数值，选取2007－2011年数据作为测试样本，并预测该时间段内我国天然气消费量。将2007－2011年天然气消费量预测数据与统计局公布的实际值作对比，计算预测误差。第二阶段：以1990－2011年天然气消费量为训练样本，利用上述所得参数值对2012－2020年天然气消费量进行预测。模型经训练所得，RBF神经网络的最大迭代次数为1000，神经网络结构为3－1－1.即输入层的节点数为3，隐含层为1，输出层为1；分位数回归模型的惩罚参数λ1、λ2都为0.00001，RBF神经网络核函数的宽度σ为10。所有数据进行标准化处理，如式（6）所示：

式中：Xs为标准化处理后的样本向量，Xt为原样本向量，为列向量的平均值，S为列向量的标准差。

本文给出了2012－2015年天然气消费核心影响因素的基准情景估计值，根据我国“十二五规划”，人口年均自然增长率控制在7.2‰以内。我国国内生产总值在2015年将达到55.8万亿元，年均增长7%，故本文以7%的增长率计算GDP变化量。2015年城镇化率要达到54%以上，“十二五”第一年（2011）的城镇化率已达到51.27%。十八大后，中国政府致力于改变贫富差距、保持经济的持续发展，而完成这两个目标的最重要的一个措施就是城镇化，通过城镇化来缩小贫富差距，在城镇化过程中基础设施、产业的转移和结构调整将带动大量的投资和就业。因此未来城镇化的速度不会下降，按照十八大后大部分人口专家的估计，2020年中国的城镇化将达到60%以上。按照这个预期，城镇化的年增长率将达到2%左右，本文以增长率2%的标准来设定2011－2020年中国的城镇化率。具体结果见表3。

4.4.2τ分位数的确定

RBF神经网络分位数回归中，预测结果因分位数取值不同而有差异。反映在本文中，就是不同概率密度水平下，天然气消费量预测结果的不同。如表4所示为不同分位数水平下天然气消费预测量。选取1990－2006年数据为训练样本，RBF神经网络经训练后，对2007－2011年天然气消费量进行预测，并与2007－2011我国天然气实际消费量进行对比。由表4可以看出，分位数τ＝0.1时，预测误差最小为3.02%，相应的天然气走势图也与真实值对应曲线最为接近，所以本文数据最合适的RBF神经网络分位数模型应该选取的τ值为0.1。

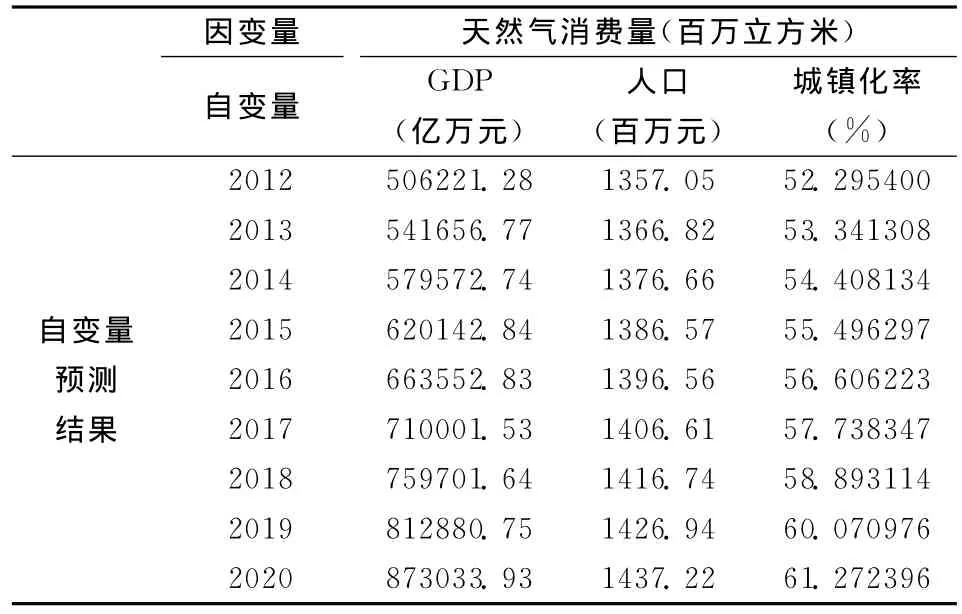
表3 天然气消费核心影响因素基准情景

表4 不同分位数水平（τ）下天然气消费预测结果差异比较

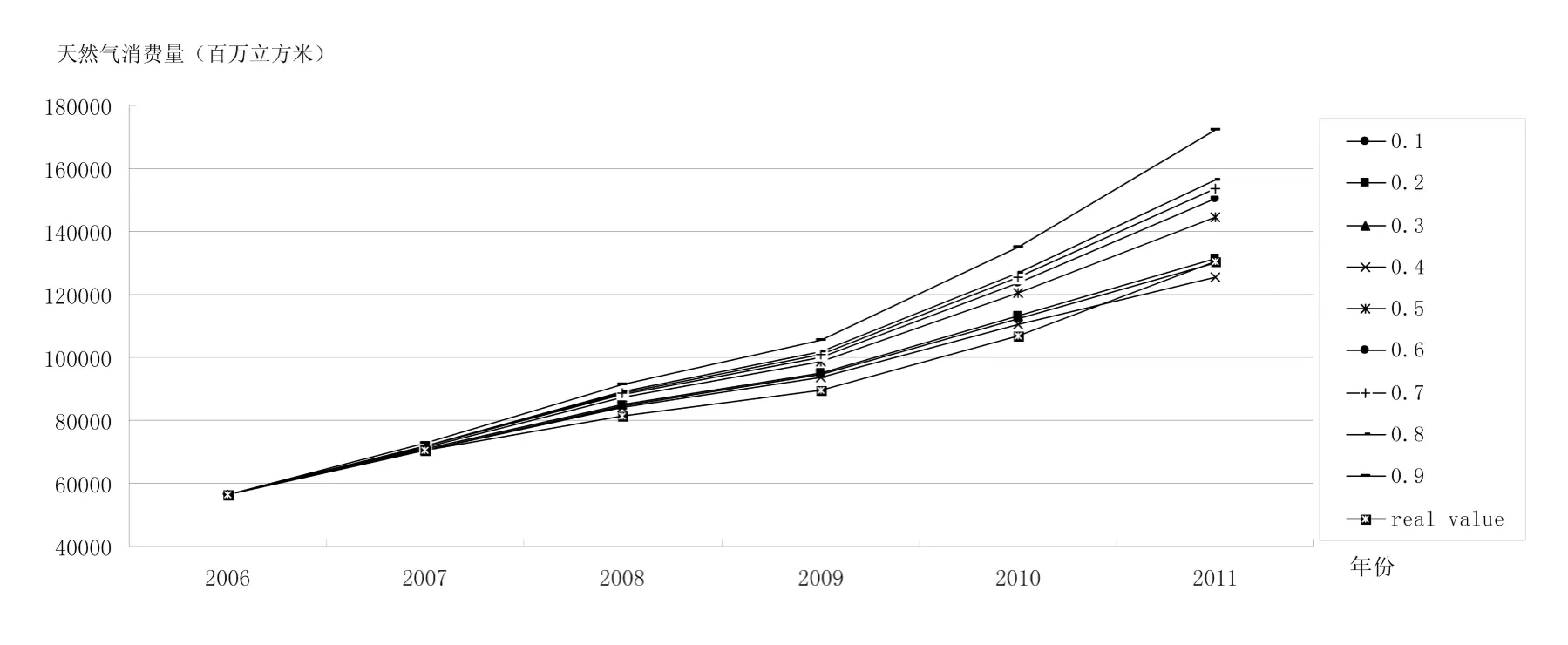
图2 不同分位数水平下天然气消费量走势图

对模型进行训练，将所得1990－2011天然气消费量拟合数据与真实数据比较，计算预测平均误差为0.08%，即模型的拟合精度高达99.92%，这显示了RBF神经网络分位数回归在进行复杂非线性预测方面的优越性。2012－2020年的我国天然气消费量预测值的具体结果见表8。

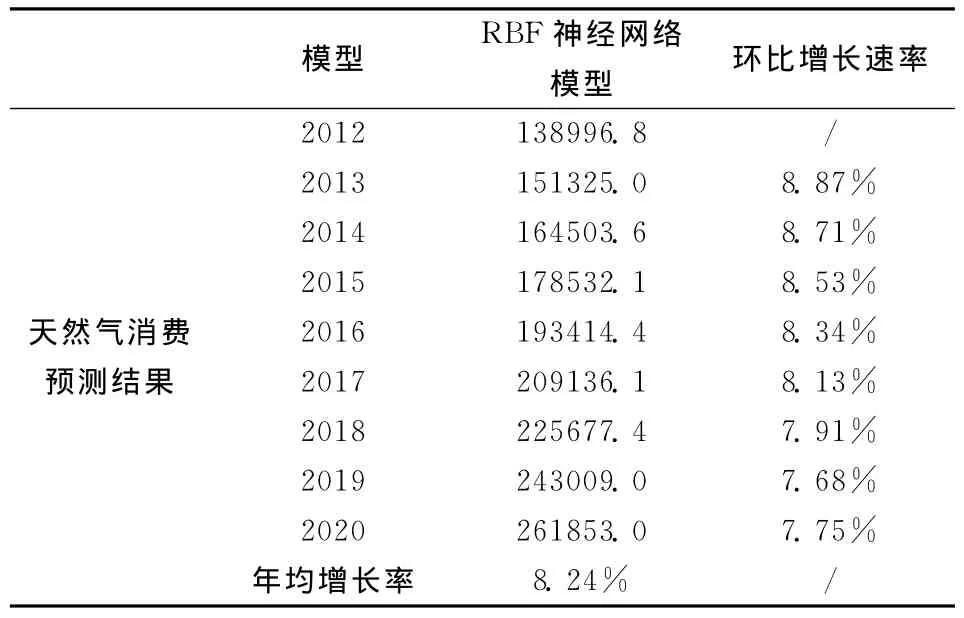
表5 天然气消费需求（百万立方米）预测结果

预测结果表明，2012年我国天然气消费总量预测值为138996.8百万立方米，而2012年天然气实际消费量为132774.13百万立方米，相对误差为4.69%，年均增长率为8.24%，在可接受范围内，比较合理。虽然预测值略大于真实值，但是天然气作为新兴的清洁能源，发展速度快、发展潜力大，其预测值略大于真实消费值是合理的。因为，随着时间的变化，科技进步加快，势必会提高能源的利用率。从环比增长速率来看，天然气消费量增长速度减缓。原因可能在于太阳能、生物质能、地热能等清洁能源的推广应用、我国GDP增速放缓、天然气替代能源价格下降等原因。但是从年均增长速率和1990－2020年我国天然气消费量的整体走势来看，天然气的消费量还是一直处于平稳上升状态。

5 结语

本文对我国天然气消费进行深入剖析，利用通径分析方法筛选核心影响因素，发现人口和城镇化率是天然气消费的主要推动因素，GDP是天然气消费的主要限制因素。这与目前我国的能源消费结构相关，我国能源现状是“多煤，少气”，能源消费还是主要以煤炭为主。但近年来环境污染的巨大压力使得我国正在逐渐实现能源结构的转型，所以天然气在能源消费中占比增加，呈现出增长趋势。模型的预测结果也表明，随着我国能源消费结构的改变，天然气相对于煤炭的清洁优势使得我国天然气消费量总体呈现增长趋势。保守估计“十二五”期末中国天然气需求量将达到近178532.1百万立方米，2020年中国天然气消费达到近261853.0百万立方米，2011－2020年的年平均需求增长率达到8.24%。这种现状虽然表明我国在能源结构转型中取得了一定成绩，但同时也为我国应对天然气需求高峰提出了挑战。政府相关部门应提前采取措施对天然气的使用进行统筹规划，如合理分配、价格调整等。其次，应该加大天然气资源勘探开发力度，推进煤层气、页岩气等非常规油气资源开发利用，加大天然气在能源储备与调峰方面的作用。完善国内油气主干管网，统筹天然气进口管道、液化天然气接收站、跨区域骨干输气网和配气管网建设，初步形成天然气、煤层气、煤制气协调发展的供气格局等。

［1］Das A，McFarlane A A，Chowdhury M.The dynamics of natural gas consumption and GDP in Bangladesh［J］.Renewable and Sustainable Energy Reviews，2013，22（8）：269－274.

［2］Apergis N，Payne J E.Natural gas consumption and economic growth：A panel investigation of 67countries［J］.Applied Energy，2010，87（8）：2759－2763.

［3］Kankal M，Akpınar A，Kümürcü M I·，et al.Modeling and forecasting of Turkey’s energy consumption using socio-economic and demographic variables［J］.Applied Energy，2011，88（5）：1927－1939.

［4］周跃忠，李婷 .天然气消费影响因素探究［J］.商业现代化，2008，553（10）：187－188.

［5］史立军，周泓 .我国天然气供需安全的系统动力学分析［J］.中国软科学，2012，（3）：162－169.

［6］Sánchez-U＇beda E F，Berzosa A.Modeling and forecasting industrial end-use natural gas consumption［J］.Energy Economics，2007，29（4）：710－742.

［7］Gutiérrez R，Nafidi A，Sánchez R G.Forecasting total naturalgas consumption in Spain by using the stochastic Gompertz innovation diffusion model［J］.Applied Energy，2005，80（2）：115－124.

［8］Khotanzad A，Elragal H，Lu T L.Combination of artificial neural-network forecasters for prediction of natural gas consumption［J］.Neural Networks，IEEE Transactions on，2000，11（2）：464－473.

［9］Xu Gang，Wang Weiguo.Forecasting China＇s natural gas consumption based on a combination model［J］.Journal of Natural Gas Chemistry，2010，19（5）：493－496.

［10］Soldo B.Forecasting natural gas consumption［J］.Applied Energy，2012，92（4）：26－37.

［11］李君臣，董秀成，高建 .我国天然气消费的系统动力学预测与分析［J］.天然气工业，2010，30（4）：127－129.

［12］罗东坤，徐平 .基于改进BP神经网络的天然气需求预测［J］.油气田地面工程，2008，27（7）：20－21.

［13］周子卜，李莉，张淑英 .基于灰色理论的天然气需求预测［J］.天然气勘探与开发，2006，29（1）：74－76.

［14］何耀耀，许启发，杨善林，等 .基于RBF神经网络分位数回归的电力负荷概率密度预测方法［J］.中国电机工程学报，2013，33（001）：93－98.

［15］Chai Jian，Guo Ju-E，Meng Lei，et al.Exploring the core factors and its dynamic effects on oil price：An application on path analysis and BVAR-TVP model［J］.Energy Policy，2011，39（12）：8022－8036.

［16］Moody J，Darken C J.Fast learning in networks of locallytuned processing units［J］.Neural computation，1989，（2）：281－294.

［17］Koenker R，Bassett G.Regression quantiles［J］.Econometrica，1978，46（1）：33－50.

［18］Taylor J W.A quantile regression neural network approach to estimating the conditional density of multiperiod returns［J］.Journal of Forecasting，2000，19（4）：299－311.