基于聚类分析的案例距离决策模型
陈 晔,孙汪泉,徐海燕
(南京航空航天大学经济与管理学院,江苏 南京 211106)
1 引言
多属性决策分析(MCDA)能帮助决策者按照一定准则对多个项目进行排序和选优,近年来,随着研究的不断深入,MCDA已经在环境、经济以及社会评估等方面取得了广泛的应用[1]。
MCDA问题的解决一般分为三步:(1)问题模型构建,包括对决策者目标的确定、评价指标的确定与度量,以及确定所有可能的备选方案。(2)决策者的偏好设置。(3)实施评价,或者辅助决策者用适当的模型评价备选方案。
从决策参数获取途径来看,MCDA有两大类,一类是直接交互式决策方法,通过直接交互方式如两两比较获得决策者的偏好信息;第二类是基于案例学习的交互式决策方法,这类方法借鉴统计和数据挖掘的思想,通过对决策者提供具有代表性的决策案例进行训练学习,实现参数拟合,获取决策者的偏好信息,从而有效地提升了决策的效率和精度。案例集一般可以包括:(1)决策者历史案例,(2)假定但具有现实意义的案例,(3)备选方案集中具有代表性的子集。这类方法对决策者信息提取要求难度低,决策者更容易理解和提供相关信息,从而成为多属性决策理论研究的一个热点。
基于案例学习的MCDA方法可分为两大类。其中显性偏好法,如UTA法[4]或基于案例的距离模型[5],即先预设决策函数,函数包含一些未知的参数,通过对案例集进行拟合优化计算确定。而在隐性偏好法中,不预先给定决策函数,如优势关系粗糙集[6]和 ELECTRE TRI辅助法[7],最优化参数的获取是对案例集建立语言判断规则或者两两对比学习实现的。
基于案例距离决策模型(Case-based Distance Approach)首先由本文作者提出,用于解决筛选选优问题[9],然后通过系统地拓展,解决了分类问题[5,10]。沿着这一方向,廖貅武等[11]研究了案例信息不确定下的多属性分类方法,并将该方法扩展到群决策分类问题的研究[2-3]。王翯华等[12]研究了对语言类信息的分类模型,王坚强等[13]提出用聚类方法解决信息不完全确定的决策问题。
本文是对该方法用于解决多属性排序问题的理论拓展,特别是针对评价对象数量比较多时,用前述方法构建模型比较复杂的问题,提出一种用聚类分析和案例距离相结合的方法,结合帕累托约束约简条件,简化了决策模型,提升运算效率,最后,用实例说明了处理评价对象的全排序问题。
2 基于聚类的案例距离决策分析框架
2.1 多属性决策问题描述
首先构建MCDA问题模型,本文定义备选方案集为A= {a1,a2,…,an},评 价 指 标 集 为C={c1,c2,…,cq}。对于任意的i(i=1,…,n)和j(j=1,…,q),定义为方案ai对应指标j的度量值,该度量值是一个客观值,不掺杂任何偏好影响。所有的构成一个vj的决策矩阵mj。如图1所示。
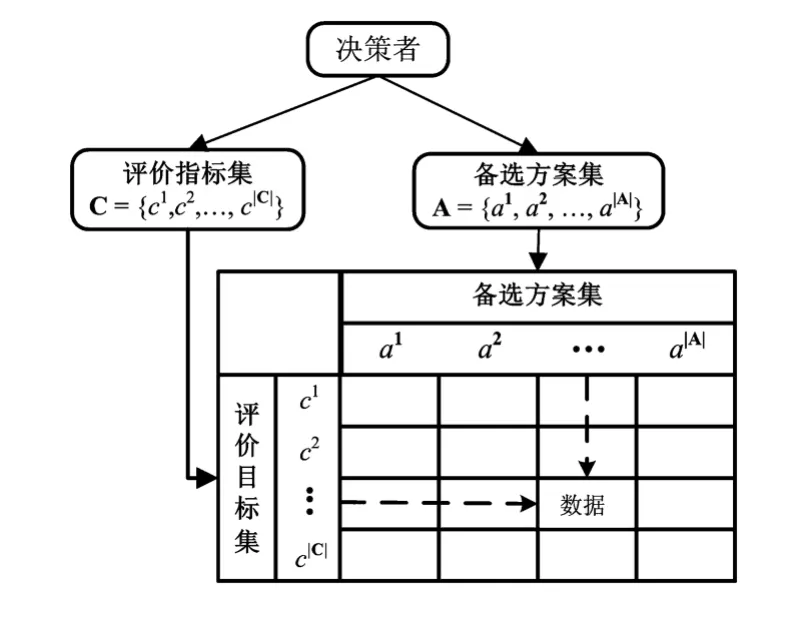
图1 MCDA决策矩阵
对于MCDA问题来说,最重要的问题是决策者偏好的设置。一般来说,决策者偏好可以分为两部分:(1)度量值的主观标准化;(2)评价指标的权重。其中,度量值的主观标准化需要根据决策者的需求和目标,将原值通过标准化处理得到一个标准值,来代表决策者的偏好程度。
2.2 基于案例距离决策方法流程
基于案例距离的决策方法的主要思想是先依据案例集的决策数据获取指标权重,再利用该指标权重对全部数据集决策处理,具体流程如图2所示,主要包括:(1)确定案例集以及正负理想点;(2)对决策矩阵进行规范化处理;(3)建立基于距离的数学模型,获取各指标权重;(4)根据指标权重,分别计算数据集中的数据到正负理想点的距离;(5)根据决策要求输出决策结果。
2.3 基于聚类的典型案例选取方法
当备选方案数量比较大、或者有大量度量值相近,用前文所述案例距离方法解决时,对专家样本的提取和样本排序是有难度的,本文采用聚类的方法,先将备选方案集进行聚类,再将几个聚类的中心作为样本,由专家对聚类进行排序。
图3为基于聚类的案例距离决策模型框架图,共包括四大模块:(1)数据的采集和整理;(2)基于聚类分析,从全部数据集中选取样本;(3)基于案例距离优化模型的构建;(4)对全部数据集决策处理。
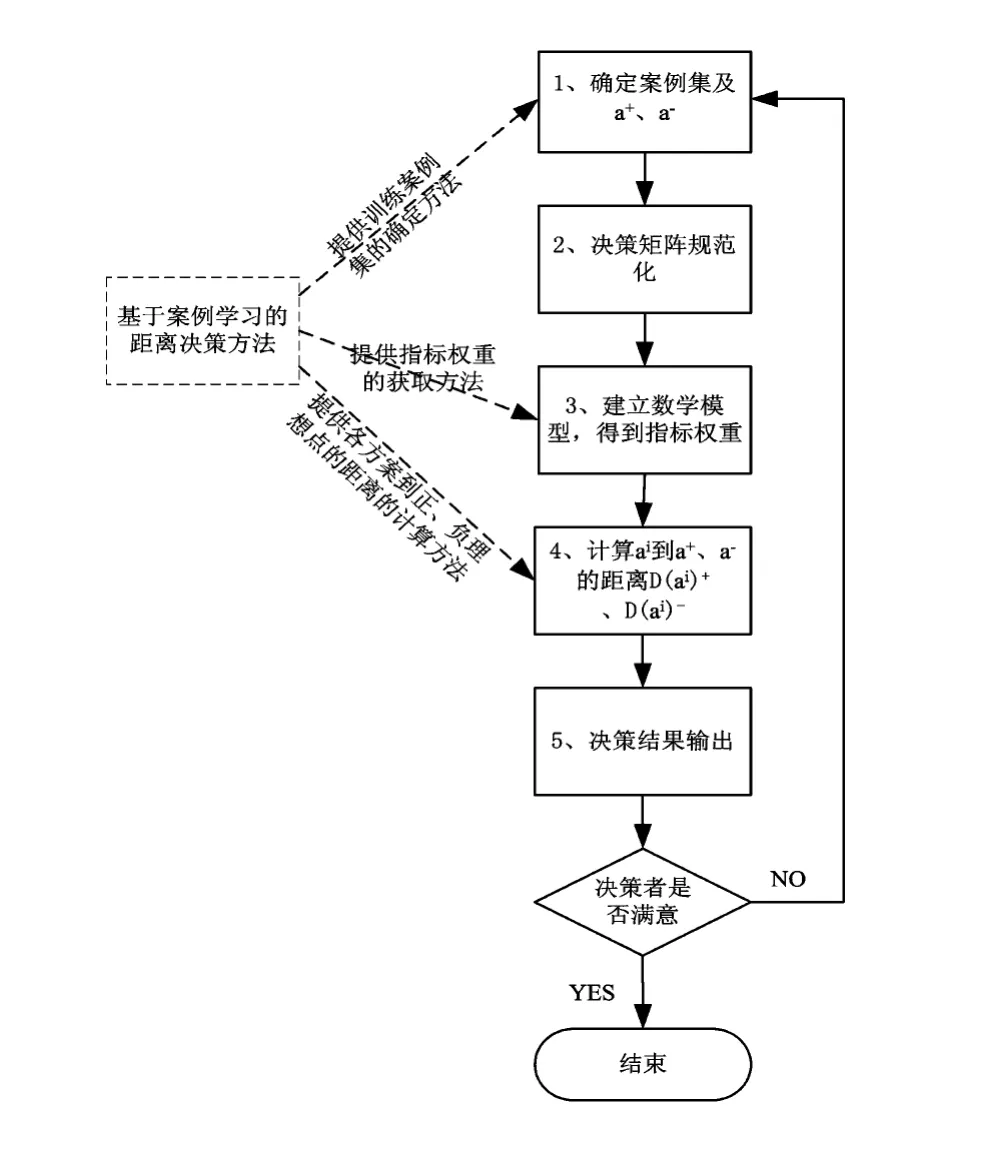
图2 基于案例距离决策方法流程图
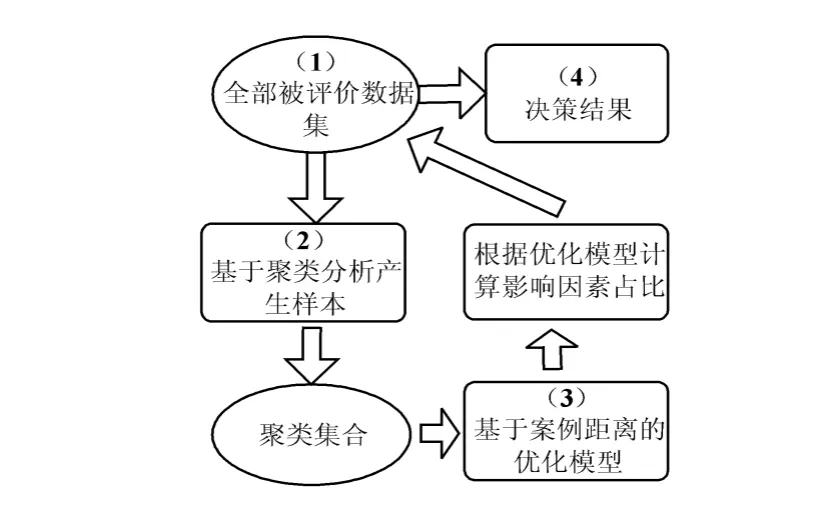
图3 基于聚类的案例距离决策模型框架图
聚类是为了达到更好地理解研究对象的目的,将看似无序的对象分类到不同的类或者簇的一个过程,使得同一个簇中的对象有很大的相似性,而不同簇间的对象有很大的相异性。聚类分析是通过数据建模简化数据的一种方法。依据研究对象(样品或指标)的特征,对其进行分类的方法,减少研究对象的数目。传统的统计聚类分析方法包括系统聚类法、分解法、加入法、动态聚类法、有序样品聚类、有重叠聚类和模糊聚类等。
k-均值算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法首先从n个数据对象通过一定的算法选择k个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到聚类中心不变或变化很小为止。一般采用均方差作为标准测度函数来决定其相似度。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。不同研究者对于同一组数据进行聚类分析,所得到的聚类数未必一致。
3 案例距离决策模型构建
3.1 基本假定
决策者的任务是将方案集A按照评价指标集C进行排序。有|A|=n个备选方案和|C|=q个评价指标,备选方案ai对应评价指标cj的值为,假定mij∈R,那么决策矩阵中的每一行都是Rq中的一个分量,称之为结果分量。我们隐含约定评价指标集是完全按照决策者偏好的结果分量确定的。我们更进一步假设:
决策者能确定最优(最劣)结果分量,定义a+∈Rq(a-∈Rq),称之为为理想点(负理想点)。
选择聚类中心点集合T= {t1…,tr,…,tm},|T|=m并且tr(r=1,…,m)是T中的一个例子,tr上第j个评价指标的值定义为mj(tr)。
假定决策者能够给聚类中心点集合T中的元素排序,并把它重新排列成一个递减序列,则存在这样一个关系,对于1≤g≺h≤m,如果决策者认为tg优于th,记为tg≻th,如果决策者认为tg跟th同样好,记为tg~th。
3.2 帕累托约简
在资源配置中,如果至少有一个人认为方案X优于方案Y,而没有人认为X劣于Y则认为从社会的观点看亦有X优于Y。这就是帕累托标准。
定义1:对于聚类中心点集合T中的任意两个元素tg和th,如果对于任意的j,mj(tg)>mj(th),记为tg≻≻th,读为tg恒优于th。
定义2:对于聚类中心点集合T中的任意两个元素tg和th,如果对于任意的j,mj(tg)<mj(th),记为tg≺≺th,读为tg恒劣于th。
定义3:对于聚类中心点集合T中的任意两个元素tg和th,如果对于任意的j,mj(tg)=mj(th),记为tg≅th,读为tg恒等于th。
因为三种恒关系的存在,任何决策者在给两者进行决策时都会按照恒关系进行决策处理,所以就失去了对比的意义,在本文常对恒关系产生的约束条件进行约简处理,来提升优化计算效率。
3.3 距离假定
为了便于阐述,我们基于定义理想点a+(a-类似,后面不做详细阐述),对于每一个cj∈C,定义cj的标准化因子为
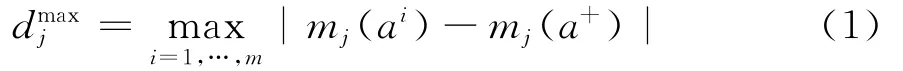
这里|x|表示x∈R的绝对值。
那么对于每一个ai∈A,ai与a+在cj上的标准化距离为:
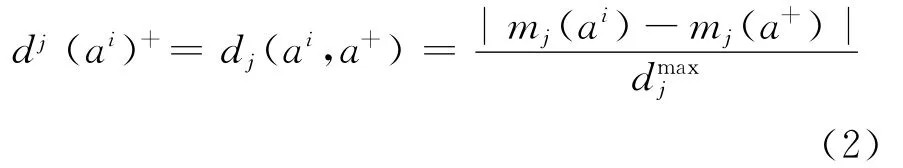
给出权重向量w,结合ai到a+在cj上的距离,给出基于p范式的加权距离定义:
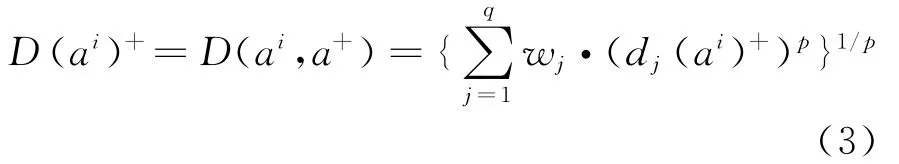
这里,实数p(p>0)是用于表示决策者偏好的一种距离测度。当p≥1时,p范式是一个凸集,大多数的研究是基于凸集的研究,特别地,当p=1时,p范式为曼哈顿距离,当p=2时,p范式为欧几里得距离,两者都具有清晰的几何意义,决策者很容易理解,为方便理解,一般p的取值为正整数。
因为D(ai)+表示该方案到理想点的加权距离,所以,D(ai)+越小,方案ai就越优。相反,也可以用负理想点来测量其距离,D(ai)-越小,方案ai就越劣。
要想利用上面的公式对备选方案集排序,必须先确定权重向量w,下面我们设计一个优化程序从决策者排序的样本集中求出权重向量。
3.4 模型构建
正如上面讨论的,wj是评价指标cj的重要度量。我们来说明怎样设计一个优化程序从决策者排序的样本集中求出权重向量w。
聚类中心点集合T中列出了他们的偏好递减序列。一般来说,如果1≤g≺h≤m,那么决策者认为tg优于th,(tg≻th)或者决策者认为tg跟th同样好,(tg~th)。因此我们做如下假定:如果tg≻th,那么tg到a+的距离小于th到a+的距离,因此D(tg)+-D(th)++≺0,或者:
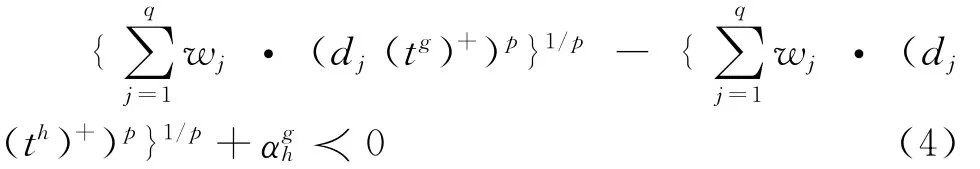
如果tg~th,那么tg到a+的距离约等于th到a+的距离,因此D(tg)+-D(th)++=0或者:
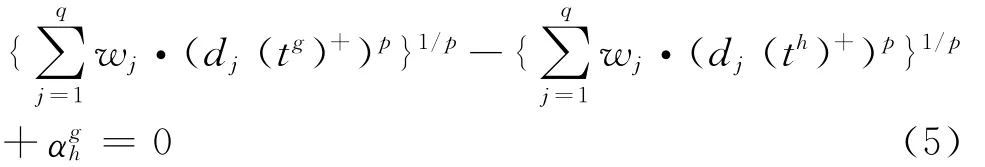
这里,∈[-1,1]是一个误差调整参数。
样本集中的所有方案都必须进行两两比较,一共需要构建(m2)个约束条件,因此,权重向量w的整体误差是:

下面的算法是根据式(6)生成的一个寻找最理想的权重向量w方法。

求解该数学模型,可得到p值、最理想的权重向量w*和最小的总体误差ERR*。
由定理1可知,对于最理想解,w*确定,p值确定,理想点确定,所以D(tg)+和D(th)+确定。由此可知,重新聚合后的结果会保持跟原排序一致。
4 应用案例分析
4.1 背景介绍
文献[8]从三个维度17个因素研究了研究生创新能力影响因素。通过网络平台的问卷调研,得到南京市4所研究型大学研究生的共247份有效问卷,问卷采用李克特5点量表法,即1=“很不符合”、2=“有些不符合”、3=“中等”、4=“有些符合”、5=“很符合”,要求被试者按照与自己的实际的符合程度打分。为了演算本文提出模型,选取其中针对创新能力评价的八个指标(如图4所示)。
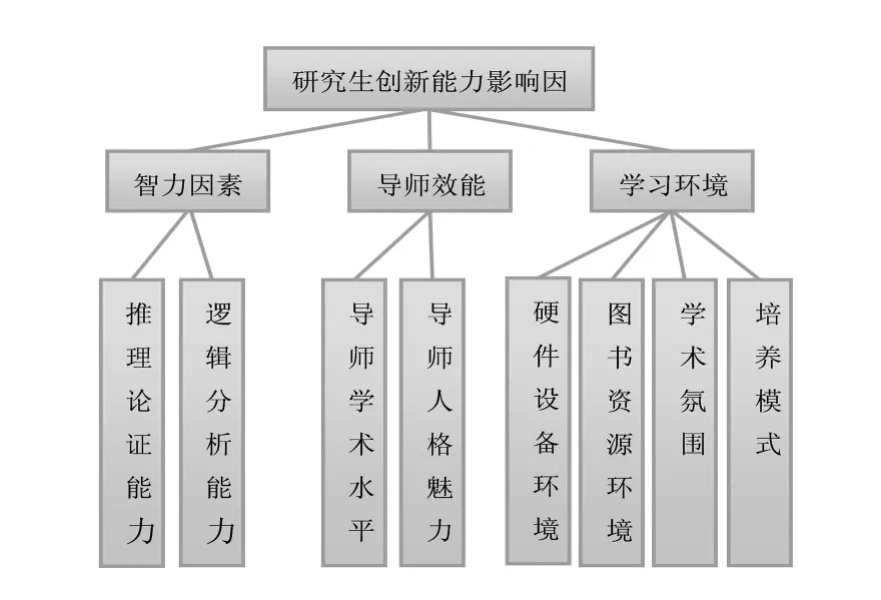
图4 八种影响研究生创新能力的因素指标
4.2 k-均值聚类
应用k-均值方法将总体247个数据进行聚类处理,在选取典型样本个数方面,如果选取的数量太少,会产生研究不全面,结果偏离比较大的不利影响,如果选取的数量太多,又会导致专家决策难度加大,计算复杂等不利影响。这里我们根据7加减2原则设定k=7,即选取7个典型样本,具体计算过程省略。表1为聚类的结果。
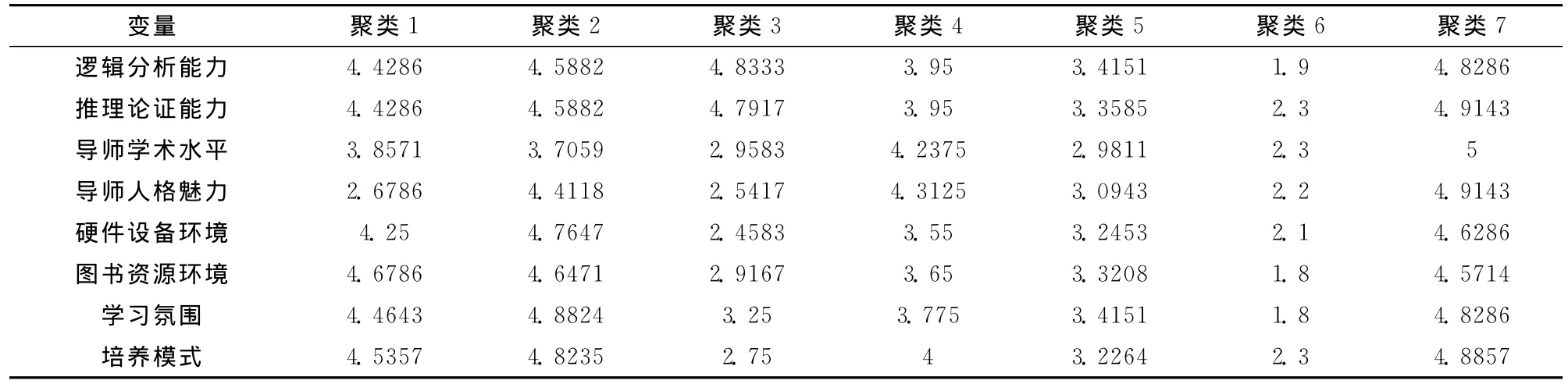
表1 聚类分析结果表
4.3 基于案例距离的优化
(1)专家对聚类排序
专家根据聚类的结果,给出如下排序:
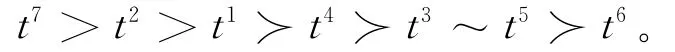
对专家的排序进行帕累托约简处理,由上表中数据可知,存在以下10个恒关系:t7≻≻t6,t2≻≻t6,t1≻≻t6,t4≻≻t6,t3≻≻t6,t5≻≻t6,t4≻≻t5,t7≻≻t5,t7≻≻t4,t2≻≻t5,故以上偏好比较关系由于是恒满足关系,无论什么形式的距离定义,因此可以在总体两两距离比较约束条件中去除。
(2)统一量纲
因为调查数据采用李克特5点量表法,数据中的最大值为5,并且因为数据量相对较大,所以取原始数据的最大值点(5,5,5,5,5,5,5,5)为理想点。同理,负理想点为(1,1,1,1,1,1,1)。
(3)理想点距离
根据理想点的具体数值,计算各聚类样本中心点的距离,如表2所示,负理想点距离的运算类似,在此不再列出。
(4)构建最优化决策模型
根据专家排序和帕累托约简的结果构建最优化决策模型,包括11个比较关系和一些变量约束条件。具体模型如下:
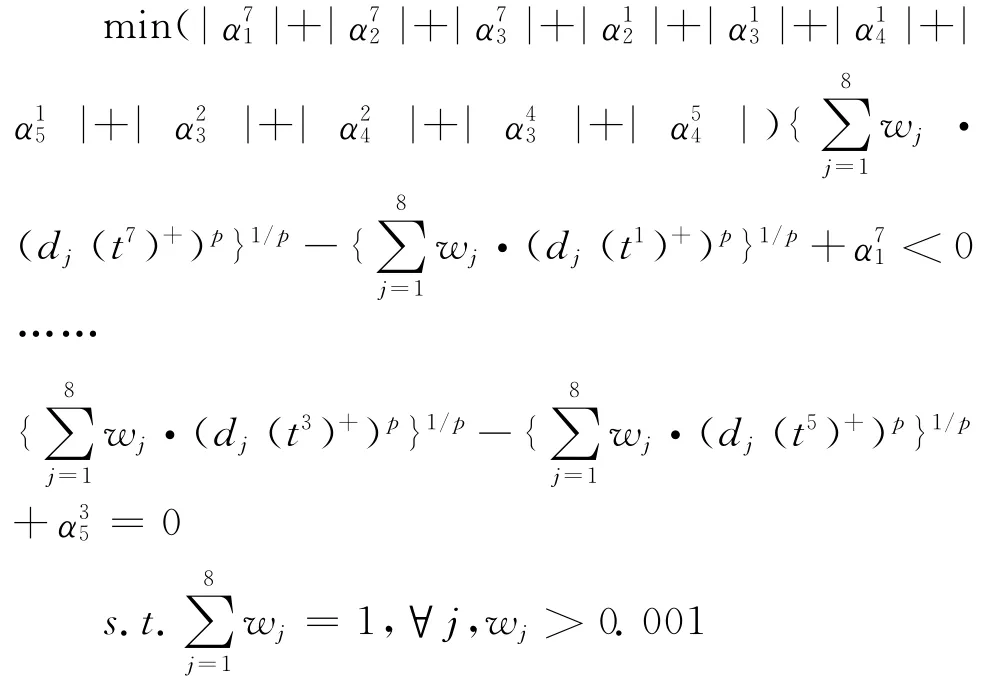
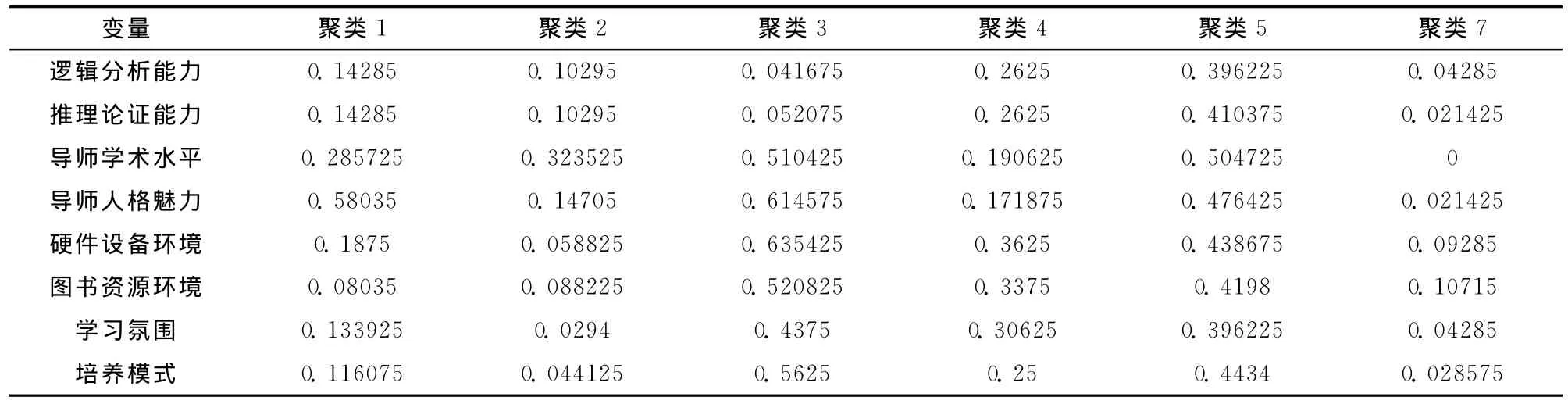
表2 理想点距离数值表
(5)求解权重
运用lingo11.0软件进行计算,得到p值和权重的解:p=2,w1=0.1560946,w2=0.1562547,w3= 0.1431026,w4= 0.1460946,w5=0.1294902,w6=0.1331026,w7=0.1331026,w8=0.0027581。
4 决策结果
(1)集结值:将247个调查数据以及所求得p值、权重值代入到前述构建的最优化决策模型中,得到247个集结值,值越小,表示距离理想点的距离越近,说明该决策值越优。为了便于比较也计算了基于负理想点的集结值(计算方法类似,不再列出),基于理想点和负理想点的集结值及其比较如图5所示。
(2)排序:根据所求集结值,可以对所有247个调查数据进行排序,排序时,基于理想点的计算,集结值越小,决策值越优,相反,基于负理想点的计算,集结值越大,决策值越优,由于篇幅原因,具体排序结果在此不一一列出。
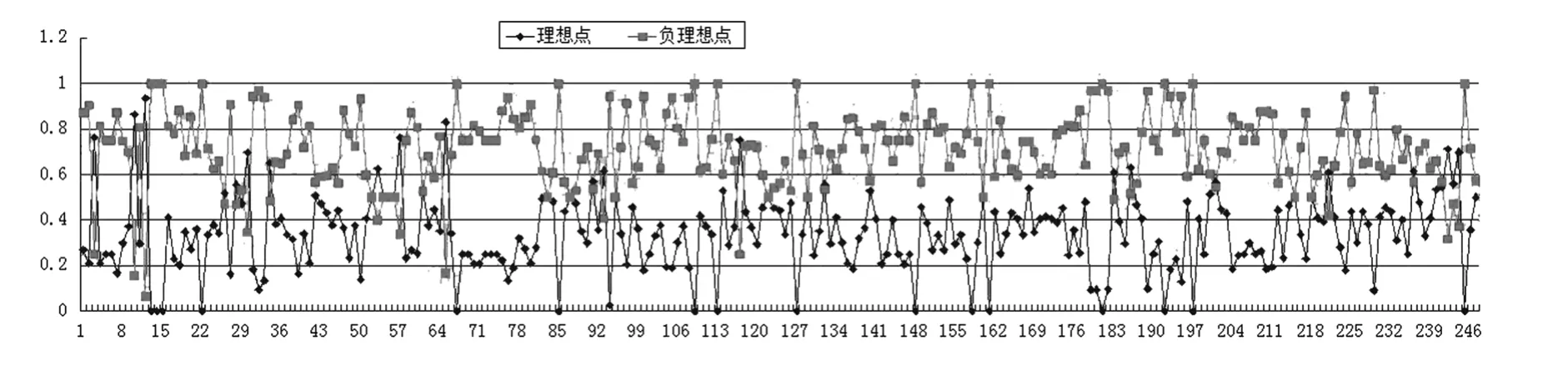
图5 基于理想点和负理想点的集结值及其比较
5 结语
本文针对数据量较大的多属性决策问题,在以前研究的基础上,采用聚类分析和案例距离相结合的方法,先将数据进行聚类处理,用案例距离法对几个聚类中心点进行最优化建模处理,得到相应关键参数,再将原始数据和所得参数套入最优化模型,得到具体集结值,由此可以进行选优、排序、分类等决策处理。最后用研究生创新能力评价的案例说明了其可用性。
[1]Roy B.Multicriteria methodology for decision aiding[M].Dordrecht:Kluwer,1996.
[2]刘佳鹏,廖貅武,蔡付龄 .基于案例比较信息的多准则群决策分类方法[J].系统工程理论与实贱,2014,34(4):971-980.
[3]蔡付龄,廖貅武,杨娜 .基于案例信息的多准则群决策分类方法[J].管理科学学报,2013,16(2):22-32.
[4]Jacquet-Lagreze E,Siskos Y.Assessing a set of additive utility functions for multicriteria decision-making:The UTA method[J].European Journal of Operational Research,1982,10(2):151-164.
[5]Chen Ye,Kilgour D M,Hipel K W.Multiple criteria sorting u-sing case-based distance models with an application in water resources management[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A,2007,37(5):680-691.
[6]Slowinski R.Rough set theory for multicriteria decision analysis[J].European Journal of Operational Research,2001,129(1):1-47.
[7]Mousseau V,Slowinski R.Inferring an ELECTRE TRI model from assignment examples[J].Journal of Global Optimization,1998,12(2):157-174.
[8]李遥,陈晔,廖勇,等 .一种多属性主客观对比评价模型及应用[J].南京航空航天大学学报,2015,47(1):104-112.
[9]Chen Ye,Kilgour D M,Hipel K W.A case-based distance method for screening in multiple-criteria decision aid[J].Omega,2008,36(3):373-383.
[10]Chen Ye,Li K W,Kilgour D M,Hipel K W.A case-based distance model for multiple criteria ABC analysis[J].Computers and Operations Research,2008,35(3):776-796.
[11]蔡付龄,廖貅武 .案例信息不确定下的多属性分类方法[J].系统工程理论与实践,2010,30(3):513-519.
[12]王翯华,朱建军,方志耕 .基于案例分析的语言信息灰靶决策分类模型[J].系统工程理论与实践,2013,33(12):3172-3181.
[13]王坚强,高阳,吴小月,等 .信息不完全确定的区域产品模糊区间聚类方法[J].中国管理科学,2006,14(3):80-85.
