基于局部路网空间结构特征的无检测器路段交通流预测方法*

叶秀秀 马晓凤▲ 钟 鸣 黄传明

（1.武汉理工大学智能交通系统研究中心 武汉430063；2.武汉理工大学国家水运安全工程技术研究中心 武汉430063；3.武汉市公安局交通管理局 武汉430030）

0 引 言

短时交通预测是城市智能交通系统的重要部分，能为出行者提供出行路径参考，也可为交通管理者制定交通控制和交通诱导决策提供依据。目前，短时交通流预测理论研究已经相对成熟，预测模型主要分为：①基于统计方法的模型，如历史平均法[1]、时间序列模型[2]等；②基于非线性系统理论的方法，如小波理论模型[3]等；③人工智能算法，近年来相关学者多使用该类方法进行交通流预测研究，如Chen等[4]针对交通流具有时变和非线性的特点提出改进的小波神经网络短时交通流预测模型，其预测误差比传统的小波神经网络减小了14.994%；冯微等[5]基于深度学习构建短时交通流参数预测模型，实现对大规模路网速度参数预测；④多种算法组合应用，如Asif Raza等[6]采用遗传算法对人工神经网络进行优化并结合局部加权回归进行短时交通流预测。以上方法主要为基于单个路段的交通流特性对该路段进行交通流预测研究。为提高预测精度及更全面的挖掘交通流变化规律，许多学者进行了基于路网时空特性的交通流预测研究，如李巧茹等[7]针对交通流量时间序列具有混沌特性进行相空间重构，并在此基础上构建PSO-GPR模型短时交通流预测模型；Alireza Ermagun等[8]基于路网交通流数据提取路网的网络权值矩阵进行短时交通流预测，该权值矩阵在交通流预测精度高于传统的空间相关性方法且具有随时间变化的稳定性和鲁棒性。

上述交通流预测方法是基于目标路段及相关路段历史交通流进行模型训练，适用于有检测器路段。但是随着城镇化及城市路网的快速扩张，检测器难以覆盖路网的所有路段，如武汉市路网空间化后有ID的路段共有5万多条，其中有检测器的路段只占10.48%。因此,要实现路网的宏观管理，无检测器路段的交通流预测将是路网交通流预测不可缺少的一部分。但是，国内外对于无检测器路段交通流预测理论研究还处于发展阶段。张赫等[9]利用交叉口的相关性采用聚类分析、逐步回归分析及主成分分析分别进行无检测器路段的交通流预测，其中主成分分析法计算工作量大于另外2种方法，该方法能够包含的交通信息量更多并且预测精度更高，其中聚类分析和主成分分析是早期研究中应用较多的方法[10-11]。基于灰色预测模型（GM）预测所需原始数据少的特点，相关学者采用改进的GM、GM与神经网络的组合算法（GNN）等方法，以路段观测数据进行模型训练和交通流量预测，基于目标路段观测数据的改进GM算法和GNN算法，其预测平均相对误差可减小2%～10%[12-13]。此外，王志建[14]利用遗传算法改进的逐步回归分析法进行无检测器交叉口流量预测，相对于早期聚类分析法和主成分分析法，该方法对无检测器路段流量预测平均相对误差减小了11%和6%；郭沂鑫[15]首次将PNN概率神经网络应用在无检测器交叉口的归类中，实验结果显示PNN分类模式预测模型具有一定的稳定性，优于传统的分类方法。由于交通流量具有不确定性和复杂性等特点，数学解析的硬分类模型在解决交通流问题中存在局限性，对此张明辉[16]提出采用模糊C均值（FCM）聚类方法对城市路网中各个交叉口进行模糊聚类，基于该方法进行无检测器路段的短时交通流预测易于实现且预测精度较高。

以上利用路段聚类、回归分析等统计方法及人工智能算法对无检测器路段进行交通流预测研究中，仍需要一定数量的无检测器路段历史数据进行模型训练，这些历史数据一般来源于浮动车数据及人工采集等，采集手段有限，且存在采集精度差、成本高、实时性差等不足。因此，需要发掘新的方法以解决大量无检测器路段的交通流预测问题，这样才能在大规模全路网的快速预测和应用中具有可操作性和实用性。笔者提出1种基于上游路段空间特征影响度系数的交通流预测方法，对路网中所有路段均有检测器的交叉口进行数据挖掘和规律分析，获取路段空间特征影响度系数。然后选取无检测器路段为案例研究对象，基于空间特征影响度系数、案例空间特征及其上游路段交通流量，进行该案例的流量预测计算及验证。

1 路段空间特征与交通流的相关性分析

城市道路交通是1个复杂的系统，交通流受多种因素的影响，表现出非线性、不确定性等特性。由于道路之间相互连通，上下游交通状态之间的具有一定的相关性，该相关性可以使用上下游的流量关系来表示。

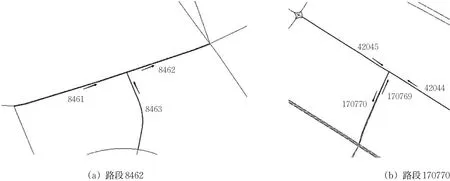
图1 交叉口路段空间关系示意图Fig.1 Spatial relationship between intersections

图1 为武汉市路网2个交叉口上下游空间示意图。其中，次干道8462路段的上游有8461和8463这2个路段，二者分别为次干道及支路；次干道170770的上游路段为170769、42045及42044，其中，170769为次干道，4045及42044路段则是支路。路段8462、170770及其上游2019年2月15日的交通流情况见图2。

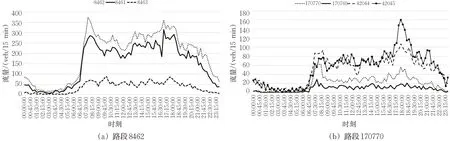
图2 上下游路段交通流关系示例Fig.2 Cases of the traffic flow relationship between upstream and downstream roads

从图2中可看出，在上下游的流量关系中，不同道路类型的路段流量变化情况具有一定的差异，道路类型相同的路段其交通流变化趋势相似，且上游路段数量对下游路段交通流也会有一定的影响。

为明确空间特征对路段交通流量是否具有相关性，本文基于武汉市路网信息数据获取以下3个空间特征。

1）路段道路类型，分为快速路、主干道、次干道、快速路辅路及支路，属于分类变量。为简化建模数量、提升计算速度，根据道路等级、功能及宽度等因素，本研究将高速路和快捷路划分为快速路，辅路划分为快速路辅路，匝道及转向专用道划分为支路。其中快速路路段共239个，主干道路段共391个，次干道路段共621个，快速路辅路路段共143，支路路段共890个。

2）相邻路段数量，相邻上游路段数量或下游路段数量，属于数值变量。

3）相邻路段道路类型，相邻上游或下游路段的道路类型，划分方法同1）。

交通高峰期时路段拥堵显著、路段交通流变化规律性强，针对武汉市2 285个卡口检测器早高峰交通流量数据及对应的空间特征数据，利用SPSS进行Spearman相关性分析，结果见表1。由表1相关性分析结果可知：路段流量与路段道路类型、相邻路段数量及相邻路段道路类型3类空间特征均呈现显著性相关，其中路段流量与路段道路类型的相关性最大；相邻路段空间特征与路段流量的相关性中，相邻上游路段特征与流量间的相关系数大于下游路段。

由此，考虑从路段道路类型及相邻路段数等空间特征出发，挖掘路网中有检测器路段的空间特征对交通流分配的影响度，利用无检测器路段相邻路段的交通流数据及空间特征影响度系数，进行无检测器路段交通流预测。

表1 路段特征与流量的相关性分析Tab.1 Correlation analysis of road characteristics and traffic flow

2 路段空间特征影响度预测模型

2.1 基于路网拓扑的交通流分配权重模型

交叉口上下游各个路段间的交通流存在着一定的分/合流关系，交叉口中目标路段的交通流量y与其n个上游路段（或下游路段）的流量x1，x2，…，x n间的流量分配权重模型[17-18]为

式中：y为目标路段交通流量，veh/15 min；x1，x2，…，x n为n个上游（或下游）的交通流量，veh/15 min；θ0，θ1，θ2，…，θn为交通流权重系数。

令θ为n+1的列向量，见式（2）。令X b为（m，n+1）的矩阵；n为自变量个数；m为训练样本，见式（3）。

目前，在回归分析中参数估计应用最多的算法是最小二乘法，该方法是以误差的平方和最小为准则，依据观测数据估计线性模型中未知参数的1种基本参数估计方法。基于路网拓扑交通流数据，采用最小二乘法求解交通流分配权重，结果见式（4）。

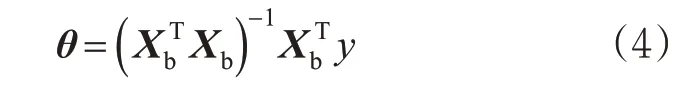
求出向量θ，即模型的具体回归系数，基于路网拓扑的交通流分配权重模型求解完成。

2.2 路段空间特征影响度系数预测模型

以往研究无检测器路段交通流未来变化规律的成果中，一般先通过临时布点采集交通流数据，再构建预测模型进行预测[17,19-20]，适用于对单一或若干道路开展研究。但是由于城市内无检测器路段数量大、分布广，如武汉市近90%的路段为无检测器路段或检测器失效路段，要在小时间粒度条件下获取大量无检测器路段的交通流样本数据十分困难，导致无检测器路段因缺少历史数据不能开展交通流分配权重模型的训练。

从表1的相关性分析结果可知，交叉口上下游路段的交通流分配系数是路段道路类型、上游路段数量等多个空间特征综合作用的结果，即每个交通流分配系数与多个空间特征变量之间存在一定的相关性。本文在大量有检测器的交叉口路段交通流分配权重模型训练结果的基础上，再次采用多元线性回归方法深入挖掘空间特征对交通流分配权重的影响规律，提取路段空间特征对交通流分配权重的影响度系数。进而基于该影响度系数、目标无检测器路段的空间特征以及相邻路段交通流数据，可实现无检测器路段短时交通流预测。该预测方法从城市路网中有检测器交叉口的海量数据中挖掘路段空间特征对交通流分配权重的影响度系数，在模型训练及目标无检测器路段交通流预测过程中无需将目标路段的历史数据作为输入，能够实现城市大规模路网中大量无检测器路段交通流的快速、实时及准确预测。

对某一无检测器路段，若其所有上游路段或者下游路段均有检测器数据，此方法能够有效地对该路段进行交通流预测。本文针对无检测器路段所有上游都有检测器数据的情况进行建模，其他情况可参照该方法进行，其模型步骤如下。

1）路网有检测器路段回归方程训练。

基于交叉口上下游各个路段间的交通流的分/合流关系，交叉口中单个路段的交通流量y与其n个上游路段（或下游路段）的流量x1，x2，…，xn间的交通流分配权重可根据历史交通流数据采用2.1中路网拓扑的交通流分配权重模型求出。对路网中路段本身及其上游均有检测器的路段进行统计（k个），采用多元线性回归算法分别对k个路段及其上游的历史交通流数据进行回归分析，可以获得各路段与其上游路段的交通流分配权重方程。

式中：y j为第j个路段流量，veh/15 min；X j为其上游路段的流量组成的向量；θj为回归方程的参数向量（j=1，2，…，k）。

2）空间特征影响度系数回归分析。在1）的基础上，再次利用多元线性回归对空间特征和交通流分配权重进行回归分析，研究空间特征对交叉口交通流分配权重的影响度系数。在式（5）交通流分配权重计算结果中，以k个回归方程的交通流回归参数向量及对应路段的空间特征为训练样本，进一步挖掘路段空间特征对交通流分配权重的影响度规律。其详细过程为将目标路段道路类型f1、上游道路数量f2及上游路段的道路类型f3作为自变量，对回归方程回归系数向量θ中的常数项θ0及偏回归参数θi分别作为因变量，进行多元线性回归分析。构建空间特征与交通流权重参数间的回归方程过程中，需要综合考虑目标路段道路类型、上游路段数量及上游路段道路类型3项空间特征对交通流分配权重的影响。θ0作为交通流分配权重模型的常数项，其回归方程构建应同时考虑前2项空间特征以及所有上游道路类型的影响；θi作为交通流分配权重模型的偏回归参数，前2项空间特征与该参数对应的上游道路类型为主要影响因素，即常数项的及偏回归参数回归方程，见式（6）。

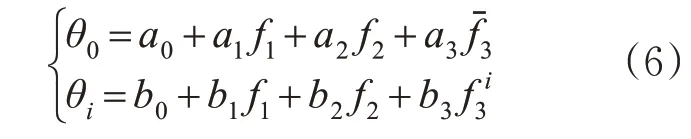
式中：θ0为路段回归方程的常数项；θi为路段回归预测方程中第i个上游路段对应的偏回归参数为第i个上游路段的道路类型为n个上游的道路类型综合值。

根据式（5）中各个路段交通流分配权重回归模型及其对应的空间特征求解式（6），获得上游空间特征影响度向量见式（7）和式（8）。

其中：A为空间特征对预测方程常数项θ0的影响度向量；B为偏回归参数θi的空间特征影响度系数向量。

3）基于空间特征影响度系数的交通流预测。通过向量A和B可求出无检测器路段上游流量分配权重向量θ，再结合上游各路段交通流X就能对目标路段交通流y进行预测。如，对于具有单个上游的无检测器路段，空间特征分别为目标路段道路类型f1、上游道路数量f2及上游路段的道路类型f3，则其交通流预测方程为

对于具有2个上游的无检测器路段，空间特征分别为目标路段道路类型、上游道路数量上游路段的道路类型为则其交通流预测方程为

其他情况以此类推。

3 案例分析

3.1 数据来源

数据来源于武汉市智慧决策系统，该系统对武汉市地磁检测器、卡口电警、线圈检测器共计5 869个点位、20 713个检测器进行管理。系统中路网含50 400多个路段，路段是路网中道路的有向划分单元，具有唯一的ID编号，本文选取武汉市路网中交叉口各路段均安装卡口电警检测器且检测器正常工作的共135个路段进行数据挖掘和训练，将16176、170239路段用于模型验证。其中，路段16176为主干道，位于二环线内靠近长江二桥，其上游只有1个主干道路段16176；路段170239为次干道，位于三环线外，离主城区较远，具有4个上游路段170217、170238、170240、170273，前2个的道路类型为次干道，后2个为支路。

案例中使用的交通流数据以15 min的数据增量周期为1个时段，利用箱型图法对所选路段2019年2月14日—3月3日的交通流数据进行分时段的交通流阈值计算，在此基础上进行数据清洗并利用历史平均法进行数据填补。路段空间特征数据为智慧决策系统空间化信息提取结果，其中路段道路类型分为辅路、支路、次干道、主干道、快速路及高速路6类，将其分别赋予编号1～6。

3.2 预测结果和分析

由于城市路网交通流具有明显的时变特征，不同时间段流量变化规律不同，选取07：00—09：00的早高峰数据进行研究，其他时段可参照此流程进行。利用多元线性回归算法对训练数据进行回归计算，获得68组上下游交通流分配权重，并基于权重数据和路段空间特征数据进行回归分析，计算空间特征影响度系数。最终获得空间特征影响度系数向量分别为

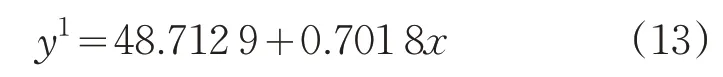
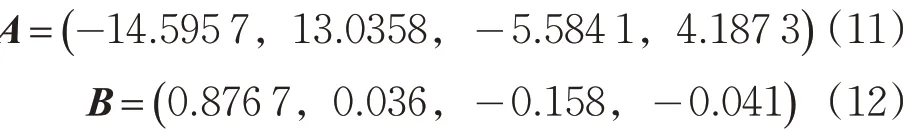
利用以上方程及上游路段交通流量分别对16176及170239路段进行交通流预测计算。

针对2019年2月14日3月3日每天上午07：00—09：00共161个时段进行交通流预测验证，图3为16176及170239路段实际交通流量与基于空间特征影响度系数预测的交通流对比情况，其预测的交通流与实际交通流变化趋势相近。

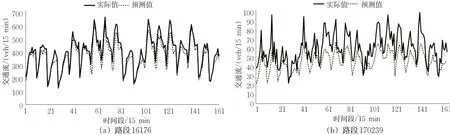
图3 路段交通流实际值与预测值对比Fig.3 Comparison of actual and predicted traffic flow of roads

采用绝对百分比误差（absolute percentage error,APE）对路段空间特征影响度系数模型进行预测性能评价，见式（15）。

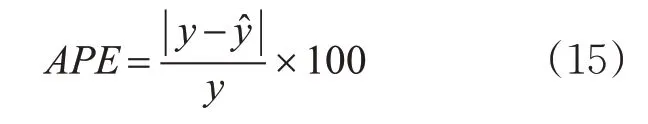
式中：y为实际流量值，veh/15 min；ŷ为预测流量值，veh/15 min。

由模型得到的预测结果绝对百分比误差曲线见图4，可以看出：本文所提出的路段空间特征影响度系数模型在不需要预测目标路段历史交通流的情况下，以路段的空间特征及上游路段交通流量数据作为预测因子，得到单个上游的路段预测结果绝对百分比误差曲线波动情况稳定，对于多个上游的路段预测结果绝对百分比误差曲线波动的幅度较大。

图4 交通流预测绝对百分比误差Fig.4 APE of traffic flow prediction

路段16176和170239预测APE进行平均值及百分位值的统计，结果见表2，其中，PR表示百分位数值，表示在此样本值以下的样本数占总样本数的百分比。对主城区的主干道路段16176的预测平均误差为8.96%，对非主城区的次干道路段170239的预测平均误差为22.82%，预测效果较好。

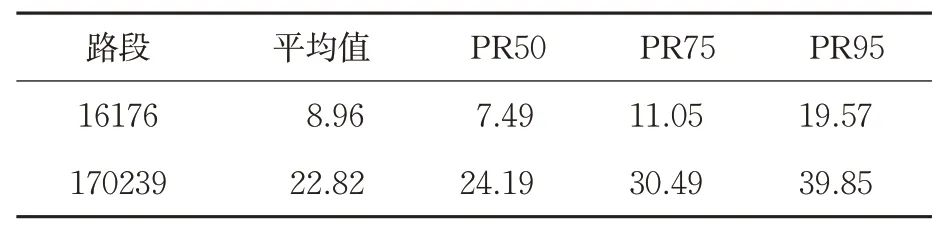
表2 预测绝对百分比误差统计Tab.2 Statistics of forecasted APE%

4 讨 论

本次研究是基于路网有检测器路段数据进行数据挖掘，研究目标路段道路类型、上游的路段数量及其道路类型等空间特征对交通流分配权重的影响，数据源为武汉市卡口电警检测器的流量数据。以下对本文提出的模型及案例中造成误差的原因进行分析。

1）由课题组调研数据可知，目前武汉市卡口电警数量超过检测器总数的50%，且44%左右的卡口电警没有数据记录，而有过车记录数占总记录的比例大于0.5的只有30%左右。本文获取的卡口电警数据源存在部分数据异常及数据缺失问题，在进行数据预处理过程中，采用箱型图法和历史平均法进行数据清洗，且清洗数量较大。经过数据清洗后，能够增加可用数据样本，但是清洗数据与实际数据不可避免地存在误差，对模型训练精度有一定的影响。

另外，本文在训练数据的选取上，需要选取上下游均有卡口检测器且具有大量的历史数据的路段数据作为训练样本，在现有检测器完好率的情况下，满足筛选条件的相对较少，使得模型在数据挖掘过程中样本数据覆盖不够全面，对模型精度产生不利影响。在后续研究中可以通过增加训练集样本、增大样本在路网中的覆盖度来提高模型的准确度。具体措施为将多种检测器数据融合结果作为训练集；对模型进行改善，再将只有部分上游或下游路段有数据的情况归入训练集。

2）对路段交通流有影响的空间影响因素较多，本文目前只对目标路段道路类型、上游的路段数量及其道路类型3种空间特征进行研究，未考虑路段所处的地形、土地利用类型等因素的影响，特征影响度在未来研究中仍可进一步完善和提高。

另外，对训练样本数据进行空间分析发现，满足训练标准的数据主要来源于主城区且布设检测器较多的密集路网区域，因此对非主城区路段预测时其误差会相较于主城区路段大。如案例研究中的170239路段，其离主城区较远，且其为交通量不大的次干道，所以预测结果APE较大，预测效果明显次于16176路段。

3）现有无检测器路段交通流预测研究中主要分为基于无检测器路段自身历史交通流及路网中相关路段交通流2类数据进行无检测器路段流量预测，这些研究主要针对路段交通流变化规律进行研究，未考虑路段空间时不变特征对路段流量产生的影响。本文基于第2类数据，在大量有检测器交叉口交通流分配权重基础上，进一步深入挖掘道路类型及相邻路段的数量等空间特征对交通流分配权重的影响规律，进而将大量有检测器数据获取的规律应用于无检测器路段进行交通流预测。

另外，目前主流的无检测器路段预测方法需要将一定数量的无检测器路段流量数据作为训练数据，但目前大部分城市路网中无检测器路段占比在90%左右，对无检测器路段进行交通流采样不仅耗费大量时间和人力，同时也难以满足城市路段交通流预测实时性的需求。本文通过研究路段空间时不变特征对交叉口交通流分配权重的影响度系数，实现在不需要无检测器路段交通流数据作为训练数据的情况下，将从海量有检测器路段挖掘的规律应用至无检测器路段，从而实现城市大规模路网中大量无检测器路段快速、准确的预测。

5 结束语

路网短时交通流预测对城市交通控制、诱导及居民出行至关重要，现阶段无检测器路段在城市路网中仍占有很大的比重，且其历史数据难以获取，因此对无检测器路段交通流预测进行研究具有十分重要的意义。针对此问题，笔者在现有研究基础上，研究路段空间特征对交通流分配的影响度系数，并基于此进行无检测器路段交通流预测。针对武汉市上下游均有卡口电警检测器的交叉口数据进行数据筛选和分析，在采用多元回归获得上游路段交通流分配权重基础上，再次利用多元线性回归对路段空间特征和交通流分配权重进行分析，得出空间特征权重的影响度系数，最后结合路段空间特征及上游交通流进行无检测器路段交通流预测。

案例结果表明，所提出的方法能够在不需要无检测器路段历史数据的情况下，基于路段空间特征及上游路段交通流即可对下游无检测器路段的交通流预测进行预测，能够为交通管理者制定交通决策提供一定的参考。