沪南公路跨线桥抖振响应数值分析研究

傅 梅，陆元春，孙梦瑾

[上海市城市建设设计研究总院（集团）有限公司，上海市200125；2.同济大学 土木工程学院桥梁工程系，上海市200092]

0 引言

随着桥梁结构跨径的不断增加，风与结构的相互作用以及由此引发的桥梁结构安全性与舒适性问题也越来越显著[1]。另一方面，计算流体动力学理论的不断发展成熟，使得基于虚拟风洞技术的结构风荷载确定及抗风性能分析越来越受到国内外学者的广泛关注，并在大量桥梁工程中得到了实际推广和应用[2]。

抖振是桥梁结构在脉动风激励下的一类典型限幅振动形式，虽然抖振不会对桥梁结构的安全产生威胁，但过大的振幅及加速度容易造成严重的行车及行人舒适性问题，并对局部构件的疲劳性能产生一定影响[3]。因此，抖振荷载下的响应分析仍是桥梁结构抗风性能分析的重要组成部分。

国内外大量学者针对桥梁结构的风荷载特性及抖振性能开展了一系列分析。徐欣等对中欧规范中的桥梁结构风荷载计算方法采用算例分析的方式进行了详细对比[4]。郑亮等[5]采用CFD模拟方法对复杂造型桥塔的横桥向和顺桥向风荷载进行了系统研究。Chen等通过考虑振动模态的气动耦合效应分析了某桥梁的抖振响应[6]。张志田等[7]提出了基于准定常气动刚度与基于试验的非定常气动阻尼进行气动修正的大跨度桥梁抖振计算新模型，并以东海大桥为工程背景进行了案例分析应用。胡涛等[8]对平潭海峡元洪航道主桥在施工阶段的抖振响应开展了研究，并系统揭示了最大单悬臂状态与最大双悬臂状态下的抖振响应差异。

本文依据《公路桥梁抗风设计规范》（JTG/T 3360-01—2018）[9]中对风荷载的相关定义，基于虚拟风洞技术对沪南公路跨线桥的静气动力系数进行了模拟，并进一步对其抖振荷载下的结构响应进行了分析。本文研究方法及结论对国内类似桥梁工程的抗风设计具有参考意义。

1 工程背景

沪南公路是有着悠久历史的干线公路，其改扩建项目建成后，将极大地缓解周围区域居民的出行压力。沪南路高架跨线桥西起秀沈路交叉段，东至康花路交叉段，设计荷载为城—A级，是沪南路（康花路~上南路）改建工程的重要组成部分。其中，K20上部结构采用简支钢混组合小箱梁，梁高1.9m。K27(跨秀康路)，K46(跨康桥路)上部结构采用简支钢-混凝土组合梁，钢梁结构高2.5m，桥面板厚0.25m。在跨越S20主线桥梁时采用变截面连续钢箱梁，跨径布置为（80+120+110+80.5）m，总长390.5m，变截面钢箱梁梁高h=3~6m，梁宽17.2m。其余均采用简支、桥面连续组合小箱梁，梁高1.6m。

沪南路跨越S20主线桥梁段的高架跨线桥立面布置图如图1所示，桥梁起始桩号为K2+853.00，平曲线起始桩号为K3+053，圆曲线半径为1000m。竖曲线分为两段，一段从起始端到跨中支点处，纵坡为3%，另一段从中支点到结束端，纵坡为2.75%。

沪南路跨越S20主线桥梁段的高架跨线桥采用变截面连续钢箱梁，在国内采用全钢结构的变截面连续钢箱梁桥比较少见，该类桥梁主要特点是结构阻尼比较低，对风的作用较为敏感，加上桥梁处台风影响区，易受大风天气影响。因此，针对该桥开展风荷载特性研究及抖振响应分析是十分必要的。

图1 沪南公路跨线桥立面布置图

2 风参数与动力特性分析

2.1 风参数确定

根据《公路桥梁抗风设计规范》（JTG/T3360-01—2018）中的全国基本风速分布图和全国各气象台站的基本风速值，结合沪南公路跨线桥桥位处的基本信息，参照规范附录A中的规定，标准高度10m、平均时距10min、重现期100a的基本风速定为32.8m/s，并由此确定该桥抗风风险区域为R1等级。根据基本风速，计算得到设计基准风速为40.4m/s。

2.2 结构动力特性

采用三维有限元分析软件对该模型进行结构动力特性分析。主梁采用梁单元模型建立全桥结构三维有限元模型如图2所示。图中横桥向的鱼骨梁仅为振型分析所需，对结构静动力特性不提供任何贡献。

图2 ANSYS全桥三维模型示意图

通过模态分析得到桥梁结构的前5阶振型及频率见表1，图3给出了第1阶模态（主梁竖弯振动）以及第5阶模态（主梁部分侧弯振动）的振型图。

表1 前5阶模态分析汇总表

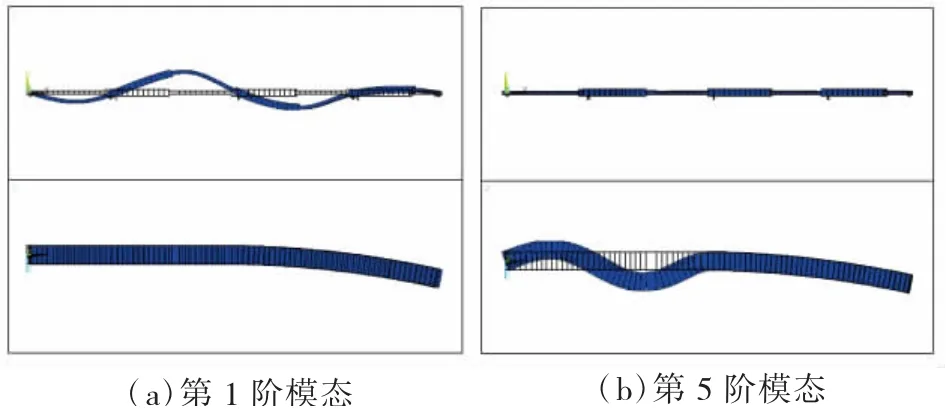
图3 桥梁结构典型振型示意图

3 静气动力系数数值模拟

基于计算流体动力学的基本理论，采用虚拟风洞技术求解主梁典型断面的静气动力系数。该研究采用基于时间平均的雷诺均值Navier-Stokes方程（RANS）模型中使用最广泛的Realizable双方程湍流模型，相关计算方法及计算参数见表2，主跨跨中位置处的虚拟风洞断面布置图，如图4所示。

表2 计算方法及参数列表

图4 主跨跨中位置断面布置示意图

通过虚拟风洞技术可获得主梁断面在体轴坐标系下的气动阻力系数、升力系数和力矩系数三个分量，考虑0°、±3°三种不同的风攻角，进而可通过坐标转换求得其在风轴坐标系下对应的静气动力系数。以风轴坐标系为例，图4中跨中断面的静气动力系数计算结果见表3。图5以0°风攻角为例，给出了断面周围流场的模拟效果。

表3 主跨跨中断面静气动力系数计算汇总

其余典型断面的分析方法与上述理论类似，在此不再赘述。

4 抖振响应分析

4.1 脉动风场模拟

结构抖振响应分析的第一步是得到脉动风的时程特性，该特性可通过风观测站的实测数据获得，缺乏可靠数据时也可通过数值模拟的方法获取。本研究采用谐波谱解法模拟随机脉动风场，该方法理论完善，其样本的各态历经特性已得到严格的数学证明并在众多工程案例中得到广泛应用，模拟结果较为可靠。模拟中所采用的风场为B类风场，并以设计基准风速为平均风速。

如图4所示断面位置，模拟得到的时程总长t=150s，时间步长为0.05s的横桥向脉动风如图6所示。

获得脉动风时程后，作用在主梁断面的脉动风荷载可按下式计算：

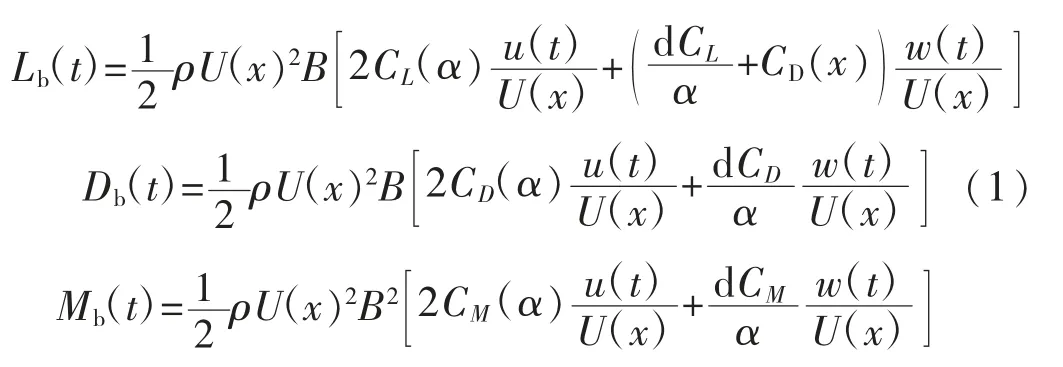
式中：Lb（t）、Db（t）分别为竖向时程力和横向时程力，N；Mb（t）为时程力矩，N·m；ρ为空气密度，g/m3；α为风攻角，°；U（x）为顺桥向坐标x位置处的设计基准风速（即平均风效应），m/s；u（t）和w（t）分别代表不包含平均风效应的横桥向及竖向脉动风时程，m/s。

4.2 抖振响应分析结果

以图4所示断面为例，通过有限元动力瞬态分析得到的竖向及横桥向位移时程分别如图7和图8所示。

经分析得到，在4.1节得到的脉动风时程作用下，主梁结构最大竖向位移为0.24m，发生在第二跨跨中；最大横桥向位移0.016m，发生在第一跨跨中；竖向最大弯矩为1.26×108N·m，发生在第一跨支点处；横向最大弯矩为2.82×108N·m，发生在中支点处。上述响应均在结构正常使用极限状态合理范围之内。

5 结 论

本文以沪南公路跨线桥为工程背景，采用虚拟风洞技术分析了变截面连续钢箱梁的静气动力系数随风攻角变化规律，并结合获取的静气动力系数数值，通过建立全桥结构三维杆系有限元模型，分析了结构在抖振作用下的位移响应及内力响应。研究结果表明：主梁结构最大竖向位移为0.24m，最大横桥向位移0.016m，竖向最大弯矩为1.26×108N·m，横桥向最大弯矩为2.82×108N·m，桥梁结构满足正常使用极限状态下的各项安全要求。以竖向最大位移和横桥向最大弯矩为例，图9和图10分别给出了其沿顺桥向不同坐标位置的变化情况。

图9 最大竖向位移沿桥长方向变化趋势

图10 最大横桥向弯矩沿桥长方向变化趋势