自锚式悬索桥地震响应分析

谭 伟，余 振

（1.中国市政工程西南设计研究总院有限公司，四川 成都610081；2.中都工程设计有限公司，四川 成都610041）

0 引言

近年来，公路和铁路网的不断扩大，公路和铁路线路对大跨度桥梁的需求越来越大。而悬索桥是特大跨径桥梁的主要形式之一，具有跨越能力强，外观优美等特点，使得悬索桥得到了广泛使用。近几年地震频发，为确保广泛使用的悬索桥在地震作用下的安全性，对其进行抗震分析显得尤为重要[1-2]。

地震具有不可预测的特点，给桥梁带来不可逆的损伤。由于实测地震波缺乏，为充分考虑悬索桥在地震作用下的非线性动力响应规律，学者们将人工合成地震波作为悬索桥模型的地震动输入补充选择。对人工地震波的合成技术研究，学者们提出了不同的人工地震波合成方法。邢林海[3]，李江帆等[4]探讨了目标反应谱和功率谱的转换方法；张郁山等[5]研究了基于小波函数的反应谱拟合方法；谢皓宇等[6]采用连续小波变换实现地震波在时域和频域的变换。同时，刘军泉[7]分析了大跨度悬索桥的地震响应影响因素；阳威等[8]考虑了行波效应对大跨度悬索桥地震响应的影响；郭志明[9]等研究了柔性中央扣对于悬索桥的抗震性能的影响；易富等[10]研究了人工地震波作用下的悬索桥地震响应；张净霞[11]比较了反应谱法和时程分析法的悬索桥地震响应差异。

根据上述研究，现基于小波函数法，合成人工地震动时程，并对其进一步优化，使得优化处理后的人工地震动的反应谱和目标设计反应谱吻合更好。基于建立的大跨度悬索桥三维有限元模型，施加人工地震波，并进行非线性动力分析，研究了地震作用下大跨度悬索桥的动力响应规律。

1 人工合成地震波

为了合成满足该悬索桥桥址处场地土特性的人工地震波，包括频谱、幅值和持时三方面的要求。现以公路桥梁抗震设计细则（JTGTB02-01—2008）的设计反应谱(见图1)作为目标谱，生成符合目标谱特征的人工合成地震波。

图1 反应谱比较图

将反应谱转换为当量的加速度时程，需要先将反应谱转化为当量功率谱，然后由功率谱求解傅里叶幅值谱，最后使用傅里叶逆变换得到平稳的加速度时程曲线。

基于随机振动理论，假定单质点体系响应y的方差为σy，在持续的时间段t（本文中t=30s）内,不超过概率为p的最大反应yp，s可表示为[12]：

式中：rp，s为峰值系数。

本文使用Vanmarcke方法[13-14]，假定输入的功率谱在较宽的频带上平缓变化并且系统的阻尼（ξ）比较小。则设计加速度反应谱Sa（ωj，ξ）和对应的功率谱G（ωj）之间的换算关系为：

根据上式，经傅里叶变化，可得到如图2所示的优化前地震波时程曲线。由于Vanmarcke方法提供的是反应谱和功率谱的近似关系，因此，图2中优化前地震波对应的拟合反应谱（图1）和设计反应谱之间存在较大误差。

图2 优化前的加速度时程曲线图

为了进一步提高人工合成地震波对应的反应谱和设计反应谱之间的拟合程度，再用小波函数方法[15]对优化前的地震波进行调整优化。优化后的地震波如图3所示，其对应的反应谱和设计反应谱的拟合程度较高，两者的最大误差仅为9%，达到精度要求，可作为地震动施加到有限元模型中，进行非线性动力响应分析。

图3 优化后的加速度时程曲线图

2 三维有限元模型建立

现以某悬索桥为研究对象，悬索桥跨径布置为751+1560+600（m），主梁为箱型梁体，中跨设置吊杆，塔高250m。采用有限元分析软件SAP2000建立三维有限元模型（见图4）。塔与梁采用框架单元模拟，主缆采用索单元模拟。现采用一致地震激励模式，故墩和塔底部六个自由度方向全部约束。

图4 悬索桥有限元模型

3 结果分析

桥塔塔底的剪力大小是衡量桥梁抗震性能的重要参数。图5和图6显示了1号塔桥塔底和2号桥塔塔底在人工合成地震波作用下的剪力响应。由于采用了一致激励输入法，两者的响应曲线形状相似。同时，1号塔塔底的剪力绝对值最大为1.3×107N，2号桥塔的塔底剪力响应绝对值最大为1.2×107N，比1号塔最大值减小约7.7%，两者的最大响应均出现在地震开始后的3.4s。出现这种现象的原因可能与邻近桥墩的数量有关：1号塔左跨的桥墩数量共12个，2号塔的右跨桥墩数量为9个，桥墩数量的增加在减小桥梁变形的同时，也增加了桥梁的剪力响应。

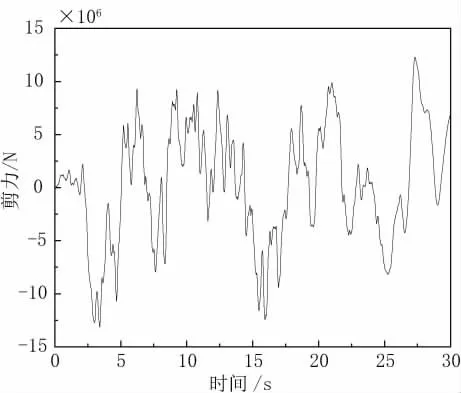
图5 1号桥塔塔底剪力图

1号塔和2号塔塔底的弯矩响应如图7和图8所示，前者的最大值比后者约大5%，相差的幅度小于桥塔塔底剪力的数据。在一致激励的地震作用下，1号塔塔底的弯矩响应特征与2号塔的塔底弯矩响应特征相似，但总体上，前者的响应大小略大于后者。造成这一现象的原因同上一节类似，桥墩数量的增加导致了桥梁变形的减小，同时也造成了弯矩响应的增加。

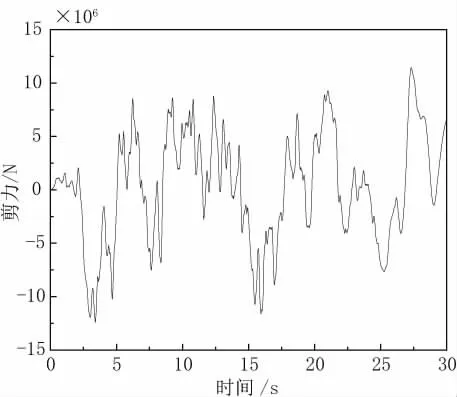
图6 2号桥塔塔底剪力图

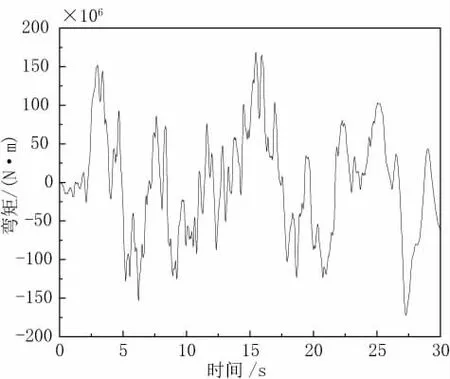
图7 1号桥塔塔底弯矩图

图8 2号桥塔塔底弯矩图

图9 和图10展示了悬索桥1号塔和2号塔塔顶的顺桥向位移，总体上看，两者的位移非常接近，但1号塔在极值处的数值略小于2号塔（相差约0.44%）。出现这个现象的原因，同前面1号塔和2号塔塔底内力响应存在大小差异的原因相同。由于左右跨的长度不同，且桥墩的数量也不同，这就造成了地震波能量传递到桥塔时的变形响应不同。1号塔处的位移响应偏小，而内力响应偏大。

4 结 论

图9 1号桥塔顶部顺桥向位移图

图10 2号桥塔顶部顺桥向位移图

本文采用设计反应谱生成人工地震波，并用小波函数方法对地震波进行优化，得到更接近于设计反应谱的优化地震波。再以某自锚式悬索桥为研究对象，分析该悬索桥在优化地震波作用下的地震响应。得到的结论如下：

（1）桥塔塔底的剪力响应大小和相邻跨的桥墩数量相关，桥墩数越多，桥塔的剪力越大（增大约7.7%）。

（2）两座桥塔塔底的弯矩响应特征相似，但1号塔的弯矩最大值比2号塔的弯矩最大值大5%。

（3）不同桥塔顶部位移响应规律相似，但极值处的大小和相邻跨的桥墩数相关。相邻桥墩数量多的1号塔位移最大值比2号塔的位移最大值小0.44%。