滨海特大高架桥梁抗震优化设计

王文彪

[上海市政工程设计研究总院（集团）有限公司，上海市200092]

0 引言

滨海高架桥梁由于其特殊的地理位置，一般地震烈度较高，桥梁抗震设计存在着一定的特殊性。滨海桥梁服役期长达百年，除地震外还要面对强风、车辆和海洋腐蚀环境等恶劣荷载工况，其运营及耐久性能要求较高，总结及探讨滨海桥梁特点的抗震设计方法具有较高研究意义[1-3]。而且滨海桥梁的墩柱较高，桩基较长，其下部结构方案合理性对桥梁地震动反应影响较大，且对桥梁经济合理性有较大影响[4，5]。本文以工程实例为研究对象，通过建立三维动力模型，分析不同墩柱尺寸和桩基方案对桥梁地震反应的影响，并对桥梁进行延性抗震设计验算，对比分析出经济合理的墩柱尺寸和桥梁桩基数量。对比研究对滨海特大高架桥梁抗震优化设计，对此类型桥梁的下部结构方案合理优化设计，具有重要的工程指导意义[6，7]。

1 工程概况

某市滨海大道高架桥，桥梁全长1536m，全桥跨径布置为7联3×40m+5联36m+3×32m+2×30m连续箱梁，桥墩高约5~10m。全桥均采用钻孔灌注桩基础，均嵌入岩层中，桩基直径1.5m，桩长约70~90m。桥梁整体方案见图1。

桥墩与桩基配筋见图2。

图1 桥梁下部结构方案（单位：mm）

2 地震动参数与分析模型

本文建立桥梁抗震设计的三维空间动力计算模型，分析结构动力特性。采用线性反应谱法以进行地震反应分析，研究结构在E1地震作用（50a超越概率10%）和E2地震作用（50a超越概率2%）两种设防水准地震输入下的地震响应。

图2 桥墩与桩基配筋图（单位：mm）

本场地地震动峰值加速度为0.10g，场地地震分组为第一组，场地类别为Ⅳ类，场地地震动峰值加速度调整系数Fa=1.20，场地特征周期值为0.65s，场地土属软弱地基土，属于建筑抗震不利地段[8-10]。地震动输入分别采取顺桥向与横桥向两种方式。主梁和桥墩均采用梁单元模拟，承台近似按刚体模拟，其质量堆聚在承台质心；二期恒载以均布质量形式加在主梁单元上。桥梁支座布置见图3。据此设定三维模型的支承连接条件，见表1。

图3 支座布置图

桩基础是在承台底加六个方向的弹簧来模拟桩基础的作用，并由承台底部内力按静力方法（m法）反推单桩最不利受力。如4根桩基时，六弹簧刚度见表2。

本文分别以关键典型的中间联3×40m三联和边联3×40m三联为例，在此基础上进行地震反应分析和抗震设计，模型见图4。

3 抗震结构设计

桥墩和桩基础截面的抗弯能力（强度）采用截面积分的方法进行弯矩－曲率（考虑相应轴力）分析，截面混凝土根据需求划分，而单根钢筋单独作为一个网格，见图5。

表1 全桥每联支承连接条件

图4 三联空间动力计算模型

图5 桥墩与桩基础截面计算网格划分

下部结构方案对桥梁地震动反应影响较大，且对桥梁总体方案的经济合理性存在较大影响[11-12]。本工程经计算分析，E1地震作用下，地震分析满足设计要求，本文仅阐述E2地震作用下，对不同墩柱尺寸和桩基数量下，地震动反应和抗震分析设计。

3.1 墩柱尺寸变化

墩柱底部尺寸2.5m×2.0m、2.0m×2.0m和2.0m×1.6m三种情况下，对关键截面墩柱底的地震反应进行分析。静力作用下，该三种截面均能满足规范要求。

墩柱高度较高的中间联的地震反应见表3。表中P2为固定墩，PI表示非固定墩中地震反应最大的墩。

墩柱高度较矮的边联的地震反应见表4。

根据计算结果可知，墩柱尺寸越大，中间联和边联的地震墩底地震反应越大；且纵向地震反应远大于横向。因为随着墩柱尺寸变大，桥梁刚度增大，其地震反应随之增大。因此，在满足静力荷载作用的情况下，墩柱尺寸宜尽量小，本文选择2.0m×1.6m。且经验算，各墩柱尺寸在E2地震作用下，验算均不能满足要求。

表2 各群桩基础的六弹簧刚度

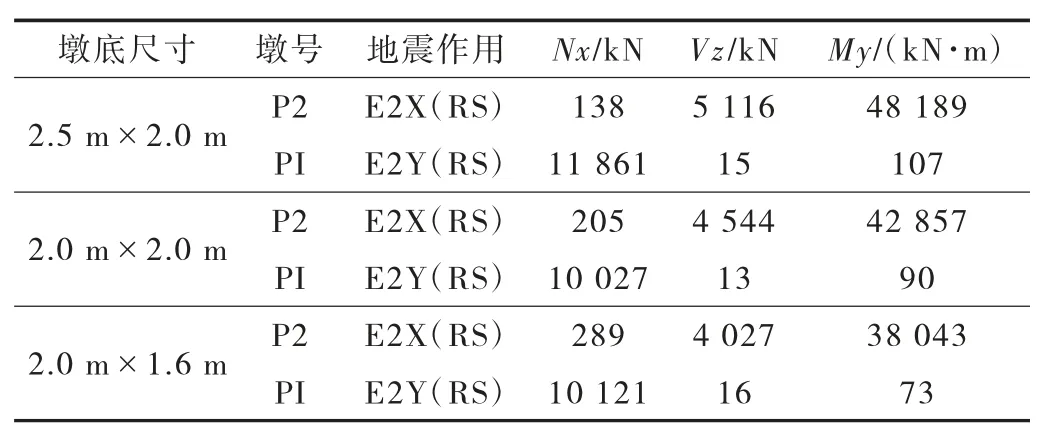
表3 中间联不同墩柱尺寸地震反应

表4 边联不同墩柱尺寸地震反应

3.2 桩基数量变化

本文对6根、5根、4根三种桩基数量情况，对关键截面墩柱底和桩基的地震反应进行分析。桩基布置见图6。

图6 不同桩基方案（单位：mm）

选取不同桩基数量下中间联墩柱底的地震反应，见表5。

根据计算结果可知，桩基数量越多，中间联的墩底地震反应越大；且纵向地震反应远大于横向。因为随着桩基数量增加，桩土六弹簧刚度增大，桥梁底部约束增大，其地震反应随之增大。因此，在满足静力荷载作用的情况下，桩基数量宜尽量少，本文选择考虑4根桩。

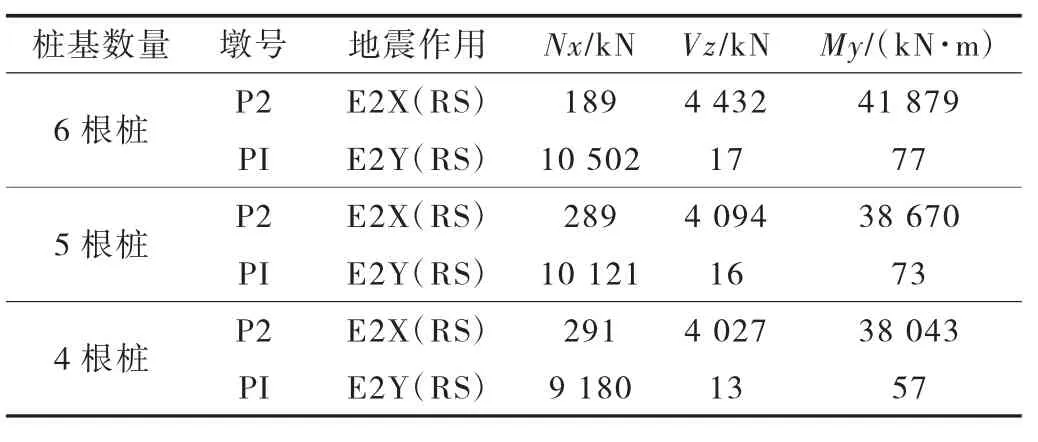
表5 中间联地震反应对比分析

选取不同墩柱尺寸下中间联墩柱底的地震反应，见表6。

表6 中间联地震反应对比分析

经计算分析，E2地震作用下，墩柱尺寸选择2.0m×1.6m，桩基数量为4根时，桩基抗震能力能满足规范要求。

4 延性抗震设计

由上述计算分析可知，在E2地震作用下进行反应谱分析，横桥向地震作用下，各关键截面均能满足抗震性能目标；纵向地震作用下，固定墩P2墩墩底将进入屈服，应进行延性构件变形能力验算；根据计算得到的基础弯矩、剪力和轴力设计值，桩基础的验算采用该设计值和永久作用效应组合后进行。

在延性设计中，动力计算模型除延性构件外，均和前述模型相同。对于延性构件，在E2地震作用下，构件的抗弯刚度采用有效截面抗弯刚度，按式（1）确定：

式中：EC为桥墩的弹性模量（kN/m2）)；Ieff为桥墩有效截面抗弯惯性矩（m4）；My为屈服弯矩（kN·m）；φy为等效屈服曲率（1/m）。

4.1 墩顶位移验算

若墩柱屈服，需按延性构件采用折减刚度（有效截面刚度）计算墩柱的地震反应。以中间联P2号墩柱为例，纵桥向的有效截面刚度为：

在进行桥墩位移验算时，按弹性方法计算出的地震位移应乘以地震位移调整系数c。墩顶的顺桥向水平位移Δd：

在E2地震作用下，一般情况应验算潜在塑性铰区域沿顺桥向和横桥向的塑性转动能力，但对于常规桥梁可验算桥墩墩顶的位移：

表7 列出了各纵向固定墩的位移能力需求比，在E2水准下墩柱的延性能力是足够的。

表7 E2地震作用下墩顶位移验算

4.2 能力保护构件验算

E2地震作用下，若墩柱屈服，按延性构件设计，则为了保证预期出现弯曲塑性铰的墩柱构件不发生脆性的如剪切破坏等破坏模式，并保证不宜用于耗能的构件（能力保护构件）处于弹性反应范围，在确定他们的弯矩、剪力设计值时，应根据墩柱可能出现塑性铰处按实配钢筋，并采用材料强度标准值和轴压力计算出的弯矩承载能力同时考虑抗弯超强的影响来计算得到。

对于桥墩的脆性剪切破坏，必须通过提供较高级别的强度避免。墩柱的抗剪强度按照规范公式计算[13，14]，验算结果见表8。

表8 墩柱底截面抗剪强度验算

桩基作为能力保护构件，计算群桩基础的抗力需求时，应按桥墩塑性铰区截面的超强弯矩计算其设计地震荷载效应，验算结果见表9。

表9 P2墩最不利单桩内力最大值

经验算可知，E2地震作用下，采用延性地震设计理论，该桥梁的位移能力、能力保护构件能力均能满足规范要求。

5 结语

由上述计算分析可知，得到以下结论。

（1）桥梁地震反应随着墩柱尺寸变大而增大，随着桩基数量增大而增大。因此，在满足静力荷载作用的条件下，宜尽量让墩柱尺寸减小，桩基数量减少，静力作用和动力作用分析存在一个相对合理的平衡点。

（2）本工程在E1地震作用下，墩柱、桩基均保持弹性，满足抗震性能目标；在E2地震作用下，纵向输入时固定墩所有墩柱均已屈服。因此，需要进行延性抗震设计，利用墩底塑性铰的塑性变形减小地震内力。

（3）按照基于能力设计方法的延性抗震理论，对结构在E2地震作用下的抗震性能验算表明：各桥墩的位移能力满足抗震设防要求，且具有足够的抗剪能力，不会发生脆性的剪切破坏，各群桩基础保持在弹性范围内工作，抗震性能满足抗震设防标准。