基于空气质量检测数据差异分析及校准的数学建模教学研究

张春红

(湖南科技职业学院，长沙 410004)

1 问题背景

为完善我国的空气质量监测系统，实时有效监控各地区的空气质量情况，中国工业与应用数学学会发起并倡导运用数学模型为空气质量数据的真实性提供理论依据，并协调国家监测控制站点与化工医药矿业冶金等企业的沟通衔接工作，可提供相关研究需要的实时数据，鼓励各高校数学工作者开展相关应用理论研究。本研究分析并验证了边远地区和特殊企业使用微型空气质量检测仪得到数据的准确性，分析异常数据产生的原因并提供解决方案，合理校准相关数据的异常差异，为企业环保生产提供有效参考依据，为优化社会生活环境提供实力支撑。

2 问题分析

对某地区自建点空气质量检测数据进行预处理，与同一时间国控点数据进行比较，利用R软件对“两尘四气”数据进行描述性统计，分析数据的集中趋势和离散趋势。对预处理数据进行极差法的无量纲处理并利用Matlab软件计算关联度系数，得到“两尘四气”浓度与各气象参数的关联度。为分析国控点数据与自控点气象参数的关系，利用Matlab软件建立BP神经网络模型进行探讨。针对变量间复杂的非线性关系建立BP神经网络模型，选取部分数据进行网络训练得到拟合优度和预测精度较高的模型，利用模型中的预测值对自建点的数据进行校准。

3 模型的建立与求解

3.1 数据统计处理分析

3.1.1 监测点“两尘四气”浓度数据的描述性统计

Step1：数据的预处理。根据自建点检测的数据，利用Python语言对每小时段的数据进行平均化，与国控点数据一一对应。删除存在缺失的数据，最终得到4 200个观测时间点上的数据。

Step2：利用R软件对预处理好的数据进行描述性统计和变量的密度曲线估计。

Step3：结果分析。国控点和自建点观测到不同因素浓度数据在集中趋势和离散趋势的差异。从极差的数据来看，两个监测点的数据基本一致。从密度曲线来看，两个观测点存在明显差异，国控点数据分布较为平、扁，更趋近正态分布，自建点数据偏尖峰分布，两者存在较大差异。

3.1.2 国控点与自建点监测数据差异的动态变化分析

通过对预处理后的数据进行描述性统计分析和密度曲线分析，可初步了解来自两个监测点不同变量在集中趋势和离散趋势上存在差异，利用R软件进一步分析数据，探索国控点和自建点“两尘四气”浓度动态变化趋势及其差异情况。

3.2 差异影响因素分析

对预处理后的数据进行探索性分析可知，国控点和自建点“两尘四气”浓度数据存在一定差异，利用关联度分析法分析天气参数(风速、降雨量、压强、温度、湿度)与“两尘四气”浓度影响因素之间的强弱主次关系。

3.2.1 灰色关联度分析方法模型的建立

选取自建点监测数据中六项影响因素的浓度及五类气象参数作为研究对象，找出气象参数与浓度影响因素之间的关系，建立灰色关联度分析法模型：

(1)定义空气影响因素每小时平均浓度数列为参考数列，气象参数数列为比较数列，则参考数列为x0(k)，比较数列为xi(k)。

(2)因气象参数数列中各变量量纲不一样，为不影响分析结果，进行无量纲化。在进行灰色关联度分析之前对各指标因素进行量化，转化为定量因素，便于建立预测模型。

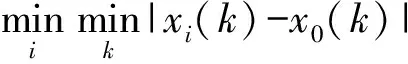
3.2.2 灰色关联度分析方法模型的求解

Step1：在预处理数据中，使用极差法对自建点包含的“两尘四气”和气象参数数据进行无量纲化处理。

Step2：令模型中的分辨率参数ρ=0.5，使用Matlab软件得到空气影响因素及PM10与各个气象要素的关联系数。

Step3：通过关联系数最终得到“两尘四气”与气象参数关联度，关联度分析得出：风速与CO、NO2、SO2浓度有一定的相关性，影响较大，风速过高会使CO、NO2、SO2浓度升高，造成监测数据的误差。PM10、SO2、NO2浓度与温度有一定的相关性，温度升高，则对应变量增加。CO、NO2和SO2浓度与天气参数的关系最为密切，表明天气因素干扰会对观测数据造成较大误差。

3.3 数据的校准

3.3.1 建立BP神经网络模型

“两尘四气”浓度与气象参数间复杂的非线性关系，可以运用BP神经网络模型来拟合，利用国控点数据对自建点“两尘四气”浓度数据进行校准。BP神经网络过程图如图1所示。

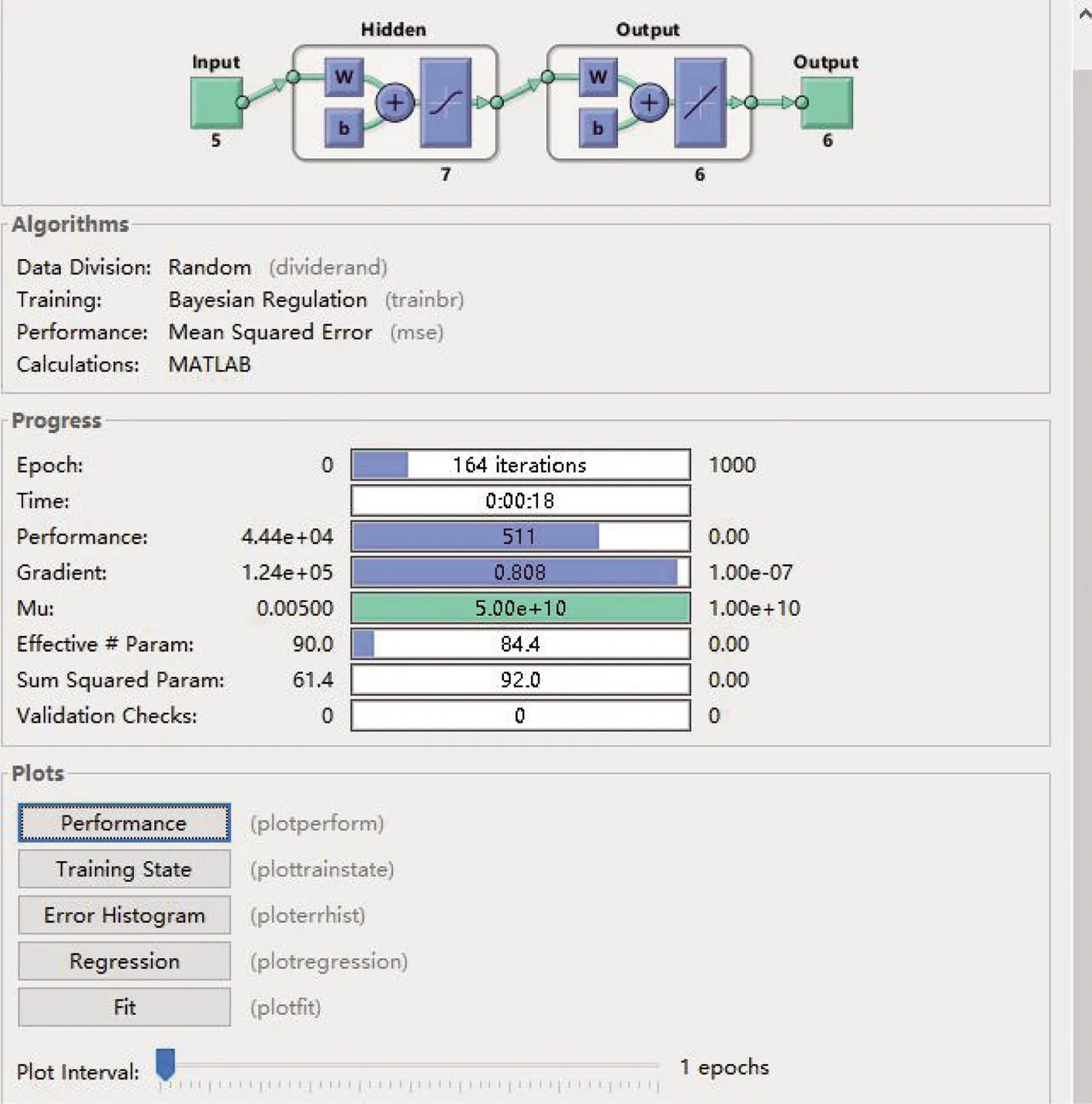
图1 BP神经网络过程图

根据BP神经网络原理，对于输出层，有：hk=f(netk),k=1,2,…,6

对于隐层，有：yj=f(netj),j=1,2,…,m

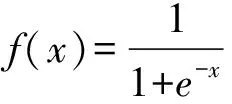
神经网络算法步骤：

Step1:初始化。对权值矩阵W和V赋随机数，将样本模式计数器p和训练次数计数器q置为1，误差E置0，学习率η设为0～1内的小数，网络训练后达到的精度Emin设为一个正的小数。

Step2：输入训练样本，计算各层输出。用当前样本对向量数组X和D赋值，并计算Y和H各分量。

Step3：计算网络输出误差。共有12对训练样本，网络对于第i个样本具有误差。

Step4：计算各层误差信号。

Step5：调整各层权值。权值调整量为：

Step6：检查是否对所有样本完成一次轮训。若p<4，计数器p、q加1，返回Step2，否则进行下一步。

Step7：检查网络总误差是否达到精度要求。若ERME

3.3.2 结果分析和对自建点数据的校对

使用Matlab软件分析自建点气象参数和国控点“两尘四气”浓度的预处理数据。神经网络模拟的指标与监测值误差很小，训练后得到“两尘四气”浓度的预测值。部分预测点数据如表1所示。

表1 “两尘四气”浓度部分预测值

以上关于PM2.5等五个特征因子的模拟实验，说明模型预测的值误差偏小，波动较为稳定，达到了理想的预测效果，可以利用国控点的预测值对自建点数据进行校准。

重复模拟次数，发现特征因子中温度和湿度的影响因子最大。实验结果显示，所采用的模型预测空气污染指数准确性较高。外在因素中温度和湿度可以看做是影响空气质量最主要的两个因素，因此，在平时空气污染较严重的情况下，可以向空中洒水，加大空气中的湿度来降低空气污染。

4 结论

本研究以数据分析为前提，结合数学模型对空气质量检测数据进行了差异分析并校准，有效利用了数学建模教学中数据处理的方法和分析原理，是以现实数据为依据演示数学建模教学过程的典型范例。