求解奇异线性系统的右预处理MINRES 方法

洪琳依

(温州大学数理学院，浙江温州 325035)

本文讨论如下大型稀疏线性方程组的求解：

A∈Rn×n，x,b∈Rn，r= rank(A)＜n，其中A是对称的，且b∈R(A)，我们称之为相容线性系统.

下面介绍一下本文使用的符号.R(.)表示对应矩阵的值域，N(.)表示矩阵的零空间，rank(.)表示矩阵的秩，AT表示A的转置，Im为m阶的单位矩阵，R(A)⊥表示R(A) 的正交补，⊕表示直和，A+为满足如下条件的Moore-Penrose 广义逆[1]：

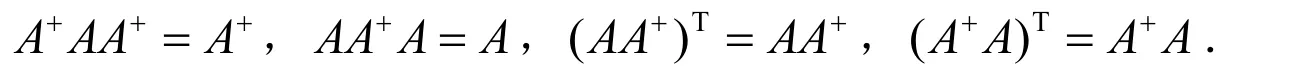
MINRES（Minimal Residual）是求解大型对称线性系统的流行方法之一.最近，Sugihara 等人[2]采用右预处理MINRES 方法对奇异线性系统Ax=b进行了求解，其预处理子是非奇异的.众知，构造预处理子的一个基本原则是让预处理子能够逼近线性系统的系数矩阵，而奇异线性系统的系数矩阵是奇异的，所以选取奇异矩阵作为奇异线性系统的预处理子是合理的想法.本文主要关注奇异右预处理子的构造并用其加速MINRES 算法.下面首先给出MINRES 的简单介绍.

给定初始的x(0)∈Rn，记初始的残差r(0)=b−Ax(0)，则MINRES 按如下方式搜索近似解x(k)：

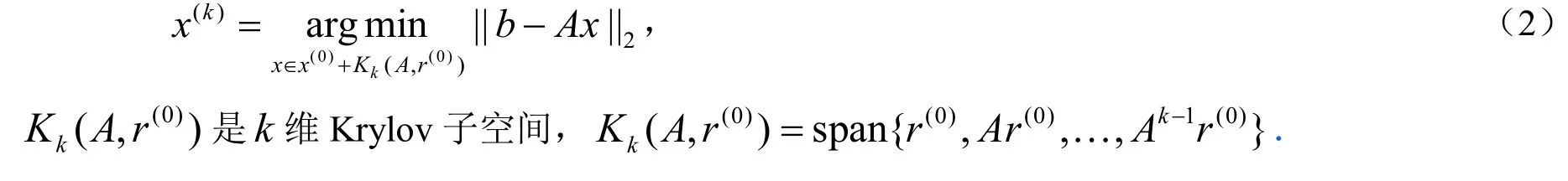
1 右预处理的MINRES 算法

引理1[3]A的分裂：A=M−N，若R(A)=R(M)，N(A)=N(M)，则称分裂A=M−N为恰当分裂.

接下来将要讨论的预处理子M皆满足上述的恰当分裂，且M为对称正半定（SPSD）矩阵.对（1）经过M右预处理后，系统可以转化为求解以下方程组：

直接用MINRES 方法来求解（3）是不可行的，因为AM+不是对称矩阵.因此考虑构造一个新的半范数.

因为所讨论的A和M都是对称的，所以有：

因此AM+在(,)M+下是自伴的，可以通过找到

来求解（3）.下面给出奇异右预处理MINRES 算法.

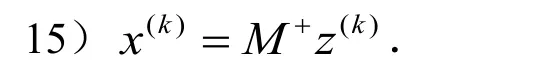
2 右预处理的MINRES 的收敛分析

引理2[4]若R(A)=R(M+)，则有：1）R((M+A)T) =R(AT)；2）R(M+A)=R(MT).

引理3[5]若A∈Rn×n，且是非奇异的，则用GMRES（Generalized Minimal Residual）算法求解Ax=b时，迭代至多在第n步收敛.

定理2 对于线性系统Ax=b，A∈Rn×n且对称，m是矩阵A的秩，m＜n.若A=M−N是恰当分裂，M是SPSD 矩阵，当利用奇异右预处理MINRES 方法求解时，对于 ∀b∈R(A)，∀x(0)∈R(A)，迭代至多在第m步收敛.

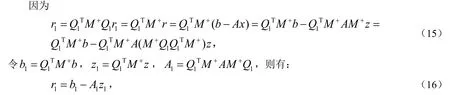
易得A1是对称的.由引理2 可得：

由文献[5]可知，GMRES 与MINRES 的不同是，GMRES 是基于Arnoldi 过程，而MINRES是基于Lanczos 过程.而Lanczos 过程可以看成是当矩阵是对称时Arnoldi 过程的一种简化.所以对于对称的矩阵，GMRES和MINRES可以看成是等价的.所以根据引理3可以得到，利用MINRES求解，迭代至多在第m步收敛.

故对于 ∀b∈R(A),∀x(0)∈R(A)，利用奇异右预处理求解奇异线性系统时，迭代至多在第m步收敛.证毕.

下面给出算法2.

3 数值实验

根据上面的理论分析，通过一些数值实验来证明用奇异右预处理MINRES 迭代法求解奇异线性系统的有效性和可行性.考虑如下奇异鞍点问题：

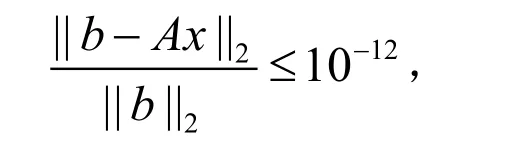
“+”表示CPU＞10 000.

第一种，预处理子为I时，即不做预处理，记为PI.

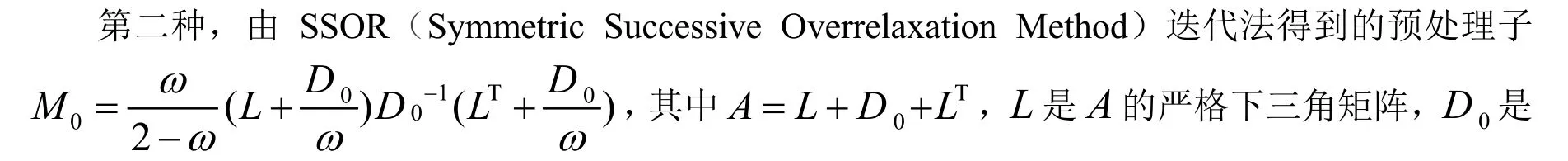
第三种，预处理子是根据HSS（Hermite/ 反Hermite 分裂）[7]迭代法得到的预处理子，并取最优参数，记为PHSS.

当n=64 时，应用4 种不同的预处理子，根据奇异右预处理MINRES 迭代算法求解算例1和算例2 得到的比较图见图1 和图2.表1、表2 给出了不同预处理子下的右预处理MINRES 数值实验得到的IT、CPU、RES 值.

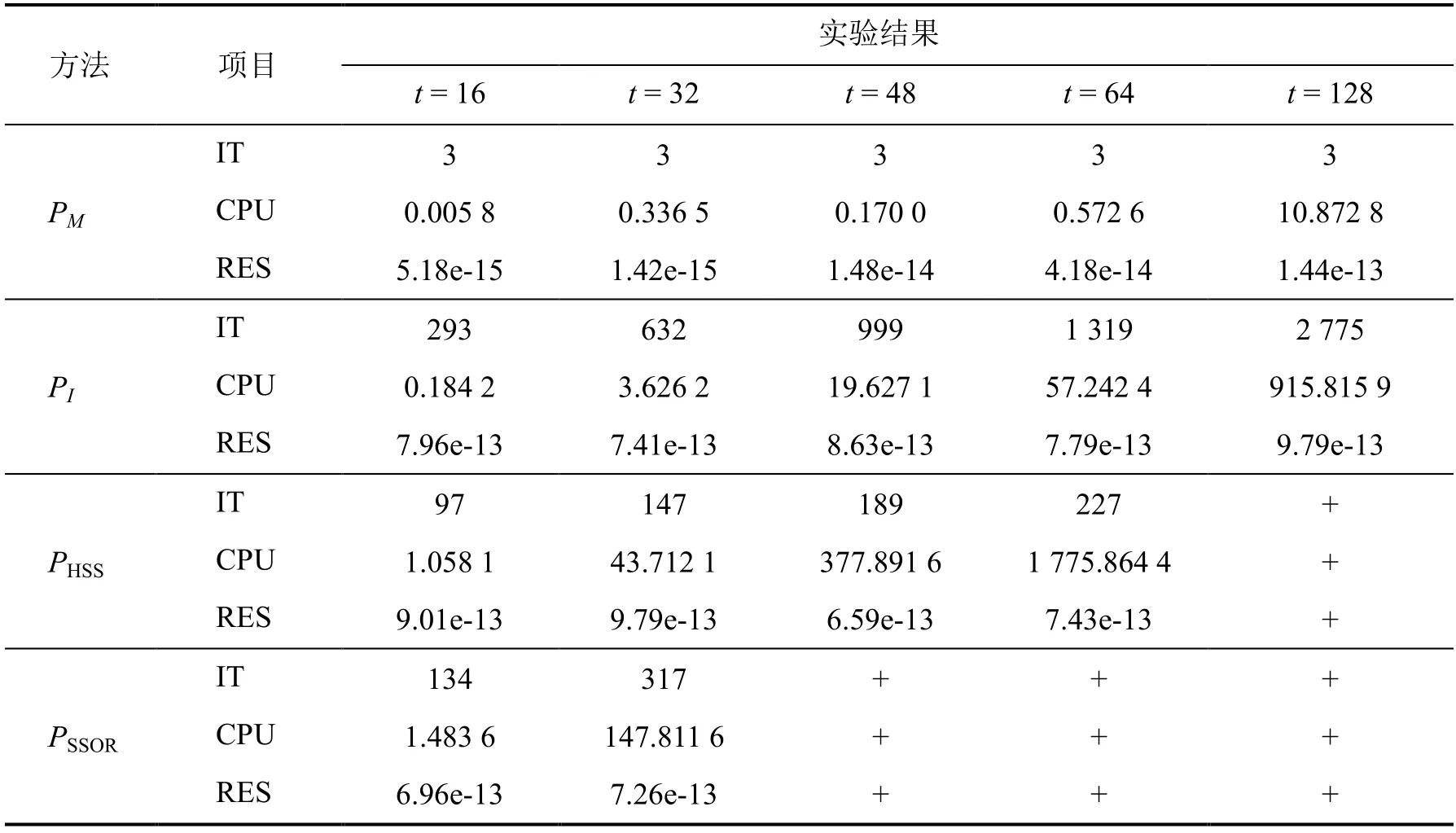
表2 4 种不同预处理子下的右预处理MINRES 方法对算例2 的实验结果

图1 4 种不同预处理子下求解算例1 的结果（n=64）

图2 4 种不同预处理子下求解算例2 的结果（n=64）

表1 4 种不同预处理子下的右预处理MINRES 方法对算例1 的实验结果

由图1、图2 可以明显看出，用预处理子为M的奇异右预处理MINRES 方法求解算例1 和算例2 时的收敛速度比用其他3 种预处理子的快.由表1、表2 也可得出同样的结论.所以，无论从哪个角度比较，求解算例1 和算例2，采用以M为预处理子的奇异右预处理MINRES 方法都比采用其他3 种预处理子的更为有效.