链式STATCOM载波移相调制开关频率的优化方法
(南昌工程学院 1.南昌市高压大功率电力电子技术重点实验室;2.机械工程学院,江西 南昌 330099)
链式STATCOM是一种基于大功率换流技术的静止无功补偿装置。它采用了多个单相逆变桥级联的结构形式[1],可以通过吸收或发出连续调节的无功功率来稳定连接点处的电压,提高系统的负荷能力。除此之外,链式STATCOM还有着原理简单、控制方便、易于模块化、容易实现冗余容错等诸多明显优点,在工业中的应用十分广泛[2-3]。
调制技术是链式STATCOM研究的关键技术之一,而开关频率是影响调制效果的关键因素,选择合适的开关频率有利于达到最好的调制效果,使系统的各项指标满足工业要求。对于链式STATCOM系统,目前最为常用的调制手段是单极性倍频载波移相调制策略,张祥虎[4]等从原理层面分析了载波移相调制方式,通过与其他调制方法的对比,验证了这种调制方法的优越性。Zhang[5]等提出了一种基于VF的PWM算法。Xu[6]等根据载波移相调制策略的等效开关频率高、开关损耗小的优点提出了多电平控制策略。She[7]讨论了载波移相调制对链式STATCOM系统的影响。然而,现有文献并没有给出开关频率与调制效果之间定量的分析过程,无法为开关频率的最优设计提供指导。
因此,在现有研究基础上提出了一种基于载波移相调制的链式STATCOM的开关频率的优化方法。通过建立开关频率与链式STATCOM的相关参数之间的数学模型,分析开关频率对调制效果的影响,得出最合适的开关频率。
1 链式STATCOM的电路结构
链式STATCOM装置的结构有两种接线形式,分别是三角形结构和星形结构,其中三角形结构没有中性点,而星形结构有中性点。以星形链式STATCOM为例,其电路原理图如图1所示。
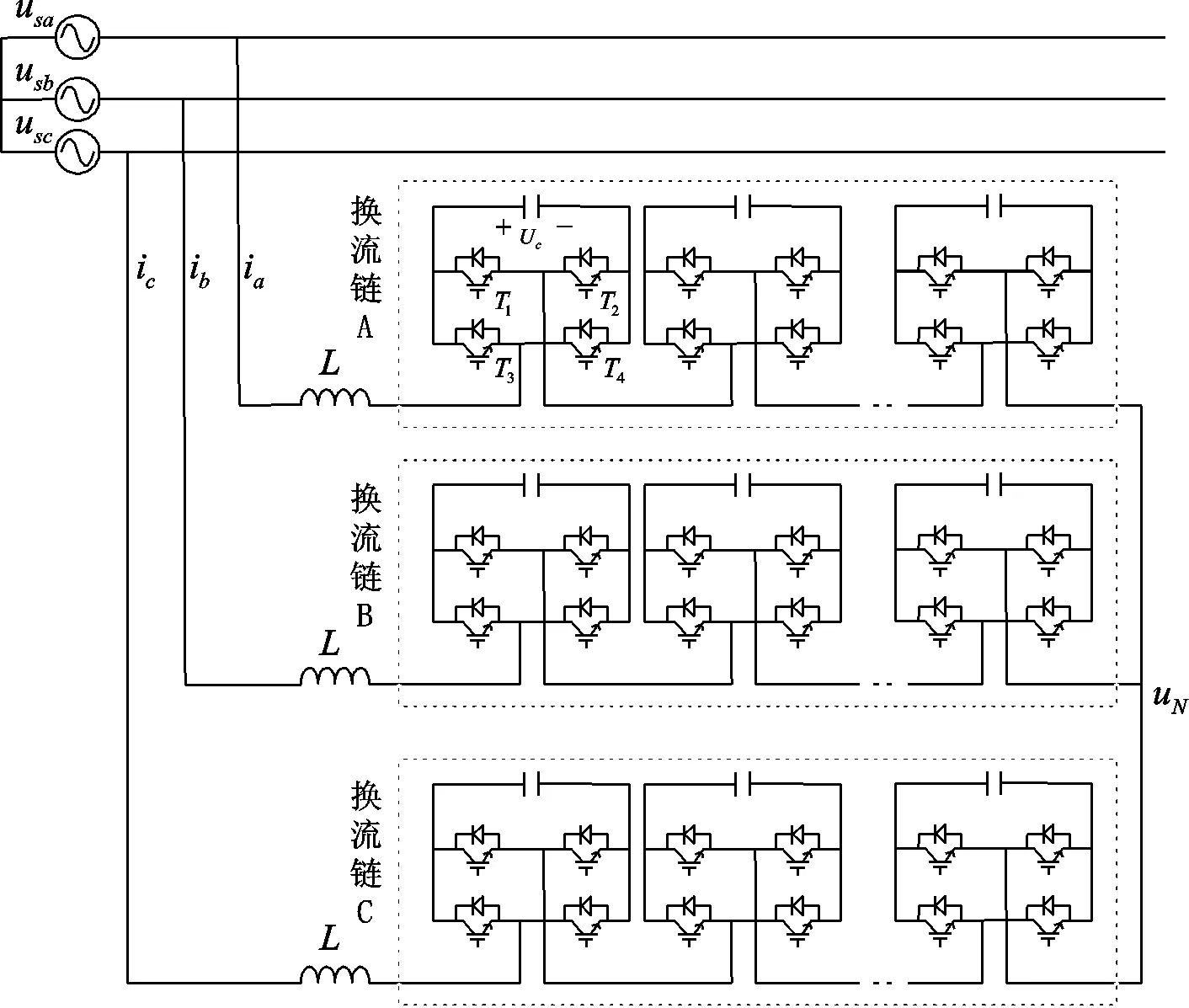
图1 星形链式STATCOM电路原理图
由图1可知,链式STATCOM每一相都由N个功率单元(电压源逆变器)级联而成,这些功率单元组成一个换流链,然后通过连接电抗器接入系统。
链式STATCOM的优点之一是可以实现模块化设计,这是由于无论是星形结构还是三角形结构,其所用的功率单元的结构完全相同。在实际应用中,将这些完全相同的功率单元串联起来,可以提高设备的电压等级,功率模块结构为电压源逆变H桥,其可以产生3电平输出:当同时导通T1和T4时,该模块可输出一个为Uc的正电平;当同时导通T2和T3时,可输出一个-Uc的负电平;当同时导通T1和T2或T3和T4时,则输出零电平。
将N个功率单元串联形成换流链时,N个H桥单元输出电压经过叠加可得到2N+1级的阶梯电压波形[8-9],实现多电平输出。
2 开关频率与链式STATCOM性能的关系
2.1 开关频率与模块数之间的关系
为了讨论开关频率与模块数之间的关系,首先讨论在一个控制周期内系统的变化。由于三相系统的对称性,只需要讨论一相便可以推广到其他相,以图1所示的星形链式STATCOM为例,对于三相对称系统来说,uN=0,以下讨论以此为前提。以图1中的换流链A为例,设m为调制比,N为单相模块数,ω为调制波角频率,其调制波可定义为
(1)
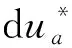
(2)
式中f为电网基波频率,fctrl为控制器控制频率。
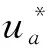
(3)
则有
2mNπ(f/fctrl)sin(2πf/fctrl)=1.
(4)
在实际工程中,一般有fctrl≫2πf,则有
sin(2πf/fctrl)≈2πf/fctrl.
(5)
将其代入式(4)中可得
4mNπ2f2/fctrl=1.
(6)
因此有
(7)
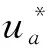
(8)
由此可以求得临界控制频率f2为
f2=2πfmN
(9)
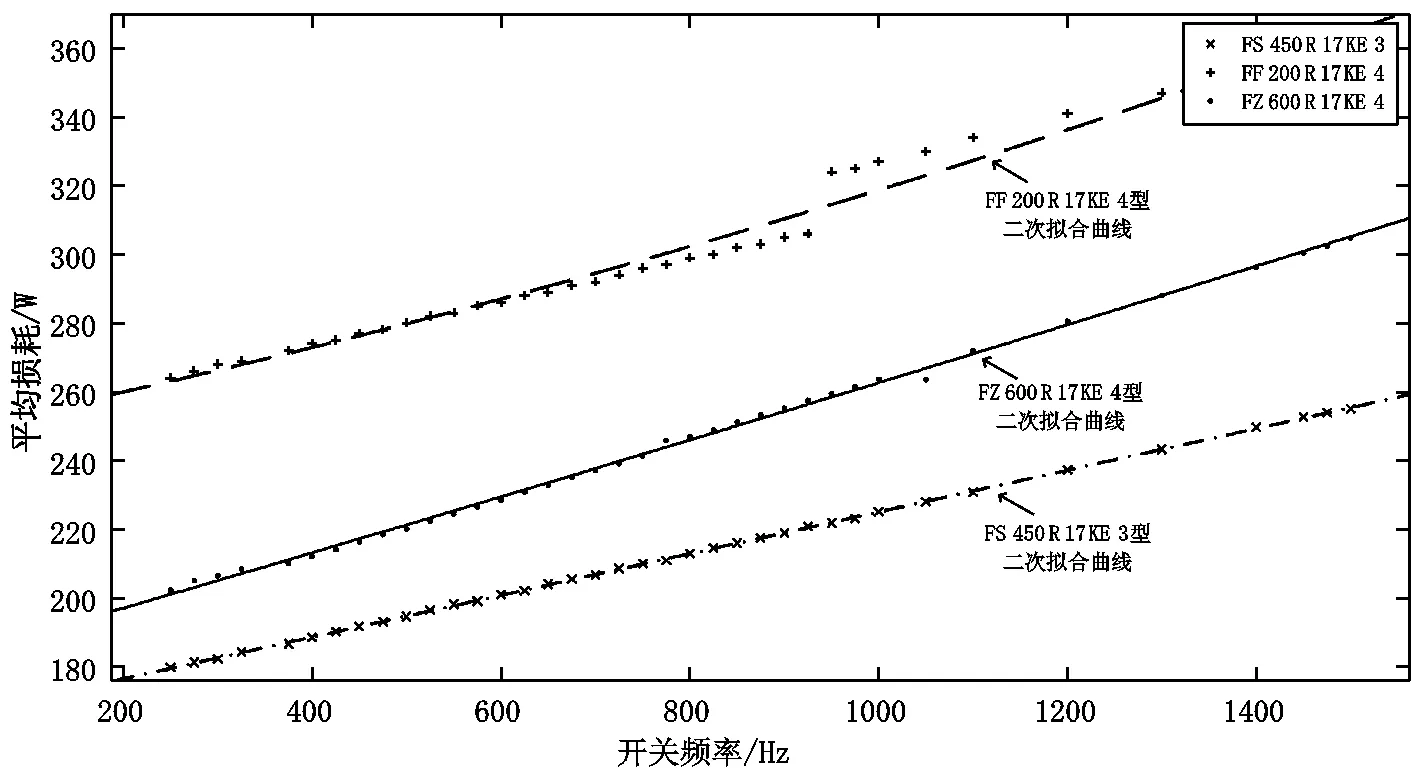
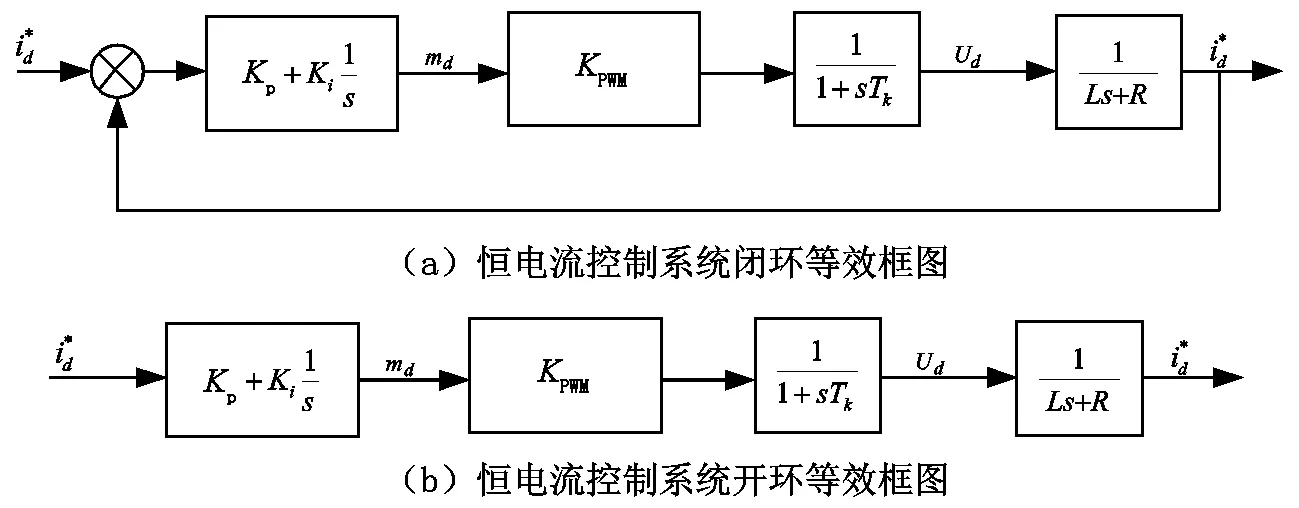
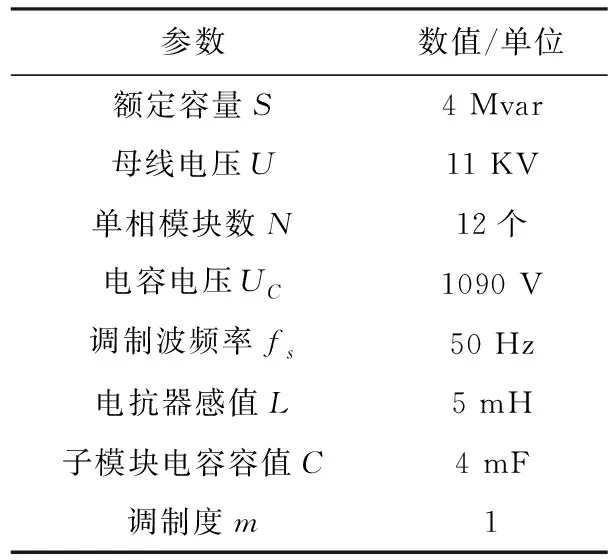
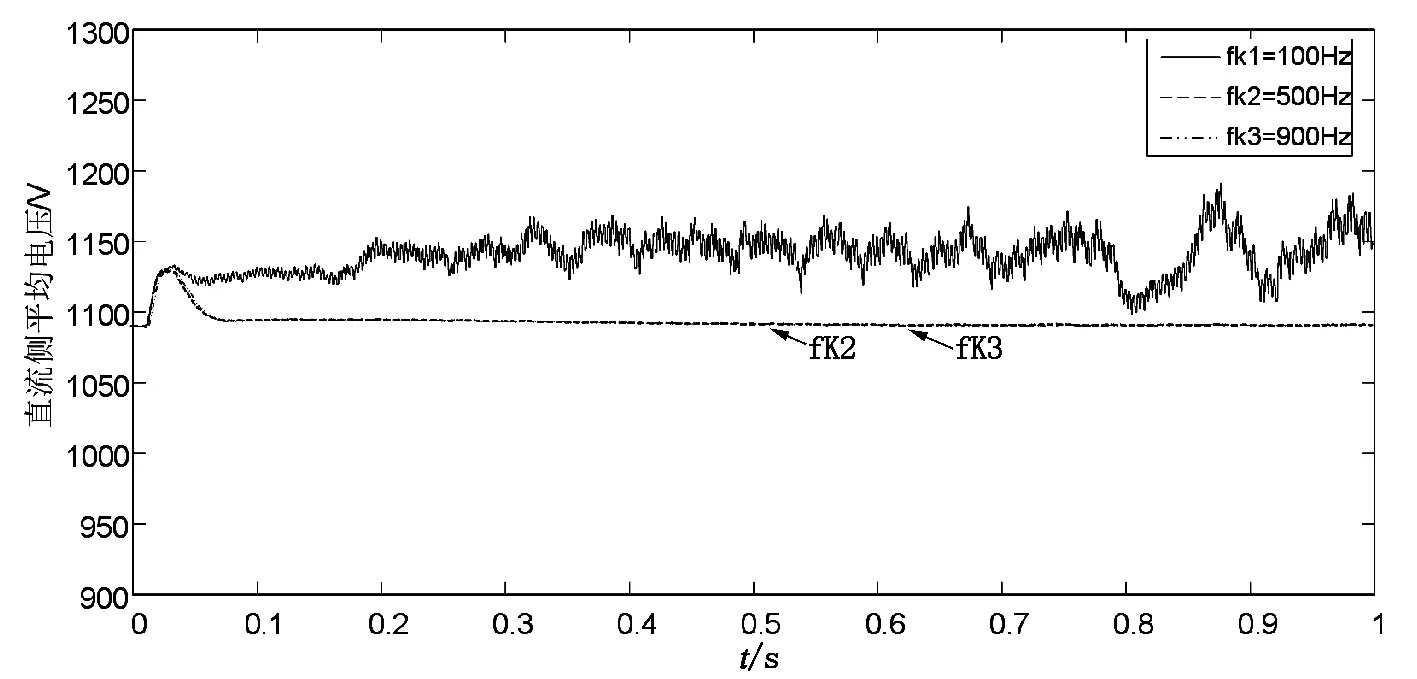
在实际应用中,控制频率通常满足f1 (10) 设备的开关损耗是开关管开通与关断过程中产生的损耗。链式STATCOM的开关管为IGBT,其开关损耗包括IGBT及其反并联二极管的损耗。 以FS450R17KE3、FF200R17KE4、FZ600R17KE4型IGBT为例,通过开关损耗监控软件,可以测得在不同开关频率下的开关管平均损耗,将其绘制成开关管的平均损耗与开关频率的曲线,如图2所示。 图2 开关频率与IGBT平均损耗关系曲线 由图2可知,开关频率与开关管平均损耗正相关。本文将以损耗与性能相对平衡的FZ600R17KE4型IGBT为例进行下一步研究,通过二次拟合可得其损耗曲线函数为 (11) 在实际系统中,往往存在延时,一般情况下系统的延时近似于一个开关周期。换流链采用了基于DQ解耦的恒电流控制[10],其闭环控制简化框图如图3所示。 图3 链式STATCOM闭环控制框图 在控制系统中,延时环节的传递函数为e-sTk,其中Tk为开关周期,而在实际工程中Tk一般很小,因此延时环节e-sTk≈1/(1+sTk)。根据文献[11]可知恒电流控制系统结构可等效为如图4所示。 图4 恒电流控制系统等效控制框图 可得到相应的开环传递函数为 Gi(s)=KPWMGPI(s)Gdelay(s)Gr(s). (12) 其中 GPI(s)=Kp+Ki/s≈Kp, 则有 (13) 此处定义K=KPWM·Kp/L. 可得其幅相特性 (14) 可以求得截止频率ωc和穿越频率ωx分别为 (15) 则进一步可得幅值裕度和相角裕度 (16) 根据式(16)可知,系统的幅值裕度趋于无穷,相角裕度与系统开环增益和开关周期相关,选择合适的PI参数,可以保证系统稳定,且若保持其它参数不变,当Tk增大时,会导致相位裕度减小,即当开关频率增大时系统的稳定性会变差。 本文以容量为4Mvar,母线电压为11kV的链式STATCOM为例来验证所提开关频率的优化方法。相关参数如表1。 式(10)得出了开关频率与模块数之间的关系,代入相关数据可求得: 218Hz (17) 式(11)得出了开关频率与平均损耗的函数关系式。由于在实际工程中,一般要求开关损耗低于总功率的1%,在4 Mvar的链式STATCOM中开关损耗应低于40 000 W。每相有12个基本功率模块,每个模块中有4个开关管,则一共有144个开关管,因此每个开关管的损耗应低于40000/144=277.8 W,即ploss-av<277.8 W,则根据函数关系式可得 fk<1180.1 Hz, (18) 式(16)得出了链式STATCOM系统的幅值裕度和相角裕度,在电压等级为11 kV的链式STATCOM中,Kpwm=10 200,PI参数一般为Kp=0.0006,Ki=0.006。工业上一般要求Gm≥6 dB,Pm≥30°,代入相关数据可得 fk≥353 Hz. (19) 结合式(17)~(19),可得在容量为4 Mvar,母线电压为11 kV的链式STATCOM系统中开关频率应满足 353 Hz≤fk<754 Hz. (20) 为了验证本文提出的链式STATCOM开关频率优化方案,利用MATLAB/Simulink搭建了一个基于CPS-SPWM调制的链式STATCOM仿真系统。仿真中各参数见表1。 表1 4Mvar链式STATCOM相关参数 仿真条件为:星型链式STATCOM的电网输入电压为10 kV,在0.01 s时投入STATCOM。仿真时间设置为1 s,分别测试开关频率为100 Hz、500 Hz、9 000 Hz的输出情况,直流侧平均电压仿真结果如图5所示。 图5 不同开关频率下的直流侧平均电压 由图5可知,当开关频率过小时,系统将变得不稳定,这验证了前文所分析的内容,当开关频率满足条件时,系统将保持稳定。应该注意的是,开关频率的增大将会导致系统的开关损耗的增加。 换流链电流和A相电容电压仿真结果如图6所示。 图6(a)~(b)分别为开关频率为100Hz情况下的换流链电流和A相各子模块的电容电压,此开关频率为本文所讨论的不稳定的情况,仿真结果验证了这一点;图6(c)和图6(d)分别为开关频率为500Hz情况下的换流链电流和A相各子模块的电容电压,此时换流链电流的谐波畸变率为0.94%,电容电压波动率为6.1%;图6(e)和图6(f)分别为开关频率为900Hz情况下的换流链电流和A相各子模块的电容电压,此时换流链电流的谐波畸变率为1.2%,电容电压波动率为5.7%。可见在各开关频率下,换流链电流都趋于稳定,且谐波畸变率都符合工业要求,但可以看出,在本文所提优化开关频率区间内,其换流链电流的谐波畸变率要比其他两种情况要低;而对于电容电压,随着开关频率的增大,电容电压波动率随之降低,另外,其稳定情况有明显改善,证明了随着开关频率的增大,系统的稳定性也随之增强。 图6 仿真结果 为进一步验证所提开关频率优化方法,搭建母线电压为11kV,容量为4Mvar的链式STATCOM实验平台,实验装置如图7所示。将开关频率设置为本文得出的开关频率区间。为不失一般性,这里将开关频率选择为500Hz,利用示波器采集换流链电流和电容电压,其波形如图8所示。 图7 链式STATCOM实验设备 图8 链式STATCOM的实验波形 图8中波形1为系统稳态时的功率模块交流侧电压稳态时的输出波形,可见实验所得数据为实验设备稳态时的输出,其有效值为701V;波形2为稳态时的直流侧平均电压,其平均值为1 090V;波形3和波形4分别为A相遇B相的输出电流,其有效值为211A,对应的峰值为300A,可见仿真结果与实验结果一致。 本文分析了采用载波移相调制技术的链式STATCOM的开关频率与单相模块数、开关损耗、系统稳定性之间的关系,并以母线电压为11kV,容量为4Mvar的链式STATCOM为例,根据工业需求确定了相应的开关频率的范围,区分这些范围的并集,得到最佳开关频率范围,实现开关频率的优化。 分析表明,随着开关频率的增大,系统稳定性也越好,但是相应的开关损耗和延时都有所增加。本文通过建立链式STATCOM相关参数与开关频率之间的数学模型,可以得到合适的开关频率要求,从而达到兼顾各参数性能的目的。2.2 开关频率与开关损耗之间的关系
2.3 开关频率与稳定性之间的关系

Gr(s)=1/(Ls+R)≈1/Ls,
Gdelay(s)=1/(1+sTk).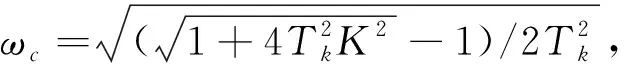

3 计算与验证
3.1 计算
3.2 仿真验证

3.3 实验验证

4 结束语

