基于同心拱模型的桩承式加筋路堤简化分析方法
冯苏阳 徐日庆 俞建霖 程 康 申 硕
(浙江大学滨海和城市岩土工程研究中心, 杭州 310058)(浙江大学浙江省城市地下空间开发工程技术研究中心, 杭州 310058)
近年来,桩承式加筋路堤在公路软土地基处理工程中得到了广泛的应用.与传统的排水固结法、堆载预压法相比,桩承式加筋路堤技术可以显著缩短施工工期,易于控制工后沉降,且适用于复杂的地质条件.文献[1]指出,桩承式加筋路堤荷载传递的主要机制是路堤填土中的土拱效应及加筋体中的拉膜效应.为此,现行设计方法大都分两步进行:①考虑土拱效应,计算作用在加筋体上的荷载;②对加筋体进行受力分析和变形计算.
桩承式路堤土拱效应的分析计算最早来源于Terzaghi[2]提出的活动门试验.此后,Hewlett等[3]提出了半球拱模型,并被英国规范BS 8006-1[4]推荐使用.在此基础上,Zaeske等[5]提出了多拱模型,并被德国规范[6]所采用.后续学者们[7-10]对半球拱模型进行了不同程度的修正和改进.van Eekelen等[11]根据试验观测结果,综合半球拱模型及多拱模型,提出了同心拱模型,文献[12-13]证实其更适合于桩承式加筋路堤土拱效应的计算;然而,该模型计算过程复杂,且仅适用于方形布桩形式,不利于实际工程的推广应用.
对加筋体进行分析计算时常需要预先假设加筋体的变形形状.现有的分析方法大多假设加筋体的变形形状为抛物线[8,10,14-15]或圆弧线[16-18].这些假设均以大量的试验观测为基础,尽管与加筋体实际变形形态存在出入,但可避免复杂的迭代求解,从而简化了计算流程.然而,目前的计算方法大都在二维平面内进行,这与加筋体的三维变形特性不相符.
本文基于同心拱模型,假设加筋体的变形形状分别为旋转抛物面和抛物柱面,提出了一种桩承式加筋路堤的简化分析方法.该方法适用于正方形布桩形式或正三角形布桩形式,可为桩承式加筋路堤的设计提供参考.
1 加筋体变形模型
与二维分析中的抛物线或圆弧线假设不同,基于三维数值模拟结果[19-20],本文将中间区域的加筋体记作第1类加筋体,假设其变形曲面为旋转抛物面;将相邻两桩间条带区域的加筋体记作第2类加筋体,假设其变形曲面为抛物柱面.
为简化分析,本文在推导过程中还进行了如下假设:① 路堤填土是均质且各向同性的,填土高度大于土拱临界高度,填土内可以形成完整土拱;② 加筋体是均质且各向同性的,忽略其自重;③ 加筋体在桩帽边缘处固定,仅发生线弹性变形;④ 桩体刚度足够大,不考虑其自身压缩变形.
1.1 正方形布桩形式
如图1(a)所示,选取虚线所围成的区域为研究单元,加筋体A属于第1类加筋体,加筋体B1~B4均属于第2类加筋体.记桩帽边长为a,桩间距为s,加筋体竖向最大变形为δmax.取加筋体A的中心为坐标原点,建立图1(b)中的笛卡尔直角坐标系,其中x轴垂直于路堤中心线,y轴平行于路堤中心线,z轴竖直向上.

(b) 立面图
对于第1类加筋体,其曲面方程可表示为
(1)

(2)
1.2 正三角形布桩形式


(a) 平面图

(b) 立面图
对于第1类加筋体,其曲面方程可表示为
(3)

(4)
2 同心拱模型下加筋体上方荷载计算
2.1 第1类加筋体
同心拱模型在第1类加筋体上方可视为同心半球土拱[11].设半球的半径为R,取高为dR、球心角为dα的拱顶土微元体进行受力分析(见图3).根据径向平衡条件可得
(5)
式中,σR为径向应力;σα为切向应力;γ为路堤填土的体积质量.

图3 同心半球土拱顶部微元体受力分析图
当路堤填土高度大于临界高度时,同心拱模型认为各位置均处于极限状态,则
(6)

联立式(5)、(6)可解得
(7)
式中,C1为任意常数,需根据布桩形式的不同,结合边界条件确定取值.

(8)
式中,H为路堤填土的高度.将式(8)代入式(6)和(7)可得
(9)
(10)
在极坐标系下,对σα在第1类加筋体所在范围内进行积分,可得到第1类加筋体所承担的竖向荷载为
(11)
式(11)中被积函数的原函数无法用初等函数表示,故采用数值积分的方法计算其近似值为
(12)

(13)
Γ1与φ有关.一般而言,路堤填土的内摩擦角为20°~45°[22].为便于实际工程应用,在满足计算精度的条件下,选用六次多项式来表示Γ1和φ间的关系式为
Γ1=103.521 41-21.083 09φ+1.785 3φ2-
0.079 61φ3+1.9763×10-3φ4-
2.593 23×10-5φ5+1.411 14×10-7φ6
(14)
第1类加筋体经同心半球土拱转移至第2类加筋体的均布荷载为
(15)

(16)
将式(16)代入式(6)和(7),可解得
(17)
(18)
将σα在第1类加筋体所在区域内积分,可得

(19)
采用数值积分的方法对式(19)进行简化可得
(20)


(21)
分别选用四次多项式和五次多项式来分段表示Γ2和φ间的关系式,则

(22)
第1类加筋体经同心半球土拱转移至第2类加筋体的均布荷载为
(23)
以上推导均未考虑路堤顶面受荷情况.当路堤顶面受到均布荷载q时,需对由式(13)或(21)得到的Fsq进行修正,即
(24)
式中,F′sq为路堤顶面作用均布荷载q时第1类加筋体所承担的竖向荷载.
2.2 第2类加筋体
同心拱模型在第2类加筋体上方可视为同心半圆土拱[11].设半圆的半径为r,取高为dr、圆心角为dθ的拱顶土微元体进行受力分析(见图4).

图4 同心半圆土拱顶部微元体受力分析图
根据径向平衡条件可得
(25)
式中,σr为径向应力;σθ为切向应力.
模型各位置均处于极限状态,则
(26)
考虑边界条件
(27)

(28)
第2类加筋体所承担的竖向荷载Fst可由σθ在第2类加筋体所在区域内积分得到.
1) 当桩体为正方形布置时,有
(29)
2) 当桩体为正三角形布置时,有
(30)
当路堤顶面受到均布荷载q时,需对由式(29)或(30)得到的Fst进行修正,即
(31)
式中,F′st为路堤顶面作用均布荷载q时第2类加筋体所承担的竖向荷载.
3 加筋体受力平衡方程
图5为加筋体的受力示意图.图中,T为桩帽边缘处单位宽度上第2类加筋体所承受的拉力;ζ为第2类加筋体在桩帽边缘处的切线与水平面的

图5 加筋体受力示意图
夹角;Fup1和Fup2分别为地基土对第1类和第2类加筋体的支承力.
3.1 正方形布桩形式
对于第1类和第2类加筋体组成的整体,由竖直方向受力平衡关系可得
4aTsinζ=F′sq+F′st-Fup1-Fup2
(32)
以加筋体B1为例分析第2类加筋体,根据几何关系
(33)
(34)
加筋体B1变形后的长度为
(35)
平均应变可表示为
(36)
式中,l0=s-a为加筋体B1变形前的长度.
文献[1]指出,加筋体内的拉力非均匀分布,桩帽边缘处拉力最大.根据第1节的假设,加筋体变形过程中处于线弹性变形阶段,其应力应变关系服从胡克定律,则单位宽度上加筋体B1所承受的平均拉力为

(37)
式中,J为加筋体的拉伸刚度.
单位宽度上加筋体B1所承受的最大拉力为
(38)
式中,k0为比例系数,根据经验,k0一般取2~5.
地基土对加筋体的反力大小取决于所选用的地基模型.由于加筋体竖向位移较小,为简化计算,这里认为地基土服从Winkler地基假设.在Winkler模型中,地基反力系数Ks可以根据地基土变形模量E0与有效深度hact的比值来进行估算,即
(39)
文献[18]指出,有效深度范围可认为是由路堤荷载和堤顶超载产生的竖向附加应力大于等于自重应力20%的区域.
对于第1类加筋体,有
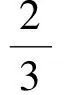
(40)
对于第2类加筋体,有
(41)
将式(24)、(31)、(34)、(38)、(40)、(41)代入式(32),可整理成一个关于δmax的一元三次方程,即
(42)
式中
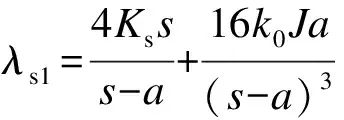
求解式(42)可得到δmax,将δmax代入式(38)可得到T.由此便可求出桩顶平均应力为
(43)
桩间土表面平均应力为
(44)
荷载传递效率为
(45)
3.2 正三角形布桩形式
考虑第1类和第2类加筋体组成的整体,由竖直方向受力平衡可得
3bTsinζ=F′sq+F′st-Fup1-Fup2
(46)
根据几何关系可得
(47)
(48)
(49)
(50)
将式(24)、(31)、(47)~(50)代入式(46),可整理成一个关于δmax的一元三次方程,即
(51)
式中

求解式(51)可得到δmax,将δmax代入式(48)可得到T.由此便可求出桩顶平均应力为
(52)
桩间土表面平均应力为
(53)
荷载传递效率为
(54)
4 案例分析
算例1上海北部郊区某高速公路[23]采用现浇混凝土薄壁管桩联合双向聚丙烯土工格栅加固软土地基,其中管桩正方形布置.利用本文方法对该工程进行理论分析,参数取值如下:H=5.6 m,γ=18.5 kN/m3,c=10 kPa,φ=30°,a=0.893 m,s=3 m,J=1 180 kN/m,k0=3.5,Ks=650 kPa/m.表1列出了路堤填筑完成后的实测值、模拟值、文献[4]结果、文献[6]结果与本文方法所得计算结果对比.为与实测结果相对应,表1中的桩土差异沉降均为两邻桩间桩土差异沉降.

表1 算例1的结果对比
由表1可知,与文献[4,6]的结果相比,本文计算值更接近于实测值.文献[4]在计算时忽略了地基土的反力作用,造成浪费.本文方法基于极限平衡模型和全拱假设,桩顶应力的计算值较实测值略大.相比文献[6],将本文方法应用于工程设计是偏安全的.对于荷载传递效率,本文计算值和实测值之间的误差约为6%,符合工程精度的要求.
算例2申苏皖浙高速公路[24]采用Y形沉管灌注桩联合高强度钢塑土工格栅来处理软土地基,其中灌注桩呈正三角形布置.运用本文方法对该工程进行理论分析,参数取值如下:H=5 m,γ=22 kN/m3,c=0 kPa,φ=35°,s=2.2 m,b=0.770 m,J=1 500 kN/m,k0=3,Ks=600 kPa/m.由于现有规范中没有给出正三角形布桩形式下的计算方法,表2仅列出了路堤填筑完成后本文方法计算值和现场实测值的对比情况.

表2 算例2的结果对比
由表2可知,本文方法计算值与实测值较为接近,其中荷载传递效率的最大计算误差约为6%,从而验证了三角形布桩条件下本文方法的合理性.
5 结论
1) 基于桩承式加筋路堤中加筋体三维变形的特性,将加筋体划分为内部区域和相邻两桩间的条带区域,假设其在空间内的变形形状分别为旋转抛物面和抛物柱面,得到变形曲面方程.
2) 对同心拱模型进行简化,得到正方形布桩和正三角形布桩下加筋体上方荷载的计算表达式.简化后的表达式形式简单,适合应用于工程设计.
3) 根据加筋体在空间的竖向受力平衡方程,分别求解出加筋体的最大竖向变形和最大拉力,从而可得桩顶平均应力、桩间土平均应力和荷载传递效率.
4) 应用本文方法对2个工程实例进行计算,计算值与现场实测值吻合良好,从而验证了该方法的有效性.

