桩承式路堤中土拱效应演变规律宏细观研究

庄 妍，程欣婷，刘永莉，王新岐，杜佃春，曾 伟，李文涛，应春丽

(1.湖北工业大学 土木建筑与环境学院，湖北 武汉 430068；2.东南大学 土木工程学院，江苏 南京 211189；3.河海大学 土木与交通学院，江苏 南京 210098；4.天津市市政工程设计研究院，天津 300392；5.湖北省交通规划设计院股份有限公司，湖北 武汉 430051)

桩承式路堤因其经济高效，同时能够有效提高不良地基承载力、减小地基沉降和不均匀沉降的优点，已在国内外高速公路、铁路、机场及路桥过渡段等工程建设中得到广泛应用[1-3]。在设计过程中，桩承式路堤的沉降计算建立在路堤荷载传递机理的基础上，而土拱效应是桩承式路堤中荷载传递的重要媒介，因此，对于桩承式路堤中土拱效应的产生机理的研究具有重要的工程应用价值与经济意义。Terzaghi[4]最早提出活动门试验以验证土拱效应，土体内部剪切破坏面的发展经历了由曲线形向竖直剪切面的变化过程。近年来诸多学者对土拱效应的理论分析模型展开了研究。Rui等[5-6]采用 PIV 技术采集和分析填料变形特点，揭示了无筋与加筋工况下的二维土拱剪切破坏面的形状。陈其志等[7]采用同样的方法观测到土拱剪切破坏面的形状根据路堤高度与桩净间距的比值不同而发生变化。郑俊杰等[8]通过引入拱顶或桩帽土体单元的状态系数对Hewlett和Randolph[9]提出的土拱效应分析方法进行了改进。Zhao等[10]分析了桩-土模量差对荷载传递大小的影响，建立了考虑桩-土模量差的土拱效应理论分析模型。以上研究主要从宏观角度对土拱效应的发展规律进行分析，而土拱效应产生的内在原因是由于路堤颗粒之间的相互剪切作用使得路堤中的应力发生重分布，因而从微观角度分析土体颗粒体系中应力的传递路径，从而揭示桩承式路堤中的荷载传递规律显得尤为重要。Tran 等[11]对比分析了离散元和有限元两种建模方式下路堤的荷载传递效率以及应力偏转方面的差异。Lai 等[12]基于二维离散元模型从细观角度分析了土拱结构的变化过程。鲍宁等[13]采用离散元软件建立了3种不同高度三维活动门颗粒流模型，分析了路堤内部竖向土压力分布特点、土拱发展模式和土体的沉降变形规律。本文将基于室内模型试验建立桩承式路堤颗粒流模型，从宏观和微观两个角度分析路堤填料自重荷载作用及静载作用下桩承式路堤中土拱效应的形成及演变规律。

1 离散元数值模型建模

基于桩承式路堤平面土拱效应研究的室内模型试验，采用PFC2D软件建立桩承式加筋路堤颗粒流数值模型。将桩承式路堤的离散元颗粒流模型数值模拟结果与室内模型试验结果进行对比，验证所建立桩承式路堤的离散元颗粒流模型的正确性，进而从细观角度对土拱效应的形成及演化规律进行研究。

1.1 室内模型试验简介

该模型试验中，模型槽由钢化玻璃和角钢制作而成，模型槽一面使用钢化玻璃，其余三面使用钢材制作(图1)。模型槽边长为0.9 m，高为1.3 m。模型试验尺寸与实际工程结构尺寸的比例为1∶10。路堤填土选用黄砂，填筑高度为0.5 mm，桩间土材料采用易变形的泡沫颗粒，厚度为0.3 m。在模型槽中设置三根钢制桩墙，桩间距为0.3 m，桩墙的尺寸为0.9 m×0.05 m×0.4 m，在桩墙周围填筑泡沫颗粒。该室内模型试验过程以及试验结果详见参考文献[14]。

图1 室内模型试验装置示意图Fig.1 The layout of the experimental device

1.2 桩承式路堤颗粒流数值模型的建立

基于室内模型试验的对称性，本文选取两个半桩及两桩之间的土体，建立了桩承式加筋路堤离散元颗粒流数值分析模型，如图2所示。该数值模型的尺寸为：桩高0.3 m，宽0.05 m，桩间距0.3 m，路堤高度0.5 m。路堤和桩间土颗粒均采用分层压实法进行分层填筑，每层厚度为100 mm(与室内模型试验过程一致)。模型槽及桩体均用颗粒流中的刚性墙(wall)模拟，以限制颗粒的运动；土颗粒、土工格栅均采用圆盘颗粒(ball)模拟。静载作用下桩承式路堤中的土拱效应研究，采用伺服机制在路堤顶面分级施加静载，施加的每级荷载为10 kPa。

1.3 模型参数的确定

在离散元颗粒流PFC模型中，路堤填料的细观参数采用试样尺寸为40 mm×80 mm(宽×高)的数值双轴试验反演试算获得，经过不断调试参数，直到数值模拟结果与试验结果基本相同。通过试算，最终确定路堤填料细观参数见表1，相应的数值双轴试验应力-应变数值模拟结果与试验结果对比图如图3所示。

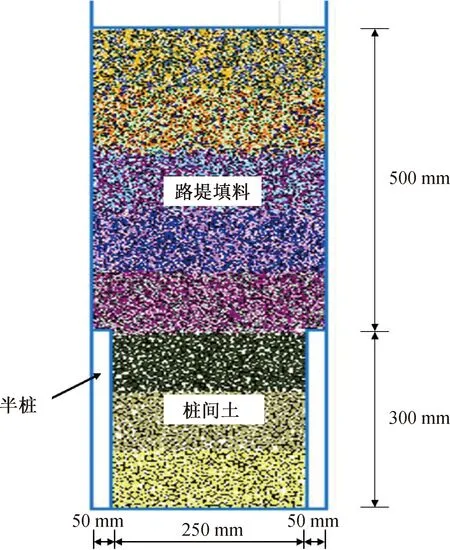
图2 桩承式路堤颗粒流数值模型Fig.2 The DEM model of piled embankment

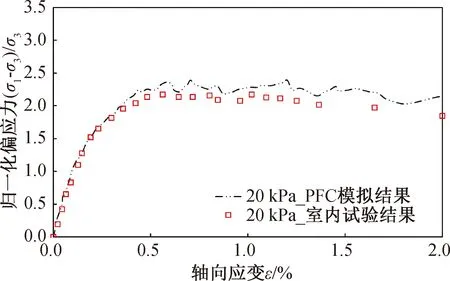
图3 数值双轴试验应力应变曲线Fig.3 The stress-strain curve of biaxial test for embankment material

采用尺寸为125 mm×50 mm(长×高)的数值压缩试验进行反演试算，确定桩间土的细观参数。具体步骤为：在125 mm×50 mm区域内生成粒径为3.5～5 mm且服从标准正态分布的颗粒。颗粒生成后，对试样顶部墙体施加恒定向下的速度进行加载，记录加载过程中顶部墙体的荷载-位移曲线，不断调试桩间土颗粒的细观参数，直到数值模型获得的应力-位移曲线与室内压缩试验得到的曲线相吻合，如图4所示。最终确定桩间土颗粒细观参数如表1所示。

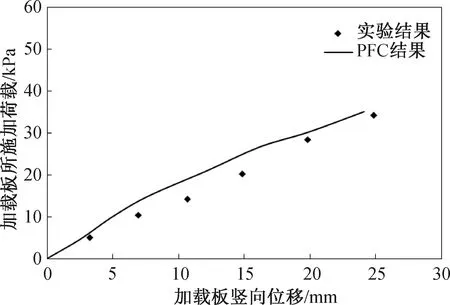
图4 桩间软土单向压缩试验离散元模拟结果与试验结果对比Fig.4 Comparison between the compression test by PFC and the experimental results

表1 PFC模型微观参数

1.4 模型验证

为验证本文离散元数值模型的正确性，将桩间距为0.3 m且路堤高度为0.5 m的平面土拱效应室内试验结果与PFC数值模拟结果进行对比分析，如图5所示。离散元数值模拟所得路堤中竖向应力的分布曲线与试验结果的曲线变化趋势相一致，两者误差约为2%～17%，从而验证了本文建立的桩承式路堤颗粒流模型的正确性。

图5 PFC数值模拟结果与试验结果对比分析Fig.5 Comparison between the numerical simulations and experimental results

1.5 数值模拟工况

为分析桩承式路堤中土拱效应的形成-演变规律，本次数值模拟建立了9个工况共25个离散元颗粒流模型。其中，工况1—5分析了在路堤自重应力作用下随着路堤高度的增加路堤中颗粒与颗粒间接触力的分布，从而分析路堤中土拱效应的发展过程。分析了工况6—9在逐级增加静态荷载作用下桩承式路堤中土拱效应的演变规律，具体工况如表2所示。

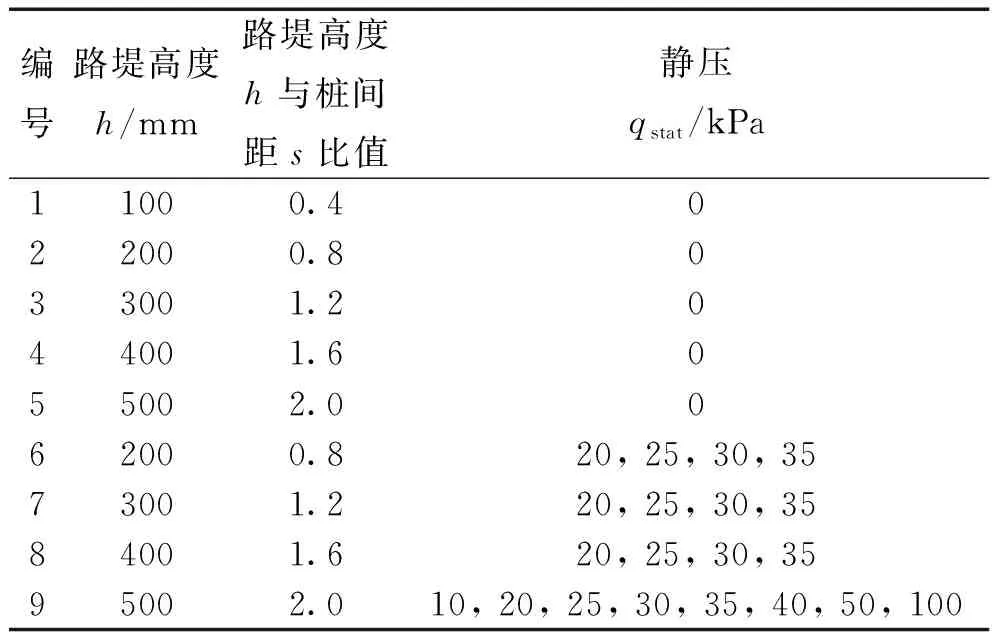
表2 离散元PFC数值模拟工况

2 静载作用下桩承式路堤中土拱效应演变规律

本文分别对路堤填料自重荷载作用及静载作用下路堤中的土拱效应形成及演变规律进行分析。首先，根据工况1、3、4、5分析了不同填筑路堤高度时路堤中颗粒间的接触力分布；其次，根据工况9对不同静载作用下路堤中竖向应力分布、应力缩减比SRR以及路堤中接触力的分布规律进行分析。

2.1 自重应力作用下桩承式路堤中土拱效应的形成-演变规律

图6为不同路堤高度情况下路堤中接触力的分布规律。图中接触力的大小按照相同的比例绘制，线条的粗细能够反映出接触力的大小，线条越粗表示接触力越大。从图6中可以看出，随着路堤高度的增加，路堤底部存在的接触力重分布现象逐渐明显，表现为在靠近桩顶处的接触力线条更加密集且粗，即接触力逐渐向桩上转移并集中，而软土上的接触力逐渐减小，桩承式路堤中的土拱效应逐渐得到发挥。当路堤高度h=100 mm时(h/(s-a)=0.5)，路堤中基本上没有出现接触力由路堤填土向桩上转移的现象，说明此时路堤中没有土拱效应产生，这与参考文献[14]中得到的“当h/(s-a) ≤ 1.0时，没有土拱效应产生”结论相一致。当路堤的高度增大至400～500 mm时(h/(s-a)的变化范围在2.0～2.5之间)，路堤中的强力链在软土的上方交错形成环形的拱结构，且该环形拱的两端位于相邻的两个半桩上，如图6(b)、6(c)中虚线所示，该土拱的形状与Hewlett 和 Randolph[9]提出的“半圆形土拱模型”相似，该半圆形土拱模型中应力由软土向桩上传递的现象主要发生在外拱与内拱之间所在的环形区域。从图中可以看出：随着路堤高度的增大，土拱的内、外拱高度均呈现增大的趋势。根据参考文献[14]推求的土拱效应外拱高度ho与内拱高度hi的理论表达式(公式(1)和(2))可以计算出：当路堤高度h=400 mm 与500 mm时，土拱的内、外拱高度分别为hi=96 mm、ho=184 mm(h=400 mm)与hi=100 mm、ho=185 mm(h=500 mm)，将理论公式的结果与图6(b)、(c)中的结果相比可知，理论公式计算出的内、外拱高度与数值模拟获得的内外拱高度的误差在1.0%～13.0%之间，从而验证了在桩承式路堤中，采用公式(1)与公式(2)计算平面土拱效应内、外拱高度的合理性。

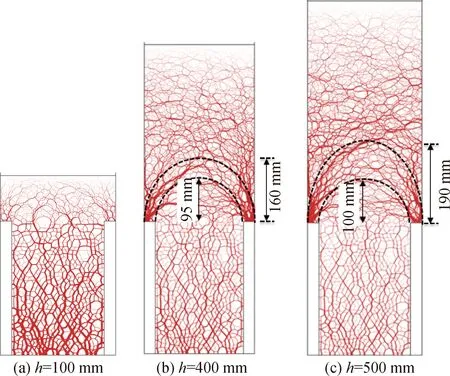
图6 路堤中接触力演变规律Fig.6 The evaluation of the contact force along the height of the embankment

(1)

(2)

式中：ho—土拱外拱高度，m；hi—土拱内拱高度，m；h—路堤高度，m；s—桩间距，m；a—桩帽尺寸或桩的直径，m。

2.2 静载作用下路堤中竖向土压力分布规律

为分析桩承式路堤中土拱效应完全产生时，路堤表面作用的静载qstat对土拱效应的影响，对桩间距s=250 mm，路堤高度h=500 mm的模型(h/(s-a)=2.5)逐级施加静载。图7为不同qstat作用时路堤中的竖向应力分布规律，其中qstat的取值范围为10～100 kPa。当qstat的变化范围为 10～50 kPa时，路堤中软土中心上方的竖向应力σqs沿着路堤高度呈现出三个阶段的变化规律，且不同qstat作用时的变化规律趋于一致：在距离路堤底部200 mm至路堤表面范围内，σqs沿着路堤深度逐渐增加；在距离路堤底部100～200 mm范围内，σqs沿着路堤深度急剧减小；在路堤底部至距离路堤底部100 mm范围内，σqs沿着路堤深度转而又出现增大趋势。可以看出，土拱效应作用在路堤底部—距离路堤底部200 mm范围内，并且随着静载的增加，该土拱效应作用的区域基本上没有发生改变，即路堤表面作用的静载qstat在10～50 kPa范围内变化时，对土拱内、外拱的高度基本上没有影响。 当qstat的变化范围在10～50 kPa时，桩上方的竖向应力沿着路堤高度逐渐增大，在土拱效应作用区域至路堤底部范围内，其增长变化幅值显著增大，从而使得桩上出现了较明显的接触力集中现象。可以计算出随着qstat的逐级增大(由10 kPa增大至40 kPa)，桩土应力比逐渐增大，相比qstat=10 kPa与qstat=30 kPa的结果可知，桩土应力比n增大了3倍左右。结合路堤中竖向应力的分布规律与桩土应力比的变化规律可知：在当静载在10～40 kPa范围变化时，桩承式路堤中土拱效应的发挥维持稳定且有增强的趋势。

图7 静载作用下路堤中竖向应力分布规律Fig.7 The distribution of the vertical stress of the embankment subjected to static load

当路堤表面的静载qstat增大至100 kPa时，路堤中的竖向应力分布曲线发生了变化，主要体现在距离路堤底部200 mm至路堤表面之间路堤中的竖向应力沿着路堤高度呈现弱化趋势，该趋势与陈仁朋等(2015)[15-16]分析的在静载下路堤中的竖向附加应力的分布规律相似。这与路堤表面作用较大的静载有关(例如qstat=100 kPa)，因为该静态荷载引起路堤中的竖向附加应力沿着路堤的深度呈现衰减弱化的趋势，相比于路堤的自重，该静载(路堤自重约10倍)对路堤中竖向应力分布的影响更大。因此，在路堤表面至距离路堤底部200 mm的范围内，路堤中竖向应力分布曲线与竖向附加应力分布曲线的规律相似。可以计算出此时桩土应力比n约是qstat=10 kPa情况下的80%， 桩土应力比n的减小说明了在qstat=100 kPa时，路堤中的土拱效应发生了退化，这将在后文中从接触力分布规律的变化作进一步分析。

2.3 静载作用下应力缩减比的变化规律

为进一步说明静态荷载作用下桩承式路堤中土拱效应的演变规律，对不同静载作用下的应力缩减比SRR的变化规律进行分析，如图 8 所示。在静载qstat作用时，SRR的计算表达式如公式(3)所示。从图8中可以看出，随着静载qstat的增加，应力缩减比呈现出两个阶段的变化规律。当qstat的变化范围为10～40 kPa 时，SRR随着qstat的增大而逐渐减小，这表明有较少的竖向应力由软土承担，而更多的荷载由桩来承担，桩承式路堤中的土拱效应逐渐增强。随着qstat的继续增大，SRR逐渐增大，当qstat由50 kPa增大为100 kPa时，SRR增大了约60%。与静载qstat在 10～50 kPa作用情况下相比，桩间软土承担了更多比例的竖向荷载，这表明此时路堤中的土拱效应发生了弱化，这与图7得到的结论相一致。

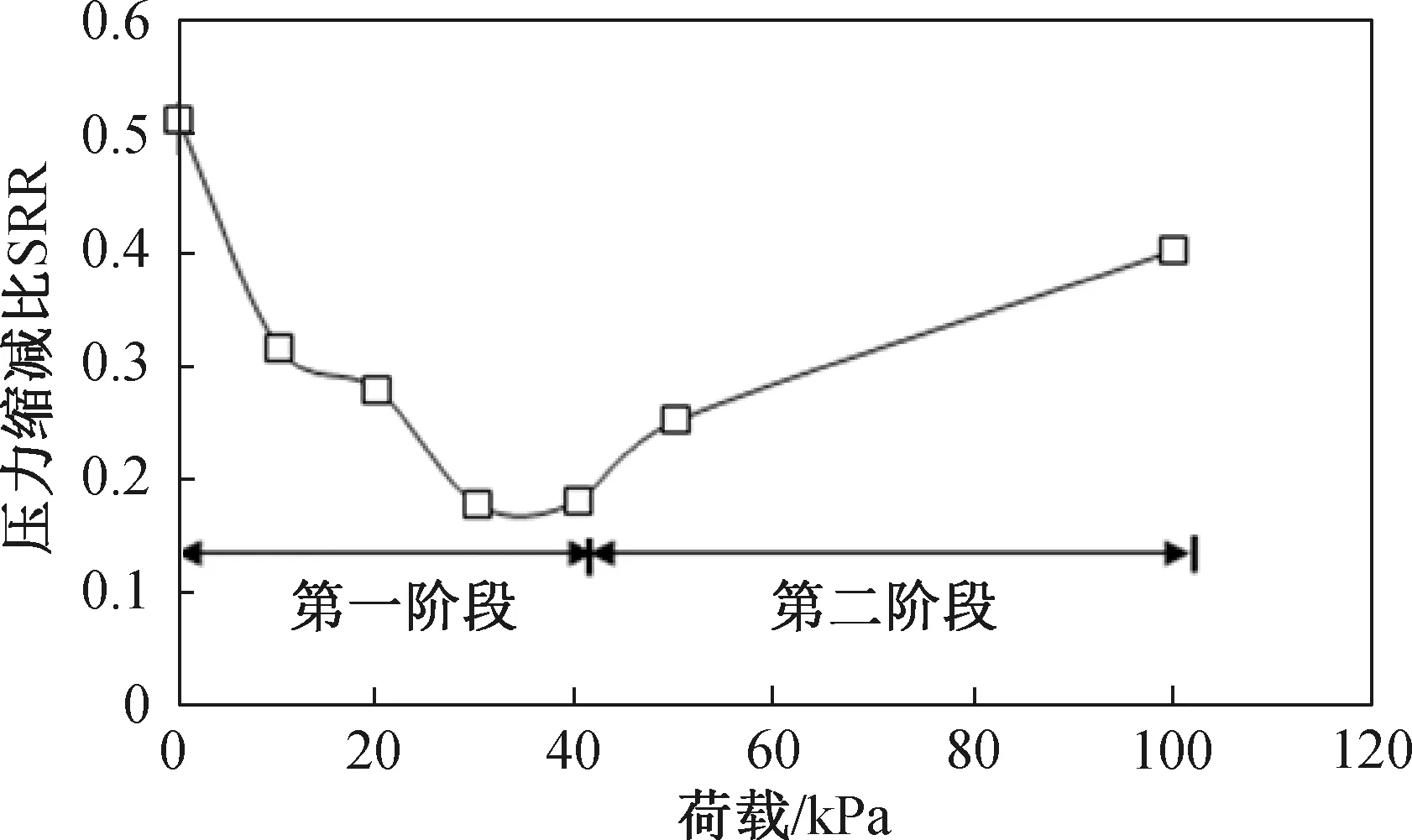
图8 静载作用下应力缩减比的变化规律Fig.8 The variation of the SRR for the embankment subjected to the static load

(3)

式(3)中：SRR为应力缩减比；γ为路堤的重度，kN/m3；σqs为软土表面上作用的竖向应力，kPa；qstat为路堤表面上作用的外加静力荷载，kPa。

2.4 静载作用下路堤中接触力分布规律

图9为不同静态荷载qstat作用下桩承式路堤中接触力的变化规律，基于该结果可以分析出施加不同静载作用对路堤中土拱效应的影响。从图9(a)与9(b)中可以看出，当qstat由10 kPa 增大至30 kPa时，土拱的外拱高度基本上没有发生变化，而内拱的高度有逐渐减小的趋势，说明土拱效应作用的区域在逐渐增大，在宏观上表现为应力缩减比SRR的减小，如图8中第一阶段所示。从图9(b)与9(c)中可以看出，当qstat由30 kPa 增大至40 kPa时，内拱、外拱的拱高均略有降低，在宏观上表现为SRR略有增大。从图9(d)可以看出，当qstat增大至100 kPa时，外拱的高度发生了明显的下降，根据参考文献[14]中软土表面作用的竖向应力表达式可知(公式(4))：当ho减小时，作用在软土表面上的竖向应力σqs增大，从而使得SRR的值变大，如图8中第二阶段所示。

从图9还可以看出qstat由10 kPa 增至100 kPa时路堤中接触力分布规律的变化。当qstat由10 kPa 增大至40 kPa时，桩承式路堤中的土拱效应发挥稳定，并且有增强的趋势；当qstat由40 kPa 增大至100 kPa时，桩承式路堤中土拱的内、外拱的位置均发生了明显变化，并有下降的趋势，说明在这个逐级加载的过程中，原来的土拱结构逐渐发生了退化，并且有新的土拱结构的形成，而新形成的土拱结构的作用区域在逐渐减小，在宏观上表现为应力缩减比SRR的增大，也就是软土承担竖向荷载的分担比呈现增大的趋势。

(4)

式中：σi为作用在内拱高度处的竖向应力，kPa；Kp为被动土压力系数。

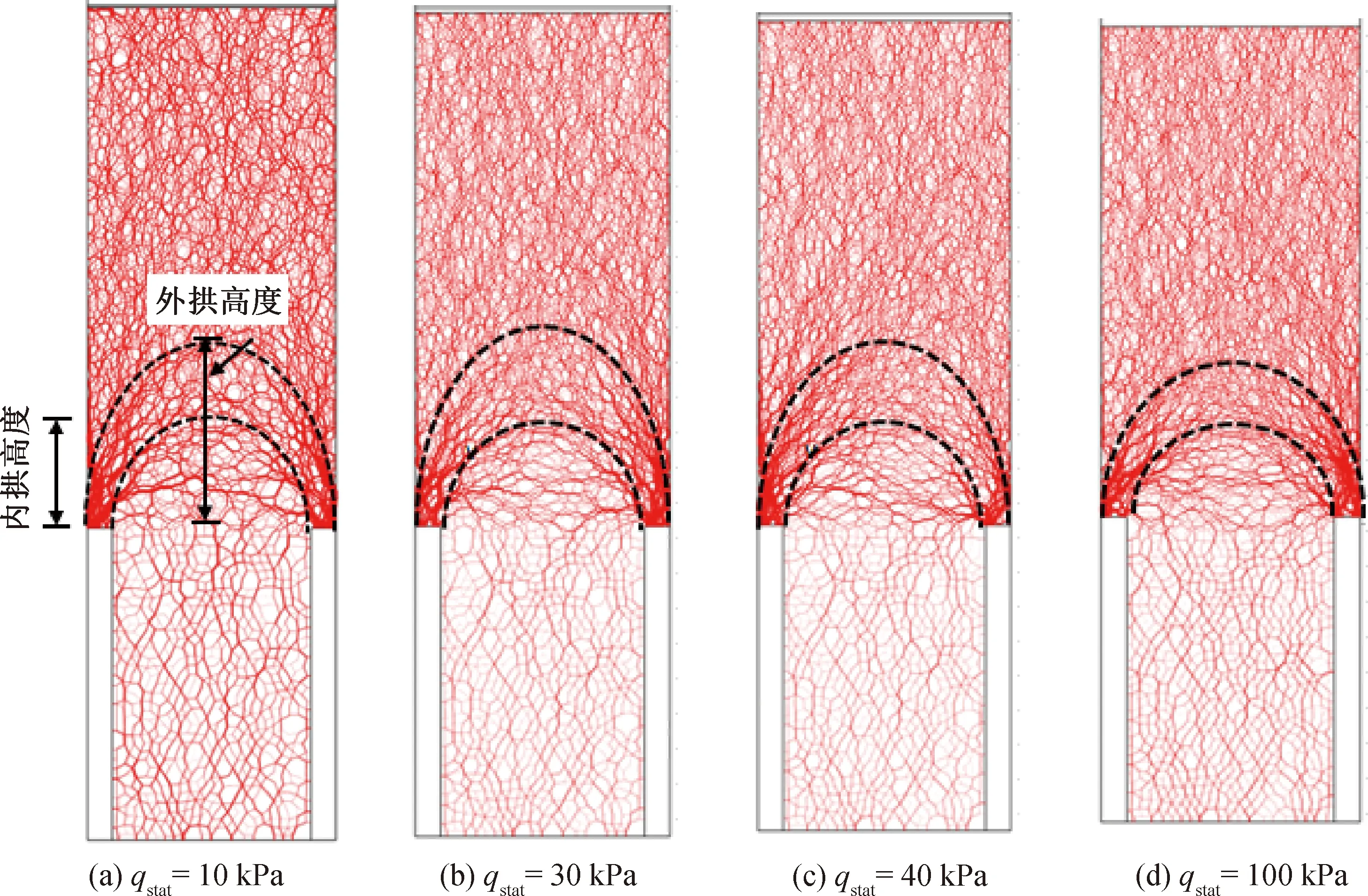
图9 静载逐级施加过程中路堤中接触力的变化规律Fig.9 The distribution of the contact force with the increase of static load

3 结论

本文根据室内模型槽试验建立了桩承式路堤的离散元颗粒流模型，并通过路堤的双轴试验和桩间软土的单轴压缩试验反演获得了路堤与桩间软土的微观参数。离散元数值模拟结果与室内模型试验的对比结果验证了本文建立的桩承式路堤颗粒流模型的正确性。基于该数值分析模型，从宏观和微观两个角度分析了路堤填料自重荷载作用及静载作用下桩承式路堤中土拱效应的形成及演变规律，本文的主要结论如下：

2)从路堤中竖向应力的分布规律、应力缩减比的变化规律以及路堤中接触力的分布规律三个角度分析了静载qstat作用下桩承式路堤中土拱效应的演变规律。当qstat由10 kPa 增大至40 kPa时，桩承式路堤中的土拱效应发挥稳定，并且有增强的趋势；当qstat由40 kPa 增大至100 kPa时，桩承式路堤中土拱的内、外拱的位置均有下降的趋势，原来的土拱结构发生了退化并有新的土拱结构形成，其作用区域逐渐减小，在宏观上表现为软土承担竖向荷载的分担比呈现增大的趋势。