17-4PH不锈钢热老化的磁多参数无损评估

褚英杰，孙 琦，李乾武，史芳杰，黄 飞，杨广宇

(1.福建宁德核电有限公司，宁德 352000;2.苏州热工研究院有限公司，苏州 215000)

17-4PH(05Cr17Ni4Cu4Nb)马氏体不锈钢因具有较高的强度和优异的耐腐蚀性能，被广泛应用于核电厂的高强度结构部件。17-4PH不锈钢在高温服役时会产生Cu颗粒析出、调幅分解、二次碳化物析出等现象[1]，导致材料的冲击功下降，硬度上升，脆性增加[2]，增加了材料的脆性断裂风险。因此，对17-4PH不锈钢的热老化评估具有重大意义。

不锈钢或者合金钢在热老化过程中，因微观组织的变化，其磁性能也会有相应的变化。BHATTACHARYA等[3-4]研究了磁巴克豪森噪声(MBN)与17-4PH不锈钢微观结构的关系。其将17-4PH不锈钢进行短时效热老化以后，发现Cu沉淀增多，且Cu的沉淀可有效降低巴克豪森噪声的峰值。GUPTA等[5]研究了不同时效阶段下蠕变对12CrMoWV高温合金钢的增量磁导率的影响，结果表明，在550 ℃与650 ℃的不同时效下，增量磁导率曲线呈现相反的变化规律。

由于17-4PH不锈钢热老化过程中微观组织变化的复杂，磁性无损检测在17-4PH不锈钢热老化评估的工程应用上具有一定的难度。笔者在研究马氏体不锈钢热老化后磁性变化规律的基础上，比较了不同磁参数无损检测方法的评估效果，引入人工神经网络，为沉淀硬化马氏体不锈钢热老化无损评估提供更可靠精确的方法。

1 试验方法

试验对象为某电厂的主蒸汽隔离阀阀杆，其材料为17-4PH不锈钢，其材料成分如表1所示。

表1 17-4PH不锈钢材料成分 %

为了模拟不同服役时间17-4PH不锈钢热老化的变化，同时缩短试验周期，在350 ℃下进行加速热老化试验,具体加热时间为0,100,300,500,1 000,2 000,3 000 h，共计7组样品。对加速热老化后的样品进行力学试验和磁参数测量。其中，冲击试验按照标准GB/T 229-2007的金属材料夏比摆锤冲击试验方法要求，在JB-W450E-L型试验机上进行试验；按照GB/T 231.1-2009的金属材料布氏硬度试验方法测试材料的布氏硬度；采用LakeShore公司的VSM(振动样品磁强计)平台测试磁滞回线，样品尺寸(长×宽×高)为1 mm×1 mm×3 mm；使用3 MA(多参数微磁显微组织应力分析仪)进行磁多参数测试，各磁参数如表2所示。

表2 3MA测得的磁参数

2 试验结果

2.1 力学试验结果

对加速热老化后的试验样品进行冲击试验与硬度测试，得到样品冲击功和硬度的变化趋势如图1所示。结果表明，17-4PH不锈钢在热老化后，冲击功呈下降趋势，而硬度呈上升趋势。大量研究表明调幅分解是导致17-4PH不锈钢脆性增加最主要的原因[6]。

图1 17-4PH不锈钢热老化后冲击功与硬度的变化趋势

2.2 磁参数测量结果

2.2.1 单一参数测量结果

通过VSM测得不同样品的磁滞回线如图2所示(1 T=104G, 1 emu=10-3A·m2)。由于17-4PH不锈钢是软磁材料，所以磁滞回线细长，磁滞损耗较小,即使在热老化3 000 h后，17-4PH不锈钢仍具有较低的矫顽力与磁滞损耗。这是因为材料在350 ℃下进行加速热老化，该温度远低于纯铁的居里温度[7]与常见铁碳化合物的平均居里温度[8]，所以材料的磁性不会发生明显的变化。17-4PH不锈钢样品的矫顽力与磁滞损耗随热老化时间的变化趋势如图3所示。

图2 不同热老化样品的磁滞回线

图3 不锈钢样品的矫顽力与磁滞损耗随热老化时间的变化趋势

由图3可知，材料的矫顽力最大波动范围不超过3 A·m-1，而磁滞损耗的最大波动幅度不超过0.000 7 J，同时呈现无规律变化趋势。3MA也对样品的矫顽力进行了测试，得到矫顽力随热老化时间的变化趋势(见图4)。由图4可知，矫玩力也呈无规律波动。

图4 矫顽力随热老化时间的变化趋势(3MA测试结果)

2.2.2 磁多参数测试结果

单一磁参数测试结果表明，17-4PH不锈钢在热老化过程中的矫顽力变化不大，而且呈现出无规律性的变化趋势，无法有效表征17-4PH不锈钢在热老化过程中力学性能的变化规律。基于磁多参数，通过建立人工神经网络模型，可以得到磁多参数与17-4PH不锈钢的硬度、冲击功之间的评估模型，并将模型评估的材料力学性能与试验实测的力学性能进行对比。

试验选取结构简单的双层前向型神经网络模型，输出层为线性神经元，输入测得的25个磁参数，选择隐藏层的激励函数为tansig函数(将磁参数作为n，代入函数)，其表达式为

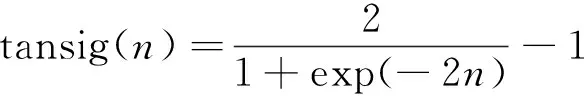
(1)

选取合适的隐藏层节点数，以L-M算法训练神经网络。冲击功与硬度的模型评估结果和试验结果的关系曲线如图5所示。

图5 冲击功与硬度的模型评估结果和试验结果的关系曲线

经过训练，可得到一个神经网络模型，将待评估材料的25个磁性参量作为输入，输出结果为材料的力学性能评估结果。

结合图3与图5可知，即使在单一参数无规律的情况下，也可通过大量的磁多参数检测数据，应用人工神经网络，建立起精度较高的评估模型。

3 分析与讨论

3.1 隐藏层节点数量对模型的影响分析

隐藏层节点数对模型的影响有：① 节点数会影响模型的运算速度，节点数越多计算时间就越长;② 节点数越多，拟合效果越好，超过一定数目，会出现过拟合现象。因此，需要选取合适的节点数目以保证良好的拟合效果。

图6为节点数分别为10，30，50，70时拟合误差柱状图(强度表示误差在每个区间分布的统计相对数量，无量纲)，在10节点和30节点时，误差分布呈正态分布。对于10节点模型，较多误差均分布在0误差线两侧；在拟合节点超过30以后，误差多数分布在0误差线左右；50节点与70节点模型的误差分布类似，此时再增加节点数的效果已经不明显了。为了进一步研究节点数增加对拟合效果的影响，可分析拟合度随隐藏层节点数增加的变化趋势(见图7)。

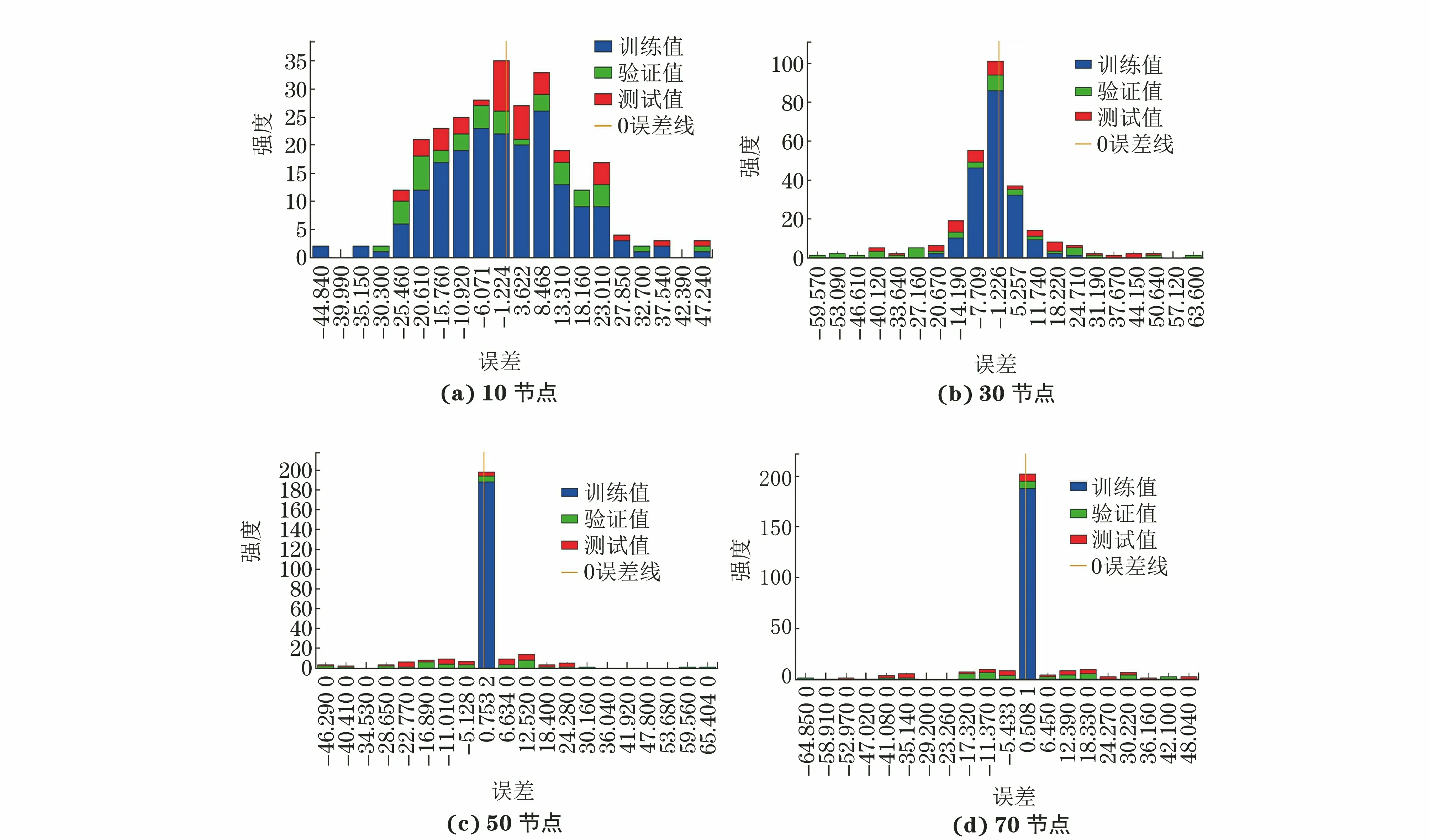
图6 不同隐藏层节点数的误差柱状图

图7 拟合度随隐藏层节点数的变化趋势

一般来说，选取节点数可根据输入层的节点数大致确定，而多数情况下需要研究节点数与拟合效果之间的关系来得到最优化的神经网络模型。由图7可知，节点数越多，训练值的拟合效果越好，但是对新出现的样本的适应性却下降，无法较好地拟合，也就是说隐藏层节点数在超过一定限值后，神经网络的拟合效果反而会下降。

3.2 训练算法对模型的影响分析

常用的训练算法有：L-M算法；贝叶斯正则化算法；量化共轭梯度算法。L-M算法使用一种广泛的非线性最小二乘算法，通过对待测参数作线性近似，将问题转化为最小二乘问题，因而计算量相对较少，可很快地达到收敛状态；贝叶斯正则化在基于L-M算法的基础上，更新优化权重和偏置，生成普适性更强的神经网络；量化共轭梯度算法基于共轭方向，具有收敛快，占用内存小等特点。笔者分别从算法运算速度，拟合效果两方面综合比较3种模型。

选择隐藏层节点数为40，分别以3种算法建立神经网络模型，比较3种算法的特性，对比结果如表3所示。

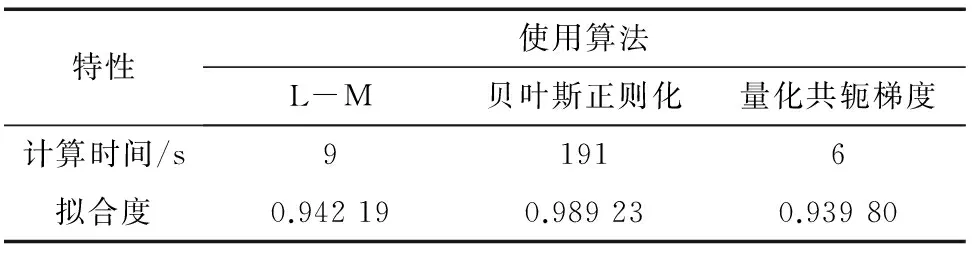
表3 3种算法的对比

综合分析来看，L-M算法计算所需时间较短，且模型的拟合度较高，因此L-M算法在实际应用中更为实用。贝叶斯正则化迭代次数需要到1 000次时结果才收敛，而L-M算法和量化共轭梯度算法分别在60次和7次迭代后收敛，在一定程度上保证了结果不会过拟合。

基于磁多参数，可以利用人工神经网络，可以给出磁性参数与力学性能之间的描述模型，且评估速度快。

4 结论

(1) 17-4PH不锈钢在热老化后，冲击功下降，硬度上升，说明热老化导致其脆性增加。

(2) 单一的磁参数测量结果表明，17-4PH不锈钢在350℃下热老化后，其矫顽力、磁滞损耗均在小范围内波动，且呈无规律变化，说明单一的磁参数测量方法不适用于评估17-4PH不锈钢的热老化。

(3) 基于磁多参数，应用人工神经网络，可建立评估17-4PH不锈钢热老化的模型，其评估效果较好，可以解决单一磁参数无法评估17-4PH不锈钢热老化的问题。在应用人工神经网络建立17-4PH不锈钢评估模型时，需要选取合适的网络节点数及合适的算法，可有效提升建模效率，得到较好的精度。