管道低频弯曲模态导波频散曲线的测定

杨志春,伍文君

(1.海装驻武汉地区第一军事代表室，武汉 430060；2.武汉理工大学 能源与动力工程学院，武汉 430063)

管道广泛应用于工业生活的各个领域，如何对其进行有效监测是广受业内关注的问题。声学检测是当前管道检测的主要方法之一。声波在管道中传播具有多模态和频散等特性，这给信号的分析带来了极大的困难，因此开展管道声学检测的前提是弄清声波在管道中的传播特性，即测定管道的导波频散曲线。计算管道导波频散曲线的方法有很多，包括理论推导[1-2]和数值计算[3-5]等。理论计算得到的频散曲线仍然需要试验测定来进行验证。此外，管道的材料特性参数也很难准确地确定，只有通过试验才能获得准确的管道导波频散曲线。

以MDPE(中密度聚乙烯)管道为研究对象。MDPE管道常用作埋地水管，其常见的故障是开裂泄漏。已有研究表明，泄漏造成的管道振动主要为低频振动(振动频率小于1 kHz)。MDPE管道在低频范围内存在有轴对称的纵向导波模态、轴对称的扭转导波模态和非对称的基础弯曲模态。文章对MDPE管道低频弯曲模态的导波频散曲线进行了试验测定。

1 理论频散曲线

文章采用经典的欧拉伯努利梁理论[6]计算管道的低频弯曲模态导波频散曲线。将管道类比成截面为环形的特殊梁，其低频弯曲振动即可认为是这一特殊梁的弯曲振动。根据经典梁理论[6]，有

(1)

式中:x为沿梁长度方向的位置坐标；t为时间；V为梁上某点的垂直位移，是位置x的函数；E为杨氏模量，I为梁截面的惯性矩，其二者的乘积(EI)表示梁的弯曲刚度；m为梁单位长度的质量；Q(x)为作用在梁垂直方向上的外力。

因为计算的是梁在自由状态下的振动，所以Q(x)=0。m和I按其定义，分别计算为

m=2πRhρ，

(2)

I=πR3h

(3)

式中:R为管的平均半径；h为管的厚度；ρ为管的密度。

MDPE管的尺寸及材料性能参数如表1所示，计算得到的理论频散曲线如图1所示。

表1 MDPE管的尺寸及材料性能参数

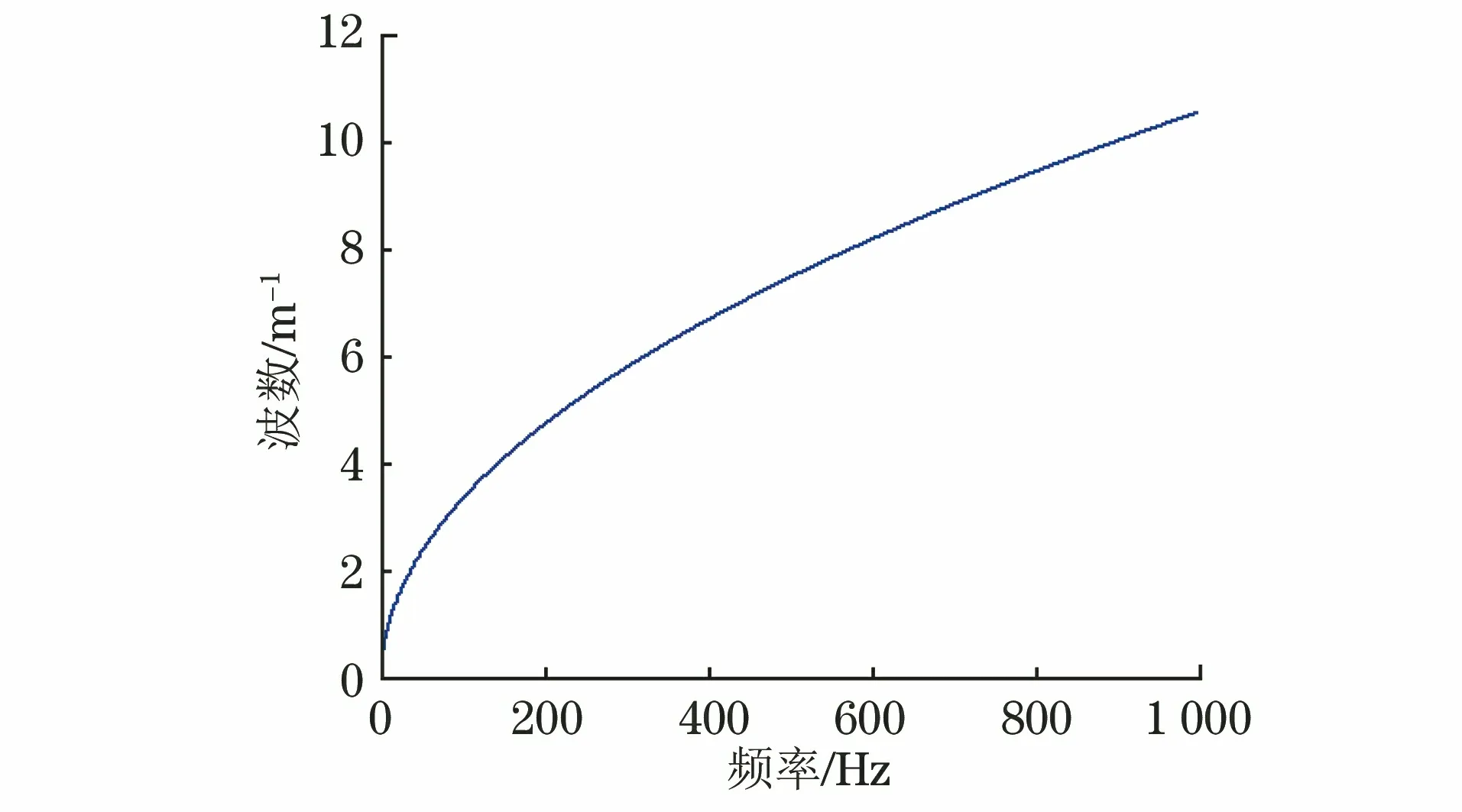
图1 MDPE管的理论频散曲线

2 试验测定

2.1 试验设置

试验布置示意如图2所示，将长约6 m的MDPE管悬挂，激振器置于管的左端用于激发管的振动，3对加速度传感器等间距布置在管壁上用于检测管的振动，传感器的间距分别设置为75,150 mm。每对加速度传感器包含2个传感器，分别布置在管圆周方向的对称位置。由于管的弯曲振动在圆周方向对称位置上产生的位移是刚好相反的，因此将这两个传感器接收到的振动信号相减，便可以消除轴对称模态，从而提取出更纯净的弯曲模态。试验装置外观如图3所示。激振器的激励信号采用Chirp信号，信号的频率为10 Hz～1 000 Hz。

图2 试验布置示意

图3 试验装置外观

2.2 信号处理方法

管道长度有限，且处于自由状态。激振器激发的导波沿管的长度方向传播，当遇到管端时，便会发生反射。因此，管中同时存在正向和反向传播的导波，也即

p(x,t)=p+ei(ωt-kt)+p-ei(ωt+kt)

(4)

式中:p(x,t)为管长度方向上的压力分布;p+ei(ωt-kt)和p-ei(ωt+kt)分别为正向和反向传播的导波;ω和k分别为导波的角频率和波数。

对于3个等间距布置的加速度传感器，假设其间距为L，位置坐标分别为x0-L，x0和x0+L，则有

p(x0-L)=p+e-ik(x0-L)+p-eik(x0-L)

(5)

p(x0)=p+e-ikx0+p-eikx0

(6)

p(x0+L)=p+e-ik(x0+L)+p-eik(x0+L)

(7)

将式(5)(7)进行数学整理，得

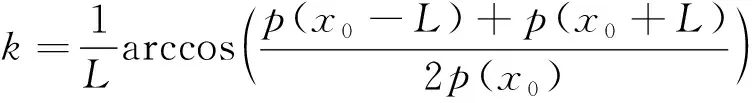
(8)

式(8)描述了波数与频率之间的关系，也就是导波的频散曲线方程。

2.3 试验结果分析

传感器间距为750 mm和1 500 mm时，未去周期性和去周期性的测定频散曲线和理论频散曲线分别如图4,5所示。由式(8)可知，计算得到的波数具有周期性，而且传感器的间距越大，周期越多，需要做更多的去周期操作。从图4,5可以看出，去周期性后得到的频散曲线都比较平滑，只在低频以及600 Hz～700 Hz内出现了跳变。

图4 未去周期性和去周期性的测定频散曲线和理论频散曲线(L=750 mm)

图5 未去周期性和去周期性的测定频散曲线和理论频散曲线(L=1 500 mm)

不同传感器间距的测定频散曲线如图6所示，可见，传感器间距为1 500 mm时的频散曲线更平滑，方差更小。这意味着在实际测试中，传感器间距应取大一些，以便得到更优结果。

图6 不同传感器间距的测定频散曲线

从图6还可以发现，试验频散曲线与理论频散曲线在低频段拟合得较好，而高频段则存在偏差。这一偏差可能是经典欧拉伯努利梁理论在高频段不适用造成的。

3 结语

对MDPE管道低频弯曲模态频散曲线进行了测定。等间距布置3组加速度传感器检测管道的振动，提取出了该管道的弯曲模态频散曲线。试验结果证明了该方法的有效性，可以测得较为平滑的管道频散曲线，且传感器间距越大效果越好。此外，试验测定的频散曲线与采用经典欧拉伯努利梁理论计算得到的频散曲线在低频段拟合良好，在高频段则偏差较大。