基于GARCH-VaR模型的中国铁矿石期货市场风险度量的有效性研究

姚爱萍，丁晓文

(1. 西南大学 经济管理学院，重庆 400715 ；2. 西南大学 智能金融与数字经济研究院，重庆 400715)

一、引言

铁矿石期货，是以铁矿石为标的物的期货品种，利用期货合约的标准化特性，制定的商品期货合约。铁矿石期货的推出与发展，为全球铁矿石供应商、贸易商以及终端用户规避市场风险提供了途径。作为工业大国，中国一直是全球最大铁矿石的进口国和消费国，据海关总署披露，2020年，中国进口铁矿石11.7亿吨，同比增加9.5%；对应金额8228.7亿元人民币，同比增加17.4%。两者均创下历史新高，但中国在铁矿石价格方面一直缺乏与消费地位相匹配的影响力。

2020年8月7日，中国钢铁工业协会和大连商品交易所组织部分钢铁企业召开专题会，计划在现有交割制度上分批增加一些矿种作为可交割品牌，这些矿种符合交割规范、为市场广泛接受，旨在更好地为钢铁产业服务，由此铁矿石价格走势进一步引起社会各方的关注。在现期新冠肺炎疫情对全球经济影响的大背景下，国际各类资产纷纷下跌，大宗商品也经历了宽幅震荡，其中以石油为甚。原油与铁矿石作为全球两种重要的大宗商品，它们的价格走势具有较高的相关性，然而在沙特发动原油价格战后，在国际原油跌破30美元/桶的情况下，铁矿石价格依旧坚挺，这无疑对铁矿石期货投资者、中国钢铁行业的发展等产生巨大影响。鉴于此，本文将GARCH-VaR模型用于铁矿石期货市场风险的比较度量研究，选取铁矿石期货主力合约收盘价经过处理后的数据建立GARCH-VaR模型，通过似然比(LR)检验对比不同分布下模型的精确度。这对期货投资者投资策略的制定、期货交易所保证金的设置以及监管部门对期货市场的合理监管标准的制定等都有重要意义。

二、文献综述

(一)期货市场有效性研究

Garbade和Silber(1983)[1]首先运用实证方法分析商品与现货市场价格之间的关系，形成了著名的GS模型，后续大量的研究文献实现了GS模型的扩展。Engle和Granger(1987)[2]提出并发展了协整理论，为市场有效性检验提供了一种新的方法，有效地解释了价格序列的非平稳问题。在此基础上，Gay等 (2009)[3]利用误差修正模型分析了基于高频数据的天然气期货价格发现函数，发现期货价格与现货价格长期一致性。Milunovich和Joyeux(2007)[4]利用协整检验分析了欧洲棉花期货的现货价格和期货价格序列，并发现不同期限的二者存在非平稳序列。

国内学者对于期货市场的有效性也做过诸多研究。鲁瑞荣(2005)[5]通过对大豆和小麦的期货与现货价格的拟合检测，得到大豆期货市场短期有效而小麦无效的结论；蒋舒与吴冲锋(2007)[6]则在前两个品种的基础上，新增了3个主力品种铜、铝和胶，通过Johansen协整检验、VaR框架下的方差分解进行实证研究，认可了中国期货市场的有效性。除此之外，还有对具体期货市场分析，如沪深300股指、黄金等期货市场的研究[赖文炜和陈云(2015)[7]，季俊伟等(2019)[8]]，研究结果皆表明所研究的期货市场已经实现了弱势有效。

(二)期货市场风险度量研究

在期货市场的风险度量方面，最初的风险管理工具是JP Morgan公司于1994年提出的VaR模型(在险价值模型)，Wipplinger和Philippe(2007)[9]在他们的文章中详细地给出了该模型的建立过程，并明确了模型存在的局限性。然而金融时间序列数据往往都表现出尖峰厚尾的特征，基于此Bollerslev(1986)[10]将GARCH模型与VaR模型联合起来，先利用GARCH模型计算出收益率序列的条件异方差，再运用到VaR值的计算中。Kupie(1995)[11]提出了基于失败率的回测方法，初步实现了对VaR模型有效性的验证。Alexander等(2013)[12]则认为过去一些精确的VaR估计值建立在特定的GARCH族模型基础上，实证结果则获得了在多个视野和显著性水平下的准确的GARCH-VaR预测。

鉴于我国的期货市场属于新兴市场，对其理论研究较少，主要偏重于实证分析。在这些实证研究中，很多学者都用到了GARCH-VaR模型，杨怀东等(2010)[13]在模型的基础上加入一种新的综合性流动指标，建立了动态交易保证金模型；刘向丽和常云博(2015)[14]则是将模型用于度量沪深300股指期货的总体风险。除了GARCH-VaR模型，Realized HAR GARCH模型也受到广泛应用，蔡光辉和项琳(2020)[15]考虑到沪铜期货收益所表现的长记忆性，而采用HAR结构提升模型的预测性能，为风险度量和预测提供了新思路。此外还有对不同风险指标估计精度差异的对比实证分析，如王鹏等(2012)[16]运用Backtesting分析对中国金属期货市场进行研究。

(三)铁矿石期货市场研究

铁矿石期货市场研究主要集中在期货与现货价格之间的关系以及与期货价格的定价上。Indriawan等(2019)[17]对我国三种重要的工业金属期货展开研究，分析表明螺纹钢和铜期货在信息效率方面的可比性，并且要高于铁矿石，还发现铁矿石与螺纹钢期货之间存在着双向联系。Yves Jégourel(2020)[18]回顾了世纪之交以来金融化对铁矿石市场的影响，并解释了中国铁矿石期货市场的存在，重点分析了这种金融化对于铁矿石市场的未来乃至采矿业的启示。Jingjing Tuo和 Fan Zhang(2020)[19]提出一种混合的EEMD-戈鲁模型和一种新的数据重构方法，探索中国铁矿石期货和现货市场的价格风险和波动相关性。他们认为中国铁矿石期货市场的远期价格无法充分反映国内铁矿石期货市场的变化，因而无法充分传播国内铁矿石市场信息。国内研究一般在期货和现货价格的波动分析的基础上做出延伸，基于GARCH、MSVAR等模型，或是加入了市场情绪探究对二者的影响[李莉(2017)[20]，王萌和樊燕萍(2019)[21]]；在与定价有关的研究方面，各学者运用不同的模型与分析方法将国内铁矿石期货的国际定价能力作为研究焦点，虽然定价影响力较弱，但对其引导能力逐年增强做了肯定[邓超和袁倩(2016)[22]，胡振华等(2018)[23]，朱学红等(2018)[24]]。另外，潘昭帅等(2020)[25]则梳理了铁矿石主流的定价工具并做比较研究，指数定价仍被视为最重要的定价工具。

通过对国内外文献梳理后发现，国外风险量化与管理的相关理论体系更加系统与完善，并远远领先于国内的研究，现今广泛使用的一些模型与方法大都是国外的研究成果。对比国内的研究虽然在某些方面有些创新，但更多的是对国外研究成果的应用，并且由于国内外金融市场发展状况的巨大差异，导致一些风险度量方法并不适用于我们的研究。本文的创新之处在于将国外的风险度量模型应用于我国的铁矿石期货市场，基于对日收益率的不同分布假设来找出最适合度量我国铁矿石期货市场的模型，这对铁矿石期货市场风险管理的进一步研究有重要意义。

三、我国铁矿石期货市场发展现状

在已经具备成熟市场条件的情况下，我国于2013年10月18日在大连期货商品交易所推出首个铁矿石品种合约，国内所有铁矿石供应商皆可参与，随着交易量的上升，会逐渐吸引国际资本参与国内铁矿石期货的交易，进而提升铁矿石定价机制的话语权。2018年以后，铁矿石期货市场加快了对外开放的步伐，继3月底启动原油期货全球化贸易之后，大连期货交易所于同年5月4日推出以人民币结算的铁矿石期货，这意味着铁矿石期货成为第二个迈进国际化的期货品种。铁矿石对于我国工业发展的重要性不言而喻，但其需求主要依赖进口这一趋势中长期内不会改变。

近年来，铁矿石期货在人民币国际化的进程中也贡献着力量，2020年5月，宝钢股份与澳大利亚力拓集团在区块链技术的加持下完成一笔总值逾1亿元的人民币跨境结算，其交易标的就是铁矿石。毫无疑问，大宗商品的结算易于促进人民币国际化，这也意味着在该领域内国内企业话语权的提高。

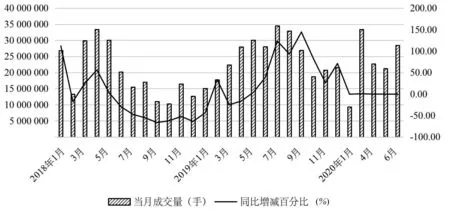
图1 2018年1月—2020年6月大连商品交易所铁矿石期货成交量与同期增减百分比

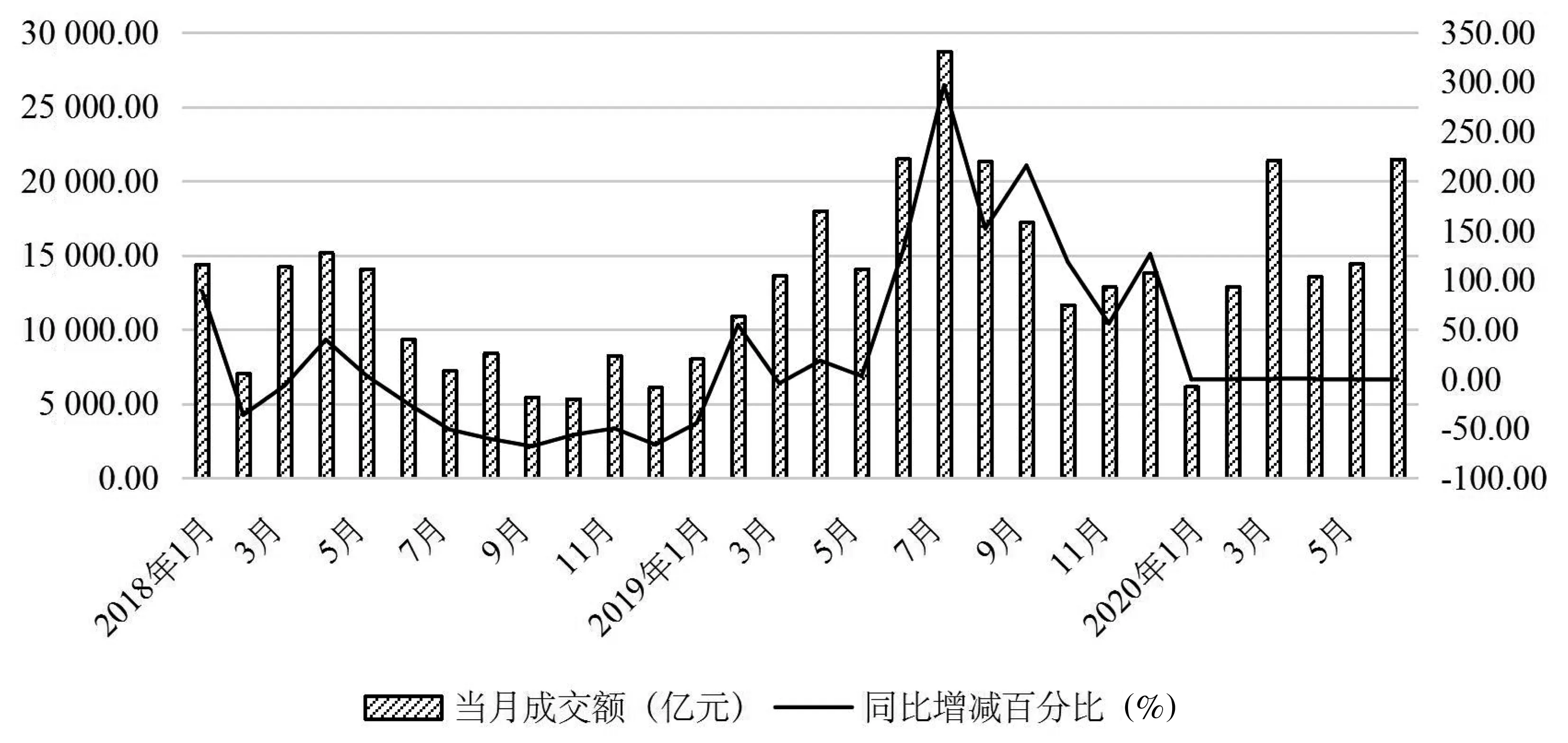
图2 2018年1月—2020年6月大连商品交易所铁矿石期货成交金额与同比增减百分比

根据大商所的数据显示，铁矿石期货在2019年的累计成交总额为19.87万亿元，同比增长72.39%，成为国内成交额最大的商品期货。如图1、图2所示，是2018年1月—2020年6月大连商品交易所铁矿石期货成交量与成交金额，在成交量提升幅度没有超越以往高点的情况下，2019年的铁矿石期货成交金额创下了历史新高，其成交量与成交金额皆在7月达到顶峰，在2020年1月之前同比增减百分比都处于震荡的状态。

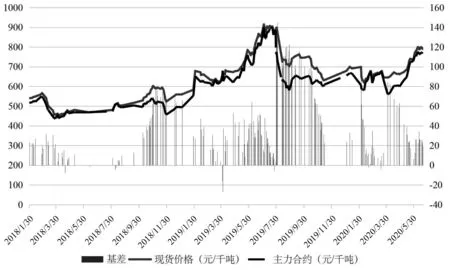
图3 2018年1月30日—2020年6月19日铁矿石现货价格、主力合约价格及基差情况

从图3可以看出，自2018年1月30日以来，铁矿石的现货及主力合约价格上涨明显，并于2019年7月突破900元/千吨，并在高位震荡了月余，且基差在此期间的绝大部分时间都是正值。此外，值得关注的是，在经历了短时间的大幅下降后，从2020年4月开始，铁矿石需求端持续攀升，截至6月中旬，铁矿石期货也从4月初的542元/千吨上涨至752元/千吨。多种因素的作用使得铁矿石的价格高位震荡，在海外供应端收缩的情况下，国内对铁矿石的需求不降反升，国内钢铁行业的巨额利润早已使得海外矿山盆满钵满，中国在进口铁矿石市场的势力不可小觑。

四、铁矿石期货收益率波动及风险的实证分析

(一)数据的收集及统计分析

本文从大连期货交易所官网(http://www.dlfe.com.cn/)的每日铁矿石期货收盘价(除周末与节假日外)，时间从2018年1月30日至2020年6月19日共205个铁矿石期货主力合约收盘价，用对数的一阶差分rt=lnxt-lnxt-1对收盘价进行处理，得到日收益率。

1.时序图

本文利用Eviews8.0软件，对处理后的数据进行描述性统计分析，首先是收益率序列时序图，如图4所示。

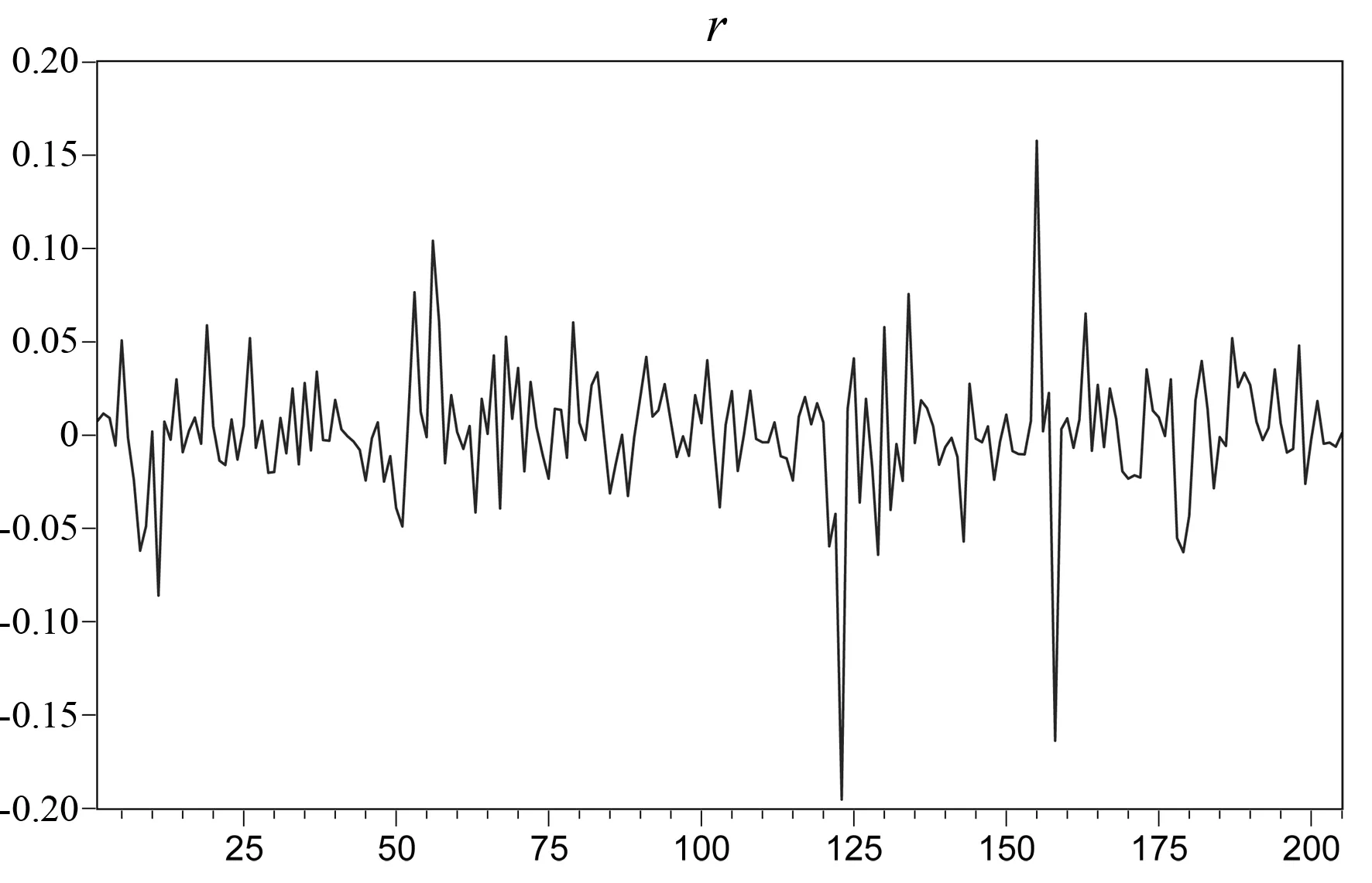
图4 收益率时序图

从图4可知，收益率在0处上下波动，总体来说波动范围较稳定，但也有几处波动异常。第一处波动出现在2019年7月29日至2019年8月12日，第二处波动出现在2019年11月12日至2020年2月13日。前者主要是铁矿石期货出现远期合约交换和远期升水，因为国内铁矿石期货是10%的保证金交易，再加上消息面和基本面的影响，一天内可能有100%左右的价格波动，导致出现期货价格的涨停板。后者的波动则是新冠肺炎疫情的影响，国内封锁了大部分的对外出口项目，导致铁矿石价格出现程度比较大的波动。

2.直方图

由图5可以看出，序列的均值是0.001367，标准差为0.034270，最小值为-0.195321，数据的偏度为-0.870576，其值小于0意味着序列分布有长的左拖尾，峰度是11.87556，要高于正态分布3的峰度值，说明其日收盘价的收益率序列具有“尖峰厚尾”的特征；Jarque-Bera统计量值达到了698.7702，同时P值为0，故拒绝该对数收益率序列服从正态分布的假设。对于这里的尖峰厚尾，本文之后运用GED分布和t分布来拟合。通过以上检验结果，可以分析得出收益率分布显著地不服从于正态分布，而是出现了具有尖峰厚尾现象，所以本文选择使用GED分布与t分布来拟合，并且用QQ图来检验。这里以t分布为例，如图6所示，是在该收益率序列服从t分布的假设下使用QQ图的检验结果。

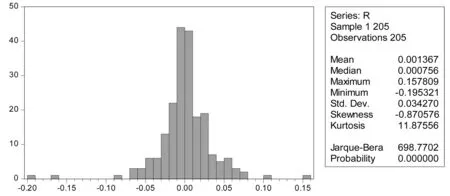
图5 收益率直方图

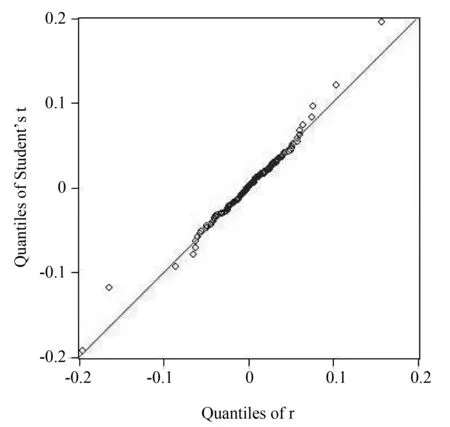
图6 t分布下的收益率序列QQ图

据QQ图所示，t分布描述得很好，在随后的模型建立过程中，我们以残差服从t分布与GED分布的假设确定参数来完成GARCH模型的建立。然后研究残差平方序列的自相关性，为此建立残差平方序列的均值方程，并用Ljung-Box检验确定残差平方序列的相关性。经检验，其值均小于0.05，因此拒绝原假设，判定残差平方的时间序列具有自相关，具有ARCH效应。

3.平稳性检验

接下来对铁矿石期货收益率序列进行ADF检验，结果如表1所示。

表1 收益率序列的ADF检验结果

根据表1中的结果，铁矿石期货收益率序列的ADF值为-13.62005，小于1%、5%、10%显著性水平下的临界值，对应P值接近0，这表明收益率序列不存在单位根，拒绝序列随机游走的原假设，认为序列是平稳的，说明我们建立GARCH模型进行实证部分的研究过程是有效的。

4.相关性检验

本文通过杜宾-沃森(D-W)和自相关检验进行序列相关性检验，由杜宾-沃森(D-W)检验的结果，铁矿石期货合约收益率序列的D-W值是2.003920，约等于2，因此我们可以认为该收益率序列的残差不存在序列相关性。接下来再对该收益率序列进行相关性检验，结果见表2。

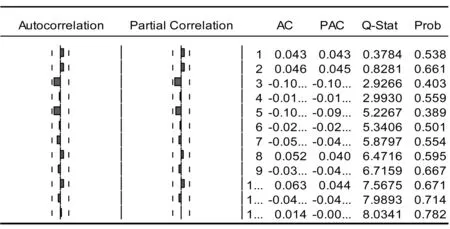
表2 收益率序列的自相关检验结果

由表2可知，自相关和偏自相关系数基本都落在两倍的估计标准差内，且Q-stat统计量对应的P值均大于0.05，故该序列在5%的显著性水平上不存在显著的相关性，因而可将均值方程设定为白噪声，设立模型rt=πt+εt。

(二)建立GARCH模型

1.ARCH-LM检验

由于金融时间序列常存在异方差，因此在建立GARCH模型之前，还需判断收益率序列是否存在ARCH效应，我们依旧使用Eviews8.0来进行下列的检验过程，首先对滞后一阶的收益率序列进行最小二乘估计，然后对其残差序列进行ARCH-LM检验。

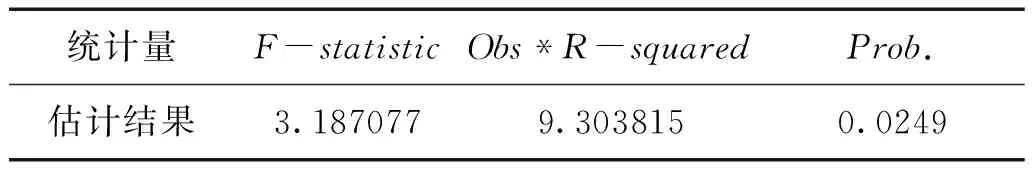
表3 收益率序列的ARCH-LM检验结果

由表3可知，在5%的显著性水平下，收益率序列的F统计量所对应概率小于0.05，故拒绝收益率序列不存在ARCH效应的原假设，从而存在条件异方差。

2.GARCH模型的建立

由上述分析检验可知，铁矿石期货的收益率序列符合我们建立GARCH模型的条件。再由描述性统计量的分析结果可知，序列存在明显的“尖峰厚尾”特征，正态分布不能恰当描述其特点，所以本文只给出了GARCH模型在t分布与GED分布下的估计结果。

首先将收益率序列GARCH模型的均值方程设定为白噪声，然后在t分布和广义误差分布下，比较GARCH(1,1)、GARCH(1,2)、GARCH(2,1)及GARCH(2,2)模型产生的AIC和SC值的大小，据此选择对应的模型。根据GARCH(1,1)、GARCH(1,2)、GARCH(2,1)及GARCH(2,2)模型的拟合结果，得出表4。

基于以上四个不同参数的比较结果，综合来看选择GARCH(1,2)-t与GARCH(2,1)-GED模型来拟合扰动方程，具体结果见表5。

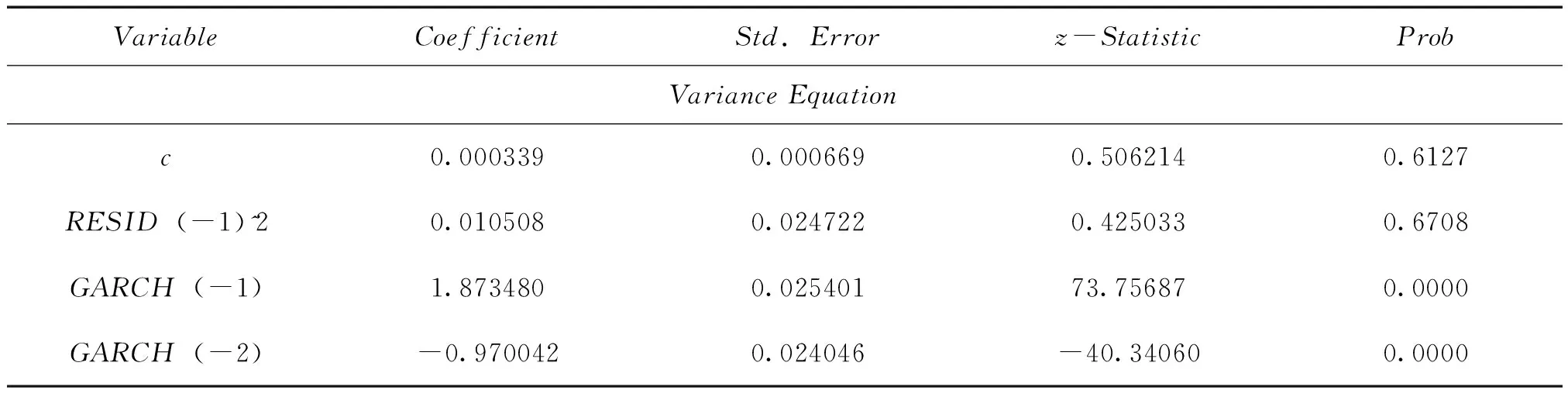
表5 收益率序列的GARCH(1,2)-t模型估计结果

根据表5所示的估计结果得出GARCH(1,2)-t模型的均值方程与扰动方程如下：

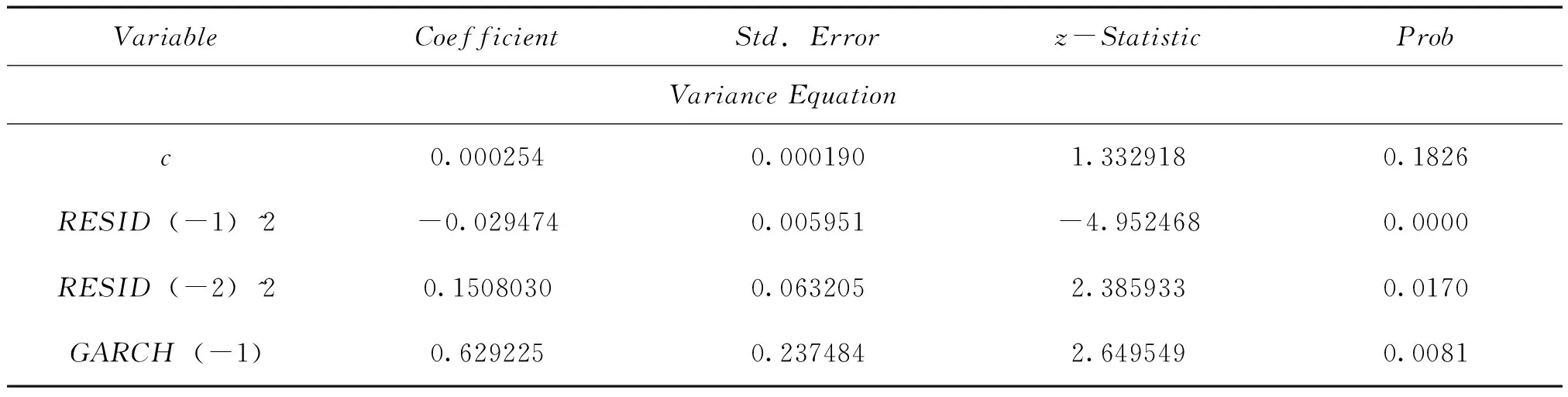
表6 收益率序列的GARCH(2,1)-GED模型估计结果

根据表6所示的估计结果得出GARCH(2,1)-GED模型的均值方程与扰动方程如下：

接着还需要对上述所建立的GARCH模型再次进行ARCH-LM检验，观察模型是否消除了残差序列ARCH效应，结果如表7所示。

表7 模型建立后的ARCH-LM检验结果

由表7可知，在95%与99%的置信度下都不能拒绝原假设，所以本文建立GARCH(1,2)-t模型与GARCH(2,1)-GED模型都成功消除了残差序列的条件异方差性。

(三)基于GARCH模型的VaR计算与分析

1.VaR的计算

将GARCH模型族与VaR的计算结合起来，也是计算VaR值的一种相对有效的新思路。在Eviews8.0软件中可以通过对金融资产的收益率序列建立适当的GARCH模型，来完成对收益率序列条件方差的预估，再将其转化为收益率序列的方差，代入VaR值的公式中，比如计算相对VaR的公式：

便可求得VaR的值。以GARCH-N为例，假设收益率与均值方程的误差项均服从正态分布，则GARCH模型计算相对VaR值可以使用如下公式：

VaRt=pt-1zασt

其中pt-1为前一时刻股票收盘价格；zα为标准正态分布下的临界值，通过查表可得，在置信度为95%的水平下，取zα=1.645；σt是根据GARCH模型求出的收益率序列的条件方差。在已知t-1时刻信息集Ft-1的情况下，收益率序列的条件均值和条件方差为：

μt=E(rt|Ft-1)

然而正态分布下的GARCH-VaR模型忽略了股市收益波动的集聚现象，不能反映收益率序列的峰值和厚尾特征，会对VaR的计算精度造成影响。所以我们在计算GARCH-VaR模型时可以考虑其他的分布，本文的研究我们考虑的是使用t分布与GED分布来模拟收益率变化。计算公式也很简单，在上述正态分布计算公式的基础上，将zα更改为t分布下在置信水平分位数Tα或广义误差分布下的分位数Gα，从而求出t分布与GED分布下的VaR值。

按前文所述，这里对VaR值的计算采用如下公式：

VaRt=ZασtPt-1

计算铁矿石期货的收益率序列在95%与99%的置信度下，基于GARCH(1,2)-t与GARCH(2,1)-GED模型的结果，其中Zα是t分布与GED分布在不同置信度水平下对应的分位数；σt是收益率序列的条件方差，再经过开方得到的标准差；Pt是代表金融资产在时刻t的价值，这里我们采用的是铁矿石期货在研究区间内的收盘价。除此之外，还需要在t分布与GED分布下的自由度，在上述通过Eviews8.0的模型建立过程中可得到两种分布下的自由度，分别为T-DIST.DOF=2.191430、GED PARAMETER=0.866964，再有关于不同分布下对应分位数的确定，对此整理出表8：

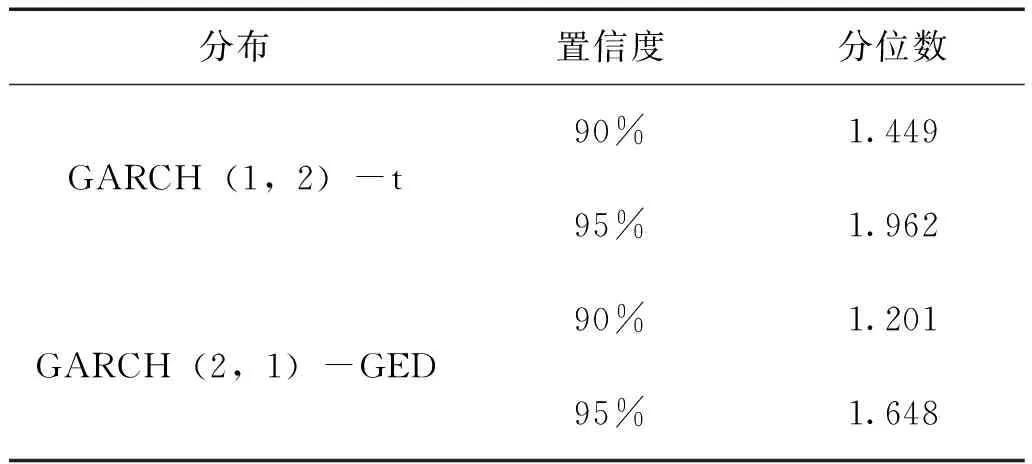
表8 不同分布下的分位数

通过表8给出的分位数，以及在上述过程中得到的GARCH(1,2)-t与GARCH(2,1)-GED模型所预测到的条件异方差序列，代入计算公式即可预测出不同置信度水平下的VaR值。

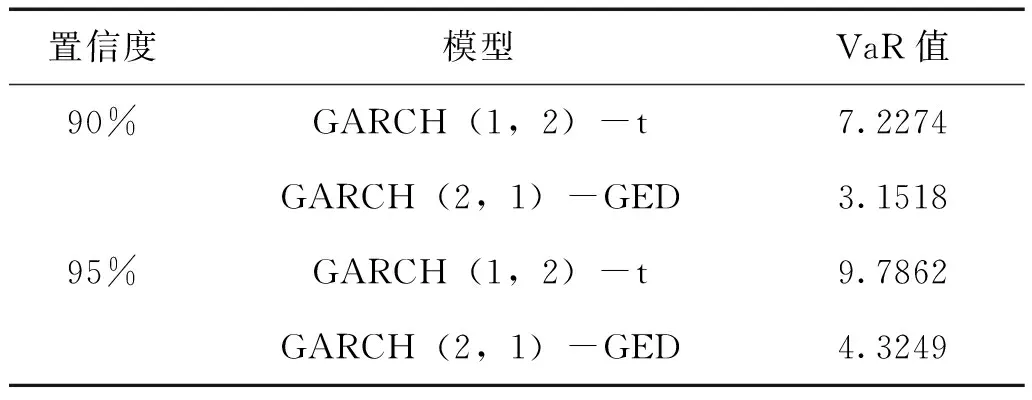
表9 不同模型与分布下预测的平均日VaR值

由表9可以得到：无论是在哪一种置信水平下，GARCH(2,1)-GED模型所预测的VaR值要小于GARCH(1,2)-t模型所预测的VaR值。

2.VaR的检验

VaR模型可以加深监管部门和金融机构对当前金融风险的了解，但是模型的建立是否准确，测量精度高不高，还有待检验。Kupiec的失败频率检验法就是其中应用最广泛的一种，主要思想是得出VaR值超出实际损益的概率，对数据样本进行返回检验，计算溢出天数。基本操作流程如下：

(1)判断模型是否有效——首先采用似然比来预测和判断；

(2)判断模型是否准确——对比失败率的大小来判断。

在每个单日失败的概率不会对其他单日造成影响的情况之下，我们可以将Kupiec失败频率检验当作一个独立的伯努利实验，这里引入虚拟变量Nt，当金融资产真实盈亏大于VaR值时，视为实验失败，记Nt=0；当真实盈亏小于所计算出的VaR值时，视为实验成功，记Nt=1，以此来进行回测检验，计算出溢出天数N，具体表述如下：

若要计算置信水平1-c下的VaR值，还要根据溢出天数与样本容量的比得到失败频率p，原假设与备择假设分别为H0:p=1-c、H1:p≠1-c，下面给出似然比检验：

LR=-2ln[(1-p*)T-N(p*)N]+2ln[(1-p)T-N(p)N]

其中T表示样本容量，N表示失败天数，p*表示置信水平。和其他统计量相同，LR在不同的置信水平下的临界值不同，若计算得到的LR值小于临界值，则接受原假设，说明VaR模型是相对准确的，反之则反。此外，Kupiec还给出如表10所示的接受区间：

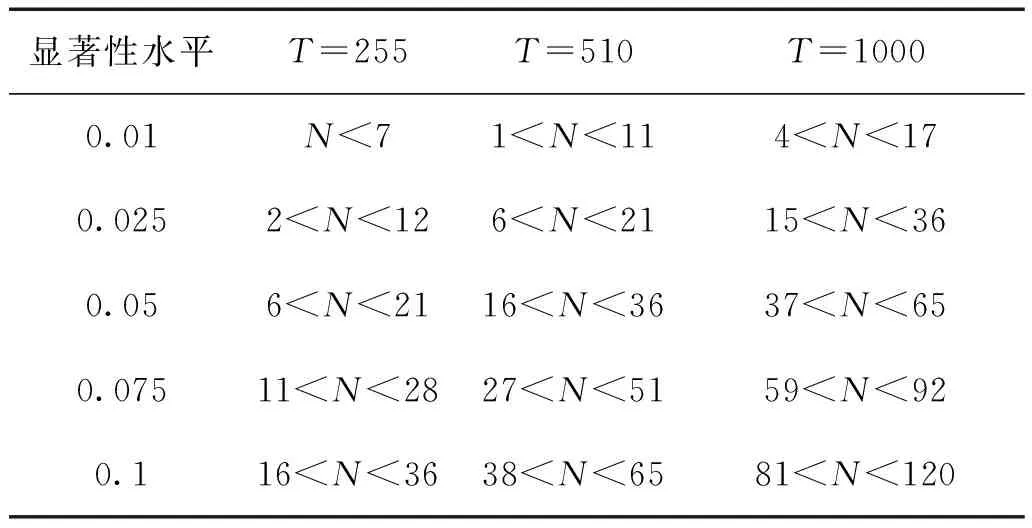
表10 Kupiec检验置信域

通过表10可以与实际数据得到的失败天数作比较，当失败天数处于置信域时就不能拒绝原假设，反之则反。

按照前述内容介绍的似然比检验：

LR=-2ln[(1-α)T-N(α)N]+2ln[(1-p)T-N(p)N]

其中T表示样本容量，N代表失败天数，理论上来说，N服从概率为p*=1-α贝努利分布。似然比检验的统计量LR～χ2(1)和其他统计量相同，若计算得到的LR值小于临界值，则接受原假设，说明VaR模型是相对准确的，即

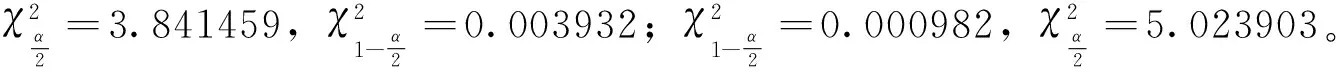
将T=204,P*=α(α=0.1,α=0.05)分别代入LR统计量的公式计算得到统计量的值，表11给出铁矿石期货在不同分布下的VaR值的失败率及失败天数的有效性检验结果。

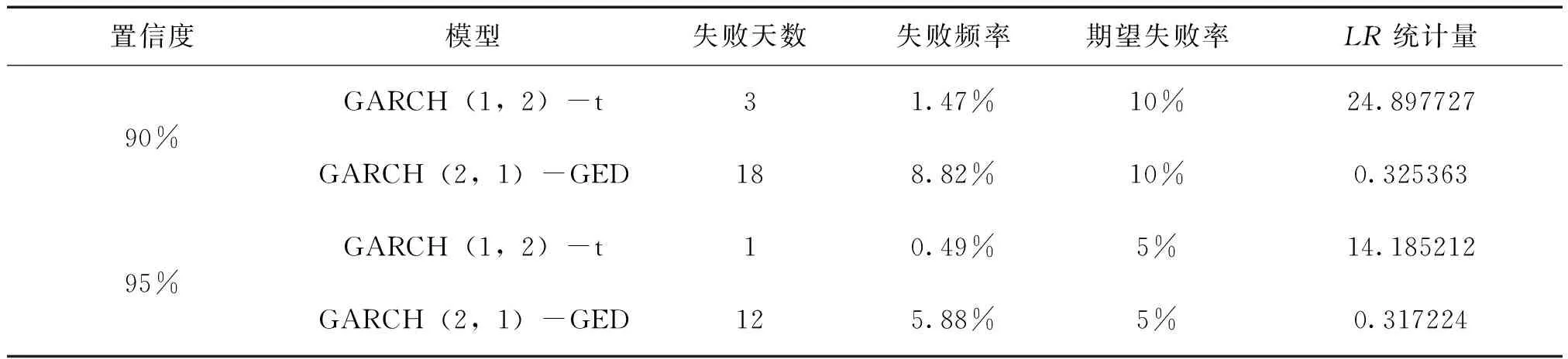
表11 不同分布下的VaR值有效性检验

3.结果分析

在前述内容中我们已经通过计算得到：在90%的置信度下，不能拒绝原假设的范围是0.003932≤LR≤3.841459；在95%的置信度下，不能拒绝原假设的范围是0.000982≤LR≤5.023903。观察表11可以得到：

(1)从失败天数与失败频率的角度来看，GARCH(1,2)-t模型下得到的失败天数较少，导致失败频率与期望失败率相差甚远，我们认为在t分布假设下对铁矿石期货市场风险的度量模型过于保守使得精确度有较大偏差；反观GARCH(2,1)-GED模型基于失败天数得到的失败频率与期望失败率相差不大。从该角度我们初步认为GARCH(2,1)-GED模型对铁矿石期货收益率的精确度更高。

(2)从LR统计量的计算结果来看，通过GARCH(1,2)-t模型得到的LR值在两个不同的置信度下均落在了拒绝域，通过GARCH(2,1)-GED模型得到的LR值在两个不同的置信度下均落在了接受域，通过整理得到表12：

表12 VaR值的LR检验结果

在90%与95%置信度水平下的GARCH(2,1)-GED模型均通过了检验，我们有理由认为该模型能够较好地描述铁矿石期货日收益率时间序列，较为准确地度量铁矿石期货市场的风险，预测效果较好，可以作为风险管理的依据。为进一步评价两个模型对风险的度量情况，我们更进一步地给出关于所预测的VaR值序列的描述性统计分析结果，如表13所示：

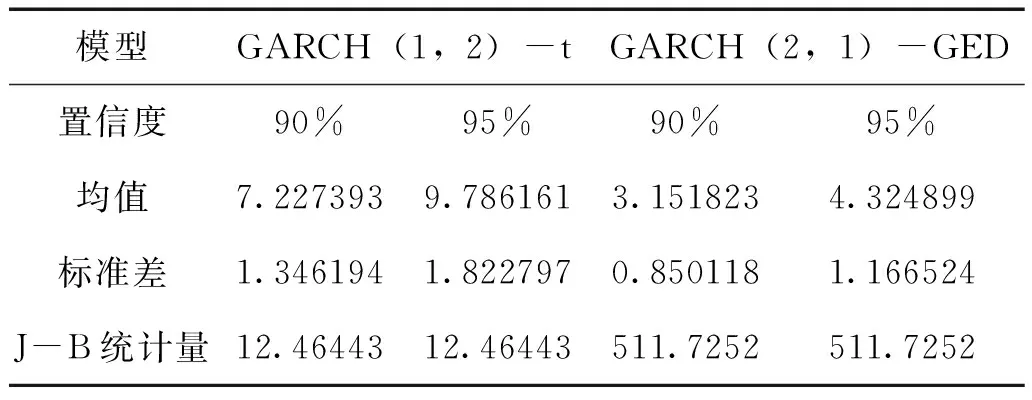
表13 GARCH模型的VaR值描述性统计分析

均值反映了VaR值的平均水平，标准差反映了VaR值的偏离均值的程度，由上表的描述性统计结果可知，GARCH(1,2)-t与GARCH(2,1)-GED模型基于10%与5%的置信水平下，在均值和标准差两个方面均存在差异。其中在均值方面，GARCH(1,2)-t模型在两种置信度水平下的预测结果要大于GARCH(2,1)-GED模型所预测结果的2倍，说明后者对预期损失程度的减少，而前者高估了铁矿石期货市场的风险；在标准差方面，GARCH(2,1)-GED模型的结果要小于前者，这表明模型所表达的VaR偏离均值的程度也在下降。整体来看，GARCH(2,1)-GED模型要优于GARCH(1,2)-t模型，GARCH(2,1)-GED模型对市场的估计更加接近预期风险值。

五、研究启示

根据以上研究结论，得出如下启示：

(1)将VaR方法纳入风险管理体系中。结合国外经验及本文的实证结果，将GARCH-VaR模型纳入铁矿石期货风险管理体系中具有现实意义。

对于期货投资者来说，可以利用VaR值来衡量期货合约未来可能发生风险的情况，通过评估所持有期货合约的风险值来调整期货投资组合，将风险控制在自己的承受范围之内，达到分散和规避风险的目的，规划好投资策略降低盲目性导致的损失。

站在期货交易所的角度，VaR方法可用来设定保证金水平，其对期货交易所和投资者双方都很重要。若设定值过高，在违约概率降低的同时会增加投资者的交易成本，交易信用虽然得到了维护却吸引不了投资者；若设定值过低，会导致杠杆效应增大，违约概率增大，不利于整个期货市场的健康发展。

对监管部门来说，重视VaR方法并将其引进到金融监管中，缩小与发达国家在期货市场风险管理水平方面的差异，为适应监管部门应对金融市场波动对监管技术提出了更高要求。

(2)进一步发掘和完善期货市场。中国的铁矿石期货市场距离成熟状态还有很长一段路程，与发达国家的差距较大，各方都应该发掘期货市场在资源配置、价格发现等功能方面做出努力，提高在预警及抵御风险方面的能力，争取有朝一日我国铁矿石期货市场在世界舞台上的定价权和话语权。

(3)强化铁矿石现货市场的有效性。期货市场的成熟程度建立在现货市场是否发达的基础之上，任何市场都要按照市场机制和价格规律运行，政府应努力建立健全相关法律法规，促进铁矿石市场化。

(4)建立有效的铁矿石价格波动预警体系。在当下信息化时代，不妨利用大数据对所收集的有关铁矿石价格信息来掌握铁矿石价格的波动情况，随着国际间交流程度的加深，我国受国际市场的影响程度会越来越深，我们需要一个有效的国际铁矿石价格预警系统。

(5)注重高级金融人才的培养。进一步落实教育兴国、人才强国计划，培养高素质的风险管理方面的人才，服务于我们的监管部门与各大金融机构，填补我国金融人才缺口。