气垫围裙连接结构数值仿真及改进设计

王露寒，唐文勇*，徐圣杰,2，袁昱超

1 上海交通大学 海洋工程国家重点实验室，上海 200240

2 中国船舶及海洋工程设计研究院，上海 200011

0 引 言

气垫船具有良好的两栖性、越障性以及快速性，能适应大多数的海岸环境，是实现两栖登陆作战的重要舰艇之一，在军事上有着广泛的应用前景。气垫船与普通刚性船舶最大的区别在于船底设有气垫围裙结构，通过与风机结合，可在船底与运行表面之间形成高压气垫，从而将船体与运行表面分离，因而可以在沼泽、冰区及湍流等复杂的环境下实现高速航行[1]。然而，气垫船复杂的工作环境造成柔性围裙张力常处于剧烈变化的状态，再加上围裙系统与船体连接多借助复杂的螺栓连接结构，存在结构形变剧烈、应力响应复杂以及循环应力显著等问题，造成围裙与围裙连接结构寿命较短，制约了气垫船在恶劣工作环境下的使用。

为此，众多学者针对围裙连接系统展开了深入研究。Ma和Sullivan[2]讨论了裙布几何形状、囊压比等对围裙结构响应的影响，提出的线性柔性围裙动力学理论为围裙连接系统的设计优化奠定了基础。Chung等[3]将该理论扩展至非线性领域，分析了大型气垫船非线性升沉运动的特征，指出了围裙系统中的高应力区域并给出了设计优化建议。Lavis和Forstell[4]将计算机辅助设计方法应用于围裙设计，有效缓解了围裙的指端应力与交变载荷，极大提高了围裙的使用寿命。郑楠[5]在实船使用的基础上，对各种连接件与裙布连接后制成的试件进行了静拉伸及疲劳强度的系列试验，发现合适大小的螺栓组可以改善围裙的裂纹扩展。周佳等[6]利用有限元仿真方法，对气垫围裙受拉后的应力和破坏位置的分布情况予以了讨论，得到了增大夹制预紧力可以有效提高组件整体承载能力的结论。

尽管国内外学者已经对围裙连接系统展开深入研究，围裙的寿命已得到很大提高，但在气垫船的实际使用过程中，仍然出现了连接区域铰链、船体板以及销轴等关键构件的破坏失效现象，说明现阶段围裙与船体连接结构的设计依靠规范经验公式并不准确。其主要原因在于，经验公式无法准确表达围裙连接结构中螺栓连接和复杂构件接触等因素对结构承载能力的影响，而数值仿真方法可以通过构建实体模型真实地考虑不同构件间的相互作用关系对结构的影响。因此，本文将针对围裙连接结构的特殊性，提出考虑螺栓连接、多构件复杂接触以及围裙与金属构件相互作用等因素的三维有限元模型构建方法，然后利用有限元软件对某气垫船艏部区域的围裙与船体连接结构进行数值仿真，模拟不同工况下连接结构的应力分布情况，最后根据计算所得结果，提出针对现有构件设计的改进方案，从而提高气垫船围裙连接结构的安全性和使用寿命。

1 围裙连接结构模型构建方法

目前，围裙连接结构采用的是与合页结构类似的设计，相关构件包括与船体连接的艇体铰链、与围裙连接的围裙铰链，以及串联两种铰链的销轴及压板等。该结构最大的特点在于，利用螺栓结构实现多构件的连接涉及大量的构件接触问题。其中，螺栓连接结构由螺栓与螺母构成，两者通过螺纹进行连接，具有较强的几何非线性特征，产生的螺栓预紧力会直接影响结构的应力响应，因此螺栓与螺母的紧固方法是构建螺栓结构模型的重要内容之一；而当构件之间处于紧密接触状态时，力的传递通过接触面完成，因此接触面的设置会对计算结果产生影响。由于柔性围裙易发生大变形，因此构建模型时，需要根据接触构件间材料属性的差异设置合理的接触面参数。

1.1 模型几何参数

围裙连接结构核心的铰链组合（围裙铰链和艇体铰链）在结构中重复出现，故只需选取局部结构进行计算即可，但需要考虑合适的计算范围以降低边界设置的影响。分别构建不同长度艏部连接结构的有限元模型并进行垫升工况与极端工况下的承载计算，最终选择了边界设置影响小且计算效率高的3对铰链组合范围进行艏部围裙连接结构研究，相应结构的实际应用区域及具体模型如图1所示。其中，船体板尺寸为340 mm×70 mm×3 mm，压板尺寸为300 mm×50 mm×5 mm，围裙尺寸为300 mm×70 mm×10 mm；螺栓采用M10-40型号，销轴半径为4.5 mm；铰链厚度均为5 mm，转圆部分内圈半径为5 mm；艇体铰链和围裙铰链这2种铰链搭扣部分的长度为49.5 mm。

1.2 构件材料属性

船体板采用铝合金，密度为2.7×10-9t/mm3，杨氏模量为7.1×104MPa，泊松比为0.34，屈服强度为195 MPa。螺栓、螺母、艇体铰链、围裙铰链以及压板均由不锈钢制成，其密度为7.8×10-9t/mm3，杨氏模量为2.1×105MPa，泊松比为0.30，屈服强度为205 MPa。气垫围裙材料选用增强纤维橡胶布，其力学性能参数设置与文献[7]一致。

图 1 艏部连接结构示意图Fig.1 Schematic diagram of bow's connection structure

1.3 网格划分与接触定义

船体板、围裙以及压板均进行开孔处理，然后根据位置关系进行装配，以保证铰链与销轴预接触。计算模型采用C3D8R实体单元构建，需要考虑网格尺寸对计算结果的影响。根据各构件的尺寸特征，构建粗网格、细网格以及局部细化网格等多种网格进行承载计算。为兼顾计算效率与结果精度，船体板与压板的最大网格尺寸为4mm×4mm×1.5mm（2层），围裙铰链与艇体铰链的最大网格尺寸为 2mm×2mm×1.3mm（3层），围裙的最大网格尺寸为 3mm×3mm×2.5mm（4层），螺栓与螺母的最大网格尺寸为 3mm×3mm×2.5mm，销轴的最大网格尺寸为1 .5mm×1.5mm×1.5mm。螺栓孔、铰链与销轴的接触区域均需要进行网格细化，单元尺寸多控制在1～1.5 mm之间。具体的三维精细化模型如图2所示。

图 2 艏部连接结构精细化模型Fig.2 Refined model of bow's connection structure

为了较真实地模拟螺栓结构预紧过程，本文参考文献[8]，采用绑定约束模拟了栓轴与螺母的接触状态，即假设螺母不发生松动，但有效栓轴长度仍可发生变化。各构件间涉及大量的接触非线性问题，为避免出现结果的不收敛，法向力和切向力分别通过罚函数与库伦摩擦模型施加，摩擦系数取为0.05[6]。不同类型的构件接触还需要考虑不同的接触面设置。金属构件间的接触应选择区域面积小的作为接触从面，并允许接触面间的相对位移；而考虑围裙与金属构件的接触时，则应选取易变形的围裙表面作为接触从面并限制接触面间的相对位移，以使围裙与构件始终处于紧密接触的状态，从而有效降低由单元穿透引起的数值误差。

1.4 边界条件设置

为保证围裙承拉时与船体板平行，对连接结构进行螺栓预紧时，在船体板上端面和左右端面、压板左右端面以及销轴右端面施加固支边界条件。船体板、压板和销轴均为连续结构，围裙承拉时需保证结构在y轴方向的位移不受约束。具体的边界条件设置如表1所示，采用的坐标系统如图1(b)所示。表中， θx， θy， θz分别为对应坐标轴的转角。

1.5 载荷施加

围裙连接结构承拉过程的模拟可以分为螺栓预紧和围裙承拉2个阶段。螺栓预紧时，预紧力施加于螺栓的根部剖面。基于螺栓标准扭矩及预紧力速查表[9]，螺栓预紧力大小设为7 500 N。围裙承拉时，螺栓预紧力不再作用，保持有效栓轴长度不变即可。为保证围裙均匀受拉，将围裙张力以分布载荷的形式施加于围裙下端面。

表 1 边界条件设置Table 1 Setting of boundary condition

1.6 隐式算法求解

在对上述连接结构精细化模型直接进行静力有限元强度校核时，由于围裙的大变形以及接触的非线性容易出现结构求解不收敛的问题，本文将围裙连接结构承载过程视为准静态问题，采用缓慢加载的方式，利用隐式动态算法进行计算。结构系统通用的运动学方程为[10]：

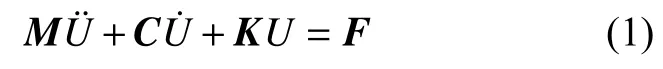
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F为结构载荷；U为节点位移。

本文选择隐式算法中应用性较好的Newmark法进行求解。假设在时间间隔[t，t+ Δt]内节点加速度线性变化，可得到如下速度、加速度公式：

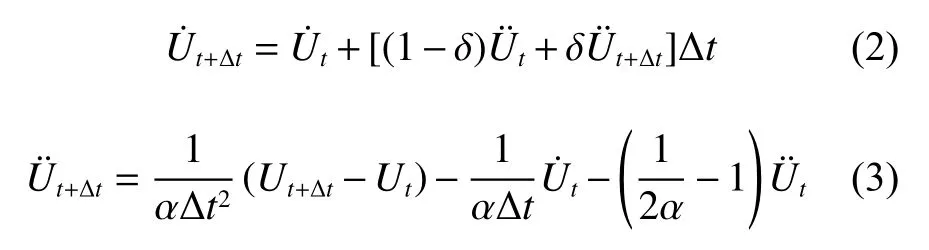
式中， α,δ为控制计算精度与稳定性的可调参数。

将式(2)和式(3)代入式(1)，整理得到

其中：

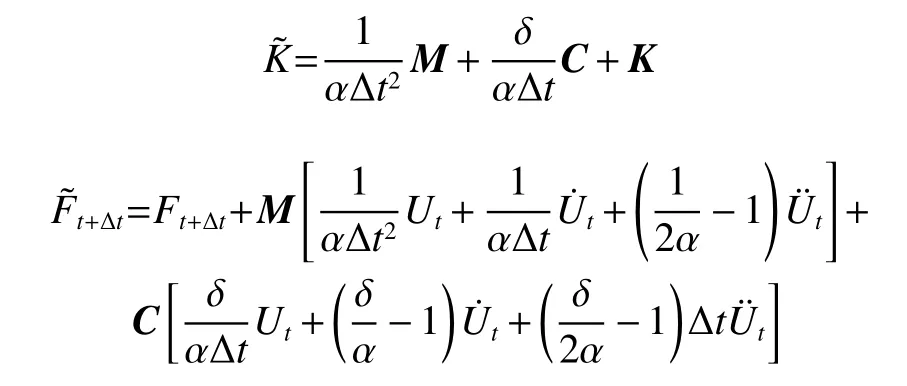
随后，利用Newton-Raphson算法对式(4)进行求解。将结构承受的载荷分为若干个增量，在增量步内迭代获得近似解，一旦近似解偏离平衡位置，便执行下一个迭代，最后，所有增量步的总和就是所求近似解。

2 围裙连接结构的力学特性分析

2.1 工况定义

气垫船正常航行时多处于垫升工况，此时，船舶匀速航行于水面之上，遭遇的海况一般不超过4级。当气垫船遭遇高海况而完全失去气垫压力时，船体在波浪上运行，此时，气垫船处于极端海况，连接结构承受的围裙张力很大。在实际使用过程中，处于垫升工况下的气垫船连接结构仍然有可能出现构件断裂破坏的问题，因此，有必要考虑垫升工况和极端工况下连接结构的应力响应。

施加于连接结构的载荷一般认为是围裙在气压作用下产生的张力，现有的简化分析法[11]假设张力T处处相等，计算公式为：

式中：P为围裙受到的气压；R为 给定剖面内结构的曲率半径。

考虑到艏部围裙为三维结构，因此任一剖面围裙的应变响应都会受到相邻两个剖面的约束。简化计算公式只考虑了剖面内的纵向张力，忽略了剖面外的横向张力影响[12]，而结构的复杂性会造成横向张力无法准确计算，即使将现有计算公式扩展至三维结构，计算精度也不高。本文根据某气垫船围裙系统静垫升时的成型结果，得到静垫升状态下艏裙区域围裙的张力TB=28.6 kN/m[13]。通常情况下，当气垫船在垫升工况和极端工况下运行时，对于作用于围裙上的张力，应在静垫升的基础上分别考虑压力过载系数np=2.0和4.0。具体计算工况如表2所示。

表 2 艏部连接结构的计算工况Table 2 Calculation condition of bow's connection structure

2.2 垫升工况

图3所示为垫升工况下围裙承载后的结构应力云图。从应力分布来看，在垫升工况下，连接结构除局部点接触外，大多数构件远未达到屈服应力，仍处于安全状态。以围裙铰链为例，因承受拉力时围裙在泊松效应的影响下厚度会相应减小[6]，故螺栓结构的预紧作用会减弱。螺栓孔应力从螺栓预紧阶段的147.8 MPa下降到了133.2 MPa，平板区域应力从87.1 MPa下降到了57.2 MPa。图4所示为对应工况下销轴的应力云图。作为围裙连接结构重要的承拉构件之一，在垫升工况下，连接结构的最大应力出现在销扣附近的销轴上，其主要原因是销扣的存在使得销轴局部刚度得到极大提高，所以首个围裙铰链与销轴接触区域应力很大。虽然销轴表面局部区域已达到屈服强度，但是销轴剖面绝大部分区域仍处于安全状态，未完全丧失承载能力，所以发生破坏断裂的概率不高。这由此说明，在垫升工况下，该连接结构从理论上讲不应该发生结构破坏。

图 3 垫升工况下艏部连接结构应力云图Fig.3 Stress contours of bow's connection structure under lifting conditions

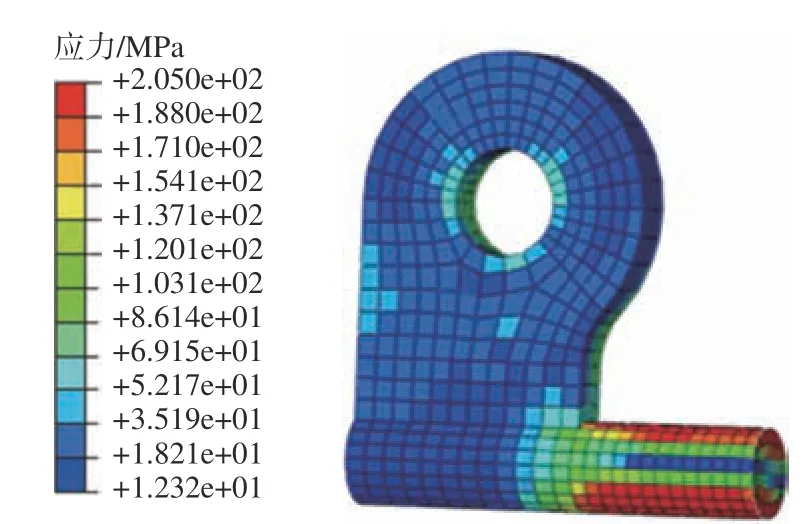
图 4 垫升工况下艏部连接结构的销轴应力云图Fig.4 Stress contours of pin shaft in bow's connection structure under lifting conditions

2.3 极端工况

极端工况与垫升工况的区别在于，围裙承受的载荷大小不同。在极端工况下，连接结构的应力分布与垫升工况基本相同，但由于承受的载荷更大，导致关键构件的应力明显升高。图5 给出了极端工况下船体板与销轴的应力云图。从图中可以看出，在极端工况下，船体板螺栓孔的上缘局部达到了屈服强度，由于船体板一般较薄，此时有较高的概率会发生破坏；销轴端部由于存在销扣结构，使得几乎全部剖面都达到了屈服强度，说明此时销轴的承载能力下降严重，发生断裂的概率很高。

铰链构件同样是实际使用中易发生损坏的构件，本节选择图2中受边界影响最小的第2对铰链组合结果进行讨论。图6和图7分别反映了围裙铰链和艇体铰链在不同工况下的应力分布情况，两者的应力分布基本相同。从计算结果看，铰链下表面的应力高于上表面，所以后续的讨论均考虑更危险的下表面。以围裙铰链为例，在垫升工况下，铰链受螺栓预紧力的影响在螺栓孔附近出现了最大应力，而在过渡区域和搭扣区域则出现了局部的应力集中，且数值相差不大，说明此时过渡区域与搭扣区域是共同承载的。在极端工况下，最大应力出现在过渡区域的左、右两端，其原因主要有两方面：一是由于销轴发生弯曲变形，使得铰链两端与销轴发生接触而率先承载，造成应力集中从左、右端面向中间逐渐扩展；二是从平板区域到过渡区域时铰链宽度逐渐减小，进入搭扣区域后曲率会发生变化，致使应力传递受阻，从而造成过渡区域应力集中。

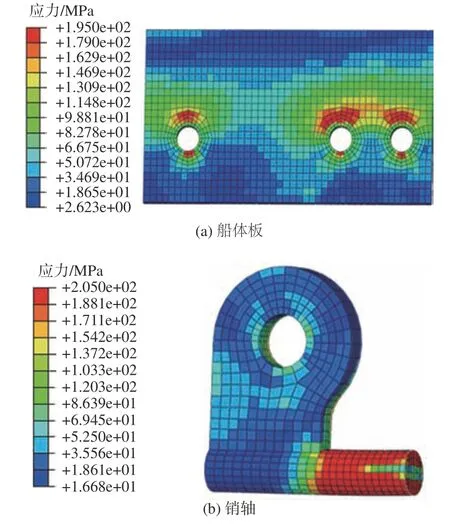
图 5 极端工况下艏部连接结构的构件应力云图Fig.5 Stress contours of components in bow's connection structure under extreme conditions

3 围裙连接结构改进

设计时，一般认为铰链可以自由转动，所以常选用较小的板厚与销轴半径。但从上述仿真模拟和实际使用结果看，船体板、销轴以及铰链等构件极易发生失效破坏，因此有必要对相关构件进行改进。船体板和销轴结构较简单，一般采取增加厚度（半径）或采用高强度材料的方法即可[9]。而现有的铰链形式主要受制作工艺的影响，其结构仍有改进的空间，采取增加板厚或改用材料的方法得到的不一定是最优解。为解决围裙铰链的应力集中问题，提出2类铰链设计改进方案：一是对铰链薄弱区域进行局部加厚；二是将铰链的开放式搭扣改为封闭式。除铰链外模型均不变化，计算工况选择极端工况。

3.1 铰链局部加厚

该类方案不改变铰链的结构，只对过渡区域进行局部加厚，最大厚度达7 mm。根据搭扣与过渡区域加厚的平滑范围，设置了3个子方案，即方案1-a、方案1-b和方案1-c，具体设计如图8所示。3个子方案的应力分布情况基本相同，下面以方案1-a的围裙铰链应力结果为例进行讨论。

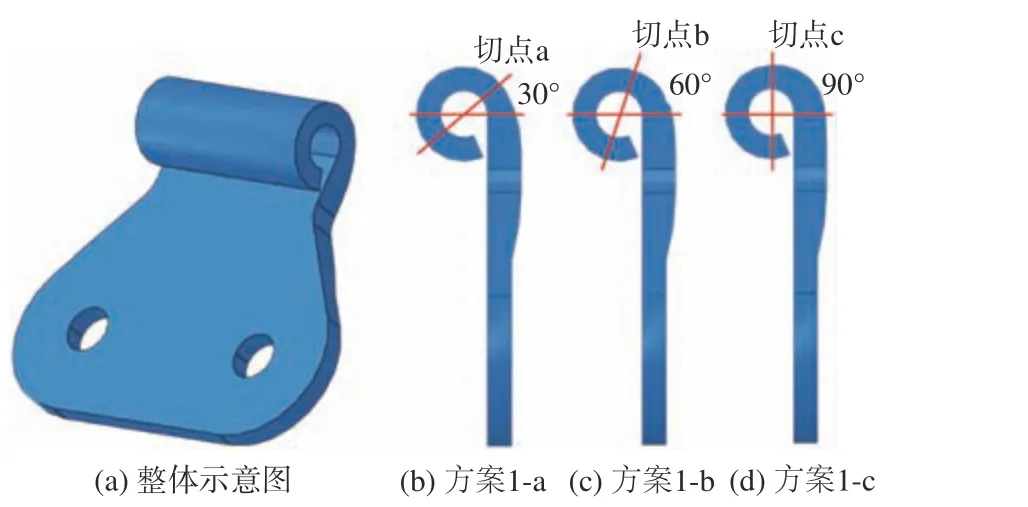
图 8 极端工况下局部加厚围裙铰链方案设计图Fig.8 Design drawing of partially thickened skirt hinge scheme under extreme conditions

从图9所示的围裙铰链下表面应力分布可以看出，改进前出现应力集中区域的最大应力从205.0 MPa下降到了120.0 MPa，降幅达41.5%，但在搭扣与过渡区域加厚的平滑范围，仍出现了应力集中，最大应力仍达205.0 MPa。造成这一现象的原因有2方面：一是该区域受力复杂，同时承受拉伸和剪切作用；二是加厚时需保证不同区域光顺连接，而平滑范围过小会造成厚度变化明显，结构刚度发生较大变化，易出现应力集中。

图 9 极端工况下局部加厚的围裙铰链应力云图(方案1-a)Fig.9 Stress contours of partially thickened skirt hinge under extreme conditions (scheme 1-a)

从图10所示的局部加厚围裙铰链应力结果汇总可以看出，方案1-c的平滑范围最大，使得区域刚度变化减缓，因而有效改善了应力集中问题，最大平均应力与改进前相比下降了24.3%；3种方案在最小平均应力方面的表现基本相同，均下降约50%。对铰链采用局部加厚设计时，应尽可能保证充足的平滑范围，以防止局部加厚带来的构件应力集中问题。

3.2 铰链封闭搭扣

该类方案不改变铰链的厚度，将搭扣端部与过渡区域进行连接，然后根据连接形成的不同角度分别设置3种子方案，即方案2-a、方案2-b和方案2-c，具体设计如图11所示。3个子方案的应力分布情况基本相同，下面以方案2-a的围裙铰链应力结果为例进行讨论。

图 10 极端工况下局部加厚围裙铰链方案应力结果汇总Fig.10 Summary of stress results of partially thickened skirt hinge scheme under extreme conditions

图 11 极端工况下封闭转圆围裙铰链方案设计图Fig.11 Design drawing of closed-round skirt hinge scheme under extreme conditions

从图12所示的围裙铰链下表面应力分布可以看出，除局部接触外，搭扣区域左、右两端最大应力下降明显，从205.0 MPa下降到了116.2 MPa，降幅达43.3%，相比局部加厚方案，本方案构件的应力分布更加均匀；改进后的铰链最大应力出现在搭扣端部附近，只有199.3 MPa，构件大部分区域的应力在130.0 MPa以下，而改进前过渡区域的最大应力为205.0 MPa，高应力区域范围较大，大部分区域的应力在140.0 MPa以上。封闭搭扣设计将搭扣的自由端与较薄弱过渡区域刚性连接，使得搭扣部分与过渡区域形成结构刚度与强度更大的闭式结构，从而大大提高了围裙铰链的承载能力。

图 12 极端工况下封闭转圆围裙铰链应力云图（方案2-a）Fig.12 Stress contours of closed-round skirt hinge under extreme conditions (scheme 2-a)

根据图13所示的封闭搭扣围裙铰链应力结果汇总可以看出，3种子方案均可有效改善铰链的应力分布情况，效果相差无几，最大与最小平均应力分别下降了20.1%和16.9%。其主要原因在于，受构件过渡区域尺寸的限制，可操作的连接角度有限，因而导致结构刚度变化不明显。所以在使用封闭搭扣形式设计铰链时，搭扣端部与过渡区域的连接角度几乎不影响构件的承载能力，可以根据工艺要求合理选择。

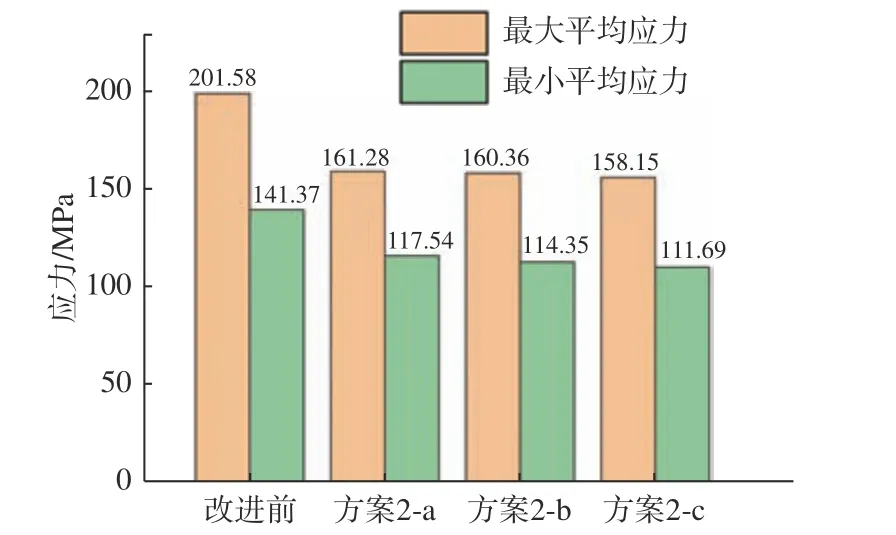
图 13 极端工况下封闭转圆围裙铰链方案应力结果汇总Fig.13 Summary of stress results of closed-round skirt hinge scheme under extreme conditions

4 结 论

本文在考虑螺栓预紧力、结构大变形以及构件相互接触等因素的基础上，构建了艏部围裙连接结构的三维精细化模型，利用整船围裙系统的成型有限元结果，获得了不同工况下的围裙载荷，研究了垫升工况和极端工况下围裙连接结构的力学特性，并针对关键构件提出了设计改进方案，得到以下主要结论：

1） 所采用的数值仿真方法能够较为真实地考虑螺栓预紧作用，对围裙承载下构件的精细化模型计算分析较容易得到其应力水平和分布情况，从而有效确定连接件局部损坏的原因。

2） 垫升工况下，围裙连接件绝大多数构件的应力水平处于合理范围，仅销轴端部出现了小范围的高应力；但在极端工况下，船体板、销轴端部以及铰链过渡区域这3处的应力水平明显过大，设计时应对这些区域进行加强。

3） 局部加厚与封闭搭扣设计均能有效提高铰链的承载能力，其中采用局部加厚设计易出现应力集中问题，故需保证充足的平滑范围；采用封闭搭扣设计时，可以根据工艺的需要选择合适的连接角度。其中，封闭搭扣设计可以使应力分布更均衡，是相对较优的设计方案。