一道椭圆试题的教学探究及其启示*
江苏省姜堰第二中学 (225500) 史记祥 朱传美
圆锥曲线的魅力经久不衰,历史上众多数学些结论家为之痴迷、陶醉.笔者在讲授此章节时,时常就某些结论引导学生进行一些引申、探究,得到了一些有价值的结论.通过这样的探究过程,很好地培养了学生的学习兴趣和探索精神,有效地提升了学生的数学核心素养.
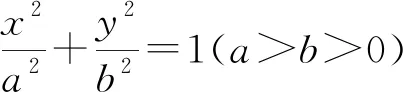
师:这是在众多高三复习资料中常见的一道经典的试题,其证明方法并不复杂.我们感兴趣的并不在于本题的解法,而在于本题的引申及探究.
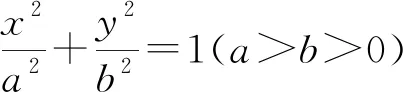
师:哪位同学来证明一下?(老师抛砖引玉,先给出引申1)
教室里安静片刻后.
生1(板书):

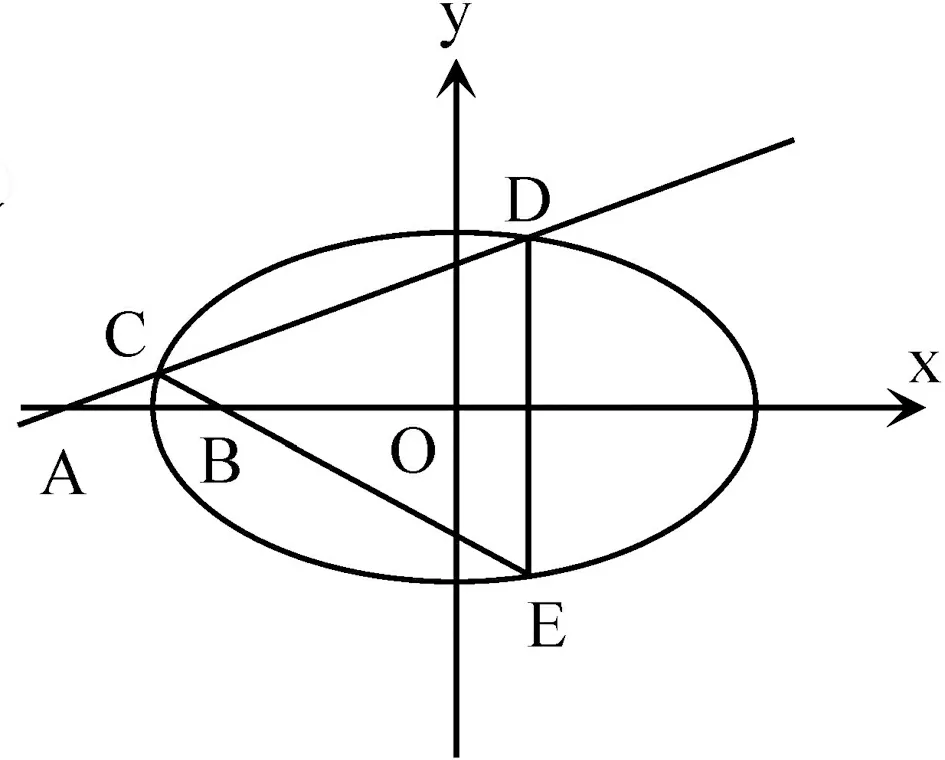
图1
师:很好!我们这里把短轴两端点拓展为关于x轴对称的两点,原有结论仍然成立.那引申能否继续?(老师很自然地把问题抛给学生)
众生积极思考,跃跃欲试.
生2(板书):
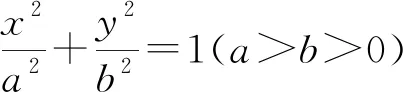
生3(板书):
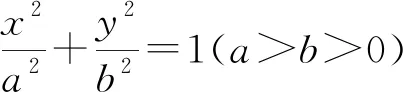
生4:证明呢?
生2、生3(害羞):我们只是猜想,还没证出来.
师:根据我们以往的经验,这两个命题应该都是真命题,但课堂上时间有限,留给大家课后完成.
师(补充相关知识):人们常称x轴上的横坐标乘积为定值a2的两个点为一对“伴侣点”,因为它们总是成对出现,而且相处的很和谐.
众生:哦!原来如此.
至此,学生的探究热情已被老师高高地燃起,都在积极思考着.
生5(板书):
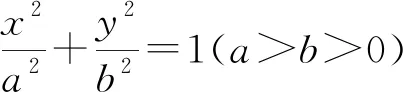

图2
生5:A、B就是椭圆在x轴上的一对“伴侣点”.此命题也提供了“伴侣点”的一种作法.
生5(板书):
证明:如图2,设D(m1,n1)、E(m1,-n1)、F(m2,n2)、C(m2,-n2) (|m1|≠|m2|),则易得A、B两点都在x轴上且横坐标分别为
师:生5利用椭圆的对称性把原有图形补充为椭圆的一个内接等腰梯形,从而发现了“伴侣点”的一种作法,看来探究很有收获.
探究仍在继续,众生忙碌,老师巡视!
生6(板书):
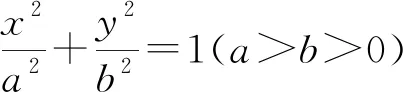
师:看着应该是个真命题,下面就来证证看.
可此命题的证明难度很大,一时间,教室里炸开了锅,讨论很是热烈,因为老师也不知怎么证,就时不时地加入到各个讨论群,但转眼十多分钟过去了,还是没有成功.
师:这个命题的证明确实很难,就留待我们课后继续探讨,下面请大家再想想,能否再给出更多引申.
生7(板书):
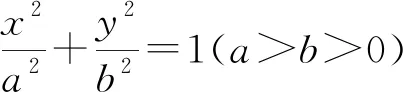
生7:A、B就是椭圆在y轴上的一对“伴侣点”.
师:很好.能证明吗?
仿前面的证明,众生很快就解决了!
师:厉害,这么快就学会模仿了.
众生大笑.
生8:那么在平行于坐标轴的直线上也有“伴侣点”吗?我正在找,可还没找着.
师:好,下面我们就一起来帮他找.
在师生的共同努力下,很快又得到如下引申.
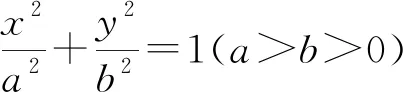
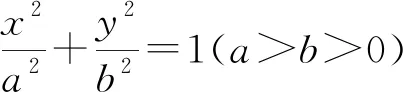
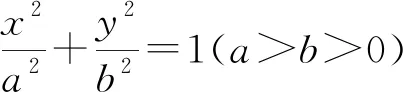
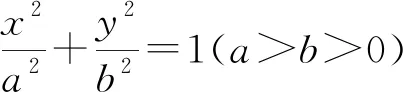
下课铃已经响了,但探究还在继续……
第二天上课时,笔者还了解到:学生早已解决了引申2、引申3及引申5的证明,并且还把相关结论向双曲线及抛物线做了推广,笔者惊喜地发现学生学习椭圆的积极性大涨,当然,第二天的数学课堂气氛很好,效率也非常高.
结束语
新课标强调要凸显学生的主体地位,让学生勇于探索,亲身感受或经历数学知识的发生历程,而我们的教师往往顾忌教学效果,拘泥于教学计划,而不敢放开手让学生自发地提出问题,共同解决问题.传统的教学中教师的认真教,学生的照着学,充其量只能是一种模仿,其实,教师可以不把现成的结论和方法直接告诉学生,而应让学生自己对学习的对象进行探索、研究,自己去获得.课堂上,教师只能是组织者、指导者和参与者,教师只能起到主导、指导、向导和路标的作用;学生才是主体,是学习研究的探索者、创新者和实践者,而教师的作用就是在教学过程中要为学生营造一个宽松、和谐、积极、民主的学习环境,使每位学生都能成为问题的探索者、研究者和发展者.
数学核心素养的提升可以落实到数学教学的方方面面,老师要做学生数学核心素养提升的指导者,引路人,积极创造研究氛围浓厚的数学课堂教学,激发学生内在数学核心素养提升的强烈欲望,促成学生数学核心素养的快速提升.

