2020年广东中考“圆的综合题”的解析与思考

广东省东莞市竹溪中学(523960) 余再超

广东省江门市蓬江区荷塘中学(529095) 华本秀

2020年,广东省数学中考改革,时间上减少10 分钟,题量不变,以前该题型作为中考试卷第24 题压轴题出现,总分9 分.2020年广东中考数学卷圆的综合题在第22 题,总分8分,设问两问,难度有所降低.笔者有幸参加今年的中考评卷,发现,1000 人中,有692 人只得1 分以下,仅有49 人6 分以上,根据本次评卷的情况,本文对该题进行知识点分析及解法技能剖析,在培养和发展学生数学抽象、逻辑推理、数学建模等数学素养的问题上做了归类和思考.

1 题目呈现

(2020年广东省中考第22 题)已知: 如题22 图,在四边形ABCD中,AD//BC,∠DAB= 90°,AB是⊙O的直径,CO平分∠BCD.

(1)求证: 直线CD与⊙O相切;

(2)如题22-2 图,记(1)中的切点为E,P为优弧AE上一点,AD=1,BC=2,求tan ∠APE的值.

图1

图2

【考点】切线的判定、切线长定理、圆的基本性质、圆周角定理、相似三角形、三角函数、勾股定理、射影定理、全等三角形判定及性质定理、平行线的性质.

【解析】无切点作垂直证半径,切线长定理,直角三角形的判定,相似三角形的运用、辅助线的作法(应用创新意识).

2 解法分析

本题考察的知识点有切线的判定和正切函数的求解,解答本题可能运用到的知识点有: 平行线的性质、角平分线性质、全等的判定、勾股定理、切线长性质、同弧所对的圆周角和圆心角的关系、相似三角形的判定、相似三角形性质的运用、直角三角形的判定、射影定理等.所用到的思想方法是:添加辅助线(应用创新意识)、数形结合思想、转化相等角和化归思想、数学抽象并建模直角三角形的数学建模思想.

2.1 用数学的眼光观察世界——发展学生数学抽象素养

本题第一问考察的是切线的判定,在初中教学中,切线的判定方法主要有两种: ①过半径的外端点且垂直于半径的直线是圆的切线; ②到圆心距离等于半径的直线是圆的切线.简单的证明步骤抽象为: ①知切点, 连半径, 证垂直.②无切点,作垂直,证半径.本题第一层面考核学生数学抽象和直观想象的核心素养.即题目中没有出现切点,却出现了角平分线,因此,思考的方向为: 无切点,作垂直,证半径.

具体解题方法为以下两种:

2.1.1 方法一: 利用角平分线上的点到两边的距离相等推出OB =OE

证明: 如图3,过点O作OE ⊥CD交于点E.∵AD//BC, ∠DAB= 90°,∴∠OBC=90°,即OB ⊥BC.∵OE ⊥CD,OB ⊥ BC,CO平分∠BCD,∴OB=OE.∵AB是⊙O的直径,∴OE是⊙O的半径.∴直线CD与⊙O相切.

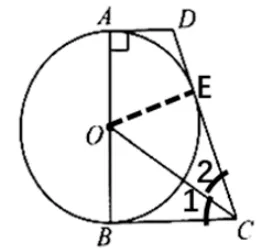
图3

2.1.2 方法二: 利用ΔOBC ∽= ΔOEC 推出OB =OE

证明: 如图3, 过点O作OE ⊥ CD交于点E.∵AD//BC, ∠DAB= 90°, ∴∠OBC= 90°.∵CO平分∠BCD,∴∠1 = ∠2.∵OC=OC,∠OBC= ∠OEC= 90,∴ΔOBC∽= ΔOEC.∴OB=OE.∵AB是⊙O的直径,∴OE是⊙O的半径.∴CD是⊙O的切线.

2.2 用数学的思维分析世界——发展学生逻辑推理素养

本题考察的第二问是要求解∠P的正切函数,通常是要构建直角三角形,找到含有∠P的直角三角形,或者,观察转化∠P对应相等的其它角的函数值.本题第二层面考核学生的逻辑推理和数学运算的核心素养.题目中∠P并非在直角三角形中,因此,思考方向有两种: ①构造一个以∠P为其中一个锐角的直角三角形.②通过角的转换,把∠P转化为其它直角三角形里面的锐角.由于∠P是圆的一个圆周角,根据圆周角的性质,本题选择对∠P进行转换.转换∠P解法如下,并利用RtΔAOD,推出

证明: 如图4,∵直线AD,DC,BC都是⊙O的切线, ∴∠1 = ∠2,∠3 =∠4,∠5 = ∠6.DE=AD= 1,CE=BC= 2,DC= 3.= ∠4 =∴∠P= ∠3 = ∠4.∵∠5 = ∠6,∠3 = ∠4,∠3+∠5 + ∠4 + ∠6 = 180°, ∴∠3 + ∠5 = 90°.∵∠1 + ∠5 =90°,∠3+∠5 = 90°,∴∠3 = ∠1.∴∠P= ∠3 = ∠4 = ∠1 =∠2.∵OE ⊥DC,∠ODE= ∠CDO, ∴ΔODE∽ΔCDO.∴在RtΔAOD中,

图4

2.3 用数学的语言表达世界——发展学生数学建模素养

本题考察的第二问要求解∠P的正切函数值,需要直角三角形的直角边长的比值.通过2.2 以上的解法,我们发现,每一个与∠P相等的对应角所在的直角三角形中,需要用到圆的半径.本题第三层面考核学生的数学建模和数据分析的核心素养.因此,我们继续思考方向就是解决半径长度.由于圆经常和相似三角形合作,因此,不难想到通过相似三角形对应边成比例及勾股定理来求解半径长度.

2.3.1 方法一: 利用在RtΔAOD、RtΔBOC、RtΔOCD中分别用勾股定理,求得r =

【思路分析1】 如图5, 在RtΔAOD, RtΔBOC,RtΔOCD中分别用勾股定理得:AD2+r2=OD2,BC2+r2=OC2,OD2+OC2=CD2,由此求得进而求得具体解法如下:

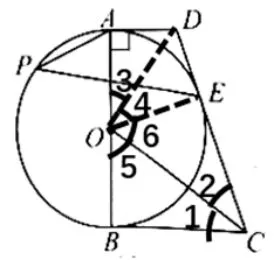
图5

证法1: 如图5, ∵在RtΔAOD中,AD2+r2=OD2,在RtΔBOC中，BC2+r2=OC2,在RTΔOCD中,OD2+OC2=CD2,∴AD2+r2+BC2+r2=CD2.∵AD= 1,BC= 2,DC= 3, ∴12+r2+ 22+r2= 32.∴r=∴tan ∠P=tan ∠3=

2.3.2 方法二: 利用ΔOAD ∽ΔCBO,或者ΔODE ∽ΔCOE,得出:,求得: r =

【思路分析2】 如图6, 通过证明ΔOAD∽ΔCBO,或者ΔODE∽ΔOEC, 进而写出关于半径的比例式子:由此求得r=进而求得tan ∠P=

图6

证法2: 如图6, ∵∠OAD= ∠B= 90°, ∠3 = ∠1,∴ΔOAD∽ΔCBO.∴.∵AD= 1,BC= 2,OA=OB=r, ∴∴tan ∠P= tan ∠3 =

2.3.3 方法三: 利用构建新的RtΔFCD 和矩形ADFB用勾股定理,求得: r =

【思路分析3】 如图7, 作DF⊥BC于F, 得矩形ADFB,在RtΔFCD中分别用勾股定理得:FD2+FC2=CD2,由此求得r=进而求得tan ∠P=

证法3: 如图7, 过D作DF⊥BC于点F.∴四边形ADFB是矩形.∴BF=AD=1,FC=BC −BF=1.∵在RTΔFCD中:FD2+FC2=CD2,FC=1,DC=3,∴FD2+12= 32.∴FD=∵AB=DF, ∴r=∴tan ∠P=tan ∠3=

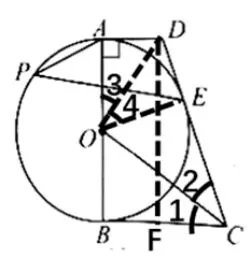
图7

2.3.4 方法四: 利用构建新的RtΔABF 使得ΔADE ∽ΔFCE,推出,求得:

【思路分析4】如图8,延长AE交BC延长线于点F,则ΔADE∽ΔFCE,因此:,EF= 2AE,再由射影定理得:BE2=AE×EF=2AE2,,进而求得: tan ∠P=

图8

证法4: 延长AE交BE延长线于F.∵AD//BC,∴ΔADE∽ ΔFCE.∵DE= 1,CE= 2,∴EF= 2AE.∵在RTΔFBA中,AF⊥BE,∴BE2=AE × EF= 2AE2.∴tan ∠P=tan ∠ABE=

3 考情分析

抽样发现，本题分值8 分,平均分1.49 分,学生完成本题目答卷情况如上,明显成绩非常低,样本为1000 人仅有49 人6 分以上.

表1 各个得分值比例分布

究竟是什么原因导致这样呢? 通过卷面分析发现:

(1)学生的概念不清晰,在阐述OC是∠BCD的角平分线之后,学生在得到∠2 = ∠1 的结论,就直接说BC=EC,这是角平分线的概念不清晰.比较多考生一开始便直接“连结OE”(虽然E点在第一问在条件中根本没有出现),然后把OE=OB作为已知条件证明全等从而得出∠OEC= 90°.这是切线的概念以及全等的概念不清晰,学生逻辑推理核心素养欠缺.

(2)思维定势限制了学生的思考,构建解题模型思维,或是,构建数学模型能力薄弱,创新应用意识淡薄等,制约学生的思考.在初中教学中,切线的判定方法主要有: ①过半径的外端点且垂直于半径的直线是圆的切线; ②到圆心距离等于半径的直线是圆的切线.其中在平时的练习中①比②更常见,使用率更高,因此大部分考生认为证切线就是证垂直,而没有考虑要证明的直线是否和圆有已知的交点.更是忽略了第二种情况.

(3)学生的综合能力不强,空间想象和运算求解能力欠缺,导致学生计算出错无法得分.不少考生证明到相似的比例式:,却无法解出正确的r=

(4)学生的思维品质较低,对问题深刻性理解不够,第(2)问涉及的考点比较多,很多考生完全没有思路,直接放弃.其实这道题需要用到常用的数形结合思想和转化化归思想,图中很容易看出相似三角形,而且有多对相似三角形,只要能找出相似三角形就容易通过比例求出半径,或通过设未知数用勾股求出半径,方法非常多,而且∠P是圆周角,圆周角的转换也是平时练得较多的内容,但学生就是不愿意去想,不愿意去尝试.

4 教学思考

怎样才能在课堂上更好的发展学生数学抽象、逻辑推理、数学运算、数学建模等核心素养呢? 怎样才能提升学生的数学品质和情感态度及能力呢?

(1)授课时概念要理解清晰,要注重学生对所学知识的理解,体会数学知识之间的关联.学生掌握数学知识,以理解为基础,并在知识的应用中不断巩固和深化.因此,在教学中,要把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解.

(2)授课时要注重变式训练,变式训练的目的是使学生在练习过程中把握题目的本质特征,达到“以不变应万变”,彻底打破学生的定势思维.通过针对性的变式训练让学生了解每一种变式都有它的特定目的,从而激发学生的练习兴趣,使他们自觉地产生完成练习的内动力,提高练习效率.在教学过程中的变式训练要有合适的梯度,逐步增加技巧性因素,在变式的过程中掌握、保持和巩固数学技能,从而提高学生的解题能力.

(3)授课时要注重数学思想的培养.数学思想蕴涵在数学知识的形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括.如数形结合思想、分类讨论思想,转化与化归思想等.