理解基本图形关系 提升几何推理能力

文 董荣玉

四边形既可以以平行四边形、矩形、菱形、正方形出现，也可以用普通身份出现；试题中，既可以考查四边形的知识点，也可以包罗三角形等其他知识点，而这其中少不了与圆的结合。下面，老师就结合一些中考题与同学们共同感受一下四边形与圆的完美呈现。

一、开门见山，直截了当

例1（2020·浙江湖州）如图1，已知四边形ABCD内接于⊙O，∠ABC=70°，则∠ADC的度数是（ ）。

图1

A.70° B.110° C.130° D.140°

【解析】直接运用四边形内接于圆的性质：圆内接四边形的对角互补。所以∠ADC=180°-∠ABC=180°-70°=110°。故选B。

【点评】本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键。

例2（2020·山东滨州）如图2，⊙O是正方形ABCD的内切圆，切点分别为E、F、G、H，ED与⊙O相交于点M，则sin∠MFG的值为_____。

图2

【解析】连接EG，如图3。因为⊙O是正方形ABCD的内切圆，所以，EG=BC。根据圆周角的性质可得∠MFG=∠MEG，所以。故答案为。

图3

【点评】本题是以正方形内切圆为背景，通过利用切线性质和切线长定理得到角和线段的关系。求三角函数值需将此角放置于直角三角形中，而直角也是由切线得到的。

二、半遮半掩，引人入胜

例3（2019·江苏盐城）如图4，点A、B、C、D、E在⊙O上，且为50°，则∠E+∠C=______°。

图4

【解析】连接EA，如图5，构造四边形DCAE为⊙O的内接四边形。根据圆的内接四边形对角互补得到∠DEA+∠C=180°，结合为50°，得到∠BEA=25°，所以∠DEB+∠C=180°-25°=155°。故答案为155。

图5

【点评】本题考查的是圆内接四边形的性质、圆周角定理。作辅助线构造出圆内接四边形，掌握圆内接四边形的对角互补是解题的关键。

三、深藏不露，魅力无穷

例4（2019·山东德州）如图6，点O为线段BC的中点，点A、C、D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是（ ）。

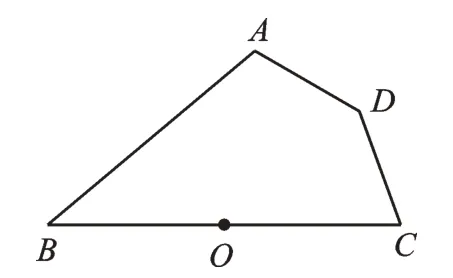
图6

A.130° B.140° C.150° D.160°

【解析】由点O为线段BC的中点，点A、C、D到点O的距离相等可得到OA=OB=OC=OD。根据圆的定义（到定点的距离等于定长的点的集合），可知点A、B、C、D在以点O为圆心的同一个圆上，所以作出圆O，如图7。因此，四边形ABCD为⊙O的内接四边形，∠ABC+∠ADC=180°，所以∠ADC=180°-∠ABC=140°。故选B。

图7

【点评】本题表面上是四边形的图形，如果直接求解会比较麻烦。当题目中出现到同一点的距离相等时，我们可以巧妙借助隐藏的辅助圆，再根据圆内接四边形的性质就可以轻松解决。

四、拓展外延，精彩提升

例5（2019·江苏南京）如图8，PA、PB是⊙O的切线，A、B为切点，点C、D在⊙O上。若∠P=102°，则∠A+∠C=________。

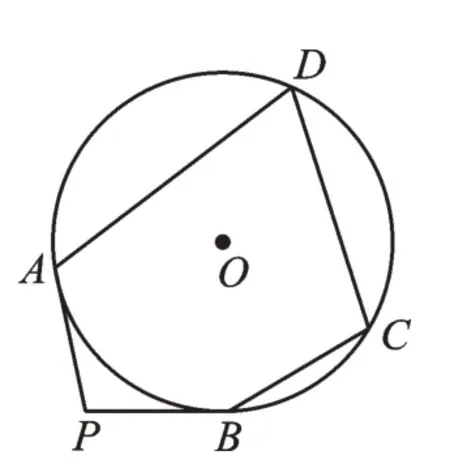
图8

【解析】本题是五边形和圆的结合，没有直接联系的知识点，所以要构造有关联的图形。连接AB，如图9，因为PA、PB是⊙O的切线，根据切线长定理（过圆外一点所画的圆的两条切线长相等），得PA=PB；再根据等腰三角形性质，由∠P=102°，得（180°-102°）=39°；根据圆的内接四边形对角互补，得∠DAB+∠C=180°，所以∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°。故答案为219°。

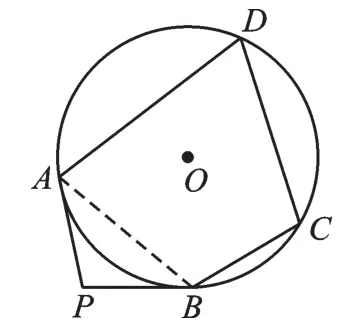
图9

【点评】本题将五边形分割成四边形和三角形，从而可以利用切线长定理、圆内接四边形的性质、等腰三角形的性质来解决问题。正确作出辅助线，把多边形转化为圆内接四边形，掌握切线长定理是解题的关键。