Hilbert空间中一类新的随机集值隐拟变分不等式

周 武，宋建成

(西南民族大学数学学院，610041)

众所周知，变分不等式问题是一类丰富的决策问题，和不动点问题、相补问题和优化理论紧密相关.可以用于解决大量产生与力学与热学、决策与管理、交通与运输、运筹与优化等领域的现实问题.拟变分不等式是变分不等式的重要推广，其约束集是具有非空闭凸值的集值映射.近年来，国内外不少学者对变分不等式和拟变分不等式及其相关问题的理论、算法及其应用进行的系统研究，获得了许多重要结果，参见[1-5]及其参考文献

由于现实问题往往会受随机干扰，因此，如何在随机环境下研究变分不等式和拟变分不等式是一项重要工作.早在1986年，Tan[6]在局部凸Hausdorff拓扑向量空间中引入并研究了一类随机拟变分不等式，利用Fan极大极小不等式定理和可测选择定理，得到了该类随机拟变分不等式问题解的存在性结果.1989年，张和朱[7]研究了一类随机变分不等式和随机拟变分不等式问题解的存在性结果.1994年，黄[8]引入并研究了一类随机广义集值强非线性拟变分不等式问题，并构造了逼近问题解的迭代算法，获得了这类随机广义集值强非线性拟变分不等式问题解的存在性以及算法所产生的随机迭代序列的收敛性.1999年，黄[9]在Hilbert空间中研究了一类涉及随机模糊映射的广义随机变分包含问题，构造了逼近问题的解的迭代算法，证明了该问题解的存在性以及算法的收敛性.最近Ravat和Shanbhag[10]引入并研究了一类随机拟变分不等式和随机相补问题，获得了这些随机问题的可解性结果，并给出了对非光滑广义Nash-Cournot博弈问题及电力市场的应用.其他工作参见[11-16].

受前人工作的启发，本文主要研究可分Hilbert空间中的一类随机集值隐拟变分不等式的可解性问题，利用投影算子技巧、Nadler不动点定理以及不动点的随机化原理，给出了该类随机集值隐拟变分不等式解的存在性结果.本文所得结果，丰富了随机环境下随机变分不等式问题的可解性结果，包含的前人已有结果为特例.

1 预备知识

以下处处假设定(Ω，ℑ，P)是一概率空间，H是一实的可分Hilbert空间(H，B)是一可测空间，其中B是H的一切Borel子集的σ-代数.我们分别用＜，.，＞和‖·‖表示Hilbert 空间H上的内积和范数.进一步地，分别用2H以及C B(H)表示H的非空子集全体以及非空有界闭集之全体.定义C B(H)上的Hausdorff度量为

定义1称一个

①单值映射x：Ω→H为ℑ-可测的(简称为可测)，如果对任意的B∈ℑ，有

②单值映射U：Ω→2H为()-可测的(简称为可测)，如果对任意的B∈ℑ，有

③单值映射u：Ω→H为集值可测映射U：Ω→2H的可测选择，如果u是可测的，且

u(ω)∈U(ω)，∀ω∈Ω.

定义2称一个单值映射

①单值映射T：H×Ω→H为随机算子，如果对于任意给定的x∈H，T(x，ω)＝y(ω)是可测的；

②单值映射T：H×Ω→H为连续的，如果对于任意给定的ω∈Ω，T(·，ω)是H→H的连续映射.

③集值映射U：H×Ω→2H为随机集值映射，如果对于任意给定的x∈H，U(x，·)：Ω→2H是集值可测映射.

④集值映射U：H×Ω→C B(H)为连续的，如果对于任意给定的ω∈Ω，U(·，ω)：H→C B(H)是按照C B(H)上的Hausdorff度量是连续的.

本文以下处处假设F，g：H×Ω→H为随机算子，S：H×Ω→2H以及U：H×Ω→C B(H)为随机集值映射，使得对于任意的x∈H，S(x)是H的非空闭凸子集.

本文考虑如下的随机集值隐拟变分不等问题：寻找可测映射x*，u*：Ω→H对于任意的ω∈Ω有：

随机集值隐拟缤纷不等式问题(1)包括了以下问题作为特例.

(I)若U为恒等映射，则问题(1)将退化为下述随机隐拟变分不等式问题：寻找射x*：Ω→H对于任意的ω∈Ω有：

问题(2)可以看成是文献[11]中所考虑的逆拟变分不等式问题的随机化，可用求随机化环境下的交通流量控制问题.

(II)如果对于任意的x和ω∈Ω，S(x*(ω)，ω)≡S，其中S为H中的非空闭凸子集，则问题(1)和(2)分别退化为下述随机集值隐变分不等式问题：寻找x*，u*：Ω→H对于任意的ω∈Ω，有：

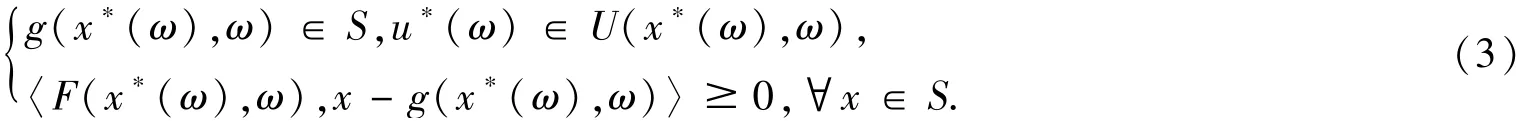
以及随机隐变分不等式问题：寻找可测映射x*：Ω→H对于任意的ω∈Ω有：

(III)若g为恒等映射，则问题(1)退化为下述随机集值拟变分不等式问题：寻找可测映射x*：Ω→H对于任意的ω∈Ω有：

问题(5)可以看成是Chen和Pang[12]中所考虑的广义拟变分不等式问题的随机化，可用求解随机环境下的广义Nash均衡问题.

(IV)如果问题(1)-(5)中对应的约束集为锥，则问题(1)-(5)分别退化为随机集值隐拟相补问题、随机隐拟相补问题、随机集值隐拟相补问题、随机隐相补问题和随机集值相补问题.

为了讨论随机集值隐拟变分不等式问题(1)的可解性，我们需要下述定义与引理.

定义3设S⊂H为非空闭凸集，x∈H到S上的投影算子定义为

引理1[5]设S⊂H为非空闭凸集，z∈H为给定点.则u∈S满足u＝P S(z)当且仅当

引理2[5]投影算子P S是非扩张的，即：

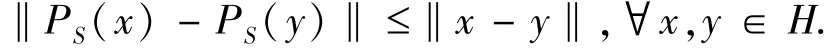
类似于Chan和Pang的[12]的思想，在以下的讨论中，假设随机集值隐拟变分不等式系统问题(1)中约束集S有如下形式：

其中S⊂H中是非空闭凸集，m：H×Ω→H是随机算子.

由引理1以及投影的刻画结果，我们可以得到下述引理.

引理3可测映射x*，u*：Ω→H是随机集值隐拟变分不等式系统问题(1)的解当且仅当，对任意的ω∈Ω，

其中ρ：Ω→(0，∞)为可测函数.

2 主要结果

在本节中，我们将给出本文的主要结果，即随机集值隐拟变分不等式问题(1)解的存在性定理.

定理1假设下述条件成立：

(1)存在可测函数α，γ，ξ：Ω→(0，∞)使得

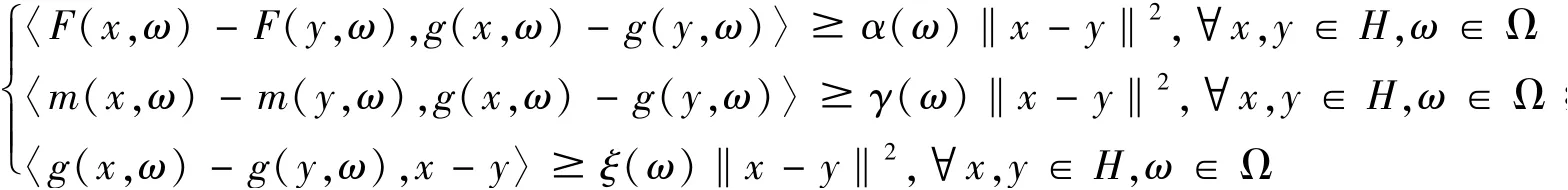
(ii)存在可测函数β，δ，η，λ：Ω→(0，∞)使得

如果存在可测函数ρ：Ω→(0，∞)满足

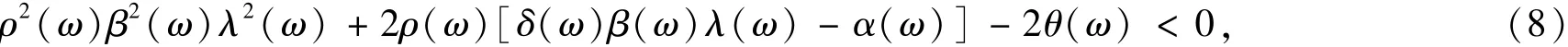
其中，

则存在可测映射x*，u*：Ω→H是随机集值隐拟变分不等式问题(1)的解.

证明：对于任意的(x，ω)∈H×Ω，令

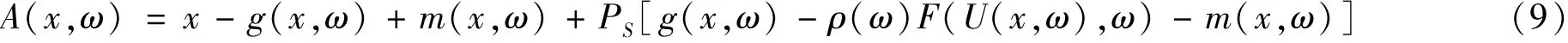
则由定理的条件假设易知A：H×Ω→C B(H)，对于任意给定的x，y∈H以及给定的ω∈Ω，任意选取a∈A(x，ω)，则由(9)可知存在u∈U(x，ω)，使得

因为U(x)，U(y)∈C B(H)，对任意的ε＞0，由Hausdorff度量的定义，我们可以选取v∈U(y，ω)，使得

令

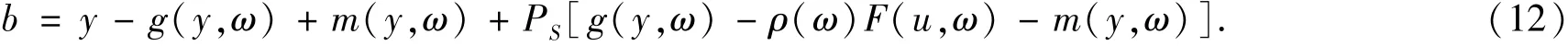
根据投影算子的非扩张性(引理2)以及(10)和(12)，我们有

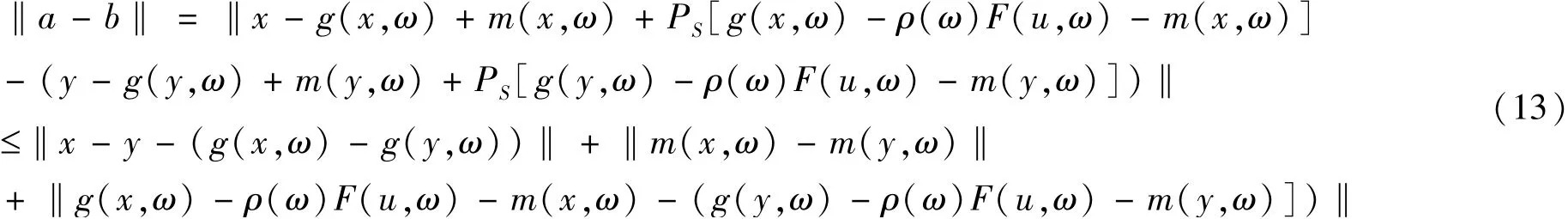
由定理的假设条件及(11)，我们可得

其中

这样，由定理假设条件及(13)和(14)可得

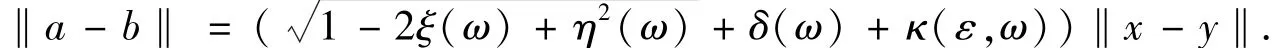
因此，我们有

类似地，我们可以证明

这样，我们有

由ε的任意性，我们得到

因此，由(15)可知，A是一个集值压缩映射，根据Nadler不动点定理[16]，存在x"(ω)∈H使得x"(ω)∈A(x"(ω)，ω)，由于A是Hausdorff连续的，根据随机化原理(文献[6]中定理2.1的特例)，存在可测映射x*：Ω→H满足x*(ω)∈A(x*(ω)，ω).这样，结合引理3可知，存在可测选择u*(ω)∈U(u*(ω)，ω)使得x*，u*是随机集值隐拟变分不等式问题(1)的解.定理1证毕.

注1定理1统一和发展了关于随机拟变分不等式以及随机拟相补问题一些文献中已有的存在性结果.特别地，定理1非常特殊的情形可以看作是Chan和Pang[12]中定理3.5的一个随机集值化推广.另外.与涉及随机集值拟变分不等式的其他结果相比较，定理1的假设条件和证明方法也不一样.