优化算法的量子动力学探讨

王 鹏，陈雅琴，辛 罡，焦育威，尹鑫钰，杨国松，周 岩，穆 磊，王 方

(西南民族大学计算机科学与工程学院，四川 成都610041)

优化算法已经历了半个多世纪的发展，大概可以分为三个阶段(如图1)：第一个阶段是以遗传算法[1]、模拟退火算法[2]、蚁群算法[3]和粒子群算法[4]等经典算法为代表的经典时期，这一时期奠定了后来优化算法的基本格局；第二个阶段是优化算法的繁盛时期，这一时期的特征为大量的新算法、改进算法和混合算法被提出来，优化算法的性能获得了较大的提升.这一时期出现了新算法过多、过滥的问题，新算法的名称千奇百怪，其中以生物名称居多，优化算法的名字几乎可以组成一本生物百科全书；第三个阶段是优化算法的统一阶段，这一阶段大家发现优化算法可能存在核心迭代过程，一些算法被简化后的骨架算法被提出来进行研究，这些骨架算法出人意料的具有不错的性能[5-7].但长期以来优化算法都缺乏严格完备的数学基础，这一问题阻碍了优化算法成为一门严肃的科学，需要寻找一个具有完备数学框架的模型来对优化算法进行描述.

寻找优化算法的数学模型，量子力学是一个重要的备选理论.著名物理学家费曼认为“自然不是经典的，如果你想模拟自然，你最好把它变成量子力学”.量子力学所描述的概率化的世界图像与优化算法迭代过程中的概率行为具有内在的相似性.从二十世纪九十年代开始，量子理论中的量子比特、叠加态原理、退火原理就被大量的用在对优化算法的改进研究中，出现了一大批如量子遗传算法[8]、量子粒子群算法[9]、量子退火算法[10]等量子混合算法.世界上第一台实现了商业化的量子计算机D-Wave系统其实是一台用于解决优化问题的专业计算机，D-Wave在解决优化问题上的成功，证明了优化问题是一个可以被量子理论有效描述的问题.

图1 优化算法的发展历史Fig.1 The history of optimization algorithms

从科学哲学的角度我们十分认同费曼的观点，我们也相信描述自然界基本运动规律的量子力学也能有效的描述优化算法.这一观点并不孤独，2018年11月李国杰院士在《中国计算机学会通讯》上发表了题为《计算机科学基础理论需要重塑》的卷首语，他指出“量子力学改变了传统的逻辑定义，把概率看成了逻辑的内在组成.在计算机领域，构造一台完全公理化驱动的自动机也不现实，而对复杂环境，我们需要放弃严格逻辑而改用概率逻辑”.

对于优化算法的量子化描述我们也经历了长期而曲折的探索，主要分为两个阶段：第一个阶段采用量子谐振子模型构造出多尺度量子谐振子算法，这一阶段我们也陷入到提出新算法的传统思路中，提出了多尺度量子谐振子优化算法，对量子算法的模型和特性进行了初步的探索[11-17]，同时也针对不同的应用场景对算法性能进行了优化[18-21]，解决了组合优化，聚类等多方面的问题[22-29]；第二个阶段我们意识到了提出新优化算法的“盛宴已经结束”，优化算法将进入逐步统一的阶段.这一阶段我们将优化算法的迭代演化过程视为动力学过程，将量子力学作为描述优化算法的理论工具，研究优化算法迭代过程中的动力学行为[30-31].本文也是针对优化算法的量子动力学理论进行的一个初步的探索.

1 优化算法的量子动力学理论

1.1 优化算法的量子动力学方程

从动力学的角度，优化算法的迭代演化过程就是一个运动演化过程，例如遗传算法也可以被视为遗传动力学方法.在量子力学中，最重要、最基本的动力学方程就是Schrödinger方程：

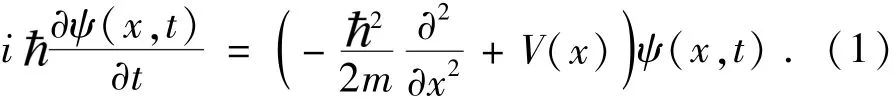
Schrödinger方程的解为波函数ψ(x)，波函数的模方就是粒子位置在空间的概率分布，因此Schrödinger方程描述了粒子位置的概率分布随时间的演化过程.

将优化问题中的目标函数f(x)视为Schrödinger方程中的势能时，即V(x)＝f(x)，可得：

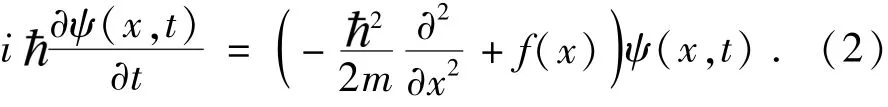
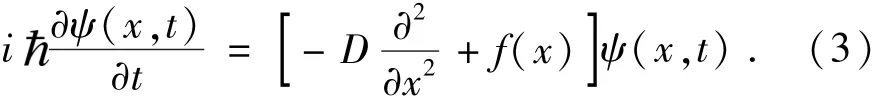
公式(3)就是优化算法的量子动力学方程，这一方程将优化问题转化为了势能f(x)下的约束态量子问题.优化算法迭代过程中，解的概率演化过程被量子动力学方程转化为了波函数模方的演化过程，目标函数的全局最小值问题在量子动力学方程下被转化为了基态波函数模方问题.

1.2 量子动力学下优化算法的基本迭代操作

在优化算法中我们通常将目标函数f(x)视为黑盒函数，因此并不能通过求解优化算法的量子动力学方程来获得基态波函数的模方.同时Schrödinger方程是一个非常难解的方程，只有一些简单的势能才能获得精确的解析解.因此，优化算法量子动力学方程最重要的作用是为研究优化算法提供了一个理论平台.为了从量子动力学方程获得优化算法迭代演化过程中的基本操作，我们将方程中的目标函数分别进行零阶、一阶和二阶Taylor近似，通过不同的近似来剥离优化算法的基本迭代操作.具体的剥离方法如图2所示，图2描述了利用量子动力学作为理论平台获得优化算法基本迭代过程的方法.

根据图2所示，我们可以得到优化算法如下的基本迭代操作：

1)波函数与对应迭代操作

在量子动力学模型下，优化算法的动力学演化过程就是波函数模方的演化过程，波函数的模方就是解的位置的概率分布.依据物理学中的系综理论，可以获得量子动力学中波函数的模方，具体方法是采用多个处于相同状态的粒子以相同方式进行运动，这些相同状态粒子位置的概率分布就是当前波函数的模方.这一认识指出了群体策略是量子动力学下的基本策略之一，优化算法需要采用群体策略来获得对解的位置分布的模拟.

2)目标函数零阶Taylor近似与对应迭代操作

目标函数零阶Taylor近似下的量子动力学方程为自由粒子方程，其方程形式与扩散方程相似.在量子力学中自由粒子的传播子(格林函数)K(x′，x0，t)为正态分布形式：

传播子的物理意义为粒子在t时刻从位置x0到位置x′的概率，这指出了单个采样粒子的采样函数为正态分布.而正态分布的标准差对应于采样的时间间隔，时间间隔长为大尺度采样，获得目标函数的低频信息，时间间隔短为小尺度采样，获得目标函数的高频信息.因此优化算法通常需要进行多尺度的采样过程.由于自由粒子波函数的模方为常数，因此算法在初始化时采用均匀的随机初始化.

3)目标函数一阶Taylor近似与对应迭代操作

目标函数一阶Taylor近似下的量子动力学方程为：

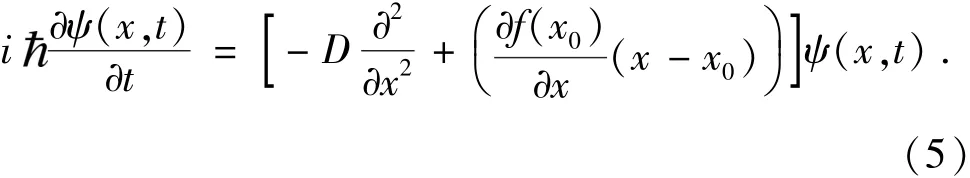
图2 优化算法的量子动力学模型Fig.2 The quantum dynamical model of optimization algorithm

在目标函数为黑盒的情况下，无法获得其精确的导数，只能通过两次采样来获得导数的近似估计，所以上式变为：

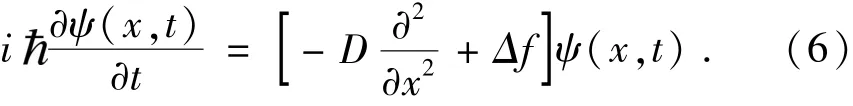
其中Δf为两次采样之间的目标函数值的差，公式(6)被称为采样方程.

当Δf＝f(x′)-f(x0)≤0时，采到更优的解，算法直接接受新解x′

当Δf＝f(x′)-f(x0)＞0时，采到差解，算法估计遇到一个高度为Δf，宽度为Δx＝x′-x0的势垒的阻挡，则采用量子理论中发生隧道效应的透射系数T接受差解，透射系数的计算公式为：

以上采样准则我们称为优化算法的势垒贯穿准则，这是在目标函数一阶Taylor近似下得到的迭代操作.

4)目标函数在极值点的二阶Taylor近似与对应迭代操作

目标函数在极值点的二阶Taylor近似下的量子动力学方程为量子谐振子方程，由于这一方程是在目标函数的极值点附近得到的，因此描述的是优化算法在某一尺度收敛到基态时的操作.由于量子谐振子基态波函数的模方为正态分布，因此在群体策略下只要所有采样粒子的位置分布满足当前尺度的正态分布就可以认为到达了这一尺度下的基态，而所有粒子位置均值就是当前尺度解的数学期望.这表明正态判据和均值替换操作是优化算法算法收敛到基态时的操作.

2 优化算法的基本迭代过程(BIP)

根据优化算法在量子动力学模型下的基本迭代操作可以得到其基本迭代过程(Basic Iteration Process，BIP)，基本迭代过程的流程图如图3.BIP是由k个独立的采样个体构成的多尺度正态群体采样过程.对k个采样个体的位置在定义域中进行随机初始化，然后k个采样个体分别独立的进行正态采样迭代，正态采样的标准差σ初始值可以取的大些，例如取定义域的大小.在采样过程中执行势垒贯穿准则，对于优解直接接受，对于差解按透射系数概率接受.如果k个采样个体的标准差小于当前的正态采样标准差σ，认为算法到达这一尺度的基态，则用k个采样个体位置均值替换其中最差的解，并将所有采样个的正态采样标准差减半，进入下一轮更小尺度的迭代过程.最终，在算法满足最大迭代次数或一定精度后结束.

BIP迭代是基于量子动力学的基本迭代过程，它可以认为是量子动力模型下的骨架算法，也可以作为构造性能更为良好的算法的基础框架，当我们对目标函数给出更多“正确”的估计时，就能获得针对特定估计目标函数性能的提升.

图3 基本迭代过程(BIP)流程图Fig.3 The flow chart of basic iterativeprocess

3 基本迭代过程的性能及波函数模方

3.1 BIP性能实验

量子动力学模型下优化算法的基本迭代过程(BIP)，可以认为是优化算法在量子动力学下的框架算法，为了了解这一基本迭代过程的性能，我们与一些主流算法进行对比.选取了粒子群算法的改进版本(SPSO2011和CLPSO)和烟花算法的骨架版本(BBFWA)与BIP在6个标准测试函数上做性能对比实验，测试函数包括3个多峰函数(F1-F3)和3个单峰函数(F4-F6)，函数的表达式和定义域见表1.

BIP群体的采样个体数量设置为80个，透射系数的计算公式为(在优化问题中我们会减小透射系数)，SPSO2011和CLPSO的群体数量分别设置为30和40；BBFWA的火花数量为300，C r＝0.9、Ca＝1.2；每组实验重复30次，单次实验的最大迭代次数为20 000*D，D为函数维度，实验将函数维度设置为30，实验结果见表2，表中Best表示最优解，Mean和Std分别表示30次重复实验解的平均值和标准差，Sr为30次重复实验的求解成功率，当算法获得的解小于1×10-5时，则判定求解成功.最优的实验结果在表2中用粗体标出.

通过表2可知BIP在3个多峰函数的(F1-F3)的实验中表现出较强的竞争力，30次重复实验解的平均值和求解成功率都优于另外3个算法，在30维的单峰函数优化中成功率均为100%，且求解的最优解和均值都强于SPSO2011.值得注意的是BIP在测试函数Rastrigin(F1)的优化中成功率达到43.33%，其它3组算法成功率均为0.这一结果表明BIP是一种具有竞争力的算法基本框架，也证明了优化算法的量子动力学模型是一种十分有效的理论模型，相比其它自然模型，量子动力学模型的数学和物理含义更清晰、准确.

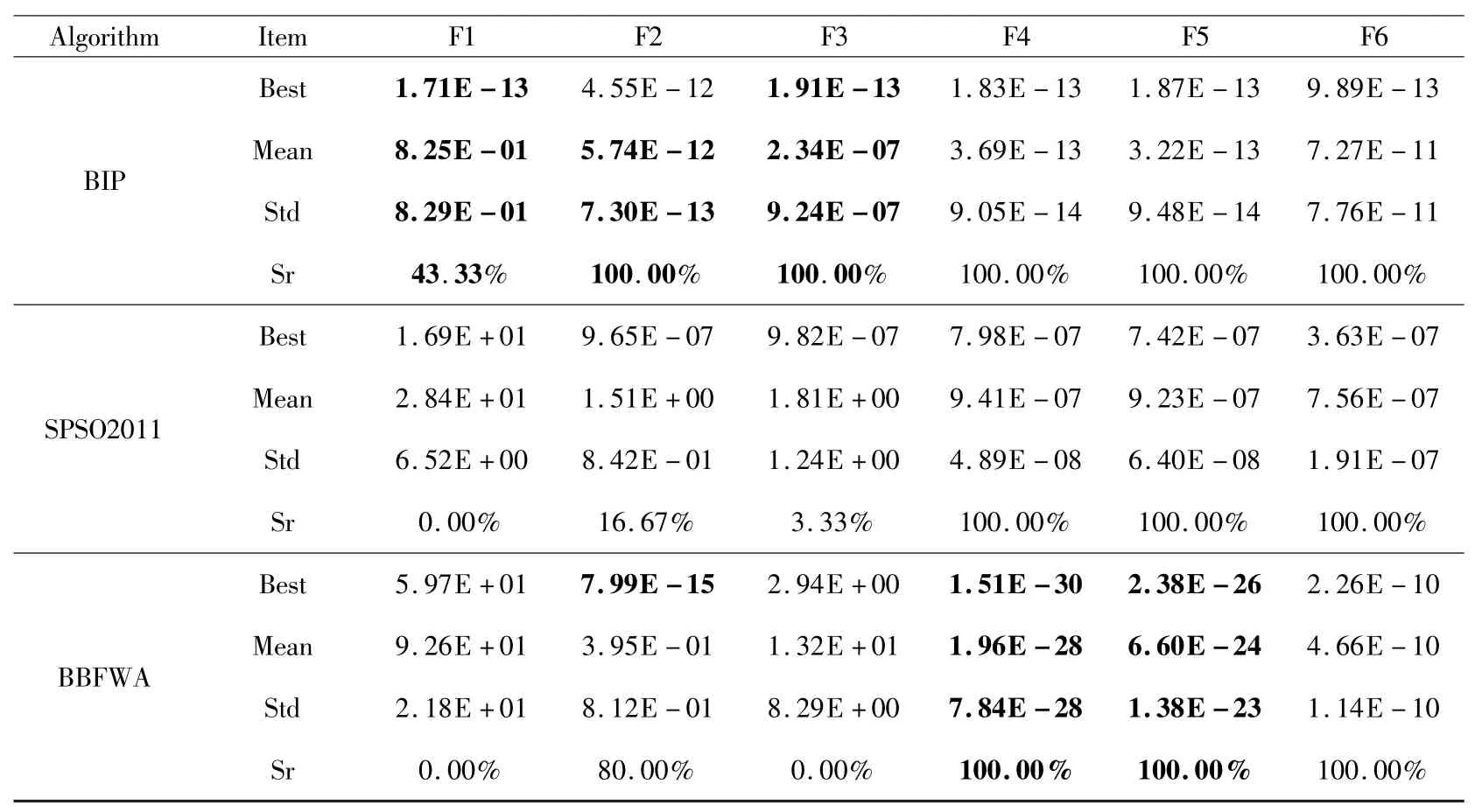
表2 测试函数在维度为30的情况下30次重复实验中各算法的实验结果Table 2 The experimental result of 30 independent runs for each algorithm and benchmark functions，where dimension is 30

3.2 波函数模方的演化实验

量子力学为研究优化算法提供了大量的理论工具，其中波函数的模方就是量子力学中一个最重要的理论工具，在Born对波函数模方的概率解释中，是粒子出现在空间位置的概率分布.类似的，优化算法量子动力学模型下的代表的是当前解位置的概率分布.跟踪和生成方法可以采用系综法，即用群体采样运动中采样个体位置的概率分布来获得.优化算法波函数的模方可以直观的反映算法向全局最优的演化运动过程，这也是量子动力学重要特点.

?

图4 展示了测试函数Rastrigin维度为2，采样个体数为80时，BIP对其优化过程中在不同的迭代次数下波函数模方示意图，图4中Evolution times代表迭代次数，波函数的模方就是解的位置分布的概率密度函数.从图4中可见，随着迭代的进行，波函数模方逐步收敛到全局最优解区域(0，0)附近.量子动力学的演化过程就是波函数的演化过程，通过波函数的模方直观的反映了算法收敛过程中量子动力学的演化过程.

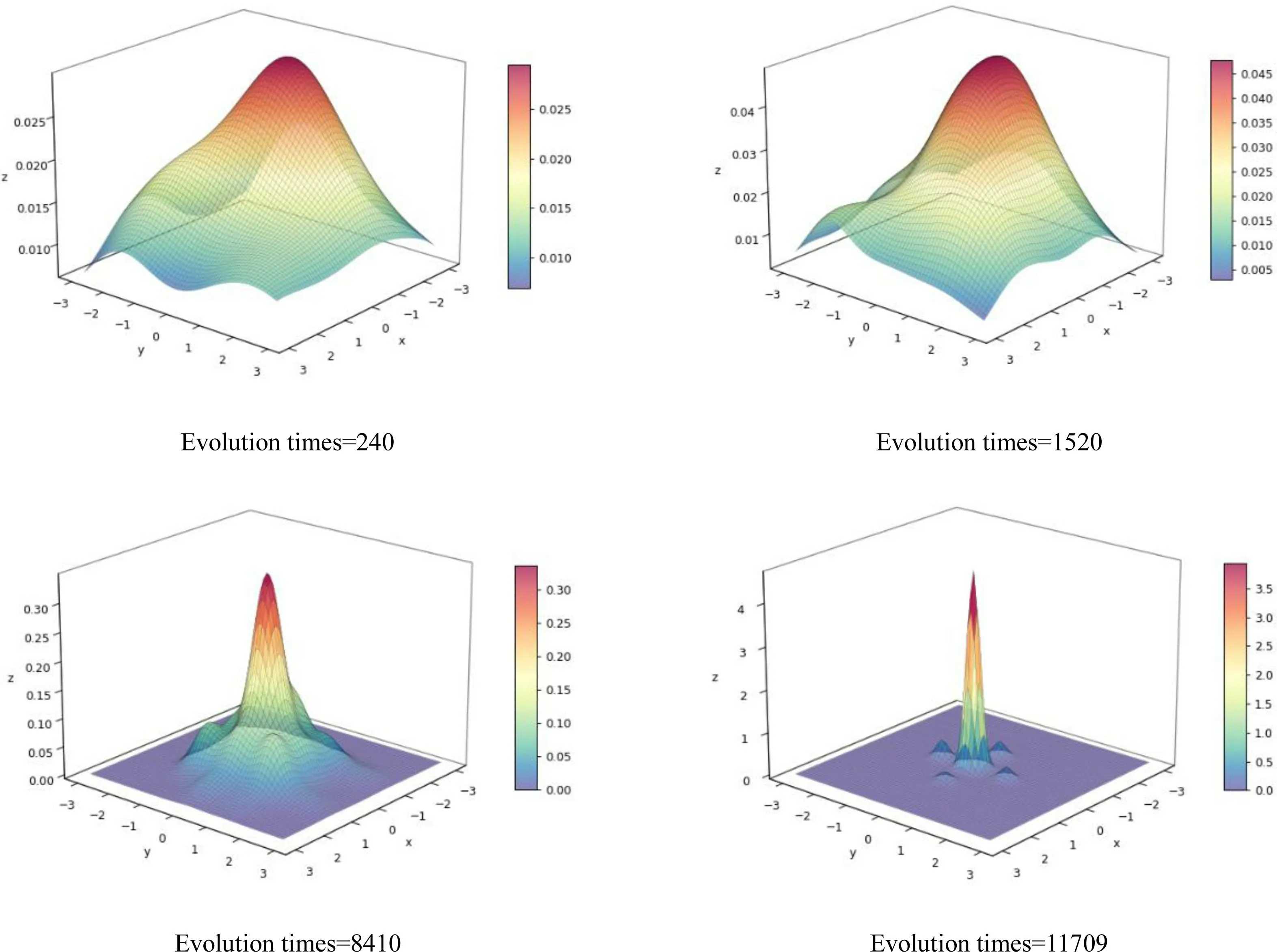
图4 BIP在Rastrigin函数的优化过程中不同迭代次数下的波函数模方图像Fig.4 Demonstration of square of modulus of wave function in the optimization process of BIP on the Rastrigin function

4 结论

本文的工作证明，优化算法的量子动力学理论是一种描述优化算法的有效理论.在量子动力学的理论平台上，可以较为严格的获得优化算法的基本迭代操作和基本迭代过程，反过来这也使得其它优化算法中的一些操作在量子动力学中得到了解释.量子力学经过一百多年无数优秀科学家的努力已具有了非常完备的理论体系，其正确性也得到了大量实验的反复证明，以量子动力学作为解释和研究优化算法的理论模型，有望解决长期以来优化算法领域缺乏完备理论体系的问题，从而推动优化算法成为一门严肃而体系完备的学科.

量子力学是一个理论宝库，有着大量有价值的理论工具，这对于理解、解释和分析优化算法迭代过程中的行为具有重要的价值.我们会继续“固执”的坚持：由于量子力学是一种描述世界基本运动规律的理论，它描述了一种被概率所统治的世界图像，因此量子力学对于解释人工智能具有必然的适用性.目前针对优化算法量子动力学的研究处于萌芽阶段，还有不少重要而有趣的研究工作等待着我们.