超起拉索非保向力作用下伸缩臂几何非线性分析

刘士明，刘俊汝，孟丽霞

（沈阳建筑大学机械工程学院，辽宁 沈阳 110168）

1 引言

全地面起重机作为现代建筑施工中典型的起重设备，其起升高度和工作幅度随着建筑向高耸化发展而不断增加，导致伸缩臂结构的长细比逐渐增大。经典力学中的线性理论分析，在很多种情况下并不适用，因此，在起重臂结构分析时需要考虑几何非线性效应[1]。随着伸缩臂节数的增多其承载能力逐渐变弱，为提高伸缩臂的承载能力使其受力更加合理，引入了附加支撑装置即超起装置[2]。超起装置中由于超起拉索的存在，使得伸缩臂承受非保向力的作用，导致伸缩臂几何非线性变形不能显示精确表达，也缺乏相应的理论推导[3]。文献[4]运用差分法对伸缩臂挠度进行推导，在计算弯矩时略去了轴力的影响，这种方法没有计入轴向力的二阶效应，对大长细比伸缩臂结构存在较大的误差。文献[5-6]分别研究了根部固支和两端铰支两种支撑情况下多节阶梯柱的几何非线性变形问题，得到其臂端部挠度精确表达的递推公式，并给出适合工程实际应用的计算表达式，但没有涉及非保向力作用对多级阶梯柱变形的影响。文献[7-8]建立了空间对称双拉索作用下伸缩臂的挠曲微分方程，虽然考虑了非保向力的作用，为了便于推导，假设多节伸缩臂为等惯性矩，由于简化了推导过程，导致与工程实际差异较大。文献［9-10］利用有限元软件进行建模仿真得到了伸缩主臂的受力状况，缺少深入的理论分析，同时所构建模型也仅仅是针对特定型号，不具有通用性。为此，论文基于纵横弯曲理论，考虑轴向力二阶效应的影响，建立空间对称拉索非保向力作用下多级伸缩臂的挠曲微分方程，求解伸缩臂挠度的递推表达式，为具有超起装置的起重机伸缩臂设计计算提供理论依据。

2 等效力学模型的建立

具有超起装置的典型全地面起重机，如图1 所示。两个对称布置的超起撑杆2 与伸缩臂4 铰接，后拉板3 的一端连接超起撑杆2 的活动端，另一端与伸缩臂4 的基本臂根部铰接，对称布置的超起拉索1 一端连接超起撑杆2，另一端连接伸缩臂4 顶部，变幅油缸5 可以调节起重机的工作角度，后拉板3 和超起拉索1均成对称布置。超起撑杆2、拉板3 以及伸缩臂4 根部构成一个三角形区域，它们对伸缩臂端部的挠曲变形影响很小，因此，在分析伸缩臂的非线性挠曲变形时可以忽略撑杆2 和拉板3 的影响。具有超起装置的全地面起重机伸缩臂可等效为空间对称非保向力作用下的多级阶梯柱模型，如图2 所示。在图2 所示具有超起装置的伸缩臂等效力学模型中，由于油缸的轴向刚度可假设为无穷大，则油缸以下的基本臂与油缸可等效为一个转动刚度为K0的弹性支撑[6]。因此，图2 所示的等效力学模型可进一步等效为弹性支撑条件下的多级阶梯柱模型，如图3 所示。

图1 具有超起装置的全地面起重机Fig.1 All Terrain Crane with Super-Lifting Device

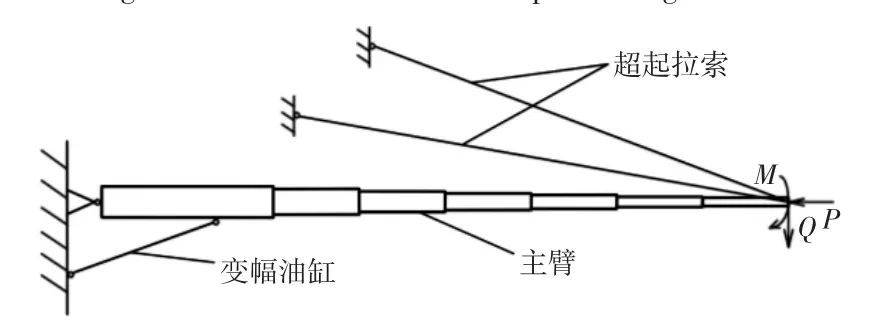
图2 等效力学模型Fig.2 Equivalent Mechanical Model

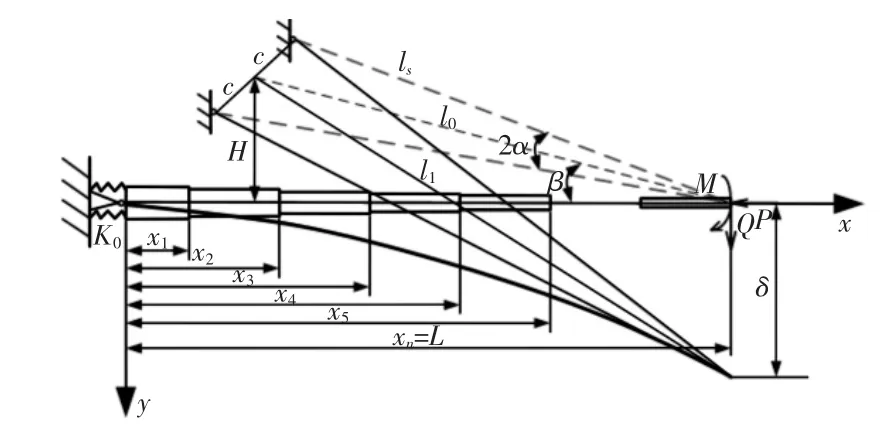
图3 具有超起装置的多级伸缩臂的计算模型Fig.3 Computational Model of Telescopic Arm with Super-Lifting Device

3 伸缩臂几何非线性变形的递推表达式

超起拉索非保向力作用下多级伸缩臂几何非线性分析模型，如图3 所示。两超起拉索的长度均为ls 且对称分布，两牵绳之间夹角为2α，主臂与两拉索所成平面夹角为β，每节伸缩臂的惯性矩为Ii（i＝1，2，3…n），材料的弹性模量为E，在轴向力P、侧向力Q、弯矩M 以及拉索非保向力作用下伸缩臂顶部的竖向挠度为δ。由图3 所示拉索非保向力作用下伸缩臂变形前的几何关系可知：

由于拉索呈对称分布，所以两根拉索产生的合力分解成轴向力Fx与侧向力Fy：

多级伸缩臂自由度挠度表达式（17）是一个关于挠度δ 的超越方程，采用数值迭代的方法解此超越方程即可得伸缩臂自由端的挠度δ。

当无非保向力作用时，Fx、Fy均不存在，伸缩臂自由端挠度表达式（17）可退化成与文献[6]具有相同的表达形式：

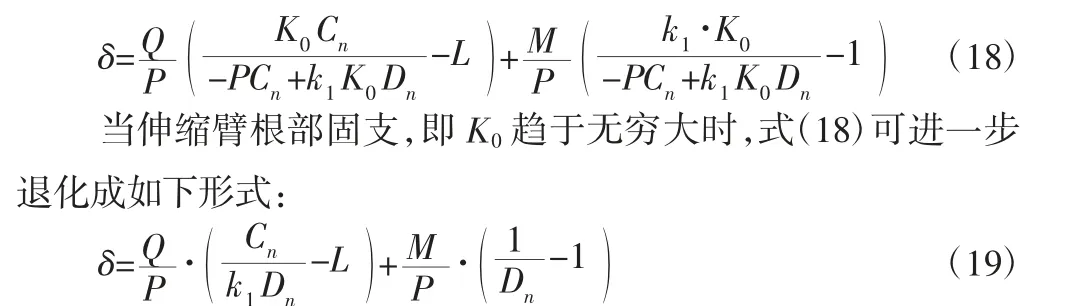
4 算例分析

为了验证所推出的任意多级伸缩臂挠度递推表达式的正确性，对具有超起装置的7 节伸缩臂等效力学模型进行几何非线性分析，并与ANSYS 仿真结果对比，如图4 所示。

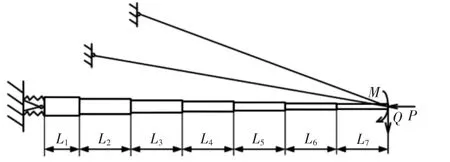
图4 具有超起装置的7 节伸缩臂等效力学模型Fig.4 Mechanical Analysis Model of 7-Section Telescopic Arm with Super-Lifting Device

在如图4 所示弹性支撑的7 节伸缩臂等效力学模型中，主臂弹性模量E＝2×1011Pa，各节臂惯性矩I1＝2.32×10-2m4，I2＝1.63×10-2m4，I3＝1.20×10-2m4，I4＝0.85×10-2m4，I5＝0.62×10-2m4，I6＝0.49×10-2m4，I7＝0.38×10-2m4，各节臂长度为L1＝5.4m，L2＝9.1m，L3＝9.1m，L4＝9.1m，L5＝9.1m，L6＝9.1m，L7＝9.1m。钢丝绳长度ls＝57m，钢丝绳的弹性模量Es＝1×1011Pa，横截面积As＝1×10-3m2。伸缩臂顶部承受的载荷轴力P＝400kN，侧向力Q＝100kN，端部弯矩M＝1000kN·m，α＝5°，β＝10°。ANSYS 仿真验证：对超起拉索作用下伸缩臂结构进行二阶效应的几何非线性分析，在有限元分析中，将每节伸缩臂划分成10 个单元，采用beam44 单元进行建模，用link10 单元模拟单向受拉的超起拉索，弹性支撑用combin14 单元进行模拟。引入ξ＝K0L/（EI1）作为无量纲弹性嵌固系数，在不同ξ 值下，计算结果，如表1所示。其中误差1 表示为ANSYS 线性解与ANSYS 非线性解的误差，误差2 表示理论非线性解与ANSYS 非线性解的误差。

表1 7 节伸缩臂自由端的挠度Tab.1 Free End Deflection of 7-Section Telescopic Arm

从表1 中的误差可以看出，ANSYS 线性解与ANSYS 非线性解的最小误差为8.81%，最大误差为10.12%；理论非线性解与ANSYS 非线性解的误差都在5%以内。算例分析表明：对于大长细比的伸缩臂采用线性分析会引起较大的误差，是不能满足实际工程需要的。因此，对大长细比的伸缩臂进行几何非线性分析才能满足工程实际的设计计算。

5 结论

（1）对超起拉索非保向力作用下多级伸缩臂的受力模型进行合理等效，基于纵横弯曲理论，推导了计及二阶效应的任意多级伸缩臂挠度的递推表达式，获得了伸缩臂几何非线性变形的有效解。（2）对具有超起装置的7 节伸缩臂几何非线性分析表明，论文推导的空间对称双拉索作用下的任意多级伸缩臂挠度的递推表达式是正确的和合理的，能够有效地满足工程实际应用。