基于数形结合思想的初中函数图像教学策略

广东省深圳市深圳中学初中部 黄宜海

函数是发生在集合之间的一种对应关系。定义域、对应关系和值域是函数的三要素。大量的函数可以用图像、表格等形式表示。通过函数图像的教学，能训练学生数形结合的思想方法，学生也能更直观地理解相关知识。在初中阶段抓好函数图像的教学，有利于激发学生学习数学的积极性，也利于与函数有关的知识和技能教学的顺利开展。

一、初中函数图像教学存在的问题

1.对数形结合思想训练的关注度不够

对函数图像和性质这部分内容的教学，要求学生掌握各个函数的相关知识点，并训练学生在解题过程中的数形结合思想，提高理解和应用能力。然而，在实践教学和私下访谈中发现，大部分学生在解答函数题时偏重于函数解析式相关的代数知识的应用，欠缺数形结合的意识，不会结合函数图像去诠释函数的代数问题，进而形成函数复杂，难以理解、掌握的观念。

2.运用函数图像解题能力不足

为了解初中生运用函数图像的解题能力，特意安排笔者所任教的初二、初三学生，用函数图像解题的实验方法，解出以下几道数形结合的经典例题：

（2）已知点K的坐标为（-3，8），求点K在第几象限。

综上实验结果可知，一些学生运用数形结合解题的能力较弱。因此，初中阶段的数学老师要注重在授课中培养学生的数形结合思维，提升其运用数形结合思维解题的能力。

3.函数教学中理论联系实际不紧密

由于函数由定义域、值域和对应法则三要素组成，本身枯燥无味，而函数图像所蕴含的信息较多且具有隐蔽性，如果脱离了实际生活，初中生就难以理解，难以激发其学习函数的兴趣。从当前的函数图像教学的教材内容来看，初中阶段还是较偏重基础知识、函数的性质、函数图像的增减和坐标轴之间的关系之类的理论知识，与生活实际联系不够紧密，学生就会认为“所学无所用”，或者因其较为抽象、难以理解，进而产生厌学现象。

二、数形结合的初中函数图像教学策略

1.灵活利用几何画板教学

一次函数、反比例函数和二次函数是初中数学学习阶段三类重要的函数。一次函数和反比例函数较容易理解，但二次函数情况较为复杂。传统的课堂静态教学，授课是以课本和黑板的板书为主，很难将二次函数的解析式、图像及其性质有效结合，并通过函数图像变化的形式演示出来，让学生来理解。随着信息科技的进步，几何画板被研发出来作为新的信息教学软件，教师只要把函数解析式输入软件中，通过程序的快速运行就可以自动生成直观的、动态的函数图像，且方便教师生动形象地将相关知识传授给学生，增加了师生之间的互动，让枯燥的知识趣味化，容易激发学生学习的兴趣，提升学习的积极性。

2.加强学生精准作图的能力，培养学生数形结合的解题能力

一次函数的图像为一条直线；反比例函数的图像是双曲线；二次函数的图像为一条抛物线。一次函数和反比例函数较容易被理解。二次函数由于其形式多样，对于初中生来说较难理解和应用。若将函数的性质用图像精确表达，则可以帮助学生直观地理解。如，对于二次函数而言，其一般式y=ax2+bx+c中包含了三个参数a，b，c，单纯的语言描述不能很好地说明这三个参数的变化对函数图像产生的影响，学生不知道如何去理解，但将一般式用配方的方法转化为顶点式，再依据函数的变化描绘出函数图像，就很容易直观地看出图像的对称轴、顶点坐标和单调性。

例：已知抛物线y=x2+bx+8和平面直角坐标系的x轴相交，两个交点分别为A与B，它与y轴的交点为C。其中，点B的坐标为（4，0），求三角形ABC的面积。

解题思路：若要解出三角形ABC的面积，必先依据已知条件作图，并用待定系数法将B（4，0）代入抛物线的解析式中得：0=16+4b+8 ，求出b=-6，进而推导出抛物线的解析式为y=x2-6x+8， 再将其转化为交点式：y=(x-2)(x-4)，所以点A的坐标为（2，0），点C的坐标为（0，8），画出二次函数y=x2-6x+8的图像，将点A、B、C连成三角形，如下图所示：

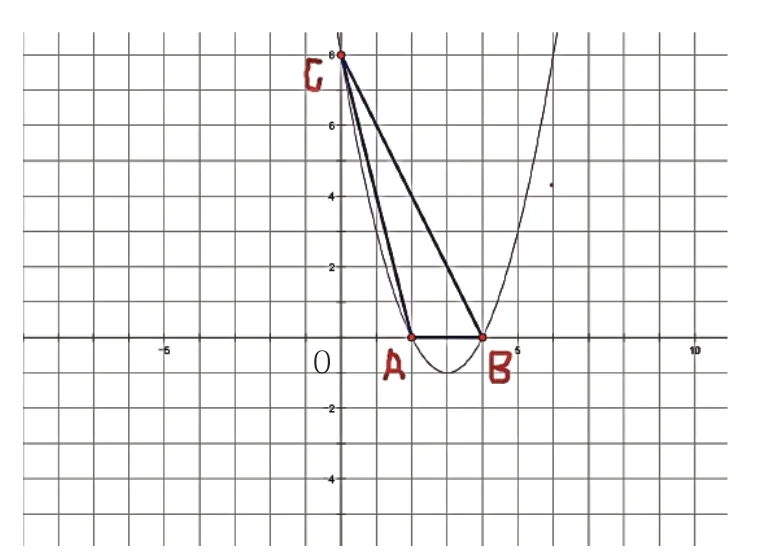
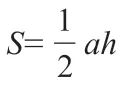
3.教学中注重理论与实践相结合的方法

当前，素质教育已深入人心，中考试题也越来越贴近实际生活。鉴于此，在初中数学教学中，将函数理论与实践相结合起来开展教学，可依据现实情况的限制条件和函数的变化来帮助做决策，学生也更容易理解。教师在教学过程中要重视理论与实际相结合的教学方法，强调数形结合的解题思想，通过情景导入，激发学生学习的主动性，主动动手动脑，学会科学理性地解决生活中的难题。

一次函数、二次函数和反函数的图像与性质是初中阶段学生学习的难点。在教学的过程中，教师有意识地培养学生数形结合的思维能力、逻辑思维能力和综合实际应用能力等，有助于学生将数学抽象的概念更为具象化地思考，感知数学的力量。