创新教学策略,提升初中数学课堂效率
浙江省义乌市佛堂镇初级中学 王 妃
数学老师要在明确教学目标的基础上,解决“如何创新教”的问题。为此,数学老师应当把握一个原则:学为主体,教为主导,疑为主轴,动为主线,同时创新教学策略,创新课堂推进形式,创新教学机制。
一、创新教学理念,教学联系生活
数学教学正处于不断改革和发展中,新时代教育也向初中数学老师提出了很多新的要求和准则,数学老师应当从这些新的标准出发,构建高效数学课堂。
数学是一门逻辑性比较强的学科,它的产生来源于生活中的问题,而它的作用是解决生活中的问题。将教学和生活相联系,能够引发学生的代入感和共鸣感,从而弱化该门学科逻辑性强、复杂、难理解的特点。例如,浙教版初中数学《一元一次方程的应用》这一节课的学习,老师在备课的时候准备了两道课堂练习题。
课堂练习1:如图1,一纪念碑建筑的底面呈正方形,其四周铺上花岗岩,形成一个宽为3米的正方形边框,已知铺这个边框恰好用了192块边长为0.75米的正方形花岗岩,则纪念碑底面的边长是多少米?
课堂练习2:如图2,用x表示中间空白正方形的边长,怎样用含x的代数式表示阴影部分的面积呢?
第一个问题和学生生活相联系,生活中处处可见的问题易于学生理解,而第二个问题把数学的学科特点表现得非常明显。“x”“空白正方形”“边长”“面积”“阴影部分”,这些都是数学学科中的特有名词。正是因为这样,有些学生一开始就觉得第二个问题复杂、难解,不愿意动脑筋解决,而第一个问题和自己的生活贴近,愿意尝试解决问题。它的边长是怎么算的?用我们原先学习过的方法可不可以算?如果不可以,应该怎么解决?学生会绞尽脑汁地思考问题,因为他们觉得自己有能力解决这种问题。教学和生活相联系,生活化的气息可以弱化学科的特点,让学生克服畏难心理。
二、创新教学方法,借助网络工具
教学应当与时俱进,教师准备的教学材料应当体现“新颖”的特点,不妨运用时代发展的产物造福学生,给学生带来不一样的学习体验。比如,老师可以下载一些和学习有关的软件,拓宽学生的视野,缓解学生的学习压力。
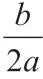
三、创新反馈机制,增加师生互动
为了提高课堂的教学效率,活跃课堂氛围是一个必不可少的环节。本文认为,活跃课堂氛围有两个主要途径:第一,创新反馈机制;第二,增加师生互动。如此,课堂就会变得活跃起来。
增加师生互动的方法有很多。老师在课堂上可以多设置一些数学问题,老师多问,学生自然也会多答。老师还可以设置一些游戏,学生在玩游戏的过程中心情十分放松,思维也活跃起来,和老师之间的互动自然会增多。与此同时,老师还可以开展小组学习、自主学习的学习方式。当学生学习遇到困难时,就会向同学和老师请教,师生的互动也会增加。例如,初中数学《条形统计图和折线统计图》这一节的学习,老师设置了一个任务由小组同学合作完成:“基因的发现是20世纪生物领域的一项重要成就,探索生命奥秘的基因工程由此得到了飞速发展。表中的数据表示稻米、人类、拟南芥植物、蠕虫、果蝇、流感病毒的基因数量,请根据表中的数据画出相应的条形统计图和折线统计图,并归纳两个统计图的特点。”

干生物人类稻米蠕虫拟南芥植物果蝇流感病毒人与若基因数量(个)30000 50000 17800 25500 13600 1750
不少小组在解题的过程中都遇到了问题,纷纷向老师请教,比如:我应当如何选择纵坐标的刻度呢?我现在已经画出了条形统计图和折线统计图,可是我也没有发现二者的特点呀?对此,老师并没有直接回答学生的问题,而是给予提示,让学生继续思考:“你先观察一下表格中的5个数据,看看它们之间的差值大约是多少,然后再来决定你选择的刻度。”“如果想要知道条形统计图和折线统计图各自的特点,首先不妨比较它们的不同点和相同点,它们的不同点肯定就是它们的特点。”在问答中,老师成为学生的学习伙伴,这就是加强师生互动的好处。
对于反馈机制,本文提倡老师采用匿名反馈的方式,让学生大胆地说出自己听课的感受,对老师的教学提供一些意见。这样既节约了课堂的时间,老师又能够及时地看到自己在教学中的不足。教学也是老师和学生互相磨合、互相适应的过程。学生适应老师的讲课方式,老师知道学生的基本情况,二者互相配合,共同努力,才能够完成好学科的教学与学习。
仔细分析初中数学这门学科,基础内容比较多,知识点之间的跨度较大,所以整体难度不可小觑。今后数学老师在开展教学工作的时候,就可以从教学理念、教学方式和教学机制这三个方面入手进行创新,把握一定的方向,努力提升初中数学的课堂教学效率。

