Standing window of oblique detonation with pathological behaviour

Zhuo XU, Gng DONG,*, Zhenhu PAN, Mingyue GUI,c

a Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China

b School of Energy Resources and Power Engineering, Jiangsu University, Zhenjiang 212013, China

c State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

KEYWORDS Chemical reaction;Equivalent parameter;Hypersonic flow;Oblique detonation;Pathological detonation;Standing window

Abstract Standing of an Oblique Detonation Wave (ODW) on a wedge within combustor is the prerequisite of thrust generation for ODW engine which is regarded as a novel and conceptual propulsion device with hypersonic flight Mach number. Usually a standing window of ODW is defined as the wedge angle ranged from the ODW detached angle from wedge (upper limit) to the angle that a Chapman-Jouguet (CJ) detonation occurs (lower limit). For pathological detonation cases,however,the CJ detonation cannot be achieved,and thus the lower limit of the standing window of ODW should be revisited.In present study,two types of reactions in hypersonic incoming flow that include the behavior of pathological detonation, that is, the single-step irreversible reaction with mole variation and the two-step irreversible reactions with exothermic process followed by endothermic process,have been used for studying standing behavior of ODW.The steady detonation polar analysis of ODW is carried out for both reaction systems. The results reveal that the reaction with more mole decrement and the reactions with stronger endothermic process show the pathological detonation feature and therefore modify the lower limit of standing window of ODW. Three equivalent parameters are proposed to quantitatively measure the standing window range of ODW from points of view of thermodynamics, Mach number of incoming flow and heat effect of reactions.It is found that the standing window of ODW is determined by the specific heat ratio,the overdrive degree of detonation and the endothermic level of the hypersonic incoming flow,regardless of whether the detonation is pathological or not.

1. Introduction

When a combustible premixed gas with a hypersonic velocity impacts on a wedge with a turning angle of θ,a standing Oblique Detonation Wave (ODW) with an angle of β can form.The exothermic expansion of combustion products through the ODW can generate the thrust in high combustion efficiency.Therefore,the ODW engine is regarded as a promising propulsion device that offers higher flight Mach number than traditional scramjet.1-6A prerequisite of thrust generation in ODW engine is that the ODW must steadily stand facing the hypersonic incoming flow within the combustor. Thus, the study on standing condition of the ODW is important for fundamental and practical purposes.

Maybe the early study focusing on the standing condition of ODW comes from work by Gross.7He presented a detonation polar that describes the relationship between the detonation wave angle β and the wedge angle θ by using the ODW jump condition. Further, Pratt et al.8studied the detonation polar and pointed out that ODW can be divided into three branches in the detonation polar diagram,that is,weak underdriven branch,weak overdriven branch and strong overdriven branch. They then defined a standing window represented by the range of wedge angle that satisfies θCJ≤θ ≤θmax. Here θmaxis the upper limit of standing window and corresponds to the wave detachment angle from wedge which is the boundary between the weak and strong overdriven ODW branches,while θCJis the lower limit of standing window and corresponds to the wedge angle at a Chapman-Jouguet(CJ)detonation state which is the boundary between weak overdriven and weak underdriven ODW branches. For an ideal detonation,the weak underdriven ODW is not admitted when θ ＜θCJ.If the weak underdriven ODW is admitted, the chemical reaction has to cross the sonic state(CJ state)and end at the supersonic zone, this means that an irreversible reaction must pass through the state of maximum entropy (CJ state) along the Rayleigh process and therefore violates the second law of thermodynamics.9However,for a pathological detonation where a classical CJ detonation cannot be realizable, for example, in the reaction system including the endothermic steps or the mole decrement of products,10it is impossible for lower limit of the standing window to fall into CJ state. Powers et al.11,12studied the reaction zone structure of the weak underdriven ODW for the two-reaction system with endothermic step.They revealed that the weak underdriven solution can be admitted,implying that the lower limit of the standing window can extend to the weak underdriven ODW branch. The existence of pathological detonation had been verified experimentally by Dionne et al.,13and the stability of this type of detonation had also been studied numerically by Sharpe and Falle14and Dionne et al.15

It should be noted that existence of the Taylor wave,which occurs immediately downstream of the reaction zone of ODW,16also alters the lower limit of standing window by lowering θ below θCJ. The feature of Taylor wave in the oblique detonations has been studied theoretically and numerically.17,18Essentially, the Taylor wave is a centered Prandtl-Meyer expansion fan behind the reaction zone of ODW that matches the flow angle with the wedge angle. The matching of the flow can lead to the stabilization of ODW even if θ is less than θCJ. Unlike the feature of weak underdriven ODW,the Taylor wave can hold the wave β at its classical CJ value in the underdriven regime(θ ＜θCJ)by matching the flow field behind the ODW. Therefore, the variation of lower limit of standing window in this case is due to the aerodynamical behavior and does not violate the second law of thermodynamics.Although it is believed that combination or competition of both features is important for understanding and designing ODW engine, the effect of pathological detonation involved in chemical reactions on standing behavior of ODW is hardly reported and thus firstly needs to be clarified alone.

In this study, we focus on the effects of reaction types on the standing window of ODW, based on a steady detonation polar theory for perfect ideal gas.Following Fickett&Davis10and Lee,19we chose two types of irreversible reactions:one is a single-step and exothermic reaction with mole variation, and the other is two-step reactions (an exothermic reaction followed by an endothermic reaction).For the first reaction type,the variation of mole number from reactant to product can lead to the change of specific heat ratio of the system, which has the practical applications as the fuel/oxide mixture (for example, stoichiometric 2H2+O2system). In particular,when the significance decrease of species mole number occurs during the reaction,this system can show the pathological detonations.The second reaction type seems less realistic for current ODW propulsion; however, it represents another pathological detonation behavior for some complex reaction system (for example, H2-Cl2system13) that is fundamentally significant and maybe has possible future applications in ODW propulsion system. In present study, the standing windows of both reaction systems are determined under the conditions of either classified CJ detonation or pathological detonation. Several equivalent parameters are proposed to describe the standing behavior of ODW from different aspects,such as, thermodynamics, Mach number and heat release of the reactively incoming flow. Note that although the real ODW is inherently multi-dimensional and often unsteady,20-22it must be stood for its practical use. This suggests that a standing ODW statistically has a fixed wave angle β which should obey the relationship with wedge angle θ through a detonation polar relation. Therefore, a one-dimensional and steady detonation polar analysis is applied in present study.

2. Steady analysis and chemical reactions

2.1. Oblique detonation polar

The schematic of ODW is illustrated in Fig. 1. Assuming a reactively and calorically perfect ideal gas in present study,and setting 0 and 1 as the states before and behind the ODW respectively, the relationship between the ODW angle,β, and the wedge angle, θ, can be given in terms of the Rankine-Hugoniot relation

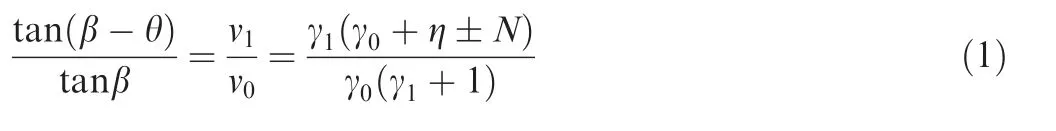
where

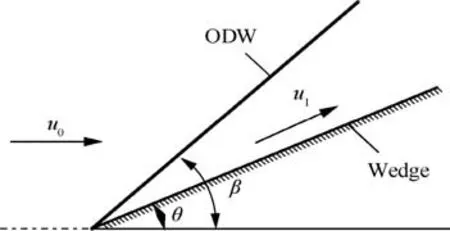
Fig. 1 Schematic of oblique detonation wave.

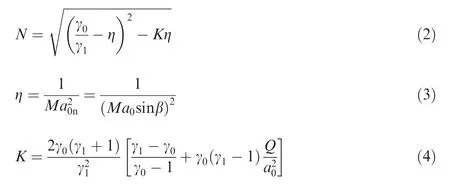
In Eqs. (1)--(4), v0and v1are the specific volumes before and behind the ODW, respectively; γ0and γ1are the specific heat ratios before and behind the ODW, respectively; Ma0denotes the Mach number of incoming flow, Ma0=u0/a0,and u0and a0are the particle velocity and the sonic speed of incoming flow, respectively; Ma0ndenotes the Mach number component normal to the front of the ODW;Q is the chemical heat release(Q ＞0 if the heat is released to the environment).Eq. (1) gives the oblique detonation polar which is deduced from one-dimensional governing equations of fluid flow and the geometry of flow velocity. Because no other assumptions are introduced, Eq. (1) is universal even though the chemical reaction in the fluid is endothermic, which will be employed in present study.

2.2. Reaction with a mole variation

In the reactive flow,a single-step and irreversible reaction with heat release of Q can be expressed as

where δ is a coefficient representing a mole variation from product B to reactant A. 0 ＜δ ＜1 denotes a reaction with a mole decrement, while δ ＜0 denotes a reaction with a mole increase. If defining λ as the progress variable of the reaction,we have YA=1-λ,YB=λ,Cp=CpA+λ(CpB-CpA)and WA=(1-δ)WB, where YAand YBare the mass fractions of species A and B,respectively;CpA,CpBand Cpare the specific heats at constant pressure of species A,B and mixture,respectively;WAand WBare the molecular weights of species A and B, respectively.

When the reaction is in progress with λ, the specific heat ratio of the mixture can be written as

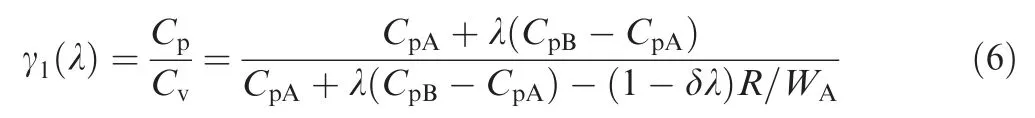
where Cvis the specific heat of mixture at constant volume,and R is the universal gas constant.

Setting α=CpB/CpAin Eq. (6) yields

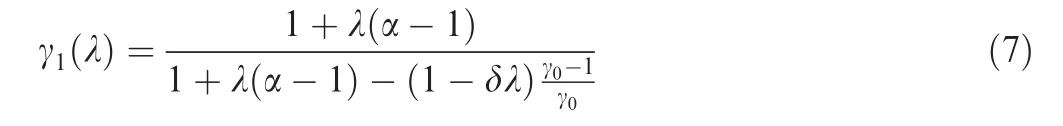
where γ0=CpA/CvA.Substituting Eq.(7)into Eqs.(1),(2)and(4),thus Eq.(1)represents the effect of reaction Eq.(5)on the detonation polar.

To examine the detonation features of reaction with a mole variation, we introduce the thermicity (Σ) that is defined as10

where σ denotes the energy release coefficient that is expressed as σ=Δn/n+Q/(TCp),in which n and Δn are the total number of reaction and the mole change in the reaction, respectively, and T denotes the temperature of the system; Σ represents the transformation of chemical energy into energies of heat and motion10. Thus, the positive Σ corresponds to an ideal detonation while the negative Σ corresponds to a pathological detonation. For reaction Eq. (5) with a reaction progress λ, we have Δn=-δ and n=1-λδ, and then σ can be further expressed as

Therefore, the first term in the right hand of Eq. (9) (-δ/(1-λδ)) is negative for the reaction with a mole decrement(0 ＜δ ＜1). Once the negative value of the first term exceeds the positive value of the second term in the right hand of Eq.(9), a negative σ and Σ can be obtained and the pathological detonation occurs.

2.3. Reactions with endothermic step

The two-step and irreversible reactions first suggested by Fickett and Davis10are considered in this section. The reactions I and II are expressed as

In the above reactions,the progress variables λIand λIIfor reactions I and II are defined as dλI=-dYA(0 ≤λI≤1)and dλII=dYC(0 ≤λII≤1), respectively. When the reactions occur, the mass fractions of species A, B and C are denoted as YA=1-λI, YB=λI-λIIand YC=λII, respectively.

Assume that reaction rate of λIand λIIcan be expressed as the following form:

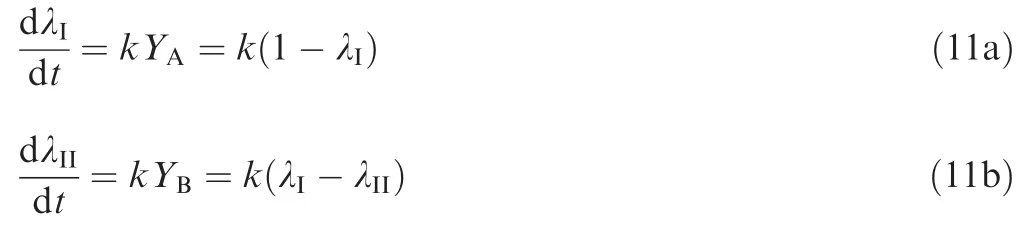
where k is the reaction rate constant,and dividing Eq.(11b)by Eq. (11a) gives

Taking initial condition, λII|λI=0, into consideration, we can integrate Eq. (12) to obtain a reaction path equation in λI-λIIplane as follows:

We now define QIand QIIas the heat release in exothermic reaction A →B and the heat absorbing in endothermic reaction B →C, respectively, and then set QI＞0, QII＜0 and |QI|＞|QII|. Thus, a total chemical heat release Q can be expressed as

Especially, when both reactions have completed(λI=λII=1), Eq. (14) becomes

Note that Q is not monotonic function of λIin Eq. (14),substituting Eq. (13) into Eq. (14) and then differentiating Eq. (14) with respect to λ1give the following equation:

Taking the extreme value for Eq. (16) produces λI=1-eQI/QIIand substituting it into Eq. (14) yields

where Qmaxdenotes the maximum chemical heat release during the reactions. Eqs. (14), (15) and (17) represent several heat release forms that affect the detonation polar through Q in Eq. (4).

For two-step reactions Eq. (10), the thermicity Σ is expressed as10

where σIand σIIdenote the energy release coefficients for reactions with λIand λII, respectively, and are given by

Thus, the negative QIIleads to the negative σIIwhich may result in the pathological detonation behavior with negative Σ in Eq. (18).

3. Results and discussion

3.1. Standing window of pathologically oblique detonation

For the single-step irreversible reaction in Eq.(5),δ ≤0 represents an ideal detonation in which the mole number does not decrease during the reaction.Fig.2 shows the detonation polar with δ=0 (dashed curve) based on Eq. (1) for case of α=1,Q=50RT0, γ0=1.2 and Ma0=8.0, where T0is the static temperature of incoming flow. Here θmaxis the maximum wedge angle (upper limit) that the ODW is detached from the wedge, and θCJis the minimum wedge angle (lower limit)that a Chapman-Jouguet (CJ) detonation occurs. Thus a standing window, Δθ, that is, the range of angle of wedge for the ODW that can be attached on the wedge, is expressed as Δθ=θmax-θCJfor δ=0 case, as shown in Fig. 2.

Fig.2 Detonation polars with different δ for α=1,Q=50RT0,γ0=1.2 and Ma0=8.0.

When 0 ＜δ ＜1 for reaction in Eq. (5), the detonation may be pathological due to the mole decrement during the reaction.10,19In this case, the detonation polar is varied due to the effect of δ on γ1in Eq. (7). The solid curve in Fig. 2 describes the detonation polar at δ=0.7. On this curve, θWand θSare the wedge angles corresponded to the weak and strong solutions of detonations, respectively. Note that θCJis actually unadmitted because a pathological detonation appears, and therefore, the standing window is no longer expressed by θmax-θCJ. Fig. 3(a) shows the Hugoniot curves with different progress variables(λ=0,0.6 and 1.0)and Rayleigh lines with different propagating Mach numbers of detonation wave in p-v plane for the reaction of δ=0.7, here p and v denotes the pressure and specific volume, respectively.It can be seen that the Hugoniot curves do not monotonically rank along λ. The Hugoniot curve with λ=0.6 (bold solid curve) locates at the top right of that with λ=1.0 (bold dashed curve). Thus, there exists a point P (also called generalized CJ point)on the Hugoniot curve with λ=0.6,at which the sonic flow and the zero of thermicity can be reached simultaneously but the reaction is still in progress(λ ≠1). Once the reaction reaches the point P along the Rayleigh line that is tangent to the Hugoniot curve of λ=0.6,it continues to go to the point S or point W at which the reaction completes. Point W shows a weak detonation solution,in which the particle velocity is supersonic beyond the sonic point P within the reaction zone, while point S corresponds to a strong detonation solution, in which the particle velocity is always subsonic within the reaction zone. Fig. 3(a) also shows that the Mach number of weak detonation wave (MaP=3.38) is larger than the Mach number of CJ detonation wave (MaCJ=2.85), and the latter is actually unrealizable because the Rayleigh line including point CJ (dashed line) cannot pass through entire Hugoniot curve cluster from λ=0 to λ=1.

Fig. 3(b) depicts the relationship between v/v0and θ based on Eq. (1) for case of δ=0.7 at λ=1. We can find θW＜θCJ＜θSand that the realizable range of standing window is θmax-θSor θmax-θWwhen the final state of reaction is reached. Whether point S or point W is taken as the final state of the reaction depends on the rear boundary condition of the detonation.For the ODW case,the rear boundary condition is the wedge wall which is like a movable piston,and the profile of wedge wall determines the piston velocity.Therefore,the state of point W is similar to a piston problem with certain piston speed that may lead to the occurrence of the weak solution.10Note that the point W can stably exist by matching the rear boundary condition with weak solution state through the rarefaction waves (Taylor waves). Also, Powers and Gonthier11have demonstrated that the weak underdriven branch in the detonation polar is admitted for pathological detonation.Therefore,the lower limit of the standing window for this type of detonation can be extended to θW, and subsequently leads to the increase of the window (see Δθ of δ=0.7 case in Fig. 2). Based on the above analysis, the determination of standing window for ODW not only depends on the specific heat ratio of reaction system (Eq. (7)) but also depends on the lower limit of the standing ODW.

3.2. Thermodynamic effects analysis

In this section,we focus on the single-step irreversible reaction of Eq. (5). Since the variations of both δ in Eq. (5) and α=CpB/CpAcharacter the change of specific heat ratio in system (see Eq. (7)), parameters δ and α can be regarded as the indicators of thermodynamic properties of the system. This section examines the effect of both parameters on the standing window feature of ODW.

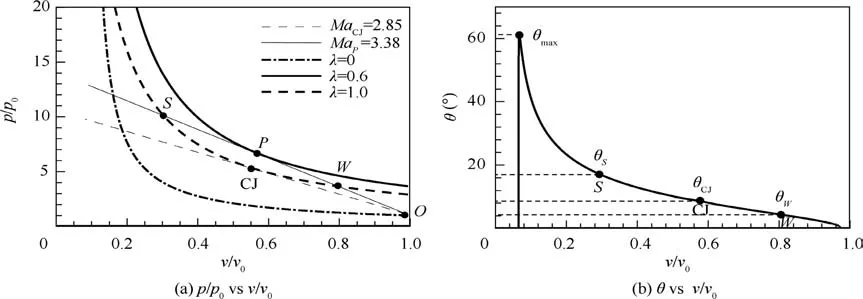
Fig. 3 Variation of p/p0 and wedge angle θ with v/v0 for α=1, δ=0.7, Q=50RT0 and γ0=1.2.

For fixed parameters γ0=1.2,Q=50RT0and Ma0=8.0,we calculated the detonation polars with various δ and α.Fig. 4 gives the series of θ-δ curves at the different values of α. Here the bold and the thin curves denote the upper and lower limits of θ respectively for each α case.It can be observed that larger δ or α gives larger standing window of ODW. The subfigure in Fig. 4 shows that the lower limit of standing window becomes bent downward for pathological detonation,compared with that for classical CJ detonation case, when δ is larger than 0.4 for α=1.0 case. Actually, for all α cases,the lower limits of standing window show the bending downward when δ is larger than 0.3-0.5, suggesting that the mole decrement of the reaction leads to the pathological detonation extending the lower limit of the standing window of ODW.

Because of the similarity of curves with varied α in Fig. 4,we can collapse these curves into one by proposing an equivalent thermodynamic parameter, δ～=(α + δ - 1)/α. The equivalent reflects the influence of specific heat ratio γ1on the standing behavior of ODW. Taking λ=1, we substitute the equivalent parameter δ～into Eq. (7) to obtain the following expression:

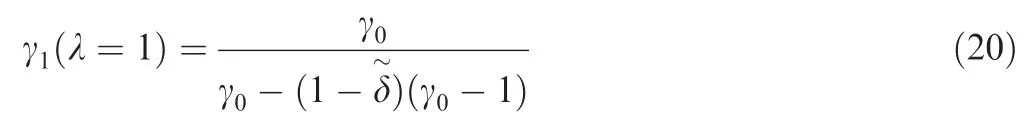
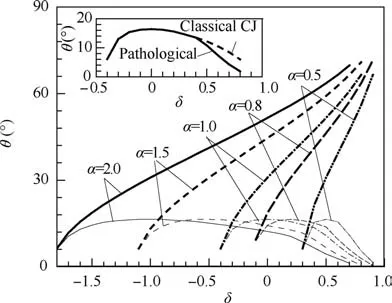
Fig. 4 θ-δ diagrams at different values of α.

3.3. Flow Mach number analysis

Further, we explore the standing window of ODW by varying the Mach number of incoming flow (Ma0) and fixing α=1.0=δ).Fig.6 depicts the θ-δ curves with three Mach numbers of incoming flow, Ma0=7.0, 8.0 and 9.0. It can be seen that larger Ma0or larger δ results in wider standing window of ODW. Again, due to the similar curves with different values of Ma0, we collapse the curves into one by proposing a flow equivalent parameter Ma0/MaP, and here MaPdenotes the Mach number of detonation wave propagation at the generalized CJ point (point P). Fig. 7 shows the relationship between MaPand Mach number for CJ detonation wave propagation(MaCJ) when δ varies. It can be found that MaPis just the same as MaCJand the pathological detonation does not occur when δ ≤0.5.Once δ ＞0.5,MaCJbecomes less than MaPand is unrealizable. In this case, the CJ detonation is replaced by the pathological detonation.

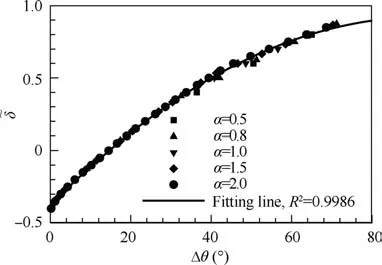
Fig.5 Standing window Δθ for equivalent reaction parameter

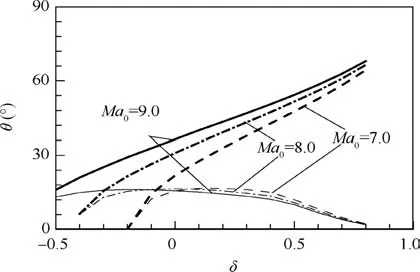
Fig.6 θ-δ diagrams at different values of Ma0(bold curves and thin curves denote upper limit and lower limit of standing windows, respectively, α=1.0).

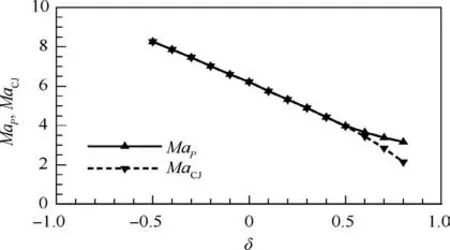
Fig. 7 Mach numbers of CJ detonation and generalized CJ(point P) detonation with different values of δ (α=1.0).

Fig. 8 gives the correlation between Δθ and Ma0/MaPfor case of α=1.0. The quadratic fit between them gives a good correlation with R2=0.9596. Note that Ma0/MaPhas the implication of overdrive degree of detonation wave which is defined as f=(D/DCJ)2,18where D and DCJdenote the velocities of overdriven detonation front and CJ detonation front,respectively. Therefore, the flow equivalent parameter means that stronger overdrive degree for ODW can produce the wider standing window regardless of Mach number of incoming flow and detonation type (pathological or CJ detonations).

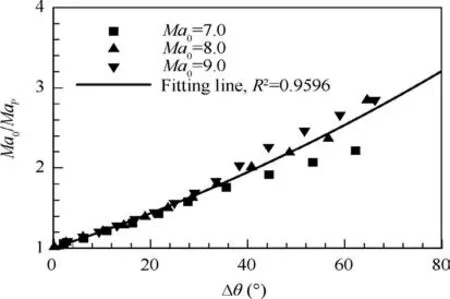
Fig.8 Standing window Δθ for equivalent flow parameters Ma0/MaP

3.4. Heat effect analysis

In the above sections, a single-step irreversible reaction with mole variation is employed to examine the effect of thermodynamic and flow properties on the standing window of ODW.As a matter of fact,the two-step irreversible reactions involved in endothermic process,Eq.(10),show the similar effect.Fig.9 presents the Hugoniot curves for cases of Q=0 at λI=λII=0, Qλ=1=50RT0and Qmax=56.8RT0in p-v plane, by setting QI=100RT0and QII=-50RT0. Similar to that in Fig. 3(a), the Hugoniot curve with Qmaxlocates at the top right of that with Qλ=1. As a result, the final state of the detonation also falls into the point W (weak detonation solution) along the Rayleigh line with MaP=6.60. Again,the CJ detonation with MaCJ=6.22 is unrealizable due to the same reason as that in Fig. 3(a).

Substituting Eqs. (15) and (17) into Eq. (21) yields

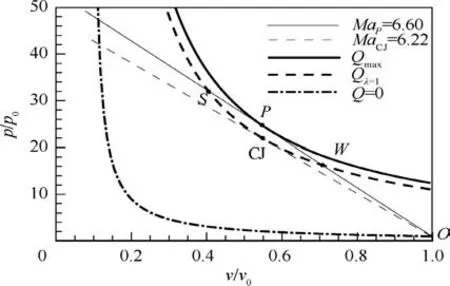
Fig. 9 Variation of p/p0 with v/v0 for α=1, δ=0, QI=100-RT0, QII=-50RT0 and γ0=1.2.

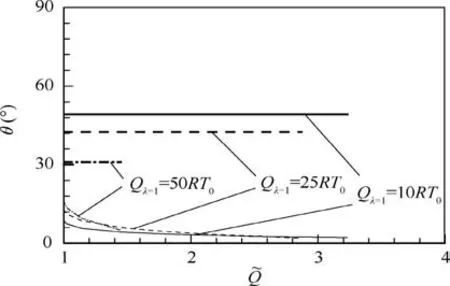
Fig. 10 θ-diagrams at different values of Qλ=1.

Fig. 10 shows the variation of wedge angle θ againstfor three Qλ=1cases.In each case,the upper limit of θ(bold lines)is constant due to the fixed Qλ=1while the lower limit of θ(thin curves) represents varied wedge angle at weak point W(θW) that depends on. For one-dimensional and steady problem, the final thermodynamic state of the detonation is only dependent on the chemical heat release and specific heat ratio for case.Thus,for specific gases with fixed δ and γ(polytropic gases),the upper limit depends on Qλ=1,while the lower limit depends on Qmax(Eq. (17)). As a result, the constant Qλ=1leads to the constant upper limit, and the varied Qmax(due to the pathological detonation behavior) leads to the different generalized CJ state and subsequently lower limit. The results in Fig. 10 reveal that smaller Qλ=1or largercontributes to wider standing window of ODW. The effect of Qλ=1on the standing window in present study is the same as that by Pratt et al.,8because Qλ=1represents the total heat release when reactions have completed. On the other hand,the effect ofon the standing window suggests that strengthening of endothermic process in reactions is in favor of widening of standing window.

Fig.11 displays the variation of MaPand MaCJwithfor the case of Qλ=1=50RT0. The difference between MaPand MaCJalways exists as long as＞1 and becomes apparent with the increase of,which explains the pathological detonation (MaP＞MaCJ) due to endothermic effect. Note that along with,MaCJis constant for fixed Qλ=1while MaPvaries due to its dependence on Qmax(see Fig.9).Similar to that in Section 3.3, we propose the heat equivalent parameters,/MaP, to collapse three Qλ=1used in present study into equivalent one. Fig. 12 shows the quadratic fittings between/MaPand Δθ. It can be seen from Fig. 12 that/MaPshows the good correlation with Δθ (R2=0.9125), suggesting that the enhancement of endothermic effect always broadens the standing window of oblique detonation regardless of variation of Qλ=1.

Fig. 11 Mach numbers of CJ detonation and generalized CJ(point P) detonation with different (Qλ=1=50RT0).

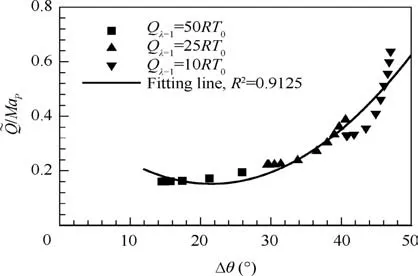
Fig. 12 Standing window Δθ for equivalent heat parameters/MaP.

4. Conclusions

The present study discusses the effects of thermodynamics,Mach number and heat release of hypersonic incoming flow on the standing behavior of oblique detonation that is formed by impacting of the incoming flow on a wedge with an angle of θ.A single-step,irreversible and exothermic reaction with mole variation is adopted to character the thermodynamic and flow effects, while the two-step, irreversible reactions with endothermic step are employed to describe the heat release effect. Both reaction with mole decrement and reactions with exothermic step display the pathological detonation behavior in which the classical CJ state never happens. This allows us to modify the lower limit of the standing window of ODW in the steady state analysis of detonation polar.The main conclusions include:

(1) Either weak solution or strong solution of the pathological detonation is possible as the lower limit of the standing window of ODW, which depends on the rare boundary condition (wedge wall profile). The choice of weak solution as a lower limit of standing window can give wider window range and thus smaller wedge angle is suggested. This provides larger space and reduces pressure loss in designing the combustor of ODW engine.

(2) Three equivalent parameters,Ma0/MaPand/MaP,are proposed to quantitatively describe the effects of thermodynamics,flow and heat on the standing window of ODW,respectively.The good correlations among the parameters and standing window imply that the decrease of specific heat ratio, the increase of overdrive degree of detonation and the enhancement of endothermic level result in the broadening of the standing window of ODW, for either pathological state or CJ state of detonations.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (No. 11872213), the Open Fund of Key Laboratory of Transient Physics,NJUST(No.6142604180205)and the Opening Project of State Key Laboratory of Explosion Science and Technology (Beijing Institute of Technology)(No.KFJJ17-11M).