A low-diffusion robust flux splitting scheme towards wide-ranging Mach number flows

Shushng CHEN, Fangji CAI, Xinghao XIANG, Zhnghong GAO,Chao YAN

a School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

b AVIC The First Aircraft Institute, Xi’an 710089, China

c China Academy of Launch Vehicle Technology, Beijing 100076, China

d State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China

e School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

KEYWORDS Computational Fluid Dynamics (CFD);Flux splitting;Accuracy;Robustness;Wide-ranging Mach number

Abstract This paper develops a low-diffusion robust flux splitting scheme termed TVAP to achieve the simulation of wide-ranging Mach number flows.Based on Toro-Va´zquez splitting approach,the new scheme splits inviscid flux into convective system and pressure system.This method introduces Mach number splitting function and numerical sound speed to evaluate advection system. Meanwhile, pressure diffusion term, pressure momentum flux, interface pressure and interface velocity are constructed to measure pressure system. Then, typical test problems are utilized to systematically assess the robustness and accuracy of the resulting scheme.Matrix stability analysis and a series of numerical cases, such as double shear-layer problem and hypersonic viscous flow over blunt cone,demonstrate that TVAP scheme achieves excellent low diffusion,shock stability,contact discontinuity and low-speed resolution, and is potentially a good candidate for wide-ranging Mach number flows.

1. Introduction

Nowadays, Computational Fluid Dynamics (CFD) has broad applications in analysis and design of aeronautics and astronautics.1,2With the comprehensive advantages of efficiency and accuracy, upwind schemes have been widely applied in simulating compressible flows. However, many investigations have demonstrated that upwind schemes face some difficulties in wide-ranging Mach number flow, such as low-speed deteriorated accuracy3-7and shock anomaly.8,9Thus, it is very encouraging to further develop advanced numerical solutions with high levels of robustness and accuracy.

In 1959, Godunov10proposed a first-order Godunov scheme based on Riemann exact solution. Although it has large computation amount and serious numerical dissipation,the idea of Godunov opens a new path for the development of numerical schemes. Many researchers have successively developed a series of the approximate Riemann solvers along this path, which effectively reduced computation amount and improved the calculation efficiency, and greatly promoted the development of CFD.Among these approximate solutions,the most widely used methods are Flux Difference Splitting(FDS), Flux Vector Splitting (FVS) and hybrid flux difference methods (e.g. AUSM-family schemes).

In 1981,on the basis of Godunov method,Roe11linearized Riemann problem by constructing Roe-average matrix and then proposed the celebrated Roe scheme. Its idea of approximate Riemann solution led the upsurge research of FDS method. According to the wave structure of Euler system,FDS methods can be divided into complete approximate Riemann solvers and incomplete approximate Riemann solvers.12The complete approximate Riemann solvers have a consistent wave structure with the exact Riemann solver, including two nonlinear waves(expansion wave,shock wave)and one contact discontinuity.The celebrated Roe scheme belongs to complete approximate Riemann solvers, and other complete solvers include Harten-Lax-van Leer scheme with Contact restoration(HLLC scheme)13Osher scheme14, etc. Among them, HLLC scheme is an approximate Riemann solver based on wave system simulation proposed by Toro et al.13All these methods have been widely applied due to excellent performances in simulating linear waves(e.g.viscous boundary layers,contact discontinuities)and steady strong nonlinear waves.However,the catastrophic defect is that the complete approximate Riemann solvers are prone to shock anomalies or carbuncle phenomena at high speeds.8,9In contrast,the incomplete approximate Riemann solvers ignore linear waves and have a relatively simple wave structure.Therefore, they lack contact discontinuity and shear wave capture capability, and have large dissipation and poor viscous resolution. But this kind of method has ability of capturing strong nonlinear waves(such as shock waves)with small calculation amount and high efficiency.It can also avoid carbuncle phenomenon effectively for it has good shock wave stability. At present, the incomplete Riemann solvers include two-wave approximate Riemann solver and one-wave approximate Riemann solver. For example, Rusanov15proposed the simplest one-wave approximate Riemann solver (Rusanov scheme) in 1961 and Harten et al.16developed the two-wave approximate Riemann solver(HLL scheme)in 1983.

In 1952, Courant et al.17developed an explicit first-order FVS scheme. In 1981, Steger and Warming18split the inviscid flux by the sign of the eigenvalues and proposed the first practical FVS scheme, named Steger-Warming scheme. Then,through theoretical analysis, van Leer19found that Steger-Warming scheme caused a discontinuity in the eigenvalue variation area(such as stagnation point or sonic point),and errors occurred in the calculation. To overcome this shortcoming,van Leer19proposed a new splitting method, van Leer’s FVS scheme, based on seven principles. FVS methods are simple in structure, and their properties are similar to those of the incomplete approximate Riemann solvers. They have strong nonlinear wave capturing capability, high computational efficiency and shock stability. Nevertheless, FVS methods cannot accurately capture linear contact discontinuities and shear waves, and have the poor viscous resolution.

Subsequently, the hybrid methods which combine the merits of FDS and FVS methods have been studied vastly. The idea of hybrid flux splitting methods is to treat acoustic waves and convective waves as different physical process and therefore divide inviscid flux into convective and pressure systems separately. The main splitting approaches include Liou-Steffen splitting,20,21Zha-Bilgen splitting22,23and Toro-Va´zquez splitting.24,25In 1993, Liou and Steffen20proposed AUSM(Advection Upstream Splitting Method).It was subsequently improved and developed into AUSM+scheme21in 1996.AUSM+scheme has been widely used for its high nonlinear and linear wave resolution, small numerical dissipation,no entropy correction, and scalar positivity. However,AUSM+is prone to non-physical pressure oscillations near strong shock waves and low-speed regions near the wall.26To overcome this shortcoming, Kim et al.26,27introduced the pressure-based weight function, defined the new interface numerical sound speed,and successively developed AUSMPW and AUSMPW+schemes. On the other hand, Convective Upwind Split Pressure scheme with the total Energy(E-CUSP scheme)22,23and Toro-Va´zquez (TV) scheme24,25based on Zha-Bilgen splitting and Toro-Va´zquez splitting have been successfully applied in 1D/2D flows, whereas the performances on complex flows remain to be verified. In addition,Sun and Takayama28used Zha-Bilgen splitting approach to propose a special flux splitting method based on the artificial wave speeds, namely Artificially Upstream Flux vector Splitting (AUFS) scheme. The scheme is simple, and robust to shock waves,which can accurately solve contact discontinuities, while it introduces excessive dissipation on shear waves,which easily smears boundary layer.29

However, numerical schemes mentioned above often encounter two problems,difficult convergence and deteriorated accuracy,3,30when low-speed flow is simulated. In order to solve these problems,a research boom in preconditioning techniques31-34has been started since the middle of 1990. Meanwhile, based on asymptotic analysis,4a series of new numerical flux schemes (AUSM+UP3, LDFSS,35SLAU,36SLAU2,37EC-RoeM,38All-Speed Roe,5LMRoe,6LDRoe,7etc.) are subsequently obtained, which are suitable for lowspeed simulation. Nevertheless, such methods still face some flaws, which reduce the overall computational efficiency and accuracy.36For instance, preconditioning techniques suffer from global cut-off problem,34sacrifice of time accuracy, etc.AUSM+UP, SLAU, SLAU2 and other schemes may suffer from shock anomalies in hypersonic flow simulation,39,40especially in large mesh aspect ratio.40The low-speed improved Roe schemes(All-Speed Roe,LMRoe,LDRoe,etc.)still encounter carbuncle phenomenon in high Mach number regimes.

Thus, it is very essential to further develop numerical schemes and improve the reliability in wide-speed flow.In this paper,we propose a new flux splitting scheme which is suitable for simulating wide-ranging Mach number flows. Considering that Toro-Va´zquez splitting has good mathematical and physical properties, the new scheme constructs advection flux and pressure flux separately by following this splitting. The resulting scheme does not require problem-dependent parameters and has high accuracy and robustness, denoted as TVAP scheme. Numerical benchmark problems and complex flow simulations are tested to push out its effectiveness in wideranging Mach number flows.

The present paper is organized as follows.A brief introduction on Navier-Stokes equations and Toro-Va´zquez splitting is given in Section 2. In Section 3, the TVAP scheme is introduced and the characteristics of the scheme are analyzed. In Section 4, the proposed scheme is assessed in terms of robustness and accuracy. Section 5 carries out a series of numerical cases. Finally, conclusions are drawn in Section 6.

2. Navier-Stokes equations and Toro-Va´zquez splitting

2.1. Navier-Stokes equations

Consider the compressible Navier-Stokes equations in Cartesian coordinates:

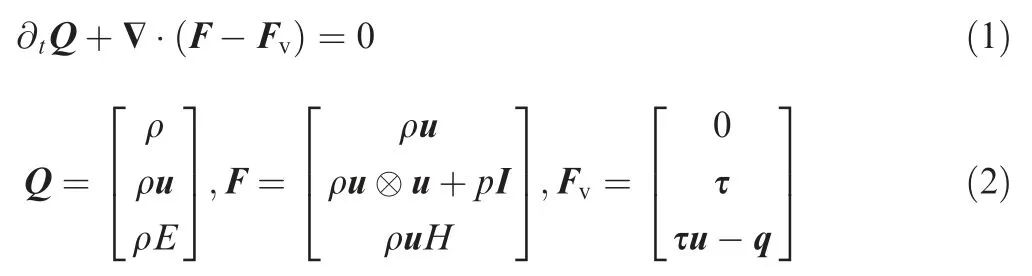
with Hamilton operator ∇, dyadic product ⊗, identity matrix I, conservative state vector Q, inviscid flux vector F, and viscous flux vector Fv. ρ,p and u= [u，v，w]Tare density, pressure and velocity respectively. To close the equations, the perfect gas law with the specific heat ratio γ=1.4 is employed

with temperature T and gas constant R. Under Stokes’hypothesis, the shear stress tensor and heat flux are given as

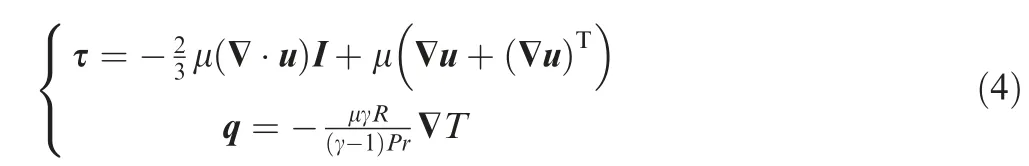
with Prandtl number Pr, and viscosity coefficient μ. Then, the sound speed a， specific total energy E and enthalpy H are defined as

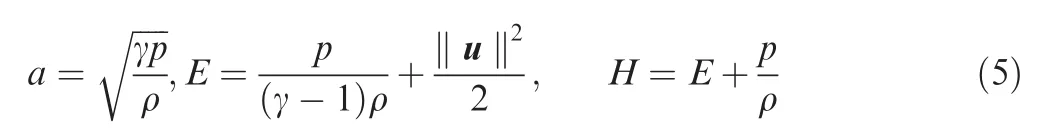
In the present study,all numerical simulations are carried out on multi-block structured grids. The central difference scheme(e.g.second-order or fourth-order)is applied to calculate the viscous flux Fv.As for the inviscid flux F，the popular spatial discretization generally consists of two procedures: firstly, the primitive variables at each cell interface are interpolated by reconstruction methods(e.g.first-order,second-order MUSCL approach41);secondly,the inviscid flux is evaluated by Riemann solvers (e.g. Roe,11AUSM+,21SLAU,36TV24,25) using the reconstructed primitive variables. The time-integration technique uses either the explicit 3th TVD Runge-Kutta scheme or the implicit LU-SGS (Lower-Upper Symmetric Gauss-Seidel)approach.42The current work concentrates on the approximate Riemann solver for the inviscid flux.

2.2. Toro-Va´zquez splitting

On a dimension-by-dimension basis,12it usually employs the quasi-one-dimensional Riemann solver to evaluate numerical flux for solving multidimensional hyperbolic problems. Thus,without loss of generality, we consider the inviscid flux in one-dimensional Cartesian coordinates. By dropping the viscous flux Fvof Eq. (1), one-dimensional Euler equations can be expressed as

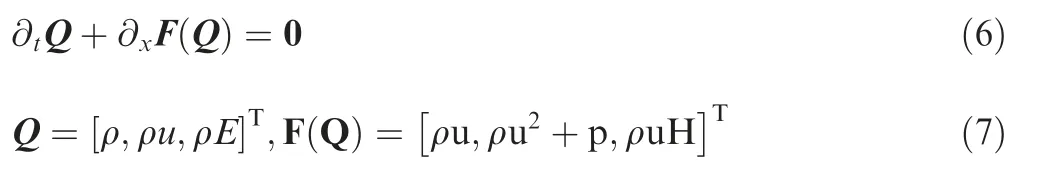
This Euler system is numerically discretized in conservation form

The subscripts ‘‘L” and ‘‘R” represent the left and right states calculated by reconstruction methods respectively.Assumed as a Lipschitz continuous function,Fi+1/2should satisfy the consistency condition:

Following the flux vector splitting methods, the inviscid flux F(Q ) can be divided into advection and pressure systems:

Then, the numerical flux Fi+1/2is expressed as the sum of the numerical advection flux Ai+1/2and the numerical pressure flux Pi+1/2:

Under the framework of Toro-Va´zquez splitting approach,24,25the advection and pressure systems are given as

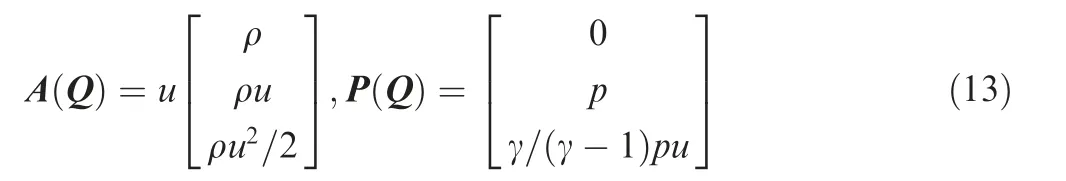
The advection flux A(Q )involves no pressure term, and all pressure terms are included in the pressure flux P(Q ). The advection flux A(Q ) is further expressed as

A(Q ) can be expressed as the production of H(Q ) (mass,momentum and kinetic energy) and convective speed u24,25.The Jacobian matrix of advection flux A(Q ) is acquired as

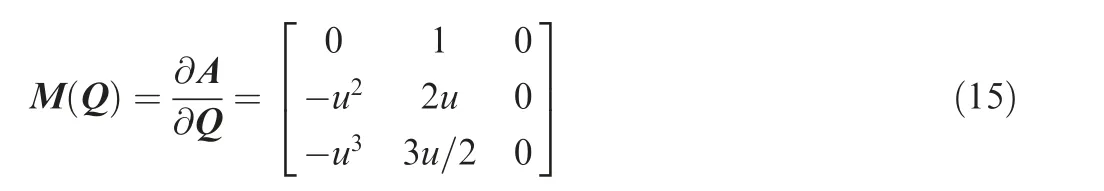
with three eigenvalues

Since there is no complete set of linearly independent eigenvectors, the advection system A(Q ) is weakly hyperbolic. For the pressure flux P (Q ), its Jacobian matrix is as follows:

with three different and real eigenvalues

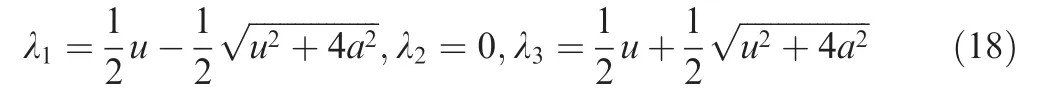
Obviously, the pressure system P(Q ) is always subsonic.

3. A new low-diffusion robust flux splitting scheme

Toro et al.24,25have proposed TV scheme built on the framework of treating advection and pressure systems separately.However, many typical symptoms of TV scheme have been observed, especially in hypersonic and very low speeds. Thus,to effectively expand the application range and improve the reliability, this paper comprehensively reconstructs the advection and pressure systems, accomplishing a low-diffusion robust scheme towards wide-speed flows. The new scheme is termed TVAP where the suffixes‘‘A”and‘‘P”stand for advection flux and pressure flux respectively.

3.1. Evaluation of advection system

The advection system A(Q )consists of the passive scalar quantities H(Q ) and convective speed u. The underlying idea is to express convective speed u as the product of Mach number M and sound speed a, i.e. u=M.a. Then, advection flux A(Q ) can be recast as

The important feature is that the propagation of H (Q )depends on Mach number M. Considering that the advection system is weakly hyperbolic, the numerical advection flux Ai+1/2can be established as

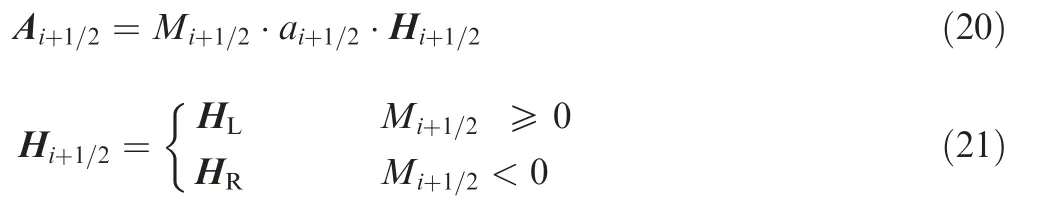
with the numerical sound ai+1/2and the interface Mach number Mi+1/2. The sign of Mi+1/2determines that Hi+1/2takes either the left or right state.

(1) Numerical sound speed

Since the interface numerical sound speed ai+1/2plays a crucial role in the resolution of physical discontinuities,37the reasonable design of ai+1/2is indispensable. Firstly, ai+1/2should effectively reflect the contribution of sound speed in each side(aLor aR).Secondly,it should take into account the largest signal velocity SRand the smallest signal velocity SLof Euler system using the format of HLLC scheme13

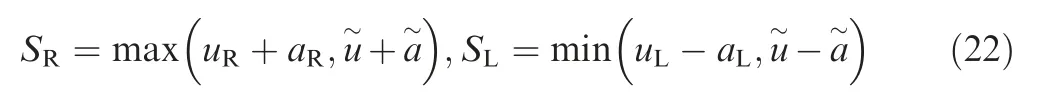
The superscript tilde ‘‘～” stands for Roe average. Finally,based on density weighted average, a new numerical sound speed can be devised via incorporating the left and right density values into Eq. (22)

The definition can satisfy entropy condition, remove unphysical expansion shock and have strong shock robustness against carbuncle phenomenon.

(2) Interface Mach number

The interface Mach number Mi+1/2involves the contributions from both the left and right Mach numbers.20,21Then,Mi+1/2is the combination of two individual components

It can represent two opposite waves travelling and interacting toward the interface. Following van Leer method,19the Mach number splitting function is given as

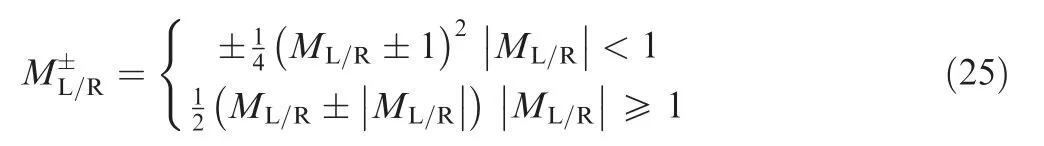
in which

3.2. Evaluation of pressure system

The pressure system P(Q )is subsonic with the structure of Riemann solution.The basic idea in evaluating pressure system is to adopt the non-dissipative central term and numerical dissipation term. The numerical pressure flux can be written as

with pressure diffusion term δpm,pressure formula ps,interface pressure p*and interface velocity u*.The current objective is to obtain the expression of Pi+1/2, while making TVAP scheme more robust and simpler.

(1) Pressure formula with low Mach number feature for momentum flux

Here, θL/Ris the pressure splitting function using trigonometric function, which is defined as

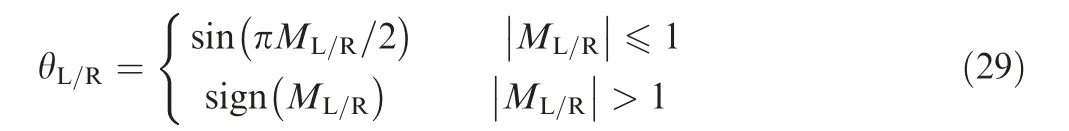
with the shock sensor ki.This sensor is used to recognize compressible sonic points across the cell interface, thereby removing possible small disturbances near the shock waves caused by the scaling function.

(2) Pressure diffusion term for mass flux

On the one hand,many literatures3,27have observed that it is easy to produce numerical oscillations in low Mach number limit or numerical overshoots behind strong shock waves if there is no corresponding dissipative mechanism in the pressure field for mass flux. On the other hand, Liou43demonstrated that the pressure diffusion term in mass flux has an adverse effect in combating carbuncle instability. Considering these two aspects comprehensively,the pressure diffusion term δpmis only active in subsonic regimes to stabilize low-speed simulations. Combining with dimensional analysis, we introduce the pressure diffusion term δpminto mass flux

In line with the scaling function f(Eq.(30)),the factor 1-f only works in subsonic regimes and meantime takes zero near the possible shock waves.

(3) Interface pressure and velocity for energy flux

The interface pressure p*can be simply given via the sign of the interface Mach number Mi+1/2

Inspired by HLL algorithm,16the interface velocity u*is obtained as

The interface velocity u*is very robust and automatically equipped with upwind feature. For compatibility with mass flux, the pressure diffusion term δpmis introduced into energy flux.Based on the dimensional analysis,δpmshould be divided by the average density, which is consistent with u*. Then, the interface velocity u*can be expressed as

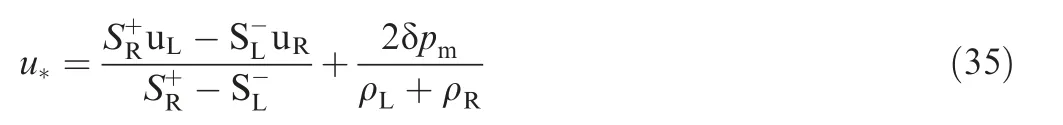
Finally, we accomplish the construction of the new TVAP scheme.

3.3. Evaluation to three dimensions

Then, the proposed TVAP flux is expressed in three dimensions

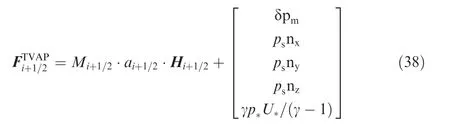
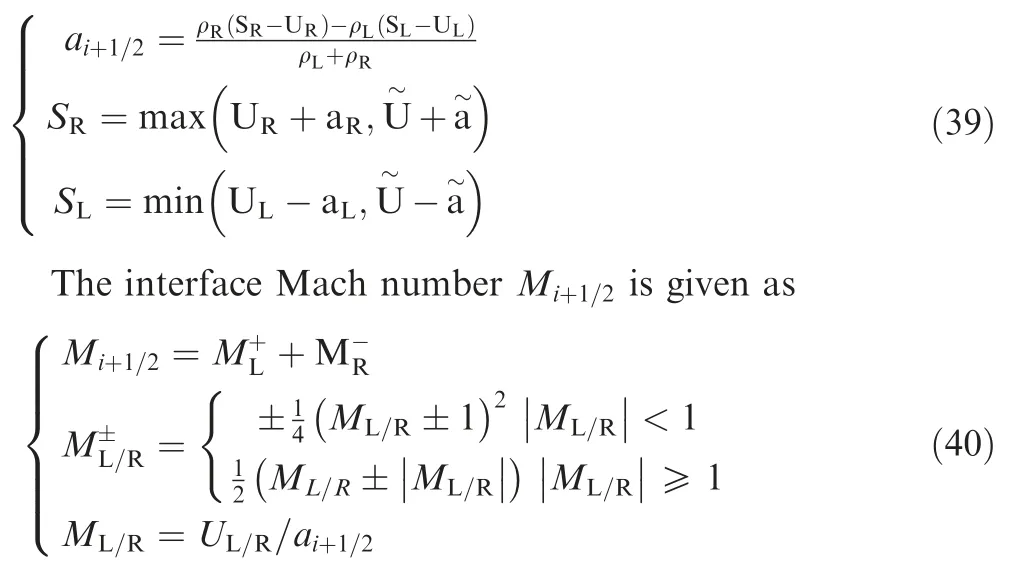
The sound speed ai+1/2is defined as

The pressure diffusion term δpm， pressure formula psand interface velocity U*are defined as

4. Assessment of proposed TVAP scheme

In this section, we launch systematical investigations into the features of TVAP scheme from four aspects. These aspects mainly include shock robustness, shear-layer resolution, lowspeed accuracy and other additional features.

4.1. Shock robustness

4.1.1. Steady normal shock by matrix stability analysis

Matrix stability analysis44is a powerful analytical tool that quantitatively reveals shock stability mechanism of numerical schemes. Many researchers44,45applied it to study carbuncle phenomenon. In this section, we will use the matrix stability analysis to demonstrate the stability behavior of the new flux splitting scheme.The corresponding computational conditions about the steady normal shock can be found in Refs.44,45

The eigenvalues of the stability matrixes of first-order Roe,AUSM+,TV and TVAP schemes under different Mach numbers are computed and their stability behaviors are analyzed.Fig. 1 shows the relationship between the maximum real part of eigenvalues and the Mach number computed by different schemes. And the distribution of the eigenvalues of the stability matrix calculated by different schemes are plotted in Fig.2.The calculation results of Roe scheme are completely consistent with the results of Refs.,44,45which can verify the current matrix stability analysis code.From these figures,we can draw the following conclusions:

(1) Roe and TV schemes have positive real part of eigenvalues over the threshold Mach number(Ma∞＞2),denoting that Roe and TV schemes are shock-unstable and suffer from carbuncle phenomenon.

(2) With the increase of upstream Mach number, the maximum real part of eigenvalues of Roe scheme continues to grow and it becomes more unstable. The maximum real part of eigenvalues of TV scheme gradually tends to a fixed value, but it is still positive.

(3) AUSM+scheme is quite special. Its maximum real part of eigenvalues is almost close to zero and maintains unchanged with the increase of upstream Mach number, indicating that AUSM+scheme is in a subtle critical stability state, and the robustness may be insufficient.

Fig. 1 Relationship between maximum real part of eigenvalues and Mach number.

(4) TVAP scheme has non-positive real part of eigenvalues.And the maximum real part of eigenvalues gradually approaches a negative fixed value as the Mach number increases, which demonstrates that TVAP is shockstable and can suppress shock anomalies effectively.

4.1.2. Hypersonic flow over 2D cylinder

Two-dimensional hypersonic inviscid flow over a cylinder at Ma∞=20 is presented to validate the shock-stable property of TVAP scheme. Many upwind schemes (e.g. Roe, TV) have encountered the well-known carbuncle phenomenon8,9,45in hypersonic blunt body computations. All simulations are performed with first-order accurate method and the implicit LUSGS approach42with CFL=5 as well as 20,000 time iterations. The computational mesh contains 239 (circumferential)×121 (wall normal) grid points.

Fig. 3 shows density contours (ρ/ρ∞) calculated by each scheme.Roe and TV schemes suffer from severe shock anomalies. Similar to AUSM+scheme, the flow field solved by TVAP scheme is clear and smooth without any shock anomaly under the current grid.

4.1.3. Odd-even decoupling

The odd-even decoupling problem8is considered to check whether numerical scheme may encounter shock instability.The initial shock is located at x=8, and the initial condition with a normal shock Ma∞=6 is given as

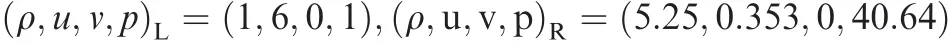
The generated mesh has 200( x )×40(y ) grid cells in[0，10]× [0，1 ] with a large aspect ratio. The centerline grid is disturbed by small numerical error ±10-4. All simulations are performed on first-order accuracy method.

Fig. 4 draws the density contours of the odd-even decoupling at t=1 s (Roe, TV) and t=5 s (AUSM+, TVAP).For this case, it easily triggers shock anomalies under the current mesh.As expected,Roe and TV yield the catastrophic carbuncle instability. AUSM+is prone to slight anomalous oscillations.The current TVAP scheme has good shock stability and reproduces the clear shock.

4.2. Shear layer

4.2.1. Stationary contact discontinuity

We consider stationary contact discontinuities to reveal the contact-resolving capability of TVAP.The length of shock tube is one with 50 grid cells.The initial conditions are specified as

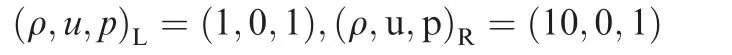
All simulations are conducted up to t=0.5 s with firstorder accuracy method. In Fig. 5, the density and pressure contributions computed by different schemes (HLL, TV and TVAP) are compared. We observe that HLL scheme smears contact wave,9whereas TVAP scheme is capable of resolving contact discontinuity exactly as well as the TV scheme.

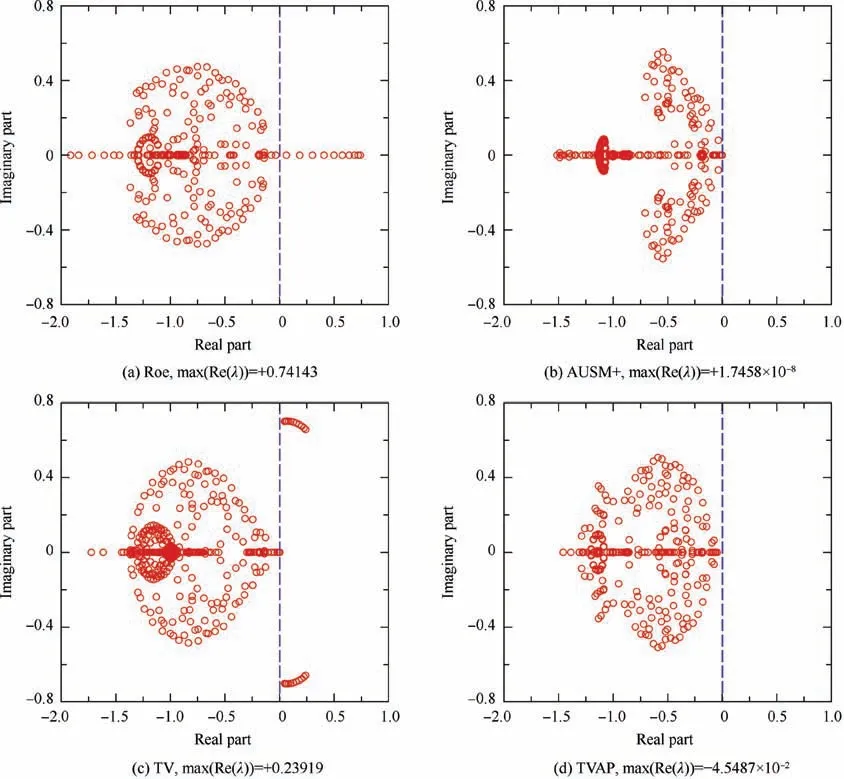
Fig. 2 Distribution of eigenvalues of stability matrix on complex plane (Ma∞=7).

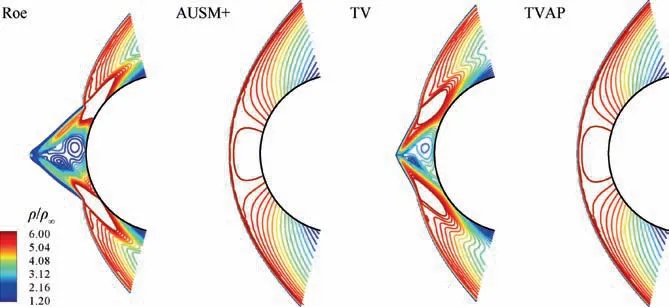
Fig. 3 Density contours of hypersonic inviscid flow over 2D cylinder.

4.2.2. Flat-plate laminar boundary layer

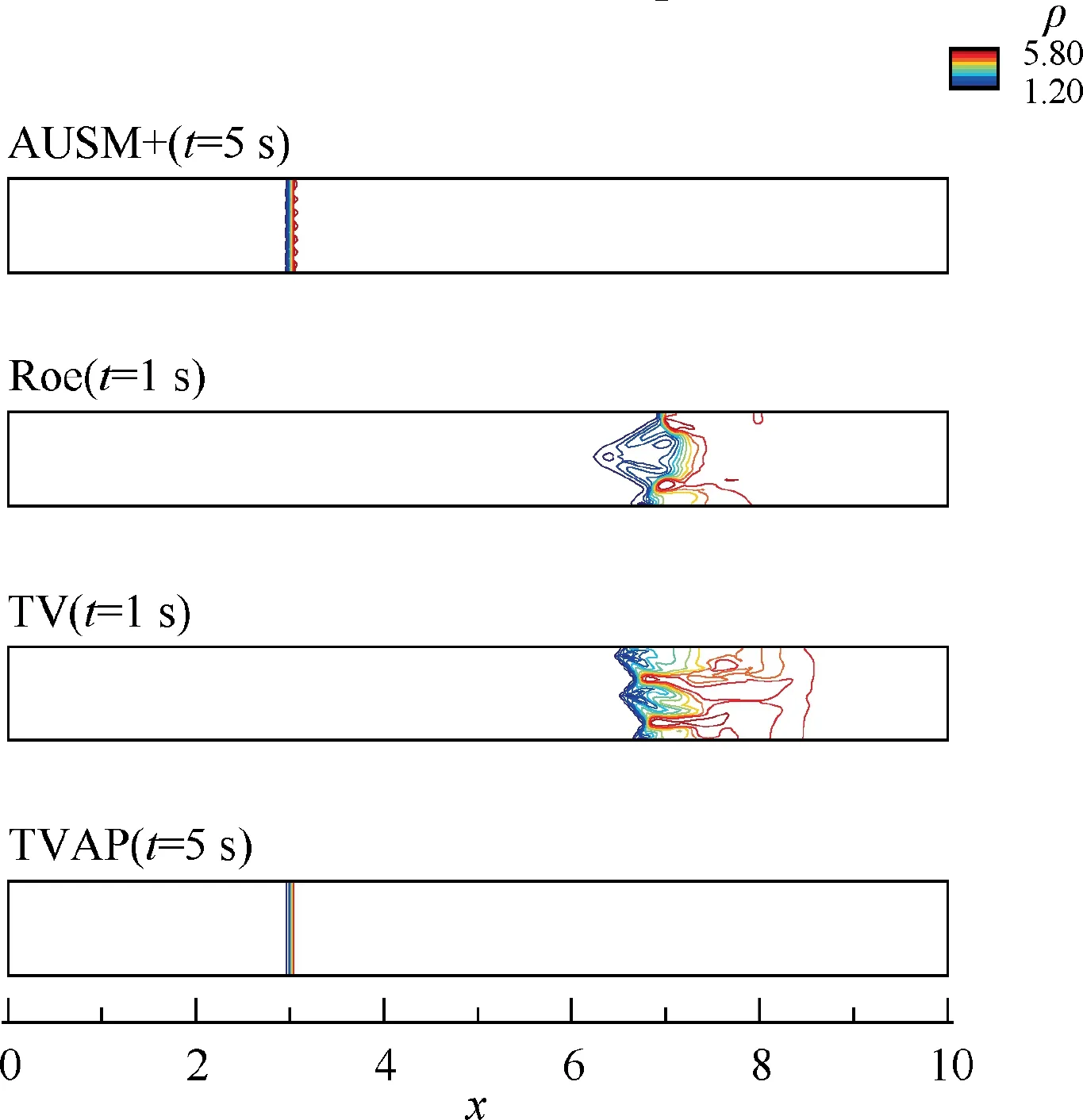
Fig. 4 Density contours of odd-even decoupling.

Fig. 5 Stationary contact discontinuity.

4.3. Low-speed accuracy

Fig. 6 Flat-plate boundary layer.

The ideal Euler equation satisfies that the pressure spatial variation (Ind(p )= (pmax-pmin)/pmax) is proportional to the square of Mach number at low Mach numbers.4However,typical upwind schemes(e.g.Roe and TV)have loss of accuracy at low speeds and the resulted pressure spatial variation is only proportional to Mach number4,36,37,38as a consequence of the excessive numerical viscosity. In contrast, the low Mach behavior of TVAP scheme fits well with the properties of the ideal Euler equation: the pressure spatial variation is proportional to the quadratic of Mach number and the numerical dissipation is more reasonable and controllable,which effectively avoid low-speed deteriorated accuracy and improve low-speed resolution. The inviscid low Mach number flows over a cylinder are presented to illustrate this behavior.

The calculation domain is Ω= [r0，r1]× [φ0，φ1]=[0.5，20]× [0，2π], where r0is the cylinder radius and r1is the outer boundary radius. The computational mesh uses an O-type topology with 301 (circumferential)×401 (wall normal) grid points. Farfield and slip boundary conditions are used for the outer boundary and wall respectively. All simulations are conducted up to 50,000 time iterations by first-order accurate method and the implicit LU-SGS approach with CFL=50. The freestream Mach number is Ma∞=0.001，0.01，0.1.

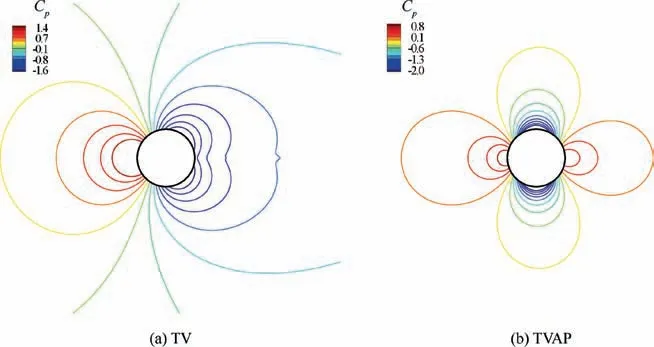
Fig. 7 Pressure isolines of inviscid flows over a cylinder (Ma∞=0.01).

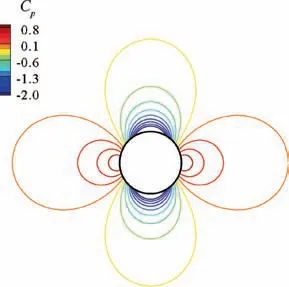
Fig. 8 Pressure isolines (Ma∞=0.01) by TVAP scheme on a finer mesh.

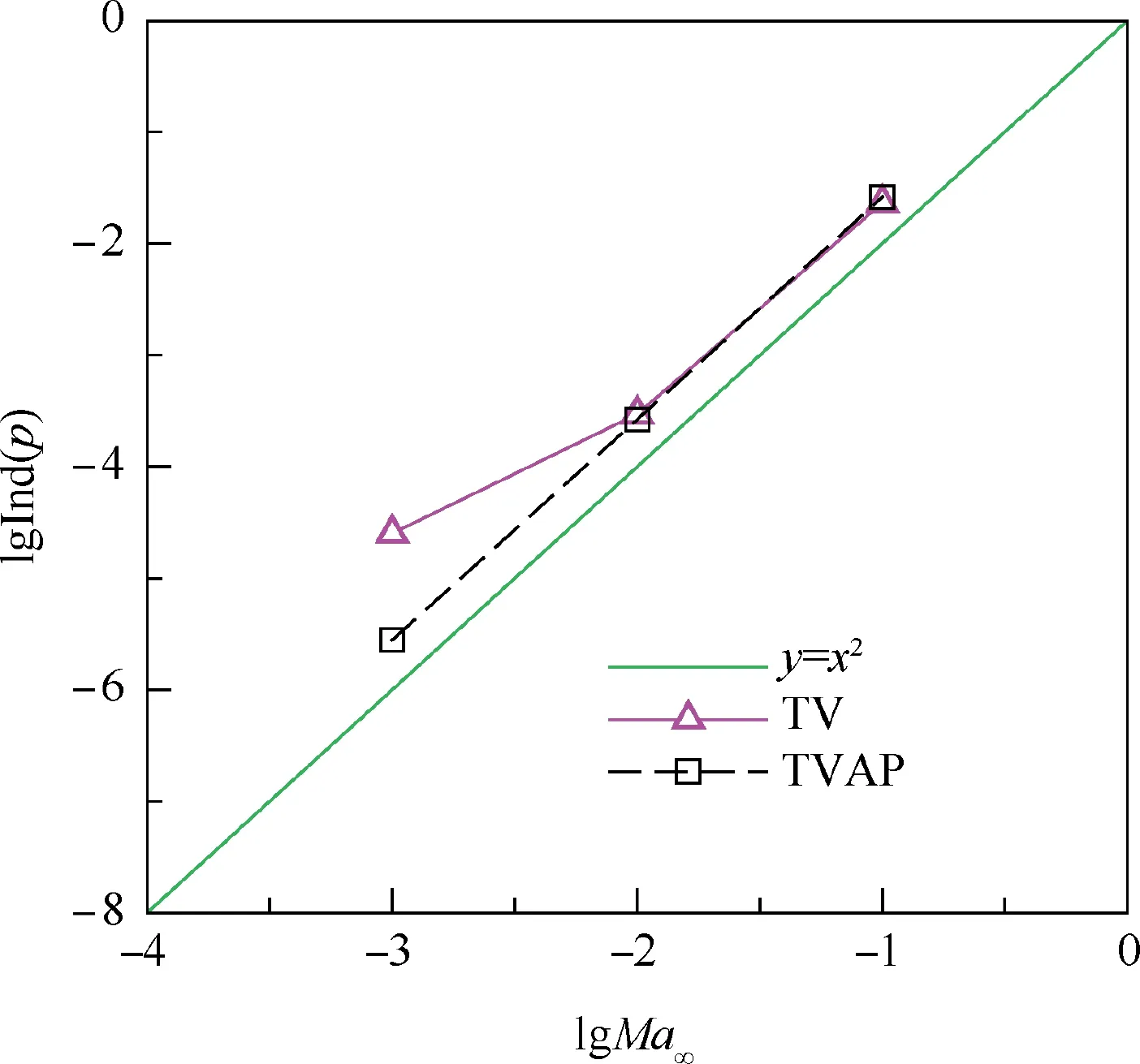
Fig. 9 Relationship between pressure spatial variation and Mach number.

4.4. Additional features

In what follows, three shock tube problems are simulated to reveal the additional features of TVAP. Note that all cases are conducted with first-order reconstruction in space and the explicit 3th TVD Runge-Kutta scheme in time with CFL=0.4.

4.4.1. Sonic point problem

The density distributions calculated by each scheme at t=0.2 s are displayed in Fig. 11. It can be observed that the TVAP scheme does not generate non-physical oscillations and achieves good physical solution. Furthermore, TVAP scheme predicts a more rational and sharp distribution near the shock and rarefaction wave heads compared to Roe and TV schemes.

5. Numerical results

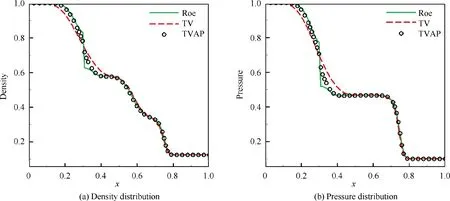
Fig. 10 Sonic point resolution.

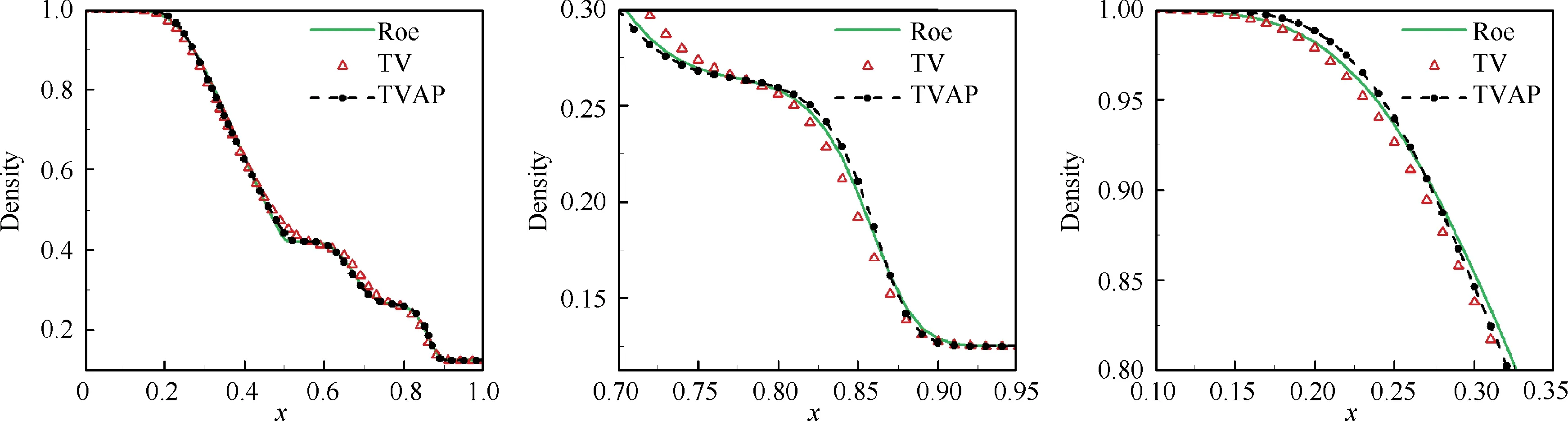
Fig. 11 Sod shock tube: density distributions.

Next, a series of practical applications across wide-ranging Mach numbers are conducted to highlight the effectiveness of TVAP scheme. These test cases include double shear-layer problem at Ma∞=0.01, transonic flow over RAE2822 airfoil at Ma∞=0.75 and hypersonic viscous flow over blunt cone at Ma∞=10.6. Unstructured grid is a good candidate to simulate complex flow situations. In fact, TVAP scheme can work with unstructured grid,but unstructured grid has more prominent problems than structured grid, especially in hypersonic heating prediction.47With this reason, the current study concentrates on the performance of numerical flux on structured grid. Undoubtedly, the extension towards unstructured grid is also worth further studying.

5.1. Low-speed double shear-layer problem

Double shear-layer problem is simulated to exhibit the performance of TVAP scheme in unsteady low Mach number flow.This test case involves shear layers and strong vertical structures. The setting of initial conditions and the detailed formulation about this problem are taken from Refs.,38,48,49making it a weakly compressible flow.The freestream Mach number is specified as Ma∞=0.01. The computational domain has 128×128 grid cells in [0，2π]× [0，2π]. The periodic boundary condition is used at four edges. All simulations are run to t=8.0 s by second-order accurate method and the explicit 3th TVD Runge-Kutta scheme with Δt=5×10-5s. The reference solution is performed on a very fine mesh with 512×512 grid cells using TVAP scheme. At this grid density,the influences of the flux scheme are negligible.48

Fig. 12 presents vorticity contours calculated by three schemes. Fig.13 plots the v velocity profile along x=π calculated by relevant schemes. Roe and AUSM+schemes have higher numerical dissipation and are more susceptible to contamination of vortex structures. On the contrary, TVAP and SLAU schemes have better resolution accuracy and predict sharper vortices. In addition, the resolution of the results obtained by TVAP scheme is slightly higher than that obtained by SLAU scheme.

5.2. Transonic flow over RAE2822 airfoil

Viscous turbulent flows over RAE2822 airfoil at transonic regime are usually employed for turbulence model validation.Cook et al.50have experimentally investigated RAE2822 airfoil. This case generates a compression shock interacting with boundary layer and a small recirculation separation bubble behind the shock. The corresponding freestream conditions are set as follows: Ma∞=0.75, angle of attack α=2.81°, Re∞=6.2×106and adiabatic wall. The mesh has 349 (circumferential)×151 (wall normal) grid points and the first gird distance in boundary layer is 3×10-6m. Such mesh ensures sufficient resolution for predicting the flow physics.All computations are run up to 50,000 time iterations by Roe and TVAP schemes using second-order MUSCL approach with minmod limiter,41Shear Stress Transport (SST) turbulence model51and LU-SGS approach with CFL=15.

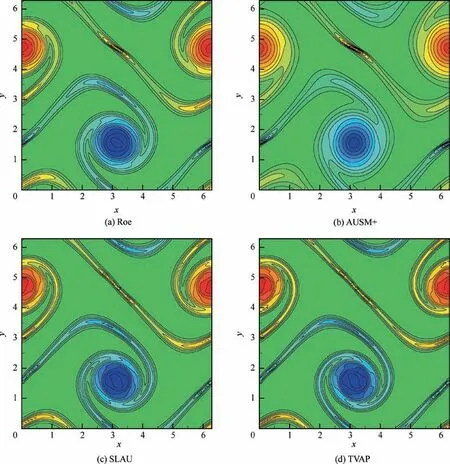
Fig. 12 Double shear-layer problem: vorticity contours from -4.75 to 4.75.

Fig. 13 Double shear-layer problem:vvelocity profiles alongx=π.

As shown in Fig. 14, TVAP scheme obtains a smooth and clear flow field distribution.Fig.15 shows pressure coefficients of airfoil surface with chord length c=1 m. As can be seen,TVAP scheme characterized the accurate and stable shock position, and pressure coefficients are in good agreement with the experimental ones.50It proves that TVAP scheme, combined with turbulence model, is suitable to simulate transonic flows.

5.3. Hypersonic viscous flow over 3D blunt cone

Hypersonic laminar flow over blunt cone in three dimensions is conducted to verify the superiority of TVAP scheme in terms of hypersonic heating prediction. In fact, using existing schemes to achieve satisfactory heating prediction at the head of blunt cone remains a huge challenge.47

The test conditions taken from Cleary’s experiment52are set as:Ma∞=10.6,freestream temperature T∞=47.3 K,wall temperature Tw=294.44 K,α=0°and Re∞=3.937×106/m.For this blunt cone,the radius is r=27.94 mm and the length is l=447 mm. As shown in Fig. 16, we generated the multiblock structural mesh with the total grid cells number about 9.93×105. To match the corresponding physical phenomena(the strong nonlinear temperature distribution in boundary layer and large variable jumps at shock wave), the grid points are clustered to shock wave and meantime the minimum mesh size near the wall is 1.5×10-3mm with the cell Reynolds number Recell=5.9. The second-order central difference scheme is used to discretize the viscous flux, and the secondorder MUSCL approach (minmod limiter) is applied to the inviscid flux. The simulations are run up to 50,000 time iterations by the implicit LU-SGS approach with CFL=2.5 to assure the computational convergence. Here, we compare TVAP with Roe, AUSM+and SLAU.

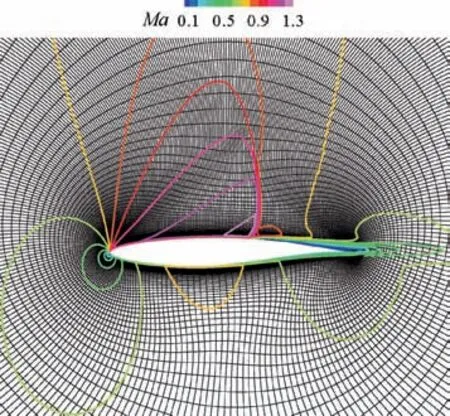
Fig.14 Equally spaced Mach number contour levels from 0.1 to 1.3 for TVAP.

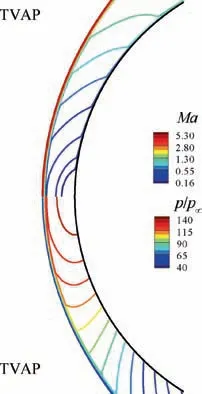
Fig.17 Mach number and pressure isolines on symmetry plane.

Fig. 15 Surface pressure coefficient over chord length.

Fig. 16 Partial head mesh.

Fig. 17 plots Mach number and pressure isolines on symmetry plane of the head.TVAP is robust against shock anomalies and averts many undesirable symptoms.It achieves a clear and smooth Mach number and pressure distribution.

Further, Fig. 18 displays the distributions of the surface heating value (Q) at the head of blunt cone. Some important conclusions are drawn: (A) Roe scheme without the entropy fix suffers from carbuncle instability,and gives the very wrong heating distributions. (B) AUSM+, SLAU, and TVAP give a smooth heat flow distribution,and the stagnation point values agree well with the experimental values (215775 W/m2).52(C)AUSM+easily yields numerical wiggle near the wall and numerical overshoots behind strong shock waves. The peak heating value of AUSM+ (198198W/m2) and SLAU(195358 W/m2)are not located at stagnation point,and meantime the heating distributions are asymmetry. (D) TVAP attains the smooth and symmetry heating distributions, and the peak heating value(199850 W/m2)is located at stagnation point. This illustrates that TVAP scheme acquires the favorable accuracy and reliability for hypersonic heating prediction.

6. Conclusions and outlook

The paper has developed a low-diffusion robust scheme termed TVAP, built on Toro-Va´zquez splitting approach. It constructs advection and pressure systems respectively to achieve accuracy and robustness for wide-ranging Mach number.This scheme also avoids empirical problem-dependent parameters and has high resolution. Matrix stability analysis, hypersonic inviscid flow over a cylinder and odd-even decoupling problem confirm that TVAP has high-level robustness against shock instability. Low Mach number flows over a cylinder and double shear-layer problem display that TVAP reduces numerical dissipation and recovers the proper accuracy at low speeds.RAE2822 airfoil demonstrates that TVAP can work well with turbulence model at transonic regime.Hypersonic viscous flow over 3D blunt cone indicates a potential application of the proposed scheme to hypersonic heating prediction. These results exhibit that TVAP is attractive across wide-ranging Mach number flows.

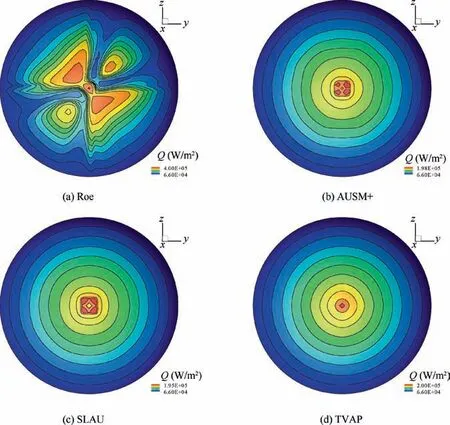
Fig. 18 Surface heating distributions at the head of blunt cone.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was supported by the Space Science and Technology Fund Project of China (No. 2020-HT-XG-14). The authors are grateful to the anonymous reviwers for the constructive comments.