A multi-stage regulation strategy of space manipulators with a free-swinging joint failure

Gang CHEN, Yingzhuo FU, Qingxuan JIA, Bonan YUAN, Dan LIU

School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China

KEYWORDS Free-swinging joint failure;Fuzzy entropy;Multi-stage regulation strategy;Regulation ability;Space manipulator

Abstract To ensure tasks can be completed after a free-swinging joint failure occurs,a multi-stage regulation strategy of space manipulators is proposed.Considering all terms of the dynamics equation, an evaluation model of the regulation ability (EMRA) of active joints over the fault joint is established based on the fuzzy entropy. And then a multi-stage regulation strategy based on the EMRA is designed to regulate the fault joint. The strategy divides the regulation process into several stages, and select a certain active joint to regulative the fault joint in every stage. With this multi-stage regulation strategy, the fault joint can be regulated to the desired angle without huge torque on regulative joints. The simulation is carried out with a 7-DOF space manipulator, verifying the correctness and effectiveness of the multi-stage regulation strategy. The strategy has three advantages:Coriolis and centrifugal terms are both considered for the first time in selecting the regulative joint, making the selection result more in line with the actual regulation process; The influence of the model uncertainty is eliminated in establishing the EMRA, making the evaluation of regulative ability more precise;The fault joint is successfully regulated to the desired angle without huge torque on regulative joints.

1. Introduction

Space manipulators are usually used to assist or replace the astronaut to perform space missions, such as spacecraft docking,satellite release,space station maintenance and assembly.1However, due to the burdensome tasks and harsh space environment, a joint failure is prone to happen, especially the free-swinging joint failure.2,3When this kind of failure occurs,the fault joint cannot provide any motion and torque as expected due to its swinging state,easily leading to a task failure.3To ensure that tasks can be completed after the freeswinging joint failure occurs, a failure treatment strategy for space manipulators needs to be studied.

Some scholars have studied on the failure treatment strategy for space manipulators with a free-swinging joint failure(also called an underactuated space manipulator). English and Maciejewski4determined the desired angle of the fault joint by taking the postfailure workspace as the optimization objective, and regulated the fault joint to the desired angle through a speed control method. Maciel et al.5established an optimization criterion based on the local coupling index,and designed a robust controller to regulate the freeswinging joint via the active joint, which operates normally.Based on the dynamics coupling relationship between the fault and active joint (DCRFAJ), Chen et al.6regulate the fault joint to the desired angle with a PD control method. From above researches, the failure treatment strategy for a freeswinging joint failure is to use active joints to regulate the fault joint towards a desired angle based on the DCRFAJ.

According to the dynamics coupling characteristic of the manipulator, the regulation ability of each active joint over the fault joint is different,which is embodied on efficiency difference of the motion transmission.7If an active joint is randomly selected as the regulative joint, it may lead to a low regulation ability and high energy consumption. Therefore, it is necessary to select an appropriate active joint as the regulative joint.

To solve this problem,Bergerman et al.8established a local coupling index, which can provide a gist for selecting the regulative joint. The local coupling index reflects the regulation ability of each active joint over the fault joint. However, the local coupling index changes with the manipulator configuration, and we cannot decide which active joint has greater coupling with the fault joint in the whole joint space. Therefore,we should pay more attention to the coupling index in a global sense,to measure the dynamic coupling within the entire workspace of manipulators. In this case, a global coupling index is proposed.9,10Through analyzing the joint coupling relationship at all manipulator configurations, the global coupling index evaluates the regulation ability of each active joint over the fault joint in the whole workspace, and it can be also used to select the regulative joint.

The local coupling index and global coupling index are both constructed with the inertia matrix of the manipulator dynamics model, and they describe the coupling degree between the joints in the static state of the manipulator.However, the manipulator is in motion during the regulation process, and from the dynamics model we can see that it also contains nonlinear terms,i.e.,Coriolis and centrifugal terms.11With the increase of the motion velocity, the proportion of nonlinear terms increases,which obviously affects the coupling degree between the fault joint and active joint. If the local or global coupling index is constructed only with inertia matrix,the selection of the regulative joint result is unreliable. Therefore,it is necessary to establish a new evaluation model of the regulation ability (EMRA) through taking Coriolis and centrifugal terms into account.

In the establishment of the new evaluation model, we regard the inertia matrix, Coriolis and centrifugal terms as evaluation information of each active joint. Through varying the space manipulator configuration, sets of evaluation information will be generated based on these terms.The evaluation information reflects the regulation ability of active joints from different manipulator configurations. To comprehensively evaluate the regulation ability of active joints,the entropy theory is adopted to deal with these sets of evaluation information. The entropy theory usually includes approximate entropy,12maximum entropy,13sample entropy,14fuzzy entropy,15etc. Due to measurement error and unmodeled dynamics existing in the design and use of the manipulator,there are some uncertainties in the dynamics model,16adding fuzziness to these set of evaluation information. Considering that the fuzzy entropy can eliminate the fuzziness to make a stability evaluation,17we will use it to establish the EMRA.

After selecting the regulative joint, a regulative strategy should be designed to regulate the fault joint with the DCRFAJ. Shin and Lee18proposed a feedback linearizing decoupling dynamic control scheme to obtain a desired trajectory of the free-swinging joint without singularity. He et al.19proposed a virtual model lead control method to make the free-swinging joint move along the desired trajectory for the underactuated redundant manipulator. However, Ref. [20,21]have proved that for an underactuated manipulator without gravity, the free-swinging joint and regulative joint cannot be stabilized at a certain angle simultaneously via a smooth control law on the regulative joint. In this case, a discontinuous control law should be designed for the underactuated space manipulator when the free-swinging joint reaches nearby the desired angle. In addition, above researches have ignored the regulative ability of the active joint during the manipulator motion.22When the local coupling index tends to be zero, the manipulator is located nearby the dynamic singular configuration. At this moment, the current regulative joint is unable to regulate the fault joint, leading to an infinity for its torque.So the regulative joint has to be transformed into a new active joint,which can regulative the fault joint without a huge torque on itself. Therefore, the regulation progress should be divided into several stage. When the manipulator moves nearby the dynamic singular configuration in each regulation stage, a new suitable active joint will be used to regulate the fault joint.

In summary, to ensure that tasks can be completed after a free-swinging joint failure occurs, a multi-stage regulation strategy for space manipulators is proposed in this paper.First, according to the inertia matrix, Coriolis and centrifugal terms of the dynamics model, an EMRA of active joints over the fault joint is established based on a fuzzy entropy.Second,a multi-stage regulation strategy based on the EMRA is proposed. The multi-stage regulation strategy divides the regulation process into several stages. At every regulation moment,we judge whether the manipulator is located nearby a dynamic singular configuration. If the manipulator tends to move to a dynamic singular configuration in the current stage, the regulation process will be switched into the next stage, and a certain active joint is selected as the regulative joint based on the EMRA to regulate the fault joint.In this way,the the fault joint can be successfully regulated to the desired angle.

Therearethreeadvantagesofthemulti-stageregulationstrategy for space manipulators with a free-swinging joint failure:

1) In selecting the regulative joint, Coriolis and centrifugal terms of the dynamics model for the space manipulator are considered for the first time, making the selection result more in line with the actual regulation process.

2) During the establishment of the EMRA, the fuzzy entropy can eliminate the influence of the manipulator model uncertainty on the EMRA, making the evaluation of regulative ability more precise.

3) A multi-stage regulation strategy based on the EMRA is proposed, successfully regulating the fault joint to the desired angle without huge torque on regulative joints.

In this paper,the following statements are made first:Only one joint fails at a time;Only one active joint is selected as the regulative joint at a time.

The rest of the paper is organized as follows: In Section 2,the EMRA is established by introducing the fuzzy entropy theory, and an active joint with the best regulation ability is selected as the regulative joint. In Section 3, the multi-stage regulation strategy is designed to regulate the fault joint to the desired angle. The numerical simulation results are given in Section 4, and the conclusion is summarized in Section 5.

2. Establishment of EMRA based on fuzzy entropy

To improve the efficiency of the motion transmission during the regulation process, an active joint with the best regulation ability needs selecting as the regulative joint.The local and global coupling indexes can be used to evaluate the regulation ability of active joints. But when the space manipulator is in motion, Coriolis and centrifugal terms should be considered.Therefore, an EMRA will be established to evaluate the regulation ability of active joints.

In this section,through establishing the dynamics model for space manipulators with a free-swinging joint failure,coupling indexes between the fault and active joints are constructed.And then taking into account Coriolis and centrifugal terms of the dynamics model, the EMRA is established based on the fuzzy entropy.

2.1. Dynamics model for space manipulators with a freeswinging joint failure

DCRFAJ is the basis of the establishment of the EMRA. To obtain the DCRFAJ,the dynamics model of the space manipulator with free-swinging joint failure is established firstly. An n-DOF space manipulator attached on the space station is taken as the research object, whose base can be considered as fixed (because the mass and inertia of the space station are much larger than that of the space manipulator23). The simplified model of the space manipulator is shown in Fig. 1.Starting from the base, we number the joints as 1-n successively and denote them as Ji(i=1， 2，...， n). ∑i denotes the coordinate system of Ji, and ∑I denotes the inertial coordinate system.

The dynamics equation of the n-DOF space manipulator is:

where q，˙q，¨q ∈Rn×1denote the joint angle, velocity and acceleration, respectively; M(q)∈Rn×ndenotes the inertia matrix,which is a symmetric positive definite matrix; C(˙q，q)∈Rn×1denotes Coriolis and centrifugal terms; τ ∈Rn×1denotes the joint torque.

When a free-swinging joint failure occurs, all the joints are divided into two parts: fault joints and active joints, and Eq.(1) can be rewritten as:

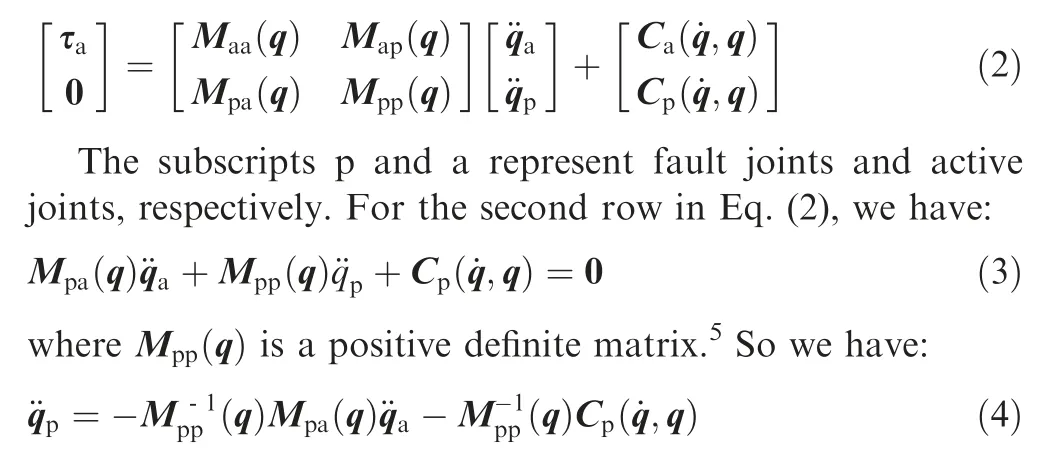
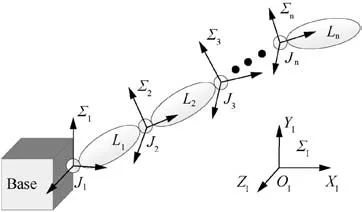
Fig. 1 Simplified model of space manipulator.

The relationship in Eq.(4)is the DCRFAJ.We can see that once the control law¨qaof active joints are given,the acceleration¨qpof fault joints can be calculated.And through integrating¨qp,the corresponding velocity and angle of the fault joints are obtained.

2.2. Establishment of EMRA

To maximize the efficiency of the motion transmission for active joints to fault joints, it is necessary to establish an evaluation model to select an active joint with the best regulation ability as the regulative joint. Taking into account inertia matrix, Coriolis and centrifugal terms of the dynamics model,the EMRA is established based on the fuzzy entropy to select the regulative joint.

where σris the singular value of the matrix Ms.λsis also called as the local coupling index. It describes the coupling degree between fault and active joints under a certain manipulator configuration, and quantitatively reflects the acceleration of fault joints obtained from the active joint.

In this paper, only one joint fails at a time, i.e., m=1.Assume that the fault joint is Jk(k=1，2，...，n), and Eq. (5)can be rewritten as:

The larger λs，iis, the greater the regulation ability of the active joint over the fault joint is.

From Eqs. (5)-(8), the local coupling index changes with the manipulator configuration, and we cannot decide which local coupling index is the largest at all manipulator configurations.Therefore,we should pay more attention to the coupling index in a global sense, to measure the dynamic coupling within the workspace of the manipulator.In this case,a global coupling index is more useful. The global coupling index can be defined as follows:9,10

where the above integral is taken over the entire joint space Θ ∈Rnof manipulators.24

The global coupling index is constructed on the basis of the local coupling index,and it reflects the coupling relationship at all configurations. In this way, the global coupling index can evaluate the regulation ability of each active joint over the fault joint in the whole workspace.

The local and global coupling index can provide a basis for selecting the regulative joint. Both of them are constructed with the inertia matrix of the dynamics model. However,according to Eq.(4),when the space manipulator is in motion during the regulation process, the motion of the fault joint is influenced by not only the inertia matrix, but also Coriolis and centrifugal terms. With the increase of motion velocity,the proportion of Coriolis and centrifugal terms increase,and the influence is more obvious. If the regulative joint is selected by coupling indexes constructed only with the inertia matrix, the selection result would be unreliable.

2.2.2. EMRA

In this section,a new evaluation model of each active joint will be constructed with the inertia matrix,Coriolis and centrifugal terms. Through varying the space manipulator configuration,sets of evaluation information will be generated based on the inertia matrix, Coriolis and centrifugal terms. These sets of evaluation information reflect the regulation ability of active joints from different manipulator configurations. Due to measurement error and unmodeled dynamics of the manipulator, the dynamics model contains some uncertainties16,adding fuzziness to these set of evaluation information. Considering that the fuzzy entropy can eliminate the fuzziness to make a stability evaluation,17it will be adopted to deal with these sets of evaluation information in establishing the EMRA.

Separate the nonlinear term in Eq. (4) to obtain Coriolis term and centrifugal term as follows:

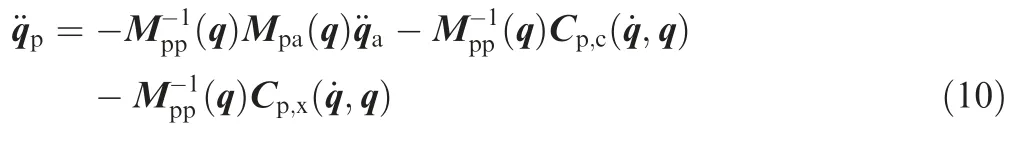
where Cp，c(˙q，q) and Cp，x(˙q，q) denote Coriolis term and centrifugal term, respectively.

Similar to the local coupling index λs，iconstructed with Eqs.(5)-(8), the other two indexes λc，iand λx，iare constructed by Coriolis and centrifugal terms, respectively. Let:

where Mc∈R1×(n-1)， Mx∈R1×(n-1). c¯¨qpand x¯¨qpdenote the acceleration of fault joints from Coriolis term and centrifugal term, respectively.

Make Mc，i，Mx，ibe the i-th element of Mc，Mx,respectively,and then λc，iand λx，ican be written as follows:

Considering the uncertainty of the dynamics model,λs，i， λc，iand λx，iare deviated from the actual value.In another word, λs，i， λc，iand λx，ihave fuzziness. To deal with the fuzziness to establish the EMRA, the fuzzy entropy theory is adopted in this section.

The fuzzy entropy theory is a kind of entropy method,which can determine the weight of every index according to the information provided by the observed values of various indexes.15When applying the fuzzy entropy theory, the first step is to obtain the evaluation of the index by the expert.Although there is fuzziness caused by subjectivity of the expert,a fuzzy entropy theory can be used to eliminate them to obtain a stable evaluation weight. The expert evaluation of the index includes the most conservative evaluation, the most possible evaluation and the most optimistic evaluation.They can affect the regulation ability of active joints.

Therefore, take active joints as expert evaluation indexes.With λs，i， λc，iand λx，iselected as the most conservative evaluation,the most possible evaluation and the most optimistic evaluation, respectively, the EMRA based on the fuzzy entropy is established. The establishment steps of the EMRA are as follows.

(1). Triangular fuzzy weight.

(A) Establish the triangular fuzzy matrix.Assume that there are l experts evaluating η (η=n-1)active joints.For l,we have:

Taking aij，bijand cijevaluated by the j-th expert to the i-th active joint as the most conservative evaluation,the most possible evaluation and the most optimistic evaluation, respectively. Namely, aij，bijand cijdenote λs，i， λc，iand λx，i,respectively.To evaluate the regulative ability of the i-th active joint, the corresponding expert evaluation is calculated on the premise of locking other active joints.Based on Eq.(8)and Eq.(12),λs，i， λc，iand λx，iare influenced by the angle/velocity of the i-th active joint and the fault joint.In this section,with the i-th active joint and the fault joint moving at a certain velocity,we calculate l expert evaluations of the i-th active joint by traversing the relative angle between the i-th active joint and fault joint.Namely,if the active joint number is in front of the fault joint, the fault joint angle is traversed to calculate expert evaluations, otherwise the active joint angle is traversed.

Therefore, by traversing joint angle within the joint limit range,aij，bijand cijare obtained,forming an initial evaluation matrix (triangular fuzzy matrix) as follows:

(B) Determine the expert evaluation weight set.Taking ωjas the proportion of the evaluation weight of the j-th expert over active joints in the comprehensive evaluation, we obtain the expert evaluation weight set:

In this paper, the fault and active joint can exist at any mutual position, so we can define that the evaluation weight of each active joint is equal in the comprehensive evaluation,i.e., ωj=1/l.

(C) Form the fuzzy synthesis matrix. Taking ω ⊙X as the fuzzy synthesis result of evaluation value and evaluation weight, the fuzzy synthesis matrix is formed as follows:

(D) Determine the triangular fuzzy weight.According to the characteristics of triangular fuzzy number,25the initial fuzzy weight of the i-th active joint is determined by the elements of the fuzzy synthesis matrix T, that is:

Normalizing di, we have:

(2). Entropy weight.

(A) Determine the total entropy of the index. Based on the initial evaluation matrix X,its elements are standardized as follows:

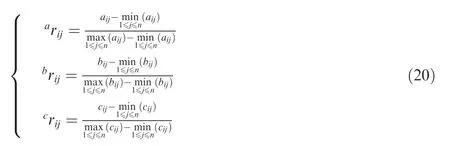
Then the entropy value of the i-th active joint is determined as follows:

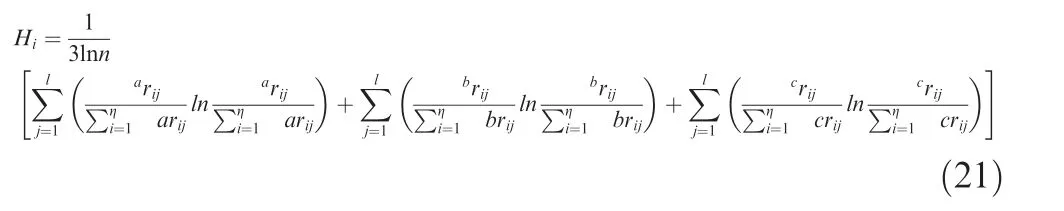
(B) Determine the entropy weight of the index (normalization).The entropy weight of the i-th active joint is determined as follows:

(3). Combined weight. By combining the above triangular fuzzy weight ξiand entropy weight hi, the combined weight of the i-th active joint is determined as follows:

During the establishment of the EMRA, the fuzzy evaluation information, caused by the model uncertainty, is processed quantitatively. And with the fuzzy entropy, the influence of the manipulator model uncertainty on the EMRA is eliminated,making the evaluation of the regulative ability of active joints more precise.

2.3. Selection and analysis of the regulative joint

To improve the regulation efficiency, an active joint with the best regulation ability can be selected as the regulative joint based on the EMRA.

wmaxmeans that the corresponding active joint has the best regulation ability,and it is considered to be selected as the regulative joint. The efficiency in regulating the fault joint to the desired angle is maximized,and as long as a small acceleration is given to this active joint, the fault joint can obtain a large acceleration.

To verify that the selection of the regulative joint based on the EMRA is more precise than that based on the global coupling index, the following measures are carried out. An acceleration at the i-th active joint will be generated to provide an acceleration ¨q′pfor the fault joint. Through traversing the relative angle between the fault and active joint, the acceleration sequence ¨q′a，iof each active joint is obtained, and then the average value of ¨q′a，iis calculated. The larger the final evaluation weight or global coupling index of each active joint is,the smaller the corresponding average acceleration is. If the order of the average acceleration is consistent with that of the final evaluation weight for active joints, the effectiveness of the EMRA is verified.

It is worth noting that when the manipulator is near a singular configuration,if a certain acceleration is required to generate at the fault joint, the acceleration of the active joint calculated by the dynamics model is much larger than that calculated not near the singular configuration.During the regulation process of the fault joint, we generally avoid the singular configuration of the manipulator. So it is necessary to deal with the active joint acceleration calculated in the vicinity of the singular configuration, which is also called as singular acceleration. In this paper, quartileyy26is used to deal with the singular acceleration. The specific steps are as follows:

Step 4. Traverse all accelerations of active joints, and deal with the singular accelerations according to step 1-3.And then calculate the corresponding average acceleration,obtaining the average acceleration ¯¨q′a，iof each active joint.

From the above steps, the singular acceleration is dealt with,and the order of the average acceleration for active joints is obtained.

3. Multi-stage regulation strategy for space manipulators

With selecting the regulative joint based on the EMRA, the fault joint will be regulated to the desired angle by planning the motion of the regulative joint. In this section, we first designed a two-phase control method for the underactuated manipulator, to stabilize the regulative joint and fault joint simultaneously when the fault joint reaches at the desired angle. For the case that the manipulator tends to move to a dynamic singular configuration during the regulation process,a multi-stage regulation strategy is proposed. The multi-stage regulation strategy divides the regulation process into several stages, and during each regulation stage, a certain active joint is selected as the regulative joint based on the EMRA. In this way, the fault joint is regulated to the desired angle without huge torque on regulative joints.

3.1. Control method of the space manipulator

Without the gravity for space manipulators, the free-swinging joint and regulative joint cannot be simultaneously stabilized at a certain angle via a smooth control law on the regulative joint. In this section, we divide the control process into reaching phase and stabilizing phase.In the reaching phase,the fault joint will be controlled to quickly reach nearby the desired angle through a smooth control law on the regulative joint.In the stabilizing phase, an iterative steering control law is designed for the regulative joint,to stabilize the regulative joint and fault joint simultaneously when the fault joint reaches at the desired angle.

In the reaching phase, an auxiliary input vector is introduced according to the trajectory error of the fault joint, to construct the control law of the regulative joint. Assume that only one active joint is used to regulate the fault joint at a time,while keeping other active joints still. Based on Eq. (2), we have:

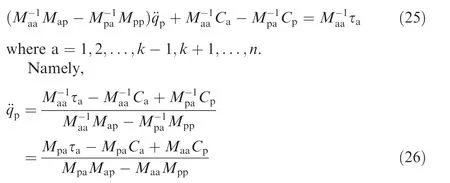
Let e represents the error feedback of the fault joint angle:

Combining Eq.(4)and Eq.(28),the acceleration of the regulative joint torque is obtained, as expressed as follows:

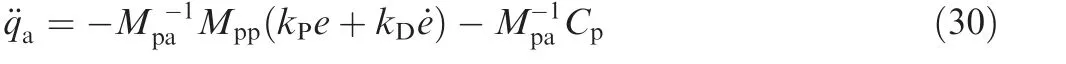
By integrating Eq. (26) and Eq. (30) with the numerical method,the velocity and angle of the fault joint and regulative joint are obtained, respectively.

where t represents the running moment,ω represents the angular frequency,Arepresents the amplitude of the periodical input, and qa0represents the regulative joint angle at the end of the reaching phase.

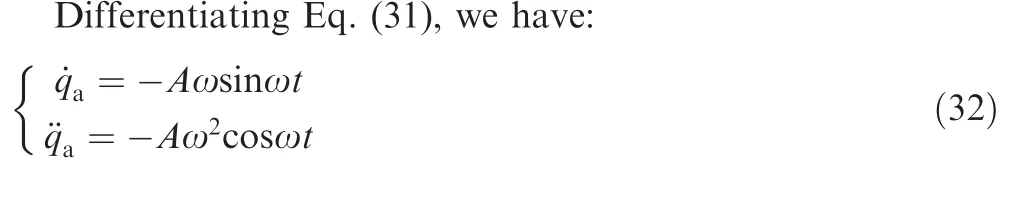
According to Refs. [27-28], when the actuated joint move as Eqs.(31)and(32),the free-swinging joint shows a character of spiral motion,and its final position will shift from the initial position. Based on this characteristic, the free-swinging joint can reach a certain position by the harmonic motion of the actuated joint.

Substitute Eq. (28) and Eq. (32) into Eq. (4), and we have:

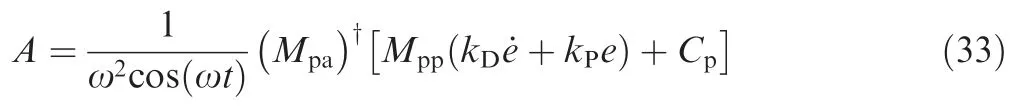
As it can be seen in Eq. (33), the amplitudeAchanges at every moment based on the feedback of the free-swinging joint. Combining Eq. (4), Eq. (32) and Eq. (33), the motion of the manipulator is obtained as follows:

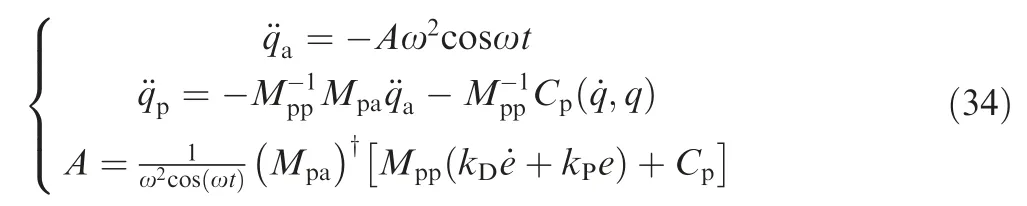
where the velocity of the free-swinging joint at the desired angle is equal to zero, i.e.,=0.

Based on the two-phase control method,the fault joint will be regulated to the desired angle, and the regulative joint and fault joint are stabilized simultaneously.

3.2. Multi-stage regulation strategy based on the EMRA

The multi-stage regulation strategy divides the regulation process into several stages, and during each regulation stage,a certain active joint is selected as the regulative joint based on the EMRA.At every regulation moment,we judge whether the manipulator is located nearby a dynamic singular configuration.If the manipulator tends to move to a dynamic singular configuration in the current stage, it means that the current regulative joint is not enough to regulate the fault joint. Then the regulation process will be switched into the next stage,and another active joint is selected as the new regulative joint to regulate the fault joint. Repeat these steps until the fault joint is regulated to the desired angle.

In every current regulative stage, based on the EMRA established in Section 2.3,we select an active joint with the best regulation ability as the current regulative joint.With the twophase control method designed in Section 3.1, the regulative joint and fault joint will move with the feedback of their trajectories.Here,we use the regulative joint torque τaas an index to reflect its regulation ability. When τaexceeds its initial torque τ0,the current regulative joint is hard to regulate the fault joint at this moment.In this case,the regulation process is switched into the next stage, and another active joint is selected as the new regulative joint based on the EMRA. Similarly, the fault joint will be regulated to its desired angle with the two-phase control method.

It is noted that at the beginning of a new stage,the last regulative joint is in motion,and it should be stopped slowly.Plan the acceleration of the regulative joint in the new stage as follows:

where subscript L denotes the last regulative joint.

By integrating Eq. (35) with the numerical method, the velocity and angle of the last regulative joint are obtained.And then Eq. (2) can be rewritten as follows:

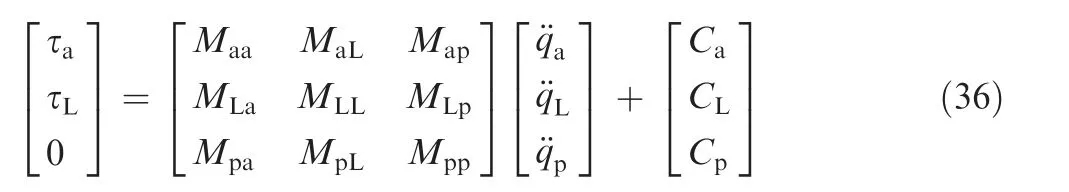
In this way,during the new stage,the motion of the manipulator in Eq.(28),Eq.(30),and Eq.(34)is changed as follows:

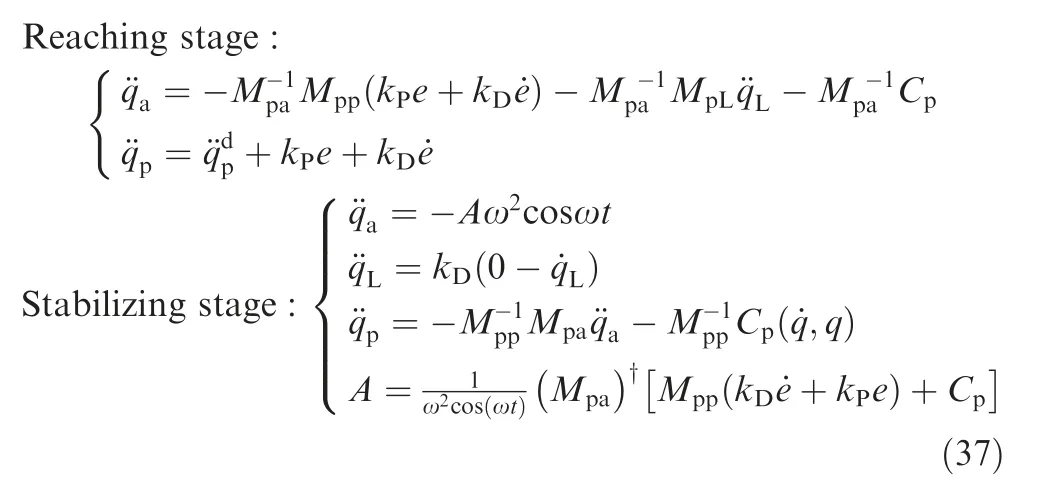
In summary, the multi-stage regulation strategy for space manipulators with a free-swinging joint failure is shown as follows.

Step 1.Based on the ERMA,select an active joint with the best regulation ability as the regulative joint.

Step 2.With the two-phase control method designed in section 3.1,the regulative joint and fault joint are moved with the feedback of their trajectories.

Step 3.Compared the torque of the regulative joint τawith its initial torque τ0.If |τa|＞τ0,go to step 4,otherwise go to step 5.

Step 4. Switch the regulation process into the next stage,select a new regulative joint based on the EMRA,and go back to step 2.

Step 5.The fault joint is regulated to the desired angle,and the regulative joint and fault joint are stabilized simultaneously at the same time, completing the regulation of the underactuated manipulator.

4. Simulations

Aiming at the multi-stage regulation strategy of space manipulators with a free-swinging joint failure, simulation experiments are carried out with a 7-DOF space manipulator, as shown in Fig. 2. Its DH parameters and dynamic parameters are shown in Table 1 and Table 2, respectively.

Set the physical limit of each joint as [-180°， 180°].Assume that the fourth joint J4fails, and the configuration of the space manipulator at the failure moment is[40°，150°，60°，-60°，15°，-85°，40°].

4.1. Establishment of the EMRA

4.1.1. Analyzing coupling indexes between the joints

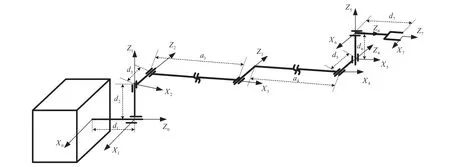
Fig. 2 Structure of 7-DOF space manipulator.

Table 1 DH parameters of 7-DOF space manipulator.

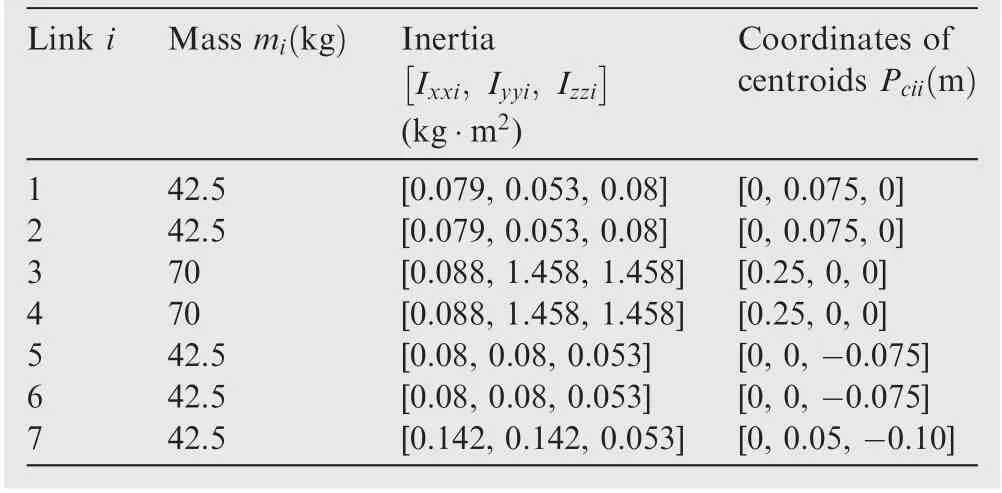
Table 2 Dynamics parameters of 7-DOF space manipulator.

For each active joint, by traversing the relative angle between the fault joint and active joint with a step length of 1°within the joint limit range,the local coupling index is calculated according to Eq. (8). Fig. 3 shows the curves of the local coupling index changing with the joint angle.We can see that the order of the local coupling index value is inconsistent at different angle. For example, when the joint angle is 10°, the order of the local coupling index value is λg，3＞λg，2＞λg，1＞λg，5＞λg，6＞λg，7. But when the joint angle is 150°, the order of the local coupling index value is λg，1＞λg，2＞λg，3＞λg，5＞λg，7＞λg，6. In another word, no local coupling index is always larger than else at any joint angle.Now we calculate the global index according to Eq.(9),and the results are shown in Table 3. From Table 3, the order of the global index is obtained as follows:

The local index and global index reflect the coupling degree between the fault and active joint when the manipulator is in a static state. However, the space manipulator is in motion during the regulation process, and the motion of the fault joint is also influenced by nonlinear terms in the dynamics equation.Set the velocity of the fault and active joint as 0.2°/s, the changes of the nonlinear terms produced by different active joints while regulating the fault joint are obtained, as shown in Fig.4.Combining Fig.3 and Fig.4,the motion of the fault joint is affect by the nonlinear term based on Eq. (4). Therefore, Coriolis and centrifugal terms should be taken into account to select the regulative joint.

4.1.2. Selecting the regulative joint based on the EMRA

Through traversing the relative angle between the fault joint and active joint, the number of the expert is obtained as follows:

Fig. 4 Changes of nonlinear terms.

Set the velocity of the fault joint and active joint as 0.2°/s,based on Eq. (8) and Eq. (10), λs，i， λc，iand λx，iare calculated,forming the initial evaluation matrix afterwards. The evaluation weight given by each expert to the active joint is equally important in the comprehensive evaluation, so we have:

According to the establishment steps of the EMRA in Section 2.2, the final evaluation weight set of active joints is shown in Table 4. According to Table 4, the order of the final evaluation weight of active joints is:

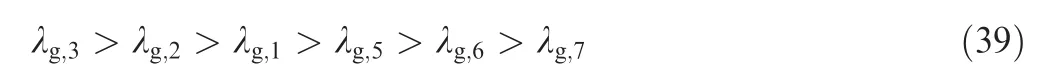
To verify that selection of the regulative joint based on the EMRA is more reliable than that based on the global coupling index,the following experiment is carried out.Assume that the acceleration of the fault joint obtained from the active joint is=0.15°/s. The acceleration sequence ¨q′a，iof each active joint is obtained, as shown in Fig. 5. There are some accelerations much larger than the others, which means that these accelerations are the singular accelerations. Quartile is used to deal with the singular acceleration. According to Fig. 5,set k=[k1，k2，...，k6]T=[3， 2.5， 3， 2， 1.5， 2.5]T, and the results are shown in Fig. 6.

Calculate the average acceleration of each active joint, as shown in Table 5. From Table 5, the order of the average acceleration of active joints is obtained as follows:

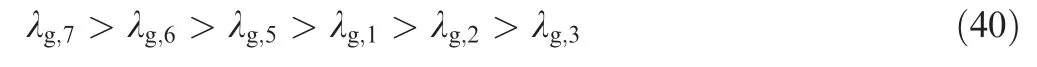
Eq. (40) is consistent with the order of the final evaluation weight of active joints in Eq. (39). The results verify the effectiveness of the EMRA established in this paper.

Fig. 5 Acceleration of each active joint.

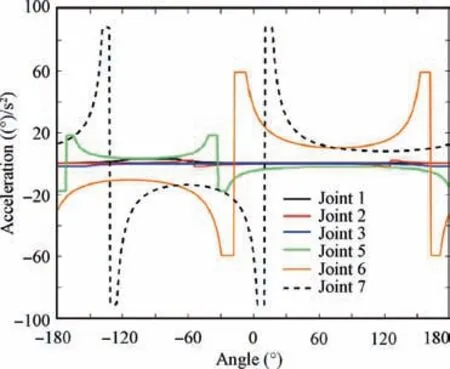
Fig. 6 Acceleration of each active joint after dealing with singular acceleration.

4.2. Multi-stage regulation of the underactuated manipulator

Assume the desired angle of the fault joint is qdp=30°. From Table 4, the final evaluation weight of J3is the largest, i.e.,J3owns the best regulation ability to the fault joint.Therefore,J3is selected as the regulative joint to regulate the fault joint.Set the boundary between the reaching phase and stabilizing phase as eth=2°, the angular frequency as ω=2π, and the proportionality coefficients of PD controller as kP=1， kD=1.8. Through the two-phase control method designed in Section 3.1, the trajectories of the fault joint and regulative joint are shown in Fig. 7.

In Fig. 7, when 0 ≤t ≤4.55 s, the underactuated manipulator moves in the reaching phase, and the fault joint quickly reaches nearby the desired angle. When t ＞4.55 s, the underactuated manipulator switches into the stabilizing phase. The regulative joint makes an iterative steering motion to regulate the fault joint to the desired angle,and at last two of them are stabilized simultaneously.

Table 4 Final evaluation weight set of active joints.

Table 5 The average acceleration of active joints.

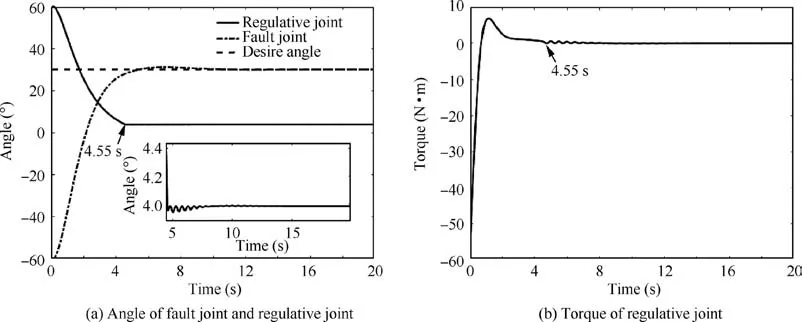
Fig. 7 Trajectories of fault joint and regulative joint when qdp =30°.

Fig.8 Change of regulative joint torque with just one regulative joint when qdp =155°.

The regulation process in Fig. 7 shows that the fault joint can be regulated to the desired angle through just one stage with one active joint. We can see that the dynamic singular configuration did not occur during the regulation process.Now we assume that the desired angle of the fault joint is=155°. We first use J3to regulate the fault joint. The simulation result is shown in Fig. 8. Starting at about 3.5 s, the torque of J3increases quickly, and τa=92390 N·m at 3.9 s.It means that the manipulator tends to move to a dynamic singular configuration in the current stage, and J3does not have enough regulative ability to regulate the fault joint any more.Therefore,it is necessary to select another active joint to regulate the fault joint.

Using the multi-stage regulation strategy proposed in this paper, the simulation results are shown in Fig. 9. When 0 ≤t ≤3.5 s, J3is selected as the regulative joint to regulate the fault joint. When t ＞3.5 s, the regulation process is switched into the next stage and J2is selected as the new regulative joint with Table 4.At last,the fault joint is regulated to the desired angle, and the fault joint and regulative joint are also stabilized simultaneously.

Fig. 9 Trajectories of fault joint and regulative joint with multi-stage regulation strategy.

Table 6 Final evaluation weight set of active joints.

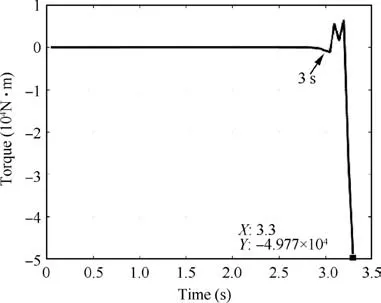
Fig. 10 Change of fourth joint torque with just one regulative joint when the third joint fails.

To verify the generality of the multi-stage regulation strategy, we assume that the third joint J3fails.

Similar to establishing the EMRA in section 4.1.2, we obtain the final evaluation weight set of active joints as shown in Table 6.

Assume the desired angle of the third joint is qdp=105°.According to Table 6,We first use J4to regulate the fault joint.The simulation result is shown in Fig.10.Starting at about 3 s,the torque of J4increases quickly, and |τ4|=49770 N·m at 3.3 s. It means that J4does not have enough regulative ability to regulate the fault joint any more. Now we use the multistage regulation strategy to regulate the fault joint, and the simulation result is shown in Fig. 11.

In Fig. 11, when 0 ≤t ≤2.7 s, J4is selected as the regulative joint to regulate the fault joint. When t ＞2.7 s, the regulation process is switched into the next stage and J1is selected as the new regulative joint. At last, the fault joint is regulated to the desired angle. The above results verify the effectiveness of the multi-stage regulation strategy proposed in this paper.

5. Conclusions

For space manipulators with a free-swinging joint failure, a multi-stage regulation strategy is proposed to regulate the fault joint to the desired angle.First,taking into account the inertia matrix, Coriolis and centrifugal terms of the dynamics model,an EMRA of active joints over the fault joint is established based on a fuzzy entropy. Second, a multi-stage regulation strategy based on the EMRA is proposed,which divides the regulation process into several stages. At every regulation moment, we judge whether the manipulator is located nearby a dynamic singular configuration. If the manipulator tends to move to a dynamic singular configuration in the current stage,the regulation process will be switched into the next stage, and another active joint with suitable regulative ability is selected as the regulative joint.In this way,the fault joint is successfully regulated to the desired angle without huge torque on regulative joints.

The multi-stage regulation strategy possesses three advantages as follows.

(1) In selecting the regulative joint, Coriolis and centrifugal terms of the dynamics model for the space manipulator are considered for the first time, making the selection result more in line with the actual regulation process.

(2) During the establishment of the EMRA, the fuzzy entropy can eliminate the influence of the manipulator model uncertainty on the EMRA, making the evaluation of regulative ability more precise.

(3) A multi-stage regulation strategy based on the EMRA is proposed, successfully regulating the fault joint to the desired angle without huge torque on regulative joints.

Fig. 11 Trajectories of fault joint and regulative joint with multi-stage regulation strategy when third joint fails.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the Fundamental Research Funds for the Central Universities of China (No. 2019PTB-012), the Science and Technology Foundation of State Key Laboratory of China (No. 6142210180302), and the National Natural Science Foundation of China (No. 51975059).