Scaling of interaction lengths for hypersonic shock wave/turbulent boundary layer interactions
Yuting HONG, Zhufei LI, Jiming YANG
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
KeywordsHypersonic flow;Interaction length;Scaling laws;Separation criterion;Shock wave/turbulent boundary layer interactions
Abstract The interaction length induced by Shock Wave/Turbulent Boundary-Layer Interactions(SWTBLIs)in the hypersonic flow was investigated using a scaling analysis,in which the interaction length normalized by the displacement thickness of boundary layer was correlated with a corrected non-dimensional separation criterion across the interaction after accounting for the wall temperature effects.A large number of hypersonic SWTBLIs were compiled to examine the scaling analysis over a wide range of Mach numbers,Reynolds numbers,and wall temperatures.The results indicate that the hypersonic SWTBLIs with low Reynolds numbers collapse on the supersonic SWTBLIs,while the hypersonic cases with high Reynolds numbers show a more rapid growth of the interaction length than that with low Reynolds numbers. Thus, two scaling relationships are identified according to different Reynolds numbers for the hypersonic SWTBLIs. The scaling analysis provides valuable guidelines for engineering prediction of the interaction length, and thus, enriches the knowledge of hypersonic SWTBLIs.
1. Introduction
Shock Wave/Turbulent Boundary-Layer Interactions(SWTBLIs) have been extensively investigated in the past several decades,1and progress in both mean and unsteady flows are reviewed by Dolling and Brusniak,2,3Clemens and Narayanaswamy,4and Gaitonde.5SWTBLI-induced separation is an undesirable phenomenon that causes severe pressure/heating loads6and flow unsteadiness across an interaction.4The interaction length is generally used as an important characteristic length to normalize the unsteadiness of the separation for different configurations,4including compression corners and shock reflections. Moreover, the oscillation extent of the separation shock has been reported to depend on the interaction length.7Thus, knowledge of the interaction length is of great significance in SWTBLIs.
To assess interaction lengths induced by various configurations, a scaling method was proposed by Souverein et al.,8which correlates the interaction length with the pressure jump across the SWTBLIs.It has been demonstrated that the majority of documented interaction lengths on adiabatic walls collapse well when using this scaling. Subsequently, a correction for nonadiabatic walls was made by Jaunet et al.9because the wall temperature affects the onset of flow separation and the interaction length. However, both Souverein’s scaling and Jaunet’s correction were mainly examined in supersonic SWTBLIs, which creates an obvious motivation to know whether these scaling methods can be used for hypersonic SWTBLIs.
The amount of data in hypersonic SWTBLIs is much less than that in supersonic flows. Holden et al.10,11conducted a series of experiments using compression corners and shock reflections, which duplicated hypersonic flight conditions with high Reynolds numbers. Elfstrom,12Coleman and Stollery,13Schu¨lein,14Lee and Wang15observed separated flows caused by different compression corners and shock reflections,respectively.Recently,Schreyer et al.16measured a separated flow on a compression corner using Particle Image Velocimetry (PIV).Although numerical simulations can enrich the understanding of hypersonic SWTBLIs, accurately predicting hypersonic SWTBLIs remains a challenge.1Simulations using Reynolds-Averaged Navier-Stokes (RANS) equations have shown some limitations in turbulence modeling as reported by Roy and Blottner,17although a recent work by Roy,18Tu,19and Pasha20et al. made progress. Thus, high-fidelity simulations are preferred when assessing hypersonic SWTBLIs, although the majority of works remain limited by low Reynolds numbers. The Direct Numerical Simulation (DNS) performed by Tong et al.21and Large Eddy Simulations (LES) performed by Bhagwandin et al.22were focused on compression corner induced separations with large flow Mach numbers. Recently,Volpiani et al.23performed a DNS of shock reflections, in which the Schu¨lein experiments14were replicated and the wall temperature effects on flow separation were examined. Interestingly, Bhagwandin et al.22and Volpiani et al.23compared their separation lengths with Souverein’s scaling and confirmed that the wall temperature effects must be considered for hypersonic SWTBLIs.
It is clear that comprehensive data of hypersonic SWTBLIs should be employed to examine the potential of Souverein’s scaling method. In this paper, a number of hypersonic SWTBLIs from low to high Reynolds numbers are compiled and discussed in an effort to ultimately devise new features for scaling the interaction length.
2. Methods
The scaling method of the interaction length in SWTBLIs proposed by Souverein et al.8is employed here, which provides a context for further analysis.For a separated flow induced by a compression corner or a shock reflection on a flat plate, the interaction length L is commonly defined as the distance from the mean position of the separation shock foot to the corner or to the extrapolated wall impinge point of the incident shock.7,8Following the scaling procedures reported by Souverein et al.,L is initially normalized by the displacement thickness of the upstream turbulent boundary layer δ*, which takes the form of Eq. (1).
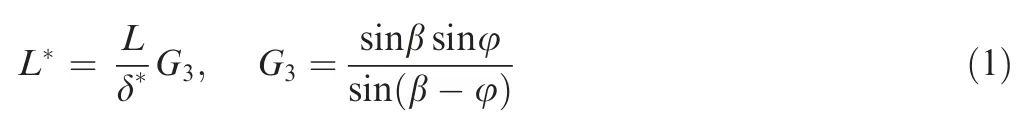
where L* is the nondimensional interaction length, β is the shock angle,and φ is the flow deflection angle.Next, a nondimensional separation criterion Seis introduced to correlate with the pressure jump ΔP across the interaction, which takes the form of Eq. (2).

where k is an empirical constant related to the Reynolds number based on momentum thickness Reθand qeis the freestream dynamic pressure. As suggested by Souverein et al., k=2.5 and 3.0 for Reθ>104and Reθ≤104, respectively. The values of k were obtained based on a number of supersonic SWTBLIs with determined onset of flow separation. After implementing these scaling procedures, Souverein et al. found that various interaction lengths in supersonic SWTBLIs collapse well into Eq. (3).

Note that the value of k in Souverein’s scaling method is validated for adiabatic walls. In reality, the wall temperature significantly influences the separation and the interaction length,9,23especially for an isothermal wall.However,few data have been reported with determined onset of flow separation for nonadiabatic walls in supersonic and hypersonic SWTBLIs. It is inadvisable to statistically obtain the values of k following the procedures reported by Souverein et al.8Jaunet et al.9introduced nonadiabatic wall effects into Souverein’s scaling method by correcting k,in which the wall friction coefficient in the upstream boundary layer was correlated with k. The corrected constant kcis given in Eq. (4), which is derived from the free interaction theory;24for more details,one can refer to Ref.9.

where Twis the wall temperature, Teis the static temperature,and Rexis the local Reynolds number.Once kcis obtained and substituted in Eq.(2),the separation criterion Seis corrected toFor a better description, a general parameter k* is used to unify k and kc. Similarly, another general parameter S*eis employed to represent Sefor adiabatic walls and Scefor nonadiabatic walls. It should be emphasized that neitherSouverein’s scaling nor Jaunet’s correction has been widely applied in hypersonic SWTBLIs, especially for high Reynolds numbers (Reθ>104). Therefore, the major goal in this paper is to examine these scaling methods in the hypersonic regime,which is subsequently discussed.
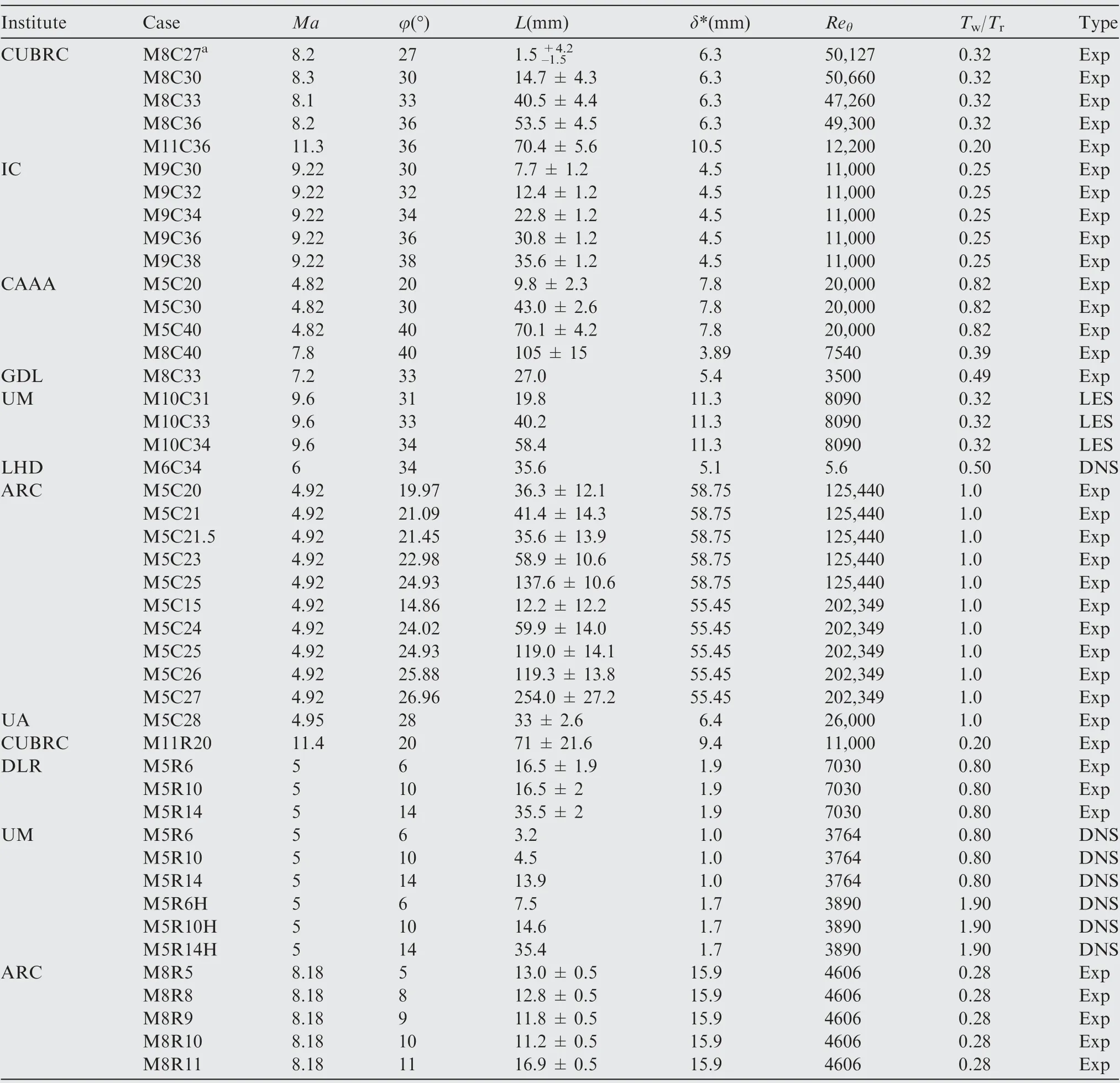
Table 1 Data sets of hypersonic SWTBLIs.
3. Data sets
The collected hypersonic SWTBLIs are listed in Table 1,including the experiments (Exp) conducted at the Calspan-University of Buffalo Research Center (labeled CUBRC),10,11the Imperial College London (labeled IC),12,13the China Academy of Aerospace Aerodynamics (labeled CAAA),15,26the Princeton Gas Dynamics Laboratory (labeled GDL),16the German Aerospace Center (labeled DLR),14the Ames Research Center (labeled ARC) of the National Aeronautics and Space Administration (NASA),27,28and the University of Texas at Austin (labeled UA).29Moreover, the LES and DNS of hypersonic SWTBLIs reported by the University of Maryland (labeled UM)22,23and the State Key Laboratory of High Temperature Gas Dynamics (labeled LHD)21are adopted for comparisons. All cases in Table 1 are named by the nominal Mach number (M), the configuration (C-Compression corner, R-Shock reflection), and the flow deflection angle (φ). Three cases in the UM23study have a heated wall and are named with a suffix H.
The challenge in this study is estimating the interaction length L, as quantitative scales in images of the mean flow(e.g.,schlieren)are lacking in most cases.Instead,the position of wall pressure that first increases above the freestream static pressure is regarded as the mean position of the separation shock foot. Although minor discrepancies are introduced in the origin of the interaction,it has been shown that the impact on the overall interaction length can be ignored.8Specifically,for the experimental case with wall pressure measurements,the middle point between two adjacent pressure transducers that capture the first jump above the freestream static pressure is used as the separation shock foot.Thus,an error bar is defined as the half distance between the two adjacent pressure transducers. The ending point of the interaction is the same as that defined in Section 2. Moreover, the GDL and UM cases merely provided separation lengths,16,22,23which are regarded as the interaction length in this study.
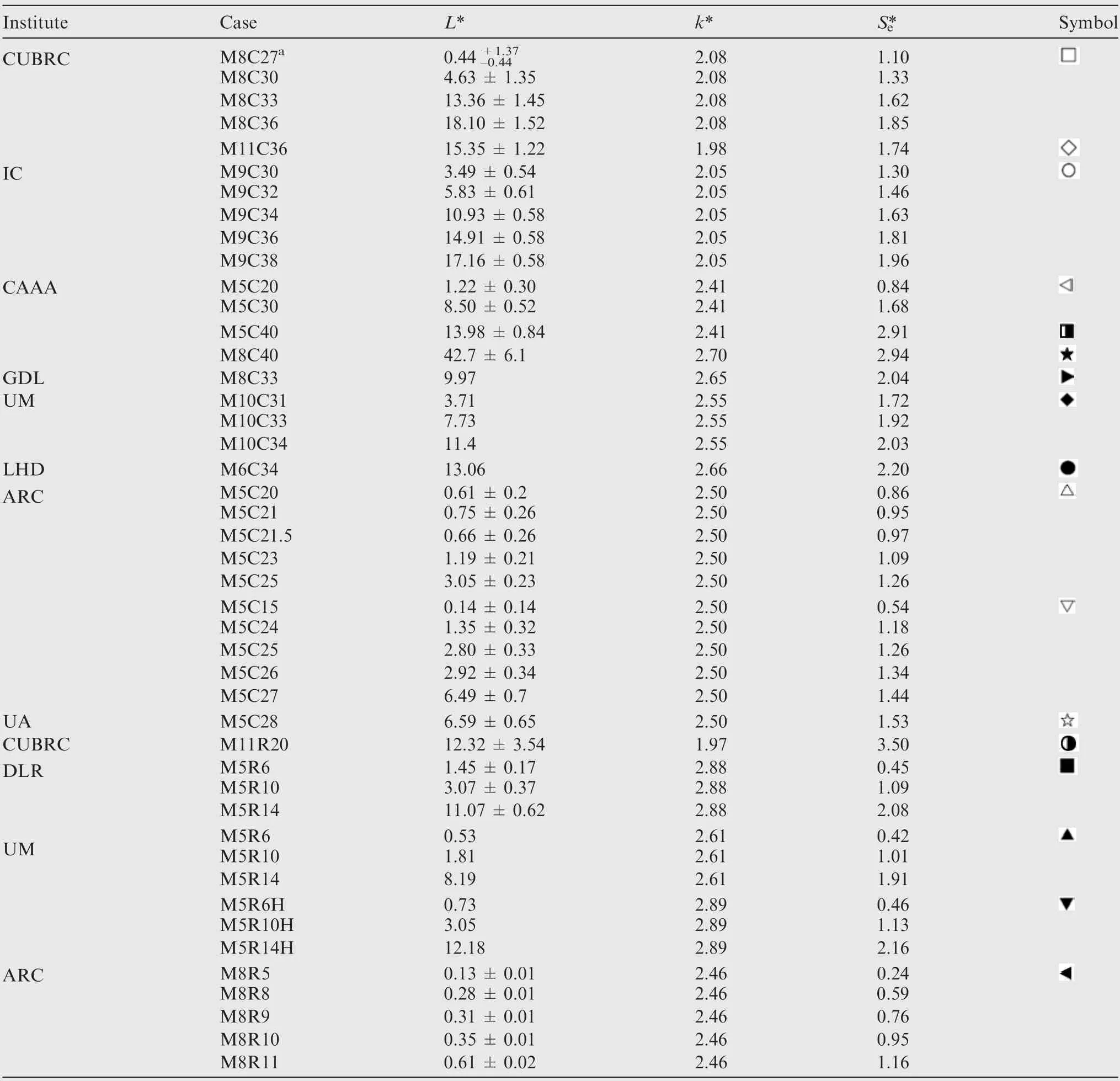
Table 2 Scaled parameters for hypersonic SWTBLIs.
The parameters required to scale the interaction length L,such as δ*, Reθ, and wall-to-recovery-temperature ratio Tw/Tr, are also listed in Table 1. All numerical cases (i.e., UM and LHD) and the experiments in DLR, UA and ARC provided the values of δ* and Reθ, whereas these two parameters were not well documented in the literature for the remaining cases. Thus, the simulations conducted by Brown30are used for the CUBRC cases. Estimations of δ*25and Reθ31based on the reference-temperature method and the power-law velocity profile32are used for the IC,GDL, and CAAA cases.
As shown in Table 1, the data of hypersonic SWTBLIs range from low to high Reθ. All cases are classified into two categories using the criterion of whether Reθ≤104, which is helpful in the selection of k according to Souverein et al.8.The scaling of interaction lengths for hypersonic SWTBLIs is discussed in Section 4.
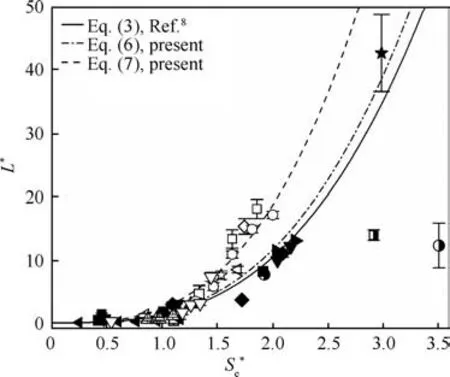
Fig. 1 Scaling of interaction lengths for hypersonic SWTBLIs.
4. Scaling of interaction length
The scaled interaction length L*,the constant k*,and the separation criterion S*efor hypersonic SWTBLIs are calculated(see Section 2) and listed in Table 2, where the solid symbols denote the data with low Reynolds numbers(Reθ≤104),while the hollow and semisolid symbols denote the data with high Reynolds numbers (Reθ>104). All data and corresponding symbols in Table 2 are plotted in Fig.1 to present an overview of the evolution of the scaled interaction lengths,which fundamentally expand the Mach number range investigated by Souverein et al.8. For comparison, Souverein’s fitting line to Eq.(3) is plotted in Fig. 1 using a solid line.
As shown in Fig.1,the hypersonic data with low Reθ(solid symbols)roughly follow the Souverein’s scaling after using the S*e,which indicates that the correction for wall temperatures is neccessry for hypersonic SWTBLIs.Brown33reported that the expansion waves originating from the trailing edge of the incident-shock-generator caused the much smaller L* in the ARC cases(denoted by the left-solid triangles in Fig.1).Thus,a new fitting line to Eq. (6) is proposed to produce a better agreement for the low Reθdata without the ARC cases,which has a determination coefficient (R-squared) of 0.96 and is shown as the dash-dot line in Fig. 1.

Interestingly, the higher Reθcases (hollow symbols) do not collapse on the lower Reθcases(solid symbols)in Fig.1.Moreover,the cases M5C40 and M11R20(semisolid symbols)deviate far away from other cases. The presence of threedimensional effects in the experiment of M5C40 is the most reasonable cause of this deviation, which has been reported by Li.26For the case of M11R20, Marvin et al.34found that the expansion waves originating from the trailing edge of the incident-shock-generator were responsible for the immature interaction-length. Thus, a new fitting line to Eq. (7) is proposed for the high Reθhypersonic data without the cases M5C40 and M11R20, which has a determination coefficient(R-squared) of 0.89 and is shown as the dashed line in Fig. 1. The larger coefficient indicates a more rapid growth of the interaction length than that of low Reθcases.

5. Conclusions
A number of hypersonic SWTBLIs across a large range of Reynolds numbers, Mach numbers, and wall temperatures are compiled for scaling the interaction length. After the correction of the separation criterion for nonadiabatic walls, the scaling by Souverein et al.8was found to work well for the cases with low Reynolds numbers in the hypersonic regime,although the new scaling relationship of Eq.(6)yields a better performance.This finding suggests that the scaling relationship for both adiabatic and nonadiabatic walls can be unified after the correction of the wall temperature. However, the hypersonic SWTBLIs with high Reynolds numbers collapse into a new scaling relationship of Eq. (7). The two scaling relationships indicate that the Reynolds number plays a crucial role in the scaling analysis. This study enriches the knowledge of the interaction length induced by hypersonic SWTBLIs and provides valuable guidelines for engineering applications.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Nos. 11772325 and 11621202).
 CHINESE JOURNAL OF AERONAUTICS2021年5期
CHINESE JOURNAL OF AERONAUTICS2021年5期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Ferrofluid moving thin films for active flow control
- Preliminary study on heat flux measurement data of TT-0 flight test
- An analysis and enhanced proposal of atmospheric boundary layer wind modelling techniques for automation of air traffic management
- Jet sweeping angle control by fluidic oscillators with master-slave designs
- Hot deformation behavior and microstructure evolution of the laser solid formed TC4 titanium alloy
- Electrochemical trepanning with an auxiliary electrode
