Three-dimensional cooperative guidance strategy and guidance law for intercepting highly maneuvering target

Ziyn CHEN, Jinglong YU,*, Xiwng DONG,b, Zhng REN,b

a School of Automation Science and Electrical Engineering, Science and Technology on Aircraft Control Laboratory,Beihang University, Beijing 100191, China

b Beijing Advanced Innovation Center for Big Data and Brain Computing, Beihang University, Beijing 100191, China

KEYWORDS Acceleration constraint;Cooperative interception;Coverage strategy;Guidance law;Highly maneuvering target

Abstract Cooperative interception of the target with strong maneuverability by multiple missiles with weak maneuverability in the three-dimensional nonlinear model is studied. Firstly, the three-dimensional nonlinear model of cooperative guidance is established. The three-dimensional reachable region is represented composed of lateral acceleration and longitudinal acceleration in the two-dimensional coordinate system. Secondly, the problem of the multiple missile’s reachable coverage area is transformed into the problem of cooperative coverage. A cooperative coverage strategy is proposed and an algorithm for quickly calculating the number of required missiles is designed. Then, the guidance law based on the cooperative coverage strategy is proposed, and it is proved that cooperative interception of the target can be achieved under the acceleration limit.Moreover, the relations among the number of missiles, the initial array position of terminal guidance and the coverage area of the target’s large maneuver are analyzed. The dynamic adjustment strategy of guidance parameters is proposed to reduce the guidance error.Finally,simulation results show that multiple missiles with low maneuverability can achieve effective interception of target with strong maneuverability through the proposed cooperative strategy and cooperative guidance method.

1. Introduction

In recent years,as the anti-missile system gradually improving,the single missile interception becomes more and more difficult. Thus, the multiple missile cooperative guidance has become one of the most important research focuses in the guidance field.1The development of multiple missiles cooperative guidance technology has formed two architectures:two-layer cooperative guidance and leader-follower cooperative guidance.2-4In the aspect of communication topology of multiple missiles,the distributed cooperative guidance method has gradually become the hotspot instead of centralized method5. In order to improve the interception ability and strike ability of multiple missiles,the classification of guidance law is mostly based on cooperative constraints.6For example,for attacking the key parts of the target accurately, the cooperative guidance law is required to hit the target with desired attacking angles for achieving better killing effect7-11; The guidance law for multiple missiles with cooperative attacking time constraint can achieve the effect of salvo attack12-17; In addition, considering the energy and velocity consumption for missiles, Refs. [18-22] studied the optimal cooperative guidance method based on minimum energy consumption.

However, in the above studies of cooperative guidance methods with multiple constraints, the targets considered are mostly stationary targets, uniformly moving targets or targets whose speed and maneuver capability are relatively smaller compared with that of missiles.For the interception of the target with large maneuver and high speed,the above cooperative guidance law7-22under various constraints cannot guarantee that the missiles will not collide before intercepting the target in principle.And it cannot guarantee that the multiple missiles can effectively intercepting the large-maneuver target when the acceleration limit exists. At present, there are few cooperative guidance methods for large maneuver targets. Therefore, it is necessary to explore other feasible and effective cooperative guidance methods to intercept large maneuvering targets.

In Ref. [23], the concept of virtual aiming point is introduced to solve the problem of cooperative interception maneuvering targets, and cooperative guidance problem is transformed into an optimization problem. The guidance law proposed in Ref.[24]adds a bias term calculated from the virtual aiming points on the basis of true proportional guidance law,which achieves that multiple missiles can cover the target’s maneuvering range to the maximum extent.Ref.[24]extended the situation of Ref. [23]to the three-dimensional interception case, and proposed a cooperative guidance strategy based on full coverage. The strategy coordinates the coverage range of different missiles to strike high-speed maneuvering targets. In order to improve the detection accuracy of information sharing among missiles, a cooperative detection framework was proposed in Ref.[25].Based on the above dynamic target coverage theory, the reachable set of missiles was designed to cover the target dynamic area as far as possible to maximize the interception probability. Ref. [26] studied the cooperative interception problem of multiple missiles against highmaneuvering targets. The proposed interception algorithm consists of two parts: the cooperative guidance algorithm to generate the desired position of each interceptor and the optimal control law to drive the interceptor to the desired position with minimum energy. Under certain assumptions, the joint probability of interception is estimated to evaluate the interception performance.

It is worth noting that the above studies rarely took into account the actual overload saturation constraint of the missile, especially when intercepting large maneuvering targets.Besides, Refs. [22-24] proposes a cooperative guidance strategy based on dynamic coverage theory. Under the linearized model, the cooperative interception problem based on biased differential game, biased proportional guidance and threedimensional biased true proportional guidance is studied respectively in Refs.[22-24].The results show that the multiple missiles under the strategy can intercept the target which is higher maneuvering than the missiles. However, in the terminal guidance stage, the target’s large maneuver will increase the nonlinear characteristics in the interception process. In Ref. [27], a cooperative interception strategy based on escape field coverage is proposed under nonlinear interception geometry. Besides, the relationship among the initial array position of terminal guidance, guidance parameters and the coverage area of target maneuver of the missile is studied. However,Ref. [27] only studies on the two-dimensional plane, and the cooperative interception strategy for the nonlinear dynamic model under the three-dimensional case is still open and has great research space and value.

Inspired by the above research status,based on the feasible dynamic coverage theory, this paper studies the problem of cooperative interception of highly maneuverable targets using the three-dimensional nonlinear dynamic guidance model with saturation maneuvering.Compared with the existing results on cooperative interception of large maneuvering targets, the main contributions of this paper are as follows. Firstly, the nonlinear motion model of missile and target is established in three-dimensional plane, while the linear model is used in Refs.[22-24].Secondly,based on the idea that small circle covering large circle,the problem of cooperative covering strategy in three-dimensional space is analyzed and three-dimensional standard trajectory theory is proposed. Thirdly, numerical algorithm of cooperative coverage strategy is given to solve the minimum number of missiles and initial array position with known missile and target reachable area, while the Refs. [26]cannot obtain the minimum number of missiles and the Ref.[27] just calculate the minimum number of missiles in two dimensions plane. Finally, based on the cooperative coverage strategy, the design method for the cooperative guidance law under three-dimensional plane is proposed and the strategy of dynamic adjustment of guidance parameters is designed.Although the guidance law with acceleration limit were studied in Refs.[17-19],these methods cannot guarantee that the missiles can intercept the target with large maneuver and high speed.

The rest of this paper is organized as follows. In Section2,preliminaries and problem description are given. In Section 3,the cooperative coverage strategy is proposed and the algorithm for cooperative coverage strategy is designed. Section 4 presents the detailed design process of cooperative guidance laws based on cooperative coverage strategy. In Section 5,numerical simulation results for proposed strategy and guidance law are shown, Section 6 summarizes the whole paper.

2. Preliminaries and problem description

2.1. Nonlinear three-dimensional model of cooperative guidance

Assuming that the missile and the target can be regarded as point masses, and the performance of the missile’s attitude dynamics is not considered in this paper. The threedimensional guidance model of the multiple missiles against the target is shown in Fig. 1.

Fig. 1 Three-dimensional guidance model.

where Miis the ith missile, V is velocity, θ And φ are ballistic deflection angle and ballistic inclination angle, respectively. θq，iis the angle between the projection of the Line of Sight (LOS) on the xoy plane and the x-axis. φq，iis the angle between the LOS and the xoy plane. The three-dimensional nonlinear guidance model can be decomposed into two planes:one is the longitudinal plane containing the LOS and perpendicular to the z axis, the other is the lateral plane-xoy.The relative motion equation on the longitudinal plane can be written as:

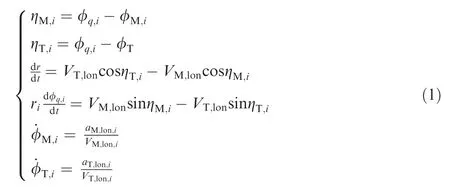
where η is the velocity leading angle on the longitudinal plane.alonis longitudinal acceleration.Vlonis the velocity component in the longitudinal plane, which is defined as:

where σ is the velocity leading angle on the lateral plane. The relative motion equation on the lateral plane can be written as:

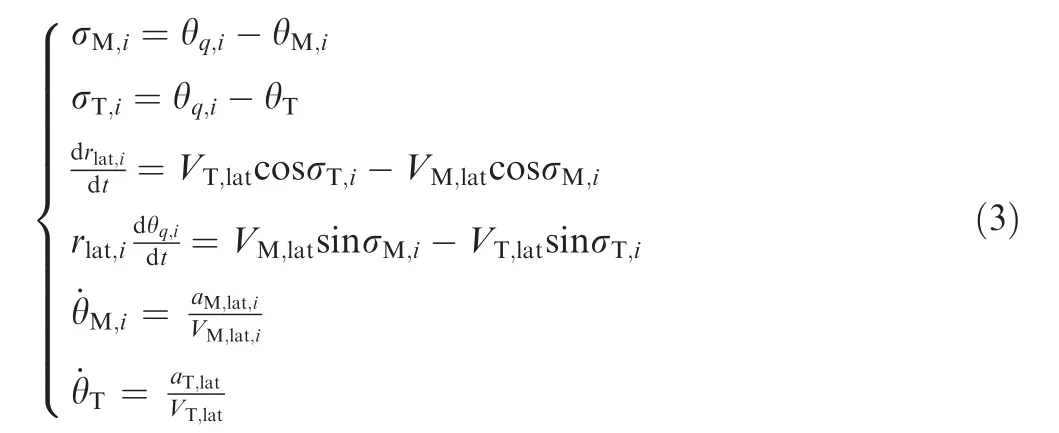
where alatis lateral acceleration.Vlatis the velocity component in the lateral plane. rlat，iis the projection of the distance between the ith missile and the target on the lateral plane:

2.2. Problem formulation

Definition 1. Cooperative interception is defined as at least one missile in the multiple missiles successfully intercepts the target and the acceleration of missile does not exceed its upper limit during the guidance process.

In the process of intercepting the target,in the case that the acceleration of the missile is not saturated,each missile has an attack area, denoted as AF. This area is determined by the velocity, initial position, acceleration limitation and guidance law of the missile, and it is the maximum area that the missile can reach under the condition of specific guidance law and overload unsaturation. In addition, there is also a maximum escape area for the maneuvering target, that is, the area that can be reached when the target moves with the maximum acceleration, which can be denoted as AE. In order to make the multiple missiles successfully intercept the target with higher maneuverability,it is required that the union of the attack area of the multiple missiles is greater than the maximum escape area of the target, that is, (AF1∪AF2···∪AF3)⊇AE.

For the convenience of calculation and derivation, the three-dimensional reachable area can be represented in the two-dimensional coordinate system composed of the lateral acceleration and the longitudinal acceleration defined in the Section 2.1, as shown in Fig. 2. where aT，maxis the maximum acceleration of the target. Thus, the reachable area AEof the target is a circle with radius aT，max. aM，maxis the maximum acceleration of the missile, and a～M，maxis the acceleration required for the missile to reach the boundary of the attack area AF, which is called coverage acceleration. And the target reachable area is the large circle and the missile attack area is the small circle. Because of the effect of acceleration saturation, one can obtain that a～M，max＜aM，max. Therefore, as for the problem of effectively cooperative intercepting on the target with higher maneuverability,this paper proposes a cooperative coverage strategy and the cooperative guidance law according to relationship of the maximum maneuver capability of the missile and the target.

Fig. 2 Reachable area of missile and target.

3. Cooperative coverage strategy

According to the cooperative interception method in section 2,the problem of cooperative coverage strategy can be transformed into the related problem of‘‘small circle covering large circle”. Some related studies have been done in Refs. [28-30].According to the radius of the large circle and the number of small circles, the minimum radius of the small circle is calculated. However, with the increase of the number of small circles, most of the results in Refs. [28-30] are obtained based on computer experiments. The calculation of the position of small circles is complicated and difficult to be solved quickly.Moreover,the number of small circles in the experimental data is limited. The cooperative coverage strategy in this paper is expected to quickly obtain the minimum number of small circles and the center position of small circles for any given large circle radius (aT，max) and small circle radius ().

Assumption 1.The large circle is the unit circle and the radius of the small circle is μ, and the radius of the small circle is restrained as μ =/aT，max∈ (1/3，1).

Remark 1.Assumption 1 is a mild and reasonable assumption.The interception process which the coverage acceleration of the missile is less than the maximum acceleration of the target is studied in this paper. And the smaller the coverage acceleration of the missile, the larger the number of missiles required, which tends to rise exponentially, and the calculation of the minimum number of missiles becomes more complex.22-24Thus,μ ∈ (1/3，1) is reasonable.

According to μ,the steps of the cooperative coverage strategy are as follows.The specific solving steps of Step 2 in Algorithm 1 are as follows:

Algorithm 1. Algorithm for implement cooperative coverage strategy Step 1. Input missile coverage acceleration a～M，max and target maximum acceleration aT，max.Then,the radius of small circle can be obtained, that is, μ = a～M，max/aT，max Step 2. If μ ∈ ■■■■2/2，1（ ）, one can cover the whole large circle by making the diameter of the small circle as the chord length of the large circle.Thus,the small circle covers the circumference of the large circle that is, the boundary of the large circle. Otherwise proceed to Step 3.Step 3. If μ ∈ 0.577，■■■2■/2）, one can determine the number of small circles by making the center of the large circle on the boundary of the small circle, as shown in Fig. 3(a). Otherwise proceed to Step 4.Step 4.If μ ∈ 1/3，0.577（( ),in order to achieve complete coverage of the center region,a small circle is fixed in the center of the large circle, called as Center Small Circle (CSC). And the rest of the small circle called as Outer Small Circle(OSC),as shown in Fig.3(b).Step 5. Output the minimum number n of small circles required and the center position OMn of each small circle, where Mn=1,2,...,n.

Fig. 3 Geometric sketch of cooperative coverage strategy.

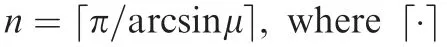
The specific solving steps of Step 4 in Algorithm 1 are as follows:

In order to make that the whole large circle is completely covered, the OSC should cover the circumference of the CSC in addition to the circumference of the large circle. According to the geometric relation, the following equations can be obtained:

where n1is the number of OSC needed to cover the circumference of CSC.

When μ ≤1/3, the method of Step 4 cannot completely cover the area of the large circle, which will not be discussed here.

Remark 2.The boundary values of Step 3 and Step 4 in Algorithm 1 are 0.577 according to the simulation results.That is, the method in Step 3 is used to calculate in a between 0.5 and, and the method in Step 4 is used to calculate in a between 0.3 and, and the optimal boundary value is finally obtained.

4. Cooperative guidance law based on coverage strategy

4.1. Design of cooperative guidance law

According to the cooperative coverage strategy in Section 2,it is necessary to calculate the coverage acceleration (a～M，max) of the missile in order to completely cover the entire escape area of the target.a～M，maxis mainly determined by the speed and the maximum overload of the missile and the guidance law characteristics. The missile’s velocity and overload are restricted by the missile type and can be dealt with as a precondition, and the characteristics of guidance law are studied in this paper.By designing a reasonable guidance law, the attack area of a single missile is made as large as possible.That is,the coverage acceleration of the missile is as close as possible to the maximum acceleration of the missile,so as to ensure that each missile plays the maximum combat value.

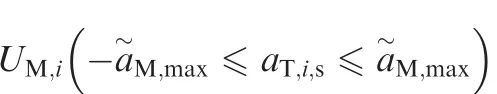
Based on the Three-dimensional guidance model,the longitudinal acceleration and lateral acceleration of the Miin the longitudinal plane and the lateral plane can be designed respectively. The form of guidance law is as follows:

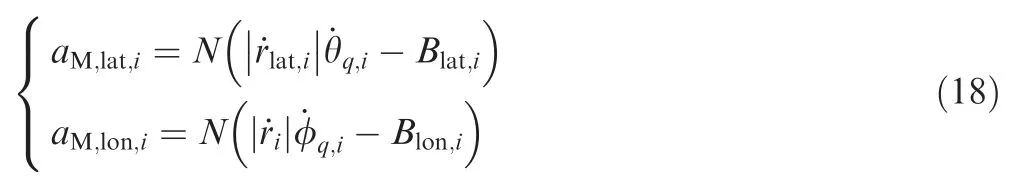
where N is the navigation ratio.aM，lon，iis the cooperative guidance law in the longitudinal plane and aM，lat，iis the cooperative guidance law in the lateral plane. Blat，iis the cooperative bias term in the lateral plane and Blon，iis the cooperative bias term in the longitudinal plane.

From Eq. (18), one can see that the cooperative guidance law is composed of proportional guidance and cooperative bias, in which the proportional guidance is used for interception of non-standard trajectory and the cooperative bias is used for interception of standard trajectory. Assuming that the velocity of missile and the target remain unchanged, the derivative of the fourth equation in Eq. (1) can be obtained:

In order to minimize the acceleration of the Miwhen intercepting the target with the standard trajectory, the overload of the entire interception process can be reduced by minimizing the overload of the initial moment and the intercepting point:

When the Miintercepts the maneuvering target with the acceleration of aT，i，sbased on the standard trajectory, the target acceleration can also be decomposed into the lateral plane and the longitudinal plane.According to Eq.(18)and(23),one has

Then,the bias term in the guidance law can be obtained by sorting out Eq. (25):

According to Eq.(26),the bias term is related to the target’s leading angle and target’s acceleration at the interception moment.

Theorem 1.When the cooperative guidance law is in the form of Eq. (18), multiple missiles can achieve cooperative interception of the target according to the coverage strategy.And this design technique can ensure that when the missile intercepts the target with a standard trajectory, the acceleration at the intercepting point is zero.

Proof.For the entire attack area of Mi, the missile’s acceleration at the initial moment should be minimized. Therefore,according to Eqs.(1),(2),(18)and(23),missile i should satisfy the following equation at the initial moment:

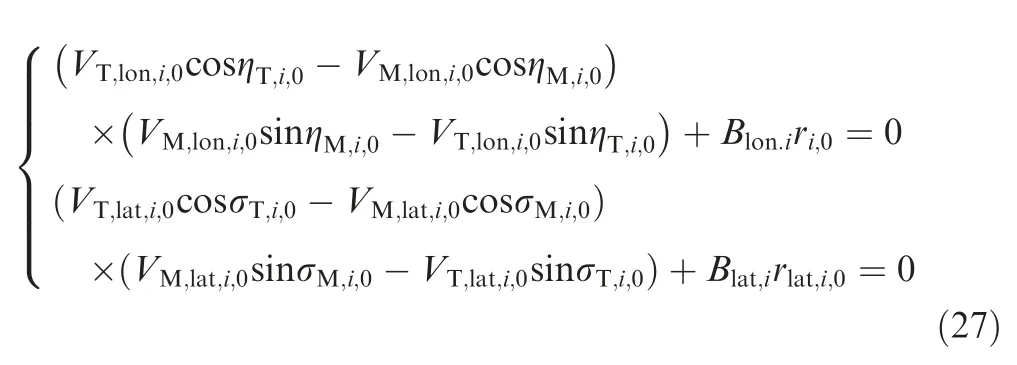
Since ˙φq，iand ˙θq，iare finite values and ri，f=0,rlat，i，f=0,combining Eqs. (1) and (2), it can be obtained that the missile should meet the following equation at the intercepting point:

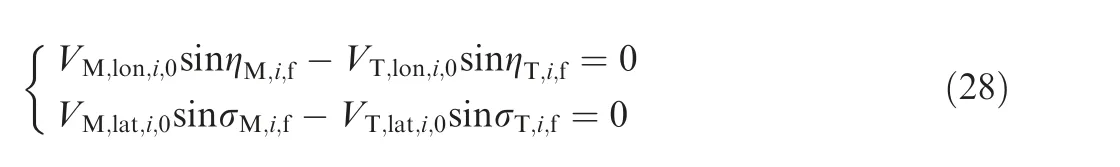
When the missile intercepts the target with the standard trajectory, the change of ˙r and ˙rlatis not big, so they can be considered as constant.The range rate at the initial moment(˙ri，0，s)can be used to replace the range rate in the interception process(˙ri，s(t )).Similarly, ˙rlat，i，0，scan be used to replace ˙rlat，i，s(t ),and the acceleration of the target is assumed to be unchanged. In addition, the velocity component of the missile in the two planes does not change much,which can be regarded as a constant,and is also replaced by the velocity component at the initial moment, that is, VM，lon，i，s= VMcosσM，i，0，s, VT，lon，i，s=VTcosσT，i，0，s, VM，lat，i，s= VMcosφM，i，0，s,VT，lat，i，s=VTcosφT，0，s.Then the time-to-go of missile i can be approximated as

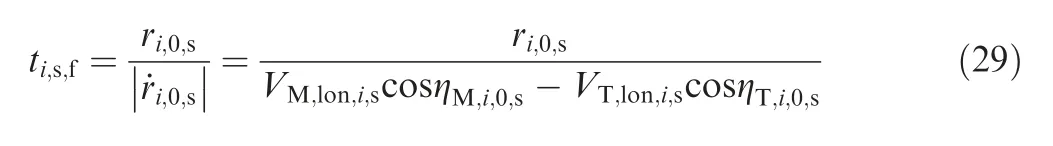
Then take the derivative of the first equation and combine it with the fifth equation in Eq. (1) to get the following equation:

Take the derivative of the second equation and combine it with the sixth equation in Eq. (1) to get the following equation:

Combining Eqs. (18) and (30), one gets

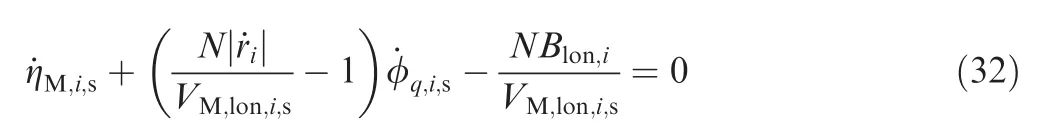
By combining Eqs.(31)and(32), ˙φq，i，scan be eliminated by

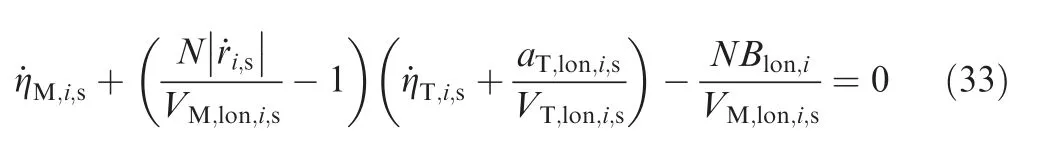
The following equation can be obtained by integrating Eq.(33):

Similarly,the relationship of leading angle between the initial moment and the intercepting point in the lateral plane can be expressed as

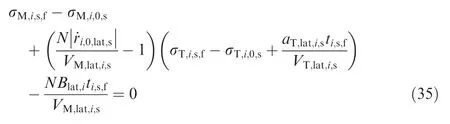
To sum up,Eqs.(27),(28),(34)and(35)constrain the relationship between the leading angles of the missile and the target at the initial moment and the point of impact when intercepting with a standard trajectory. Therefore, combining Eq. (23), the above constraints could be written as

Given the transition condition of the mid-terminal guidance of the missile,the initial array position and cooperative bias of the missile corresponding to the target escaping with acceleration aT，i，s，lonand aT，i，s，latcan be quickly solved according to Eq.(36).According to the cooperative coverage strategy in the previous section,the standard trajectory is the acceleration corresponding to the center of the small circle. Thus, according to the obtained initial array position and cooperative bias,multiple missiles can achieve cooperative interception of target under the proposed cooperative guidance law. And when the missile intercepts the target with a standard trajectory, the acceleration at the intercepting point is zero. The proof for Theorem 1 is completed.

When the equal sign is taken from the Eq. (37), the maximum longitudinal acceleration aT，lon，i，maxof the missile i to intercept the target in the longitudinal plane can be obtained.Besides, one has a～

M，i，max = aT，lon，i，max.

Similarly, when the equal sign of the following equation is taken,the coverage acceleration of the missile can be obtained in the horizontal plane.Then,one has= aT，lat，i，max,and

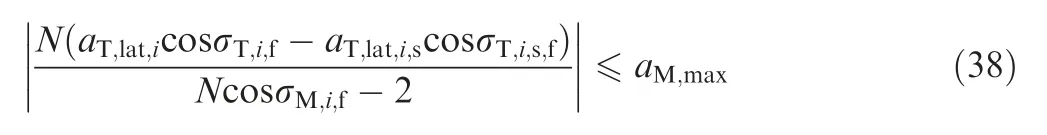
4.2. Dynamic adjustment strategy

In the above derivation, some mathematical simplifications were made for the sake of computational convenience, including that the maneuverability of the target is constant. However, in the actual cooperative interception process, the target’s acceleration is likely to be constantly changing. Thus,when the target is in some escape mode of extraordinary maneuvers, the cooperative interception will fail of the multiple missiles, that is, no missile intercepts the target. In addition, due to the inevitable errors in angle or position during the shift of mid-terminal guidance, the multiple missiles may not really cover the target’s maneuver area. Therefore, it is very necessary for the multiple missiles to adjust the guidance parameter Biin real time to overcome the above problem.

Based on the relative distance between the missile and the target at each moment, a missile with the best interception effect at the current moment can be found. The cooperative offset term of the missile with the shortest distance between the missile and the target is taken as the optimal cooperative offset term Bbest(t ) at the current moment, and then Bi(t+1)at the next moment can be calculated according to the following equation:

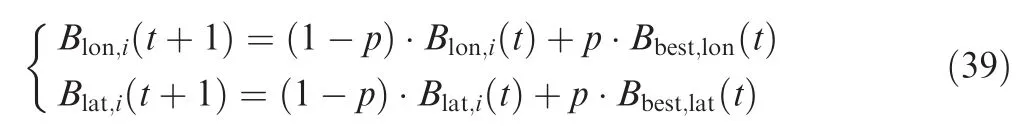
where p is the weight factor (0 ＜p ≤1), which is designed to prevent the change of the cooperative offset term of the missile from being too drastic. When the target maneuvers with the constant value aT，i，scorresponding to the standard trajectory,the cooperative bias term of the Miis always the initial value.Thus,the flow diagram of cooperative guidance based on coverage strategy is shown in Fig. 4.

5. Simulation and analysis

The missiles are assumed have the speed of 7 Ma and the maximum maneuvering acceleration of 3.5 g. The target’s speed is 6 Ma and the maximum maneuvering acceleration is 4 g. The initial distance between the missile and the target is 50 km and the navigation ratio N is 4.The multiple missiles enter terminal guidance at the same time and the initial velocity direction point to the target.According to the cooperative coverage strategy algorithm in section three, the number of missiles needed to intercept the target is 9, denoted as M1-M9.

Fig.5 is the schematic diagram of the obtained cooperative coverage strategy. Where, each small circle represents the cooperative coverage area of each missile, and the radius μ of the small circle is 0.4363. Thus, the coverage acceleration of each missile is a～M，max= μ·aT，max=1.7452g. It can be seen that under the limitation of the traditional proportional guidance law, the cover acceleration of the missile is only about half of the maximum usable overload of the missile. The position of the center of each small circle multiplied by the maximum acceleration of the target is the acceleration corresponding to the standard trajectory. For example, the center of M1is (0.57, 0.57), then the standard trajectory of M1is (2.28,2.28)g. In addition, the information of each missile’s cooperative bias and target leading angle obtained by the cooperative coverage algorithm is shown in Table 1.

Using the initial information obtained by the cooperative coverage strategy, the hypothesis of the standard trajectory is verified below. Taking the standard trajectory of M1as an example,when the target is maneuvering with the lateral acceleration of 22.3671 and the longitudinal acceleration of 22.6371, the ballistic and overload curve of M1are shown in Fig. 6.

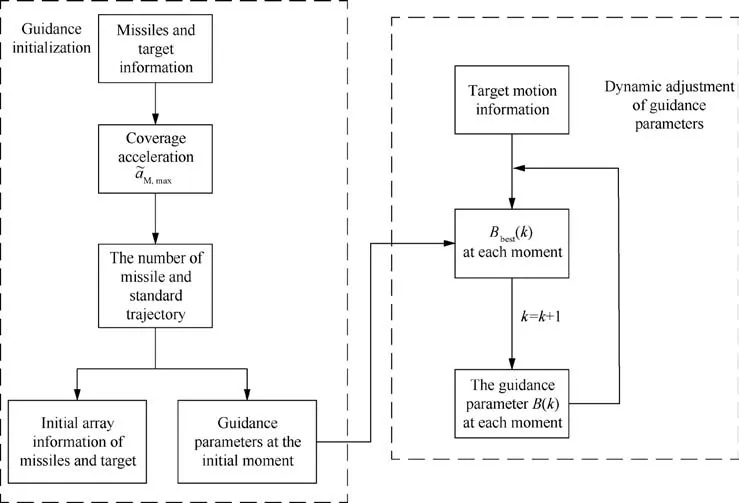
Fig. 4 The flow diagram of cooperative guidance based on coverage strategy.

Fig. 5 Schematic diagram of the obtained cooperative coverage strategy.

As seen in Fig.6,the trajectory of missile 1 is very straight,and the ratio of the actual overload used to the maximum overload is within 11×10-3. That is, the required overload during the entire interception process is very small, consistent with the assumptions of the standard trajectory in Section 4.

The following figure is a comparison of the interception effects of the cooperative guidance law based on coverage strategy and the proportional guidance law. Both of the two guidance laws are simulated with the initial interception array in Table 1,respectively.And the minimum miss distance in the missile group is recorded as the miss distance of the cooperative interception. Target maneuvers vary from 0 to max. The distribution of miss distance of the cooperative guidance law based on coverage strategy and proportional guidance law with respect to the target maneuver is shown in Fig. 7.

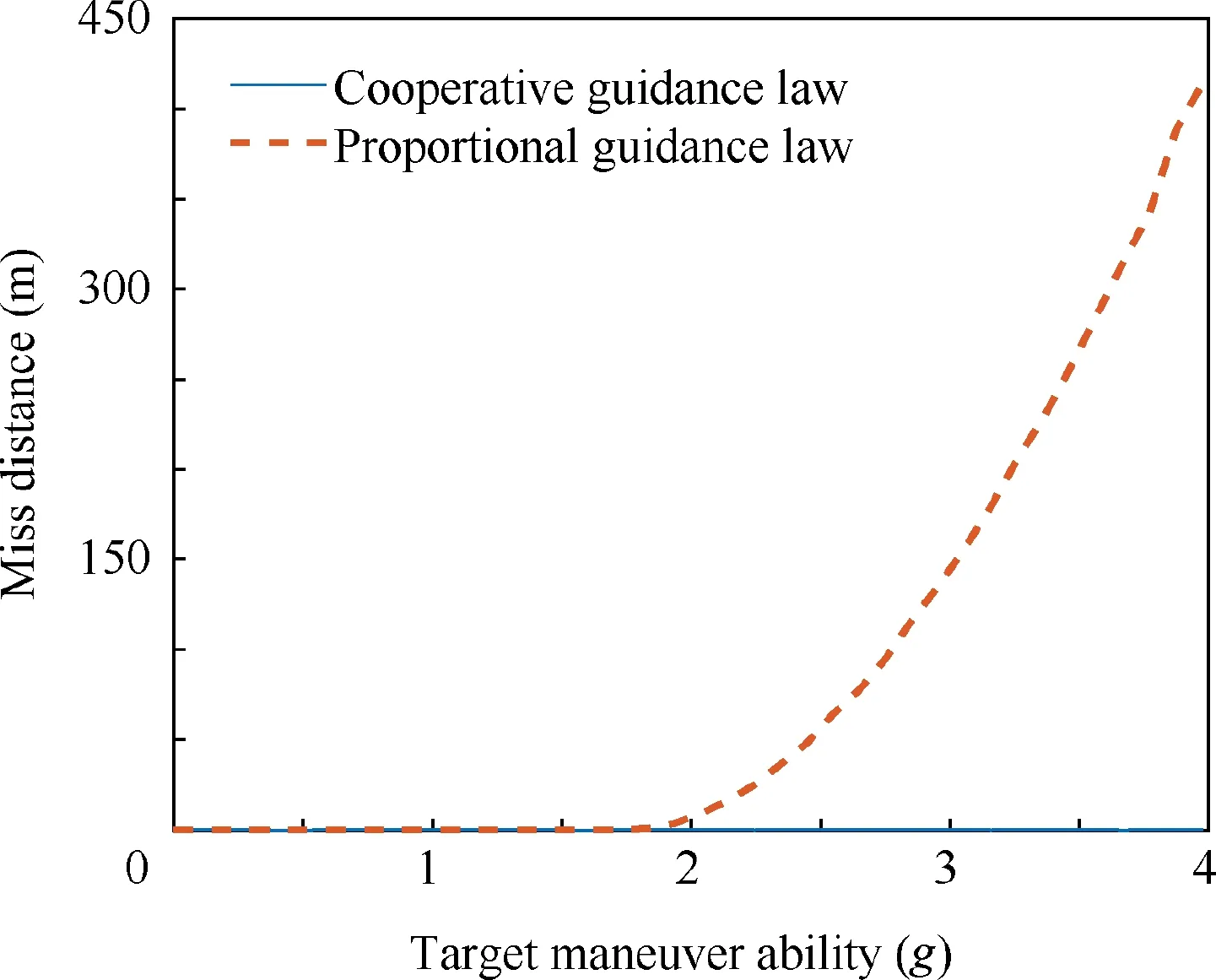
Fig. 7 Distribution of miss distance

It can be seen from Fig. 7 that when the target’s maneuver ability is less than about 1.75 g, there is almost no difference between proportional guidance and cover-based cooperative guidance, and the miss distance is almost 0. However, with the improvement of target maneuver ability, the miss range of proportional guidance gradually increases. When the target maneuver size is about 1.85 g, the multiple missiles cannot intercept the target under proportional guidance. When the target is maneuvering with maximum overload,the miss range of the missile group under proportional guidance law is as high as 400 m.

Table 1 Solution results of cooperative coverage strategy.

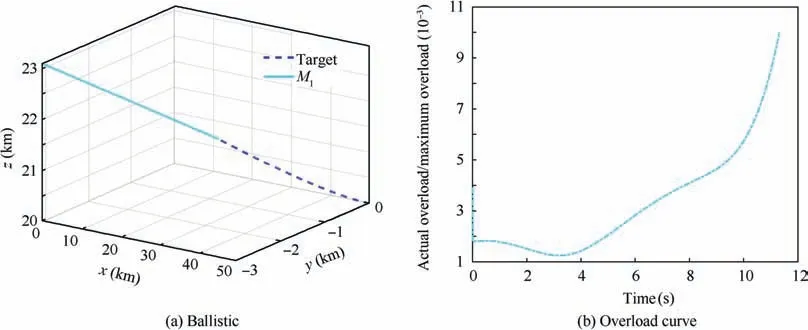
Fig. 6 Ballistic and overload curve of M1

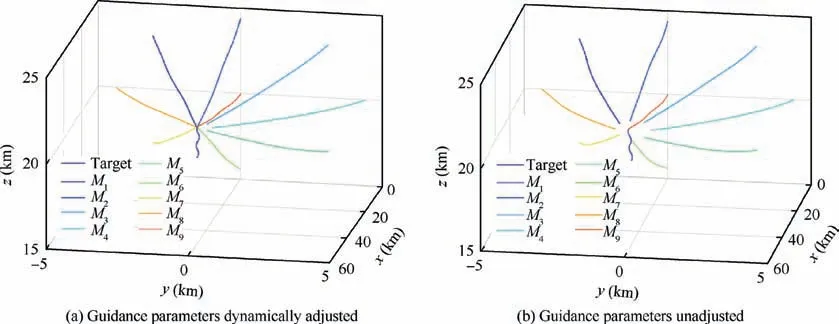
Fig. 8 Guidance parameters dynamical adjustment strategy

The simulation results above verify the effectiveness of the cooperative guidance law under constant target maneuver.The following simulation compares the interception effect of guidance parameters without dynamic adjustment and dynamic adjustment in the case of target changing maneuver.Suppose the target does a square wave maneuver aT=aT，maxsign(s in(πt/3)). Fig. 8 shows the cooperative interception trajectory with guidance parameters dynamically adjusted and unadjusted.

As can be seen from Fig. 8, the trajectory after dynamic adjustment of guidance parameters is straighter. And the miss distance of multiple missiles is smaller, which improves the effect of overall cooperative interception.Thus,the above simulation results verify the effectiveness of dynamic adjustment strategy in Section 4.

6. Conclusions

The problem of multiple missiles with weak maneuverability intercept a target with strong maneuverability was studied. A cooperative coverage strategy based on large circle covering small circle is proposed for three-dimensional nonlinear model.The relationship between the initial array position, guidance law parameters and the coverage area of the missile to the maneuvering target is discussed. Then, based on cooperative interception strategy and the concept of standard trajectory,a cooperative guidance law based on coverage strategy is designed. In addition, a method of dynamic adjustment of guidance parameters is proposed to reduce cooperative guidance error. Finally, the simulation results prove the effectiveness of the proposed cooperative coverage strategy and cooperative guidance law.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the Science and Technology Innovation 2030-Key Project of‘‘New Generation Artificial Intelligence”, China (No.2020AAA0108204), the National Natural Science Foundation of China (Nos.61922008, 61973013,61873011,61803014), the Innovation Zone Project, China(No.18-163-00-TS-001-001-34), the Defense Industrial Technology Development Program, China (No.JCKY2019601C106), the Beijing Natural Science Foundation(No. 4182035, the Special Research Project of Chinese Civil Aircraft,China National Postdoctoral Program for Innovative Talents(No.BX20200034),and Project funded by China Postdoctoral Science Foundation(No.2020 M680297).